DOCSLIB.ORG

A Statistical Application in Astronomy: Streaming Motion in Leo I

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Statistical Application in Astronomy: Streaming Motion in Leo I Streaming motion in Leo I Separating signal from background A statistical application in astronomy: Streaming motion in Leo I Bodhisattva Sen DPMMS, University of Cambridge, UK Columbia University, New York, USA [email protected] ETH Zurich, Switzerland 31 May, 2012 Streaming motion in Leo I Separating signal from background Outline 1 Streaming motion in Leo I Modeling Threshold models 2 Separating signal from background Method Theory Streaming motion in Leo I Modeling Separating signal from background Threshold models What is streaming motion? Local Group dwarf spheroidal (dSph) galaxies: small, dim Is Leo I in equilibrium or tidally disrupted by Milky Way? Such a disruption can give rise to streaming motion: the leading and trailing stars move away from the center of the main body of the perturbed system Streaming motion in Leo I Modeling Separating signal from background Threshold models Data on 328 stars (Y ; Σ): Line of sight velocity; std. dev. of meas. error (R; Θ): Projected position, orthogonal to line of sight Contaminated with foreground stars (in the line of sight) Magnitude of streaming motion Likely to increase beyond a threshold radius Likely to be aligned with the major axis of the system Streaming motion in Leo I Modeling Separating signal from background Threshold models Statistical questions Is streaming motion evident in Leo I? If so, how can it be described and estimated? To what extent can it be described by a threshold model? Findings [Sen et al. (AoAS, 2009)]: The magnitude of streaming motion appears to be modest, (nearly) significant at 5% level Appears consistent with a threshold model Difficult to identify the threshold radius precisely Streaming motion in Leo I Modeling Separating signal from background Threshold models Outline 1 Streaming motion in Leo I Modeling Threshold models 2 Separating signal from background Method Theory Streaming motion in Leo I Modeling Separating signal from background Threshold models 2 Yi = ν(Ri ; Θi ) + i + δi ; i ∼ N(0; σ ) independent of (R; Θ) 2 Measurement error: δi jΣi ∼ N(0; Σi ) Cosine Model: ν(r; θ) = ν + λ(r) cos θ; λ " n 2 X fYi − v − u(Ri ) cos Θi g (ν; ^ λ^ ) = arg min v2 ;u" σ2 + Σ2 R i=1 i 1 n 2 X ^ 2 2 σ^ = [fYi − ν^ − λ(Ri ) cos Θi g − Σi ] n i=1 λ measures the effect of streaming; λ " cos θ determines the deviation from the major axis Streaming motion in Leo I Modeling Separating signal from background Threshold models λ^ Simulated effect of streaming Streaming motion in Leo I Modeling Separating signal from background Threshold models Is streaming evident? Test λ = 0 using log-likelihood ratio statistic No streaming: ν(r; θ) ≡ ν, a constant P-value ≈ 0:055 (using permutation test) How much is streaming at radius r? Need point-wise confidence intervals for λ d Result: n1=3fλ^(r) − λ(r)g ! ηC. Need to estimate η – tricky! Need ways to by-pass the estimation of η. Likelihood ratio (LR) based test or bootstrap methods LR is pivotal and can be used to construct CI for λ(r) (Banerjee and Wellner, AoS, 2001) Streaming motion in Leo I Modeling Separating signal from background Threshold models Likelihood ratio based method Banerjee and Wellner, AoS, 2001 Test H0 : λ(r) = ξ0 n 2 n 2 X fYi − v − u(Ri ) cos Θi g X fYi − v − u(Ri ) cos Θi g ∆SSE(r; ξ0) = min − min v2 ;u(r)=ξ ;u" σ2 + Σ2 v2 ;u" σ2 + Σ2 R 0 i=1 i R i=1 i d Under H0, ∆SSE(r; ξ0) ! D D does not contain any nuisance parameters Invert this sequence of hypotheses tests (by varying ξ0) to get a CI for λ(r) Streaming motion in Leo I Modeling Separating signal from background Threshold models Bootstrap methods Want to bootstrap n1=3fλ^(r) − λ(r)g Efron’s bootstrap fails We claim that the bootstrap estimate does not have any weak limit (Sen et al., AoS, 2010) Smoothed bootstrap works LR Bootstrap 0.90 0.95 0.90 0.95 ^ r0 L U CP L U CP L U L U λ 400 0 3.54 .901 0 3.86 .952 0 3.57 0 3.57 1.92 500 0.10 4.50 .882 0 5.02 .936 0 3.58 0 3.90 1.98 600 0.26 6.66 .827 0 7.30 .897 0 3.30 0 3.64 1.98 700 0.36 8.88 .913 0.05 9.56 .961 0 4.26 0 4.69 1.99 750 1.85 8.88 .906 1.37 9.56 .952 0.44 7.86 0 8.37 5.37 Streaming motion in Leo I Modeling Separating signal from background Threshold models Outline 1 Streaming motion in Leo I Modeling Threshold models 2 Separating signal from background Method Theory Streaming motion in Leo I Modeling Separating signal from background Threshold models Threshold models Goal: To determine a “threshold” in the domain of the function where some “activity” takes place Could either be a rapid change in the function value or a discontinuity Find the threshold radius in the Leo I ( 0 0 ≤ r ≤ d ; Model: ν(r; θ) = ν + λ(r) cos θ where λ(r) = 0 > 0 d0 < r ≤ 1: Two approaches: change point versus split point Streaming motion in Leo I Modeling Separating signal from background Threshold models Change point models ν(r; θ) = ν + β (r − ρ) cos θ 1.0 1.0 0.8 0.8 0.6 0.6 0.4 0.4 0.2 0.2 0.0 0.0 -1.0 -0.5 0.0 0.5 1.0 -1.0 -0.5 0.0 0.5 1.0 x x (x) = 1fx ≥ 0g (x) = max(0; x) Streaming motion in Leo I Modeling Separating signal from background Threshold models Change point models ν(r; θ) = ν + β (r − ρ) cos θ ρ is the change-point 2 Pn fYi −v−β (Ri −r) cos Θi g Minimize: SSE(v; β; r) = i=1 2 2 σ^ +Σi SSE(v^; β;^ r) − SSE(v^; β;^ ^r) Streaming motion in Leo I Modeling Separating signal from background Threshold models Split point model Do not assume specific form for λ(r); λ " Find the closest stump to λ (under mis-specification) R r 2 R τ 2 κ(b; r) = 0 λ (s)ds + r [λ(s) − b] ds Population parameters: (β; γ) = arg min κ(b; r) γ is the split point Estimate λ by λ^ to estimate γ Streaming motion in Leo I Modeling Separating signal from background Threshold models Rescaled version of the criterion function Asymptotics for the split point: n1=3-rate of convergence? Streaming motion in Leo I Method Separating signal from background Theory Outline 1 Streaming motion in Leo I Modeling Threshold models 2 Separating signal from background Method Theory Streaming motion in Leo I Method Separating signal from background Theory Problem Most astronomical data sets are polluted to some extent by foreground/background objects (“contaminants/noise”) that can be difficult to distinguish from objects of interest (“member/signal”) Contaminants may have the same apparent magnitudes, colors, and even velocities as signal stars How do you separate out the “signal” stars? We develop an algorithm for evaluating membership (estimating parameters & probability of an object belonging to the signal population) Streaming motion in Leo I Method Separating signal from background Theory Example Data on stars in nearby dwarf spheroidal (dSph) galaxies Data: (X1i ; X2i ; V3i ; σi ; ΣMgi ; :::) Velocity samples suffer from contamination by foreground Milky Way stars Streaming motion in Leo I Method Separating signal from background Theory Approach Our method is based on the Expectation-Maximization (EM) algorithm We assign parametric distributions to the observables; derived from the underlying physics in most cases The EM algorithm provides estimates of the unknown parameters (mean velocity, velocity dispersion, etc.) Also, probability of each star belonging to the signal population; see Walker et al. (2008) Streaming motion in Leo I Method Separating signal from background Theory Streaming motion in Leo I Method Separating signal from background Theory A toy example Suppose N ∼ Poisson(b + s) is the number of stars observed s = rate for observing a signal star b = the foreground rate Given N = n, we have W1;:::; Wn ∼ fb;s where data n bfb(w)+sfs(w) fWi = (X1i ; X2i ; V3i ; σi )gi=1, and fb;s(w) = b+s We assume that fb and fs are parameterized (modeled by the underlying physics) probability densities Streaming motion in Leo I Method Separating signal from background Theory For galaxy stars The stellar density (number of stars per unit area) falls exponentially with radius, R The distribution of velocity given position is assumed to be 2 2 normal with mean µ and variance σ + σi For foreground stars The density is uniform over the field of view The distribution of velocities V3i is independent of position (X1i ; X2i ) We adopt V3i from the Besancon´ Milky Way model (Robin et al. 2003), which specifies velocity distributions of Milky Way stars along a given line of sight Streaming motion in Leo I Method Separating signal from background Theory Outline 1 Streaming motion in Leo I Modeling Threshold models 2 Separating signal from background Method Theory Streaming motion in Leo I Method Separating signal from background Theory Model Suppose N ∼ Poisson(b + s) is the number of stars observed s = rate for observing a signal star b = the foreground rate Given N = n, we have W1;:::; Wn ∼ fb;s where data n bfb(w)+sfs(w) fWi = (X1i ; X2i ; V3i ; σi ; ΣMgi ;:::)gi=1, and fb;s(w) = b+s We assume that fb and fs are parameterized (modeled by the underlying physics) probability densities; β = (s; b; µ, σ2;:::) We would ideally like to maximize the likelihood N Y bfb(Wi ) + sfs(Wi ) L(β) = (Difficult!) b + s i=1 Streaming motion in Leo I Method Separating signal from background Theory The Likelihood Let Yi be the indicator of a foreground star, i.e., Yi = 1 if the i’th star is a foreground star, and Yi = 0 otherwise b Note that Yi ’s are i.i.d.
Load more

Recommended publications
  • Aquarius Aries Pisces Taurus
    Zodiac Constellation Cards Aquarius Pisces January 21 – February 20 – February 19 March 20 Aries Taurus March 21 – April 21 – April 20 May 21 Zodiac Constellation Cards Gemini Cancer May 22 – June 22 – June 21 July 22 Leo Virgo July 23 – August 23 – August 22 September 23 Zodiac Constellation Cards Libra Scorpio September 24 – October 23 – October 22 November 22 Sagittarius Capricorn November 23 – December 23 – December 22 January 20 Zodiac Constellations There are 12 zodiac constellations that form a belt around the earth. This belt is considered special because it is where the sun, the moon, and the planets all move. The word zodiac means “circle of figures” or “circle of life”. As the earth revolves around the sun, different parts of the sky become visible. Each month, one of the 12 constellations show up above the horizon in the east and disappears below the horizon in the west. If you are born under a particular sign, the constellation it is named for can’t be seen at night. Instead, the sun is passing through it around that time of year making it a daytime constellation that you can’t see! Aquarius Aries Cancer Capricorn Gemini Leo January 21 – March 21 – June 22 – December 23 – May 22 – July 23 – February 19 April 20 July 22 January 20 June 21 August 22 Libra Pisces Sagittarius Scorpio Taurus Virgo September 24 – February 20 – November 23 – October 23 – April 21 – August 23 – October 22 March 20 December 22 November 22 May 21 September 23 1. Why is the belt that the constellations form around the earth special? 2.
    [Show full text]
  • Newpointe-Catalog
    NewPointe® Constellation Collections More value from Batesville Constellation Collections 18 Gauge Steel Caskets Leo Collection Leo Brushed Black Silver velvet interior Leo Brushed Black shown with Praying Hands decorative kit. 257178 - half couch Choose from 11 designs. 262411 - full couch See page 15 for your options. • Includes decorative kit option for lid Leo Painted Silver Silver velvet interior 257172 - half couch 262415 - full couch • Includes decorative kit option for lid Leo Brushed Ruby Leo Brushed Blue Leo Painted Sand Leo Painted White Moss Pink velvet interior Light Blue velvet interior Champagne velvet interior Moss Pink velvet interior 257177 - half couch 257179 - half couch 257173 - half couch 257166 - half couch 262410 - full couch 262412 - full couch 262416 - full couch 262414 - full couch • Includes decorative kit option • Includes decorative kit option • Includes decorative kit option • Includes decorative kit option for lid for lid for lid for lid 2 All caskets not available in all locations. Please check to ensure availability in your area. 18 Gauge Steel Caskets Virgo Collection Virgo White/Pink Moss Pink crepe interior| $845 250673 - half couch Virgo White/Pink shown with Roses 254258 - full couch decorative kit and corner decals. Choose from 11 designs. • Includes decorative kit option See page 15 for your options. for lid and corner decals Virgo Blue Light Blue crepe interior 250658 - half couch 254255 - full couch • Includes decorative kit option for lid and corner decals Virgo Silver Virgo White Virgo Copper
    [Show full text]
  • Numerical Solution of Ordinary Differential Equations
    NUMERICAL SOLUTION OF ORDINARY DIFFERENTIAL EQUATIONS Kendall Atkinson, Weimin Han, David Stewart University of Iowa Iowa City, Iowa A JOHN WILEY & SONS, INC., PUBLICATION Copyright c 2009 by John Wiley & Sons, Inc. All rights reserved. Published by John Wiley & Sons, Inc., Hoboken, New Jersey. Published simultaneously in Canada. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600, or on the web at www.copyright.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008. Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created ore extended by sales representatives or written sales materials. The advice and strategies contained herin may not be suitable for your situation. You should consult with a professional where appropriate. Neither the publisher nor author shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.
    [Show full text]
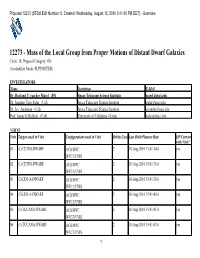
  • 12273 (Stsci Edit Number: 0, Created: Wednesday, August 18, 2010 3:41:48 PM EDT) - Overview
    Proposal 12273 (STScI Edit Number: 0, Created: Wednesday, August 18, 2010 3:41:48 PM EDT) - Overview 12273 - Mass of the Local Group from Proper Motions of Distant Dwarf Galaxies Cycle: 18, Proposal Category: GO (Availability Mode: SUPPORTED) INVESTIGATORS Name Institution E-Mail Dr. Roeland P. van der Marel (PI) Space Telescope Science Institute [email protected] Dr. Sangmo Tony Sohn (CoI) Space Telescope Science Institute [email protected] Dr. Jay Anderson (CoI) Space Telescope Science Institute [email protected] Prof. James S. Bullock (CoI) University of California - Irvine [email protected] VISITS Visit Targets used in Visit Configurations used in Visit Orbits Used Last Orbit Planner Run OP Current with Visit? 01 (1) CETUS-DWARF ACS/WFC 2 18-Aug-2010 15:41:34.0 yes WFC3/UVIS 02 (1) CETUS-DWARF ACS/WFC 2 18-Aug-2010 15:41:36.0 yes WFC3/UVIS 03 (2) LEO-A-DWARF ACS/WFC 2 18-Aug-2010 15:41:38.0 yes WFC3/UVIS 04 (2) LEO-A-DWARF ACS/WFC 2 18-Aug-2010 15:41:40.0 yes WFC3/UVIS 05 (3) TUCANA-DWARF ACS/WFC 2 18-Aug-2010 15:41:41.0 yes WFC3/UVIS 06 (3) TUCANA-DWARF ACS/WFC 2 18-Aug-2010 15:41:43.0 yes WFC3/UVIS 1 Proposal 12273 (STScI Edit Number: 0, Created: Wednesday, August 18, 2010 3:41:48 PM EDT) - Overview Visit Targets used in Visit Configurations used in Visit Orbits Used Last Orbit Planner Run OP Current with Visit? 07 (4) SAGITTARIUS-DWARF- ACS/WFC 2 18-Aug-2010 15:41:44.0 yes IRREGULAR WFC3/UVIS 08 (4) SAGITTARIUS-DWARF- ACS/WFC 2 18-Aug-2010 15:41:46.0 yes IRREGULAR WFC3/UVIS 09 (4) SAGITTARIUS-DWARF- ACS/WFC 2 18-Aug-2010 15:41:47.0 yes IRREGULAR WFC3/UVIS 18 Total Orbits Used ABSTRACT The Local Group and its two dominant spirals, the Milky Way and M31, have become the benchmark for testing many aspects of cosmological and galaxy formation theories, due to many exciting new discoveries in the past decade.
    [Show full text]
  • Astronomy for Kids - Leo
    Astronomy for Kids - Leo The Lion Leo is another companion to Orion in our night sky. You can easily find Leo any Leo Map time that Orion is visible by looking East of the Great Hunter. Although Leo is not as large as Orion, it's distinctive shape makes it very easy to pick out. If you click on the link for the map of Leo on the right, you will notice that the outline of the lion's head and the triangle formed by the stars in the lion's hindquarters are two very distinctive shapes that make this constellation very easy to spot. A map of Leo. Regulus - the Heart of the Lion The largest and brightest star in Leo is Regulus. This large blue star shines brightly as the heart of the lion. Although not a giant star, Regulus is still over five times as large as our Sun. A small telescope will show you that Regulus is part of what is called a "binary system". Binary stars are stars that have one or more companions that orbit around the largest star in the group, much like the planets orbit around our Sun. Find Out More About Leo Chris Dolan's Leo Page Chris Dolan's Leo page has lots of technical information about the stars that make up Leo Richard Dibon-Smith's Leo Page Richard Dibon-Smith's Leo page has a very good explanation of the mythology behind Gemini as well as an excellent reference to its stars and other interesting celestial companions. Original Content Copyright ©2003 Astronomy for Kids Permission is granted for reproduction for non-commercial educational purposes.
    [Show full text]
  • Capricorn (Astrology) - Wikipedia, the Free Encyclopedia
    מַ זַל גְּדִ י http://www.morfix.co.il/en/Capricorn بُ ْر ُج ال َج ْدي http://www.arabdict.com/en/english-arabic/Capricorn برج جدی https://translate.google.com/#auto/fa/Capricorn Αιγόκερως Capricornus - Wikipedia, the free encyclopedia http://en.wikipedia.org/wiki/Capricornus h m s Capricornus Coordinates: 21 00 00 , −20° 00 ′ 00 ″ From Wikipedia, the free encyclopedia Capricornus /ˌkæprɨˈkɔrnəs/ is one of the constellations of the zodiac. Its name is Latin for "horned goat" or Capricornus "goat horn", and it is commonly represented in the form Constellation of a sea-goat: a mythical creature that is half goat, half fish. Its symbol is (Unicode ♑). Capricornus is one of the 88 modern constellations, and was also one of the 48 constellations listed by the 2nd century astronomer Ptolemy. Under its modern boundaries it is bordered by Aquila, Sagittarius, Microscopium, Piscis Austrinus, and Aquarius. The constellation is located in an area of sky called the Sea or the Water, consisting of many water-related constellations such as Aquarius, Pisces and Eridanus. It is the smallest constellation in the zodiac. List of stars in Capricornus Contents Abbreviation Cap Genitive Capricorni 1 Notable features Pronunciation /ˌkæprɨˈkɔrnəs/, genitive 1.1 Deep-sky objects /ˌkæprɨˈkɔrnaɪ/ 1.2 Stars 2 History and mythology Symbolism the Sea Goat 3 Visualizations Right ascension 20 h 06 m 46.4871 s–21 h 59 m 04.8693 s[1] 4 Equivalents Declination −8.4043999°–−27.6914144° [1] 5 Astrology 6 Namesakes Family Zodiac 7 Citations Area 414 sq. deg. (40th) 8 See also Main stars 9, 13,23 9 External links Bayer/Flamsteed 49 stars Notable features Stars with 5 planets Deep-sky objects Stars brighter 1 than 3.00 m Several galaxies and star clusters are contained within Stars within 3 Capricornus.
    [Show full text]
  • From Our Perspective... the Ecliptic
    2/9/09 Why don’t we see the same Mastering Astronomy Assignment 3 constellations throughout the year? • Due Feb 17, 11 am • Read Sections 2.1, 2.2 and S1.2 The Earth also revolves around the Sun, From our perspective... which changes our view of the stars March September Earth circles the Sun in 365.25 days and, The Ecliptic consequently, the Sun appears to go once around the ecliptic in the same period. If we could see • As the Earth orbits background stars in the daytime, our Sun would the Sun, the Sun appears to move a) appear to move against them at a rate of 360° per eastward among the day. stars following a path b) appear to move against them at a rate of about called the ecliptic 15° per day. • The ecliptic is a c) appear to move against them at a rate of about 1° projection of Earth’s per day. orbit onto the The tilt of the Earth's axis d) remain stationary against these stars. celestial sphere causes the ecliptic to be tilted to the celestial equator 1 2/9/09 The sky varies as Earth orbits the Sun • As the Earth orbits the Sun, the Sun appears to move along the Zodiac ecliptic. • At midnight, the stars on our meridian are opposite the Sun in The 13 Zodiacal constellations that our Sun the sky. covers-up (blocks) in the course of one year (used to be only 12) • Aquarius • Leo • Pisces • Libra • Aries • Virgo • Scorpius • Taurus • Ophiuchus • Gemini • Sagittarius • Cancer • Capricornus The Zodiacal Constellations that our Sun blocks in the course of one year (only 12 are shown here) North Star Aquarius Pisces Capricornus Aries 1 day Sagittarius Taurus Scorpius 365 days Libra Gemini Virgo Cancer Leo North Star Aquarius Pisces Capricornus In-class Activities: Seasonal Stars Aries 1 day Sagittarius • Work with a partner! Taurus Scorpius • Read the instructions and questions carefully.
    [Show full text]
  • The Hubble Space Telescope Proper Motion Collaboration HSTPROMO
    HSTPROMO The HST Proper Motion Collaboration Dark Matter in the Local Group Roeland van der Marel (STScI) Stellar Dynamics • Many reasons to understand the dynamics of stars, clusters, and galaxies in the nearby Universe • Formation: The dynamics contains an imprint of initial conditions • Evolution: The dynamics reflects subsequent (secular) evolution • Structure: dynamics and structure are connected • Mass: Tied to the dynamics through gravity è critical for studies of dark matter 2 Line-of-Sight (LOS) Velocities • Almost all observational knowledge of stellar dynamics derives from LOS velocities • Requires spectroscopy – Time consuming – Limited numbers of objects – Brightness limits • Yields only 1 component of motion – Limited insight from 1D information 2 – 3D velocities needed for mass modeling: M = σ 3D Rgrav / G • Many assumptions/unknowns in LOS velocity modeling 3 Proper Motions (PMs) • PMs provide much added information, either by themselves (2D) or combined with LOS data (3D) • Characteristic velocity accuracy necessary – 1 km/s at 7 kpc (globular cluster dynamics) – 10 km/s at 70 kpc (Milky Way halo/satellite dynamics) – 100 km/s at 700 kpc (Local Group dynamics) – 0.03c at 70 Mpc (AGN jet dynamics) • Corresponding PM accuracy – 30 μas / yr (~ speed of human hair growth at Moon distance) • Observations – Ground-based: NO – VLBI: LIMITED (some water masers) – GAIA: FUTURE (but not crowded or faint) – HST: YES (0.006 HST ACS/WFC pixels in 10 yr) 4 Proper Motions with Hubble • Key Characteristics: – High spatial resolution – Low sky background – Exquisite telescope stability – Long time baselines – Large Archive – Many background galaxies in any moderately deep image • Advantages: – Depth: Astrometry of faint sources – Multiplexing: Many sources per field (N = 102 –106, Δ~ 1/√N) 5 HSTPROMO: The Hubble Space Telescope Proper Motion Collaboration (http://www.stsci.edu/~marel/hstpromo.html) • Set of many HST investigations aimed at improving our dynamical understanding of stars, clusters, and galaxies in the nearby Universe through PMs.
    [Show full text]
  • Polarization Fields and Phase Space Densities in Storage Rings: Stroboscopic Averaging and the Ergodic Theorem
    Physica D 234 (2007) 131–149 www.elsevier.com/locate/physd Polarization fields and phase space densities in storage rings: Stroboscopic averaging and the ergodic theorem✩ James A. Ellison∗, Klaus Heinemann Department of Mathematics and Statistics, University of New Mexico, Albuquerque, NM 87131, United States Received 1 May 2007; received in revised form 6 July 2007; accepted 9 July 2007 Available online 14 July 2007 Communicated by C.K.R.T. Jones Abstract A class of orbital motions with volume preserving flows and with vector fields periodic in the “time” parameter θ is defined. Spin motion coupled to the orbital dynamics is then defined, resulting in a class of spin–orbit motions which are important for storage rings. Phase space densities and polarization fields are introduced. It is important, in the context of storage rings, to understand the behavior of periodic polarization fields and phase space densities. Due to the 2π time periodicity of the spin–orbit equations of motion the polarization field, taken at a sequence of increasing time values θ,θ 2π,θ 4π,... , gives a sequence of polarization fields, called the stroboscopic sequence. We show, by using the + + Birkhoff ergodic theorem, that under very general conditions the Cesaro` averages of that sequence converge almost everywhere on phase space to a polarization field which is 2π-periodic in time. This fulfills the main aim of this paper in that it demonstrates that the tracking algorithm for stroboscopic averaging, encoded in the program SPRINT and used in the study of spin motion in storage rings, is mathematically well-founded.
    [Show full text]
  • Approximations in Numerical Analysis, Cont'd
    Jim Lambers MAT 460/560 Fall Semester 2009-10 Lecture 7 Notes These notes correspond to Section 1.3 in the text. Approximations in Numerical Analysis, cont'd Convergence Many algorithms in numerical analysis are iterative methods that produce a sequence fαng of ap- proximate solutions which, ideally, converges to a limit α that is the exact solution as n approaches 1. Because we can only perform a finite number of iterations, we cannot obtain the exact solution, and we have introduced computational error. If our iterative method is properly designed, then this computational error will approach zero as n approaches 1. However, it is important that we obtain a sufficiently accurate approximate solution using as few computations as possible. Therefore, it is not practical to simply perform enough iterations so that the computational error is determined to be sufficiently small, because it is possible that another method may yield comparable accuracy with less computational effort. The total computational effort of an iterative method depends on both the effort per iteration and the number of iterations performed. Therefore, in order to determine the amount of compu- tation that is needed to attain a given accuracy, we must be able to measure the error in αn as a function of n. The more rapidly this function approaches zero as n approaches 1, the more rapidly the sequence of approximations fαng converges to the exact solution α, and as a result, fewer iterations are needed to achieve a desired accuracy. We now introduce some terminology that will aid in the discussion of the convergence behavior of iterative methods.
    [Show full text]
  • The Beginners Guide to Astrology AQUARIUS JAN
    WHAT’S YOUR SIGN? the beginners guide to astrology AQUARIUS JAN. 20th - FEB. 18th THE WATER BEARER ften simple and unassuming, the Aquarian goes about accomplishing goals in a quiet, often unorthodox ways. Although their methods may be unorth- Oodox, the results for achievement are surprisingly effective. Aquarian’s will take up any cause, and are humanitarians of the zodiac. They are honest, loyal and highly intelligent. They are also easy going and make natural friendships. If not kept in check, the Aquarian can be prone to sloth and laziness. However, they know this about themselves, and try their best to motivate themselves to action. They are also prone to philosophical thoughts, and are often quite artistic and poetic. KNOWN AS: The Truth Seeker RULING PLANET(S): Uranus, Saturn QUALITY: Fixed ELEMENT: Air MOST COMPATIBILE: Gemini, Libra CONSTELLATION: Aquarius STONE(S): Garnet, Silver PISCES FEB. 19th - MAR. 20th THE FISH lso unassuming, the Pisces zodiac signs and meanings deal with acquiring vast amounts of knowledge, but you would never know it. They keep an Aextremely low profile compared to others in the zodiac. They are honest, unselfish, trustworthy and often have quiet dispositions. They can be over- cautious and sometimes gullible. These qualities can cause the Pisces to be taken advantage of, which is unfortunate as this sign is beautifully gentle, and generous. In the end, however, the Pisces is often the victor of ill cir- cumstance because of his/her intense determination. They become passionately devoted to a cause - particularly if they are championing for friends or family. KNOWN AS: The Poet RULING PLANET(S): Neptune and Jupiter QUALITY: Mutable ELEMENT: Water MOST COMPATIBILE: Gemini, Virgo, Saggitarius CONSTELLATION: Pisces STONE(S): Amethyst, Sugelite, Fluorite 2 ARIES MAR.
    [Show full text]
  • Finding the Planets Use the Charts Below to Find the Approximate Location of a Planet
    Finding the Planets Use the charts below to find the approximate location of a planet. If the month is blank the planet is not easily visible. Compare the constellation’s stars you see in the sky to the star charts on pages 10 and 11. The bright “star” that is not printed on the star chart will be the planet. Look for Mercury and Venus near the horizon in the morning about an hour before Sunrise (East) or in the evening about an hour after Sunset (West). Look for Mercury a few days before or after the date listed. Here is a tip: planets do not “twinkle”; stars do. An easy to use monthly star chart showing constellations, planets and other objects may be downloaded from www.skymaps.com To make your own accurate sky charts and find the exact location of a planet on any day from any location in the world, you can download the following free planetarium software. Cartes du Ciel: http://www.stargazing.net/astropc Hallo Northern Sky: http://www.hnsky.org/software.htm 2009 JAN FEB MAR APR MAY JUN MERCURY 4th Eve. 13th Morn. 26th Eve. 13th Morn. VENUS Evening Evening Morning Morning MARS Aries JUPITER Capricornus Capricornus Capricornus SATURN Leo Leo Leo Leo Leo Leo JUL AUG SEP OCT NOV DEC MERCURY 24th Eve. 6th Eve. 18th Eve. VENUS Morning Morning Morning MARS Taurus Taurus Gemini Cancer Cancer Leo JUPITER Capricornus Capricornus Capricornus Capricornus Capricornus Capricornus SATURN Leo Virgo Virgo 2010 JAN FEB MAR APR MAY JUN MERCURY 27th Morn. 8th Eve. 26th Morn.
    [Show full text]