DOCSLIB.ORG

Mathematical Modelling, Analysis and Simulations to Improve the Control of Miridae, a Cocoa Pest

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mathematical Modelling, Analysis and Simulations to Improve the Control of Miridae, a Cocoa Pest REPUBLIQUE DU CAMEROUN REPUBLIC OF CAMEROON Paix - Travail - Patrie Peace - Work - Fatherland ----------------- ----------------- UNIVERSITE DE DOUALA THE UNIVERSITY OF DOUALA ----------------- ----------------- ECOLE DOCTORALE DES SCIENCES POSTGRADUATE SCHOOL FOR FONDAMENTALES ET APPLIQUEES PURE AND APPLIED SCIENCE ----------------- ----------------- Unité de Formation Doctorale Postgraduate Training Unit for de Mathématiques, Informatique Mathematics, Applied Computer Appliquée et Physique Fondamentale Science and Pure Physics ----------------- ----------------- Laboratoire de Mathématiques Laboratory of Mathematics BP 24157 Douala PO Box 24157 Douala Email: [email protected] Email: [email protected] MATHEMATICAL MODELLING, ANALYSIS AND SIMULATIONS TO IMPROVE THE CONTROL OF MIRIDAE, A COCOA PEST THESIS defended publicly on June 19, 2020 in fulfillment of the requirements for the award of DOCTORAT / Ph.D in Applied Mathematics Specialty MATHEMATICAL MODELLING By DJOUKWE TAPI Myriam Sonia DEA in Applied Mathematics Registration number: 08S02819 Jury: President: OWONO ONANA Charles Professor The University of Douala Reporters: SALLET Gauthier Professor Université de Lorraine NGWA Gidéon Associate Professor University of Buea FONO Louis Aimé Associate Professor The University of Douala Advisors: BOWONG Samuel Professor The University of Douala DUMONT Yves Director of Research CIRAD BAGNY BEILHE Leila Researcher CIRAD Academic Year: 2018-2019 MATHEMATICAL MODELLING, ANALYSIS AND SIMULATIONS TO IMPROVE THE CONTROL OF MIRIDAE, A COCOA PEST DJOUKWE TAPI Myriam Sonia Academic Year: 2018/2019 Dedication To My late father TAPI Jean Pierre, Dad, you left early and you did not have the grace to see your daughter shine. Father, I miss you so much and you will always be in my heart. My mother MANGWA Rosalie, Mom, Thanks for all your love, all your sacrifices and efforts made during all these years for me. Doctorate Thesis i Remerciements La préparation de cette thèse a nécessité l’intervention de plusieurs personnes sans lesquelles ce travail n’aurait pas abouti. C’est pourquoi, je tiens à remercier tous ceux qui ont contribué à la préparation de ce travail. Je remercie Dieu le père tout puissant pour le don de la vie et pour son infinie assistance. L’immense rôle joué par mes encadrants Pr Samuel Bowong (Chef de Département de Math- ématiques et Informatique, Université de Douala, Cameroun), Pr Yves Dumont (Professeur ex- traordinaire, Université de Pretoria, CIRAD/AMAP) and Dr Leila Bagny-Beilhe (Chargé de la recherche, CIRAD), ne sera en aucun cas quantifié pour façonner mon potentiel de recherche et réaliser mon rêve de devenir Docteur en Mathématiques et œuvrer au développement de la com- munauté scientifique. Je vous remercie très sincèrement pour votre patience, vos conseils et votre enthousiasme tout au long de ma période d’étude. L’énorme soutien (financier) et vos contributions (nouvelles idées mathématiques et différents séminaires) ont conduit à la concrétisation de ce projet de recherche. Monsieur le Professeur Samuel Bowong, vous avez accepté de me faire partager vos activités de recherche en me proposant de réaliser mon mémoire de Master 2, puis ma thèse de doc- torat sous votre direction. Vous m’avez toujours honoré de votre confiance durant tout ce temps en me conseillant et en me tenant par la main. Vous m’avez laissé prendre des initiatives, et vous avez constamment été présent pour orienter et corriger mon travail. Nos discussions ainsi que votre vision toute particulière pour aborder les questions scientifiques m’ont beaucoup influencé et ont grande- ment contribué à développer mon jeune esprit d’apprenti chercheur. Je ne vous remercierai jamais assez pour tout ce que vous m’avez appris. De plus, je remercie tout particulièrement le Professeur Yves Dumont. Par votre amour du travail bien fait et par votre rigueur, vous avez développé en moi un intérêt particulier pour la recherche en biologie mathématique. J’ai réellement apprécié travaillé avec vous, nos différents échanges par mails, vos différents séjours ici au Cameroun durant ma thèse et surtout le séjour que j’ai effectué au centre de recherche AMAP, Montpellier n’ont fait qu’apprécier le travail à vos côtés. Vous m’avez fourni durant ces différentes séances de travail de précieux conseils et surtout de la critique en vue de l’amélioration de mon travail. Docteur Leila Bagny-Beilhe, vous avez toujours ménagé de votre temps chaque fois que je rencontrais des difficultés. J’apprécie Doctorate Thesis ii tous les encouragements à mon égard et toutes les critiques apportées durant ces années de travail. N’étant pas mathématicienne de formation, j’ai sincèrement apprécié tous les efforts consentis pour comprendre toutes les grosses formules mathématiques: ce n’était pas toujours facile de passer d’un langage à l’autre; mais avec nos différentes séances de travail on a toujours réussi à se comprendre. Merci chers encadrants pour le chercheur que je suis devenu. Mes remerciements vont à l’endroit de tout le staff académique et administratif de l’Université de Douala pour les différentes opportunités et facilités pour la réalisation de ce travail. Un merci particulier à tous les rapporteurs de cette thèse. Vous avez sacrifié de votre temps pour apporter votre part de contribution à l’amélioration de ce travail à travers vos idées et vos recommandations. Merci à l’équipe projet EPITAG à travers le laboratoire LIRIMA; à l’équipe projet GRIMCAPAE et UMMISCO, au DP/PCP Agroforesterie Cameroun, au CIRAD, l’IRD et l’INRIA/LIRIMA pour le support logsistique et financier durant la préparation et la finalisation de cette thèse. Je remercie tous les membres de l’UMR AMAP et de l’équipe projet BIOCORE pour leur esprit d’équipe durant mon séjour à leurs côtés. J’ai vraiment appris de vous. Je remercie tous les enseignants du département de Mathématiques et Informatique de l’Université de Douala et tous les enseignants du département de Mathématiques de l’Université de Yaoundé I pour toute votre aide et vos enseignements. Que cette soutenance soit pour vous l’accomplissement d’un dur labeur. Plus particulièrement Pr Jean Jules Tewa, Pr Louis Aimé Fono, Dr Anatole Temgoua, Dr Ferdinand Ngakeu, Dr Armand Tsimi, Dr Bertrand Mbama, merci pour tous vos conseils et pour la patience que vous avez toujours eu à mon égard. Dr Roger Tagne Wafo, merci pour votre assistance et votre support inconditionnel. Durant toutes ces années, vous avez été et vous êtes un père pour moi; vous m’avez toujours encouragé à me surpasser et à aller de l’avant. Merci pour tous ces sacrifices consentis à ma juste personne. Je remercie mes camarades de promotion et mes ainés: Dr Plaire Tchinda, Dr Alexis Tchuinte, Dr Valaire Yatat, Dr Gabriel Kolaye, Dr Yannick Malong, Dr Vidal Kamdem, Dr Janvier Ntahomvukiye, Justin Dzuche, Luther Mann, Yves Fotso. Merci pour votre support et votre collaboration, vous m’avez toujours prêté une oreille attentive. Je remercie tous les membres du laboratoire de Mathématiques de l’Université de Douala spéciale- ment tous les membres de l’équipe "Team Mathematical Modelling" pour tous vos encouragements et pour votre esprit d’équipe. J’ai vraiment aimé travaillé avec vous. Je pense spécialement à Camelle Kabiwa, Yssel Hyonta, Cédric Hameni et Clotilde Djuikem. Merci à mes amis, mon autre famille. Je pense particulièrement à Giresse Noubissie, Hermann Doctorate Thesis iii Tafo, Boris Njike, Eddy Kowa, Sophie Menkui, Armel Foko, Floriane Fondop, Giresse Essouan, Franc Djapa, Ismael Ngounou, Carole Djokam et Félicité Barth Nkamen. Merci pour votre disponibilité et votre attention à mon égard durant toutes ces années. Merci à vous tous qui avez toujours été là pour moi et qui m’avez toujours soutenu. Je pense particulièrement aux prêtres: les abbés René Ngon, Michel Tchoumbou, Henri-Joel Ndjeyep, Meinrad Hebga, Dimitri Chokouago, le couple Mbolda et mes amis Ulrich Nguemdjo, Yannick Foadjo, Sandra Mbialeu, Corneille Megaptche, Nathalie Matsinkou, Alphonsine Massu, Cabrelle Ndjodo. Merci pour toutes vos prières. Il n’y a pas un jour qui passe sans que je ne pense avec amour à mes parents précisement à ma maman Mangwa Rosalie. Les valeurs que tu m’as enseigné ne cessent de guider mes pas. Que cette thèse soit le témoignage que tout ceci n’ait pas été vain. Sachez que je t’aime de tout mon coeur. Merci à ma grand mère Nguenang Elise, à vous mes frères et soeurs: Dimitri, Flavien, William, Michelle et Claude; mes oncles Joseph Ledoux Teponou, Calvin Njayong, Etienne Yankou et mon cousin Mohoue Jacques pour votre amour, votre patience, votre support et tous les sacrifices consentis dans la réalisation de projet. Enfin, nous disons merci à tous ceux qui de près ou de loin ont contribué à la réalisation de ce travail. Recevez l’expression de ma profonde gratitude et de ma sympathie. Doctorate Thesis iv Contents Dedication i Remerciements ii Abstract xii Résumé xiii General Introduction1 1 Literature review and Mathematical tools4 1.1 The cacao tree: Theobroma cacao ..............................4 1.1.1 Origin and importance................................4 1.1.2 Characteristics of agroforests in Cameroon....................6 1.1.3 Phenology and physioloygy of cacao tree Theobroma cacao ............9 1.1.4 Diseases and bugs of T. cacao ............................ 12 1.2 Cacao mirids......................................... 12 1.2.1 The cacao mirid: Sahlbergella singularis ...................... 13 1.2.1.1 Presentation of Sahlbergella singularis .................. 13 1.2.2 Life cycle of S.singularis
Load more

Recommended publications
  • List of Reviewers 2018
    List of Reviewers (as per the published articles) Year: 2018 International Journal of TROPICAL DISEASE & Health ISSN: 2278-1005 2018 - Volume 29 [Issue 1] DOI: 10.9734/IJTDH/2018/38804 (1) Victoria Katawera-Nyanzi, Liberia. (2) Ruqayyah Hamidu Muhammad, Federal University, Nigeria. Complete Peer review History: http://www.sciencedomain.org/review-history/22893 DOI: 10.9734/IJTDH/2018/39170 (1) Sanjay Kumar Gupta, Saudi Arabia. (2) Omotowo Babatunde, University of Nigeria, Nigeria. Complete Peer review History: http://www.sciencedomain.org/review-history/22977 DOI: 10.9734/IJTDH/2018/39180 (1) Ketan Vagholkar, D. Y. Patil University, School of Medicine, India. (2) Claudia Irene Menghi, University of Buenos Aires, Argentina. Complete Peer review History: http://www.sciencedomain.org/review-history/23098 DOI: 10.9734/IJTDH/2018/36283 (1) Shari Lipner, Weill Cornell Medicine, USA. (2) K. R. Raghavendra, Mysore Medical College and Research Institute, India. Complete Peer review History: http://www.sciencedomain.org/review-history/23157 DOI: 10.9734/IJTDH/2018/39099 (1) Ali Kemal Erenler, Hitit University, School of Medicine, Turkey. (2) Justin Agorye Ingwu, University of Nigeria, Nigeria. (3) Franco Mantovan, University of Verona, Italy. Complete Peer review History: http://www.sciencedomain.org/review-history/23158 2018 - Volume 29 [Issue 2] DOI: 10.9734/IJTDH/2018/39726 (1) Emmanuel O. Adesuyi, Institute of Nursing Research, Nigeria. (2) Joyce Kinaro, University of Nairobi, Kenya. Complete Peer review History: http://www.sciencedomain.org/review-history/23248 DOI: 10.9734/IJTDH/2018/38538 (1) Bamidele Tajudeen, Nigerian Institute of Medical Research, Nigeria. (2) Tsaku Paul Alumbugu, Nasarawa State University, Nigeria. (3) Irfan Erol, Ankara University, Turkey.
    [Show full text]
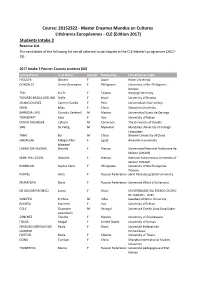
  • CLE (Edition 2017) Students Intake 2 Reserve List the Candidates of the Following List Are All Selected to Participate in the CLE Master's Programme (2017- 19)
    Course: 20152322 - Master Erasmus Mundus en Cultures Littéraires Européennes - CLE (Edition 2017) Students Intake 2 Reserve List The candidates of the following list are all selected to participate in the CLE Master's programme (2017- 19) 2017 Intake 2 Partner Country students (66) Family Name First Name Gender Nationality University of origin HIGUCHI Shoichi F Japan Hosei Univeristy GONZALES Gema Charmaine F Philippines University of the Philippines Diliman TSAI Li-Chi F Taiwan Nanjing University TAVARES BRAGA AVELINO Stella F Brazil University of Brasilia CHANG CHÁVEZ Carmen Cecilia F Peru Universidad César Vallejo CHEN Miao F China Shenzhen University BARBOSA LINO Gonzalo Centeotl M Mexico Universidad Vasco de Quiroga TORKBAYAT Sara F Iran University ofTehran EPOKO NOUBISSIE Calvain M Cameroon The University of Douala SWE Su Paing M Myanmar Mandalay University of Foreign Languages TANG Bo M China Renmin University of China GADALLAH Pelagia Adel F Egypt Alexandria university Moawad LABASTIDA SALINAS Daniela F Mexico Universidad Nacional Autónoma de México (UNAM) MARTINEZ COLIN Gabriela F Mexico National Autonomous University of Mexico (UNAM) ROMBLON Sophia Clariz F Philippines University of the Philippines Diliman KURPEL Alina F Russian Federation Saint Petersburg State University MURATOVA Daria F Russian Federation Université d'Etat d'Oulianovsk DE AGUIAR PACHECO Laura F Brazil UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO - UERJ SANJEEVI Krithika M India Jawaharlal Nehru University ROOSTA Fatemeh F Iran University ofTehran COLY Ousmane
    [Show full text]
  • A Systematic Review of the Spectrum of Cardiac Arrhythmias in Sub-Saharan Africa
    Yuyun MF, et al. A Systematic Review of the Spectrum of Cardiac Arrhythmias in Sub-Saharan Africa. Global Heart. 2020; 15(1): 37. DOI: https://doi.org/10.5334/gh.808 ORIGINAL RESEARCH A Systematic Review of the Spectrum of Cardiac Arrhythmias in Sub-Saharan Africa Matthew F. Yuyun1,2, Aimé Bonny3,4,5, G. André Ng6, Karen Sliwa7, Andre Pascal Kengne8, Ashley Chin9, Ana Olga Mocumbi10, Marcus Ngantcha4, Olujimi A. Ajijola11 and Gene Bukhman1,12,13,14 1 Department of Medicine, Harvard Medical School, Boston, US 2 Cardiology and Vascular Medicine Service, VA Boston Healthcare System, Boston, US 3 District Hospital Bonassama, Douala/University of Douala, CM 4 Homeland Heart Centre, Douala, CM 5 Centre Hospitalier Montfermeil, Unité de Rythmologie, Montfermeil, FR 6 National Institute for Health Research Leicester Biomedical Research Centre, Department of Cardiovascular Sciences, University of Leicester, UK 7 Hatter Institute for Cardiovascular Research in Africa, University of Cape Town, ZA 8 South African Medical Research Council and Department of Medicine, University of Cape Town, ZA 9 The Cardiac Clinic, Department of Medicine, Groote Schuur Hospital and University of Cape Town, ZA 10 Instituto Nacional de Saúde and Universidade Eduardo Mondlane, Maputo, MZ 11 Ronald Reagan UCLA Medical Center Los Angeles, US 12 Division of Cardiovascular Medicine and Division of Global Health Equity, Brigham and Women’s Hospital, Boston, US 13 Program in Global NCDs and Social Change, Department of Global Health and Social Medicine, Harvard Medical School, Boston, US 14 NCD Synergies project, Partners In Health, Boston, US Corresponding author: Matthew F. Yuyun, MD, MPhil, PhD ([email protected]) Major structural cardiovascular diseases are associated with cardiac arrhythmias, but their full spectrum remains unknown in sub-Saharan Africa (SSA), which we addressed in this systematic review.
    [Show full text]
  • Rachel Ayuk Ojong Diba Tel: (237) 77 18 24 26 Email
    CURRICULUM VITAE Name: Rachel Ayuk Ojong Diba Tel: (237) 77 18 24 26 Email: [email protected] Institution: University of Buea Po Box 63, Buea ………………………………………………………………………………………………… OBJECTIVE To merge my enthusiasm with my desire to grow and gain contemporary research experience in sociolinguistics and in teaching a wide variety of learners as well as contribute to the realization of the goals of your institution. ………………………………………………………………………………………………… EDUCATIONAL BACKGROUND v October 2013- present: University of Buea. PhD in Applied Linguistics expected in December 2017. Supervisors: Prof. Ayu’nwi Neba and Dr. Pierpaolo Di Carlo. Thesis: The Sociolinguistic Dynamics of Rural Multilingualism-the case of Lower Fungom. An exploration of rural multilingualism in relation with notions such as polyglossia in a rural linguistically diverse community in Cameroon. v October 2008 – December 2011: The University of Buea. Master of Arts in Applied Linguistics, University of Buea. Supervisors: Prof. Chia and (then) Dr. Ayu’nwi Neba. Dissertation: Language Choice and Identity Negotiation_ Molyko. Examining the linguistic repertoire and the dynamics involved in language choice and use of individuals in a micro urban linguistically diverse area in Cameroon v October 2004 – December 2007: The University of Buea. Bachelor of Arts in General Linguistics University of Buea …………………………………………………………………………………………………. PROFESSIONAL EXPERIENCE v 2012- Present: Instructor: “The Use of English’ program”. Teaching and assessing the use of English course, a general University requirement, to students of various levels at the University of Buea, Cameroon. v 2014- Present: Instructor: The department of Linguistics at the University of Buea. Teaching sociolinguistics courses to 200 and 300 level students. v July and August of every year since 2012: Intensive English Language Programme.
    [Show full text]
  • Higher Education in Africa Phase III: Angela Gaffney, Alice Golenko, Identifying Successful Regional Networks & Hubs C
    Higher Education in Africa Phase III: Angela Gaffney, Alice Golenko, Identifying Successful Regional Networks & Hubs C. Leigh Anderson, & Mary Kay Gugerty EPAR Brief No. 230 Prepared for the Agricultural Policy Team of the Bill & Melinda Gates Foundation Professor Leigh Anderson, Principal Investigator Associate Professor Mary Kay Gugerty, Principal Investigator April 29, 2013 Overview This paper is the third in EPAR’s series on Higher Education in Africa. Our research tasks in this phase build on Phase I, in which we sought to identify measurable rates of return on tertiary agricultural education in Africa and describe the current state of African higher agricultural education (HAE), and Phase II, in which we identified countries’ experiences with national higher education capacity building through partnership building, cross-border opportunities such as ‘twinning,’ and various retention and diaspora engagement strategies. In this phase we discuss successful regional education models, particularly in Sub-Saharan Africa. We have organized our findings and analysis into three sections.The first section organizes the literature under categories of regional higher education models or ‘hubs’ and discusses measurement of the regional impact of higher education.The second section provides bibliometric data identifying academically productive countries and universities in Sub-Saharan Africa.The final section provides a list of regional higher education models identified in the literature and through a web-based review of existing higher education networks and hubs. We also include a list of challenges and responses to regional coordination. Approach We have identified several regional higher education models through a web-based literature review. We searched for peer- reviewed journal articles using Google Scholar and the University of Washington Library system using phrases such as “top universities Africa,” “higher education impact,” “transnational higher education Africa,” “regional hubs higher education,” “quality assurance education,” “regional education network”.
    [Show full text]
  • Surgical Outcome of Genito-Urinary Obstetric Fistulas
    Obstetrics & Gynecology International Journal Research Article Open Access Surgical outcome of genito-urinary obstetric fistulas (GUOF) with or without bladder neck involvement: an experience from the University Teaching Hospital, Yaoundé, Cameroon Summary Volume 10 Issue 3 - 2019 Surgical Outcome of Genito-urinary obstetric fistulas (GUOF) with or without bladder Pierre Marie Tebeu,1–4 Michel Ekono,5 Claude neck involvement: an experience from the University Teaching Hospital, Yaounde, 2 Cameroon Cyrille Noa Ndoua, Georges Didier Ngassa Meutchi,3 Yvette Nkene Mawamba,4 Charles- Introduction: The GUOF is a solution of continuity between the genital tract and the Henry Rochat6 urinary tract in connection with pregnancy or childbirth. The urethral involvement 1Inter-States High School for Public Health Training of Central seems to be associated to a bad prognosis. However, little is known about this issue. Africa (CIESPAC), Congo 2 Objective: To analyze the result of post-surgical GUOF with or without urethral Faculty of Medicine and Biomedical Sciences, University of Yaoundé I, Cameroon involvement. 3League for Initiative and Active Research for Women’s Health Methodology: It was a retrospective cohort study. We identified the files of the and Education (LIRASEF), Cameroon 4 patients with or without urethral involvement operated at the department of Obstetrics Department of Gynecology Obstetrics, University Teaching & Gynecology of UTH, Yaounde from March 03, 2009 to March 03, 2015 (six years). Hospital, Yaoundé-Cameroon 5 Data was collected from the files, registers, and by phone call from the participants Gynecologist and Lecturer, Faculty of Medicine and Pharmaceutical Sciences, University of Douala, Cameroon after oral consent. Variables included the sociodemographic, clinical and therapeutic 6Geneva Foundation for Medical Education and Research, patterns.
    [Show full text]
  • Foreword and Acknowledgements
    Foreword and Acknowledgements This Volume 20 of the African Development Perspectives Yearbook with the title “Science, Technology and Innovation Policies for Inclusive Growth in Africa. General Issues and Country Cases” has again benefited from many contributions, from various inputs and from important institutional support. The great number of contributions to this volume (essays, review articles and book reviews) was made possible because of the continuing support from African and international organisations, from numerous research and devel- opment institutions, and from many individual experts cooperating continu- ously with us on Africa. A great number of international and regional organi- sations, universities and research institutes have supported this project, such as: UNESCO (United Nations Educational, Scientific and Cultural Organisa- tion); the ACBF (African Capacity Building Foundation); UNECA (United Nations Economic Commission for Africa); the FAO (Food and Agriculture Organization) in Rome, Italy; UNCTAD (United Nations Conference on Trade and Development), Trade and Poverty Branch, Division for Africa, LDCs and Special Programmes in Geneva, Switzerland; the Department of Economics, University of Khartoum, Sudan; the Department of Agricultural Economics, Faculty of Agriculture, Usmanu Danfodiyo University, Sokoto, Nigeria; the Department of Agricultural Economics and Rural Sociology, Institute for Agricultural Research, Ahmadu Bello University, Zaria, Nigeria; the National Institute for Animal Production, Shika, Ahmadu
    [Show full text]
  • International Symposium Building the Tomorrow's Port City in Atlantic Africa Location: Kribi (Cameroon) Dates: 6-8 November 2017
    INTERNATIONAL SYMPOSIUM BUILDING THE TOMORROW'S PORT CITY IN ATLANTIC AFRICA LOCATION: KRIBI (CAMEROON) DATES: 6-8 NOVEMBER 2017 1. Context and rationale The "Atlantic Africa" project aims at understanding Africa in a different way than by the usual reading grids, based on outdated findings or tainted by pejorative presuppositions now denounced. It is a matter of demonstrating that Africa is a continent in motion, a continent of human mobility and flows of goods, capital, information, a continent of circulation, much more at ease in the processes of globalization than suggest certain statistics and dominant cultural representations. It is clear that Africa no longer turns its back on the sea. On a more theoretical level, it is also a question of drawing lessons from African experiences, in order to better understand the mechanisms of globalization, as much in its technical and economic aspects as well as in its environmental, geopolitical and cultural dimensions. Preceding this symposium, a symposium has already been held in Dakar in October 2015, and two symposiums in Cotonou, Marport 1 in 2015 and Marport 2 in 2016. A book in city within the Port, led by colleagues from Abidjan, is on the publication. 2. Issue and general objective The entry chosen to achieve this objective is the port city, both a link in globalized logistical chains, an interface between the exterior and the interior of Africa, dynamic foci of territorial configurations transformed by productive processes and urban deployment. Even though these port cities are also linked to the world by air transport and the digital revolution, the sea remains, however, the result of increased penetration of manufactured goods from elsewhere and an exit from the natural resources coveted by all.
    [Show full text]
  • Research4life Academic Institutions
    Research4Life Academic Institutions Filter Summary Country City Institution Name Afghanistan Bamyan Bamyan University Charikar Parwan University Cheghcharan Ghor Institute of Higher Education Ferozkoh Ghor university Gardez Paktia University Ghazni Ghazni University HERAT HERAT UNIVERSITY Herat Institute of Health Sciences Ghalib University Jalalabad Nangarhar University Alfalah University Kabul Afghan Medical College Kabul 18-Oct-2019 2:04 PM Prepared by Sharpe, Jenna Page 1 of 200 Country City Institution Name Afghanistan Kabul JUNIPER MEDICAL AND DENTAL COLLEGE Government Medical College Kabul University. Faculty of Veterinary Science Aga Khan University Programs in Afghanistan (AKU-PA) Kabul Dental College, Kabul Kabul University. Central Library American University of Afghanistan Agricultural University of Afghanistan Kabul Polytechnic University Kabul Education University Kabul Medical University, Public Health Faculty Cheragh Medical Institute Kateb University Prof. Ghazanfar Institute of Health Sciences Khatam al Nabieen University Kabul University of Medical Sciences Kandahar Kandahar University Malalay Institute of Higher Education Kapisa Alberoni University khost,city Shaikh Zayed University, Khost 18-Oct-2019 2:04 PM Prepared by Sharpe, Jenna Page 2 of 200 Country City Institution Name Afghanistan Lashkar Gah Helmand University Logar province Logar University Maidan Shar Community Midwifery School Makassar Hasanuddin University Mazar-e-Sharif Aria Institute of Higher Education, Faculty of Medicine Balkh Medical Faculty Pol-e-Khumri Baghlan University Samangan Samanagan University Sheberghan Jawzjan university Albania Elbasan University "Aleksander Xhuvani" (Elbasan), Faculty of Technical Medical Sciences Korca Fan S. Noli University, School of Nursing Tirana University of Tirana Agricultural University of Tirana 18-Oct-2019 2:04 PM Prepared by Sharpe, Jenna Page 3 of 200 Country City Institution Name Albania Tirana University of Tirana.
    [Show full text]
  • Choiseul-100-Africa-2015-VA.Pdf
    RANKING 2O15 AFRICA Economic Leaders for Tomorrow PARTNERS 2 Dr. Pascal Lorot President, Institut Choiseul fter remaining to the rim of the global This tremendous dynamic is linked to Aeconomy and the main financial and the emergence of a young economic commercial flows for a long time, Africa leading class, well trained, with an open is now considered as a central economic outlook, connected to global economic actor at a global scale. These last few years, and information flows generated by it even became an essential driving force of globalization. Those young leaders are global growth. shaping a modern African economy, open High performing activity can be to the world, with new opportunities spotted everywhere. Economic growth flourishing everywhere these days. is gaining all parts of the continent. Those young leaders are carrying the Africa is progressively stepping out of its future of their continent. They send a dependency to raw materials and is rapidly great message of hope. Africa has taken a becoming more diverse, by investing in successful start indeed ; it is willing to be higher added-value sectors. A middle class part of global growth and activity ! is rising in the meantime and is in demand This is the very reality the Choiseul 100 for better consumer goods, products that Africa intends to promote. As a unique used to be only for a restrictive elite until ranking of young African economic then. Centrality of Africa can also be leaders under forty years old and below, attributed to its tremendous demographic the study intends to highlights these dynamic — as one out of four individuals women and men who build today’s Africa will be African by 2050 — and it is why and prepare the one of tomorrow.
    [Show full text]
  • Spectrum of Meningitis in Adult at the Douala General Hospital
    World Journal of Neuroscience, 2014, 4, 144-151 Published Online May 2014 in SciRes. http://www.scirp.org/journal/wjns http://dx.doi.org/10.4236/wjns.2014.42017 Spectrum of Meningitis in Adult at the Douala General Hospital Yacouba N. Mapoure1,2, Henry N. Luma2,3, Dieudonné Gnonlonfoun4, Paul M. Ossou-Guiet5, Xaverie Biloa1, Jacques N. Doumbe1,2, Hugo Bertrand N. Mbatchou1,2, Benjamin Clet N. Tchaleu6, Julius Y. Fonsah7, Albert S. Mouelle1,2, Alfred K. Njamnshi7,8 1Department of Clinical Sciences, The University of Douala, Douala, Cameroon 2Department of Clinical Sciences, Douala General Hospital, Douala, Cameroon 3Department of Internal Medicine, The University of Yaoundé I, Yaoundé, Cameroon 4Department of Neurology, National University Hospital Centre, Cotonou, Bénin 5Department of Neurology, Brazzaville University Teaching Hospital, Brazzaville, Congo 6Department of Clinical Sciences, Université des Montagnes, Douala, Cameroon 7Department of Neurology, Yaoundé Central Hospital, Yaoundé, Cameroon 8Department of Neurology, The University of Yaoundé I, Yaoundé, Cameroon Email: [email protected] Received 1 January 2014; revised 1 February 2014; accepted 8 February 2014 Copyright © 2014 by authors and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract Objectives: Describe the clinical, aetiological and prognostic features of infectious meningitis in adults at the Douala General Hospital (DGH). Patients and Methods: We carried out a 5-year ret- rospective cross-sectional study at the DGH, on data from the registers of the bacteriology and biochemistry laboratories. Cases of meningitis were identified from the results of the cerebrospi- nal fluid (CSF) analysis, and the patient clinical file was obtained.
    [Show full text]
  • Differentiation and Articulation in Tertiary Education Systems Is Part of the World Bank Working Paper Series
    44178 WORLD BANK WORKING PAPER NO. 145 NO. 145 NO. AFRICA HUMAN DEVELOPMENT SERIES Differentiation and Articulation in Tertiary Education Systems is part of the World Bank Working Paper series. Differentiation and Articulation in These papers are published to communicate the results of Public Disclosure Authorized the Bank’s ongoing research and to stimulate public discus- sion. Tertiary Education Systems This paper explores an area of tertiary education that is currently understudied—the extent and nature of differentia- Differentiation and ArticulationDifferentiation Tertiary and in Systems Education tion and articulation in African tertiary education systems. A Study of Twelve Countries The overall finding of the study is that a binary system is dominant, characterized by universities and polytechnics as distinct types of institutions. Differentiation is clearly evident in Africa, though mostly horizontal as opposed to vertical. Articulation, on the other hand, seems to be in its infancy, as some universities, in their admission requirements, do not Njuguna Ng’ethe recognize polytechnic qualifications, and mobility between George Subotzky similar institution types is rare. National policy, market George Afeti Public Disclosure Authorized forces, institutional reforms, industry, and regional initiatives drive differentiation. Resource constraints, isomorphism, governance and funding structures, and the absence of debate over size and shape act as inhibitors. Demand for access appears to be the only driver for articulation, while national
    [Show full text]