DOCSLIB.ORG

Edexcel Advanced Extension Award Mathematics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Edexcel Advanced Extension Award Mathematics ^b^ péÉÅáãÉå=m~éÉê=~åÇ=j~êâ=pÅÜÉãÉ bÇÉñÅÉä=^Çî~åÅÉÇ=bñíÉåëáçå=^ï~êÇ j~íÜÉã~íáÅë=EVUMNF cçê=cáêëí=bñ~ãáå~íáçå pìããÉê=OMMO bÇÉñÅÉä=áë=çåÉ=çÑ=íÜÉ=äÉ~ÇáåÖ=Éñ~ãáåáåÖ=~åÇ=~ï~êÇáåÖ=ÄçÇáÉë=áå=íÜÉ=rh=~åÇ=íÜêçìÖÜçìí íÜÉ=ïçêäÇK==tÉ=éêçîáÇÉ=~=ïáÇÉ=ê~åÖÉ=çÑ=èì~äáÑáÅ~íáçåë=áåÅäìÇáåÖ=~Å~ÇÉãáÅI=îçÅ~íáçå~äI çÅÅìé~íáçå~ä=~åÇ=ëéÉÅáÑáÅ=éêçÖê~ããÉë=Ñçê=ÉãéäçóÉêëK qÜêçìÖÜ=~=åÉíïçêâ=çÑ=rh=~åÇ=çîÉêëÉ~ë=çÑÑáÅÉëI=bÇÉñÅÉäDë=ÅÉåíêÉë=êÉÅÉáîÉ=íÜÉ=ëìééçêí=íÜÉó åÉÉÇ=íç=ÜÉäé=íÜÉã=ÇÉäáîÉê=íÜÉáê=ÉÇìÅ~íáçå=~åÇ=íê~áåáåÖ=éêçÖê~ããÉë=íç=äÉ~êåÉêëK cçê=ÑìêíÜÉê=áåÑçêã~íáçå=éäÉ~ëÉ=Å~ää=çìê=`ìëíçãÉê=oÉëéçåëÉ=`ÉåíêÉ=çå=MUTM=OQM=VUMMI=çê îáëáí=çìê=ïÉÄëáíÉ=~í=ïïïKÉÇÉñÅÉäKçêÖKìâ g~åì~êó=OMMO mìÄäáÅ~íáçåë=`çÇÉ=r^ ^ää=íÜÉ=ã~íÉêá~ä=áå=íÜáë=éìÄäáÅ~íáçå=áë=ÅçéóêáÖÜí «=g~åì~êó=OMMO=bÇÉñÅÉä bÇÉñÅÉä=cçìåÇ~íáçå=áë=~=êÉÖáëíÉêÉÇ=ÅÜ~êáíó=~åÇ=~=Åçãé~åó=äáãáíÉÇ=Äó=Öì~ê~åíÉÉK oÉÖáëíÉêÉÇ=áå=båÖä~åÇ=kçK=NSUSNSQ CONTENTS Page 9801 AEA Mathematics Specimen Paper 5 Specimen Markscheme 10 Guidance for centres 16 Guidance for students 19 Paper Reference(s) 9801 Mathematics Advanced Extension Award Materials required for examination Items included with question papers Answer Book (AB16) Nil Graph Paper (ASG2) Mathematical Formulae (Lilac) Candidates may NOT use calculators in answering this paper. Instructions to Candidates Full marks may be obtained for answers to ALL questions. In the boxes on the answer book provided, write the name of the examining body (Edexcel), your centre number, candidate number, the paper title, the paper reference (9801), your surname, other names and signature. Information for Candidates A booklet ‘Mathematical Formulae including Statistical Formulae and Tables’ is provided. Full marks may be obtained for answers to ALL questions. This paper has seven questions. Advice to Candidates You must ensure that your answers to parts of questions are clearly labelled. You must show sufficient working to make your methods clear to the examiner. Answers without working may gain no credit. Printer’s Log No. -----/----- This publication may only be reproduced in accordance with QCA copyright policy. Turn over © 2001 QCA. 1. (a) By considering the series 1+ t + t 2 + t 3 +K+ t n , or otherwise, sum the series 1 + 2t + 3t 2 + 4t 3 + K + nt n −1 for t ≠ 1. (5) (b) Hence find and simplify an expression for 1+ 2× 3 + 3× 32 + 4 × 33 +K+ 2001× 32000 . (1) (c) Write down an expression for both the sums of the series in part (a) for the case where t = 1. (1) π π 2 ó 2x ó 2 2. Given that S = ô e sin x dx and C = ô e 2x cos x dx, õ0 õ0 (a) show that S = 1 + 2C, (3) (b) find the exact value of S. (6) 3. Solve for values of θ, in degrees, in the range 0 ≤ θ ≤ 360, √2 × (sin 2θ + cos θ ) + cos 3θ = sin 2θ + cosθ. (12) 6 4. A curve C has equation y = f(x) with f ′(x) > 0. The x-coordinate of the point P on the curve is a. The tangent and the normal to C are drawn at P. The tangent cuts the x-axis at the point A and the normal cuts the x-axis at the point B. (a) Show that the area of ∆APB is æ []′ 2 + ö 1 2 ç f (a) 1÷ []f (a) ç ÷ . 2 è f ′(a) ø (8) (b) Given that f(x) = e5x and the area of ∆APB is e5a , find and simplify the exact value of a. (4) 5. The function f is defined on the domain [–2, 2] by: ì− kx(2 + x) if − 2 ≤ x < 0, f (x) = í î kx(2 − x) if 0 ≤ x ≤ 2, where k is a positive constant. The function g is defined on the domain [–2, 2] by g(x) = (2.5) 2 − x 2 . (a) Prove that there is a value of k such that the graph of f touches the graph of g. (8) (b) For this value of k sketch the graphs of the functions f and g on the same axes, stating clearly where the graphs touch. (4) (c) Find the exact area of the region bounded by the two graphs. (5) 7 6. Given that the coefficients of x, x² and x 4 in the expansion of ()1+ kx n , where n ≥ 4 and k is a positive constant, are the consecutive terms of a geometric series, 6(n −1) (a) show that k = . (n − 2)(n − 3) (6) (b) Given further that both n and k are positive integers, find all possible pairs of values for n and k. You should show clearly how you know that you have found all possible pairs of values. (5) (c) For the case where k = 1.4, find the value of the positive integer n. (2) (d) Given that k = 1.4, n is a positive integer and that the first term of the geometric series is the coefficient of x, estimate how many terms are required for the sum of the × 12 ≈ geometric series to exceed 1.12 10 . [You may assume that log10 4 0.6 and ≈ log10 5 0.7. ] (5) 8 7. The variable y is defined by = 2 + 2 < < π y ln (sec x cosec x) for 0 x 2 . A student was asked to prove that dy = −4 cot 2x. dx The attempted proof was as follows: y = ln (sec 2 x + cosec 2 x) = ln (sec 2 x) + ln (cosec 2 x) = 2ln sec x + 2ln cosec x dy = 2 tan x − 2cot x dx 2 − 2 = 2(sin x cos x) sin x cos x − = 2cos 2x 1 2 sin 2x = −4cot 2x (a) Identify the error in this attempt at a proof. (1) (b) Give a correct version of the proof. (5) (c) Find and simplify a general relationship between p and q, where p and q are variables that depend on x, such that the student would obtain the correct result when differentiating ln (p + q) with respect to x by the above incorrect method. (8) (d) Given that p(x) = k sec rx and q(x) = cosec² x, where k and r are positive integers, find the values of k and r such that p and q satisfy the relationship found in part (c). (4) END Marks for presentation: 7 TOTAL MARKS: 100 9 ADVANCED EXTENSION AWARD in MATHEMATICS SPECIMEN PAPER – MARK SCHEME No Working Marks 1(a) n+1 − M1 = t 1 G.P. a = 1, r = t, S n A1 t −1 − d S =1+ 2t +K+ nt n 1 = (1st series) M1 dt d ()()t −1 n +1 t n − (t n+1 −1).1 Quotient M1 ()S = dt n ()t −1 2 rule A1 n+1 − ()+ n + = nt n 1 t 1 ()t −1 2 (5) (b) t = 3, n = 2001 2001.32002 − 2002.32001 +1 4001.32001 +1 B1 Þ Sum = = (1) 22 4 + − n()n +1 (c) 1+ t +K+ t n 1 → n + 1 ; 1+ 2t +K + nt n 1 → B1 (both) 2 (1) (7) 2(a)π π M1 2 π 2 = 2x ()− = []− 2x 2 + 2x A1 (ignore S ò e d cos x dx cos x e 0 2ò e cos x dx 0 0 limits) S = ()()− 0 − −1 + 2C or 1+ 2C A1 cso (3) π π (b) 2 π 2 M1 = 2x ()= []2x 2 − 2x C ò e d sin x sin xe 0 2ò e sin xdx A1 (ignore 0 0 limits) C = ()eπ − ()0 − 2S i.e. C = eπ − 2S A1 Solving S =1+ 2()eπ − 2S M1 =1+ 2eπ − 4S π 1 π M1, A1 5S =1+ 2e and S = ()1+ 2e 5 (6) (9) 10 ADVANCED EXTENSION AWARD in MATHEMATICS SPECIMEN PAPER – MARK SCHEME No Working Marks 3 ( 2 −1)()sin 2θ + cosθ + cos3θ = 0 M1 ()2 −1 cosθ ()1+ 2sinθ + cos3θ = 0 cos3θ ≡ cos 2θ cosθ − sin 2θ sinθ M1 ≡ cosθ []cos 2θ − 2sin 2 θ M1 ≡ cosθ []1− 4sin 2 θ A1 So: cosθ (( 2 −1)()()()1+ 2sinθ + 1− 2sinθ 1+ 2sinθ )= 0 M1 i.e. cosθ ()1+ 2sinθ ( 2 −1+1− 2sinθ )= 0 M1 i.e. 2 cosθ ()1+ 2sinθ (1− 2 sinθ )= 0 M1 cosθ = 0 Þ θ = 90°, 270° A1 (both) + θ = Þ θ = − 1 Þ θ = ° ° A1, A1 1 2sin 0 sin 2 210 , 330 A1, A1 1− 2 sinθ = 0 Þ sinθ = 1 Þ θ = 45°, 135° 2 (12) 4(a) y Equation of tangent: y – f(a) = f ′(a)(x – a) M1 P æ f ()a ö A1 Þ A is ça − ,0÷ f(x) è f ′()a ø O A B x 1 Gradient of normal is − ; f ′()a M1 1 Equation of normal : y − f ()a = − ()x − a M1 f ′()a Þ B is ()a + f ()()a f ′ a ,0 A1 é f ()a ù M1, A1 Area ∆APB is 1 AB.f ()a = 1 f ()a êf ()a f ′ ()a + ú 2 2 ë f ′()a û æ []f ′()a 2 +1ö = 1 []()2 ç ÷ A1 c.s.o. 2 f a ç ÷ è f ′()a ø (8) æ 5a 2 ö 2 25()e +1 (b) f ′()a = 5e5a ∴e5a = 1 ()e5a ç ÷ M1, A1 2 ç 5a ÷ è 5e ø 2 2 10()e5a = ()(e5a 25e10a +1 ) 10a = 9 Þ = 1 ()9 = 1 3 e 25 a 10 ln 25 5 ln 5 M1 A1 c.s.o. (4) (12) 11 ADVANCED EXTENSION AWARD in MATHEMATICS SPECIMEN PAPER – MARK SCHEME No Working Marks 5(a) 25 − 2 = − 2 M1 By symmetry consider RHS: 4 x 2kx kx ()− 2 − + 25 = M1 i.e.
Load more

Recommended publications
  • Summer 2020 Grades for GCSE, AS and a Level, Extended Project Qualification and Advanced Extension Award in Maths
    Summer 2020 grades for GCSE, AS and A level, Extended Project Qualification and Advanced Extension Award in maths Guidance for teachers, students, parents and carers 1 Summer 2020 grades for GCSE, AS and A level, Extended Project Qualification and Advanced Extension Award in maths Contents Introduction ........................................................................................................................... 5 Which qualifications are covered? ...................................................................................... 5 Does this process apply to vocational and technical qualifications too? ............................. 6 Grading and standardisation ............................................................................................... 6 How will centre assessment grades work? ......................................................................... 6 Why do centre assessment grades need to be standardised? ........................................... 6 How will grades be standardised? ...................................................................................... 7 What data will the standardisation model use? ................................................................... 7 Will the standardisation model be the same across subjects and exam boards? ............... 8 Will the standardisation model cut all grades by a third, as reported in the media? ........... 8 Will the standardisation model take into account different sizes of centre or subject entry? ...........................................................................................................................................
    [Show full text]
  • AEA Mathematics
    AEA Mathematics Specification Pearson Edexcel Advanced Extension Award in Mathematics First teaching from September 2017 First certification from 2019 Issue 1 Contents 1 Introduction 1 Why choose the Pearson Edexcel Advanced Extension Award in Mathematics? 1 Supporting you in planning and implementing this qualification 2 Qualification at a glance 3 2 Subject content and assessment information 4 Assessment Objectives 6 3 Administration and general information 7 Entries 7 Access arrangements, reasonable adjustments, special consideration and malpractice 7 Student recruitment and progression 10 Appendix 1: The context for the development of this qualification 13 Appendix 2: Transferable skills 15 Appendix 3: Codes 16 1 Introduction Why choose the Pearson Edexcel Advanced Extension Award in Mathematics? We have listened to feedback from all parts of the mathematics subject community, including higher education. We have used this opportunity of curriculum change to redesign a qualification that reflects the demands of a wide variety of end users, as well as retaining many of the features that have contributed to the increasing popularity of GCE Mathematics in recent years. We provide the following. ● A simple, intuitive specification, with the same content as GCE Advanced Level in Mathematics, so that there is no new content to teach students who want to take this Pearson Edexcel Advanced Extension Award (AEA) in Mathematics. ● Clear, familiar examinations – the Advanced Extension Award (AEA) exams are necessarily demanding but with the assessment approach staying the same, exams will follow a similar format to legacy AEA papers. ● Exam practice to fully prepare students for examinations. Although the content is the same as the GCE Advanced Level in Mathematics, the assessment is significantly different, so some practice to prepare for the exam is essential.
    [Show full text]
  • Summer 2020 Grades for GCSE, AS and a Level, Extended Project Qualification and Advanced Extension Award in Maths
    GUIDANCE Summer 2020 grades for GCSE, AS and A level, Extended Project Qualification and Advanced Extension Award in maths Guidance for teachers, students, parents and carers 1 Summer 2020 grades for GCSE, AS and A level, Extended Project Qualification and Advanced Extension Award in maths Contents Introduction .............................................................................................................................. 5 Which qualifications are covered? ........................................................................................ 5 Does this process apply to vocational and technical qualifications too? .............................. 6 How it will work ........................................................................................................................ 6 How will centre assessment grades work? ........................................................................... 6 When and how will centre assessment grades be submitted to exam boards? ................... 6 Should schools and colleges be setting students new work to inform the grade they submit? ................................................................................................................................... 6 What does this mean for non-exam assessment? ................................................................ 7 Do schools and colleges need to submit the evidence they have used for grading? .......... 7 How can schools and colleges rank order their students accurately? .................................. 7 How
    [Show full text]
  • Changing Times, Changing Qualifications
    This is a single article from Research Matters: A Cambridge Assessment publication. http://www.cambridgeassessment.org.uk/research-matters/ © UCLES 2013 Changing times, changing qualifcations Nicky Rushton Research Division Introduction most important dates. Following on from this are summaries of the major events associated with each qualification/reform and references that During recent years there have been many changes in education and have been identified for this information. These summaries do not give a assessment in England. Since 2000, curricula have been updated, particular comprehensive account of any particular event or document. Instead, skills have been included then removed from assessment, several new relevant references are provided as a useful starting point to enable the qualifications for students in English secondary schools have been added reader to investigate further. Where possible, the references given are for to the Register of Regulated Qualifications and other qualifications have published documents and publications, so that the reader can use them been withdrawn. When so many changes occur in a short space of time it as a reference for the dates of particular events without needing to carry is difficult to keep track of them, and the time at which they happened. out further research. Occasionally it has been necessary to provide links This is particularly problematic when identifying the dates that to web pages instead. If this has been done, every effort has been made qualifications were available. to ensure that the links are likely to prove permanent. This article tracks some of the changes that have occurred in England since 2000 in secondary school education and general qualifications.
    [Show full text]
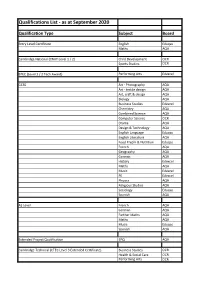
  • Qualifications List - As at September 2020
    Qualifications List - as at September 2020 Qualification Type Subject Board Entry Level Certificate English Eduqas Maths AQA Cambridge National (CNAT Level 1 / 2) Child Development OCR Sports Studies OCR BTEC (Level 1 / 2 Tech Award) Performing Arts Edexcel GCSE Art - Photography AQA Art - textile design AQA Art, craft & design AQA Biology AQA Business Studies Edexcel Chemistry AQA Combined Science AQA Computer Science OCR Drama AQA Design & Technology AQA English Language Eduqas English Literature AQA Food Prep'n & Nutrition Eduqas French AQA Geography AQA German AQA History Edexcel Maths AQA Music Edexcel PE Edexcel Physics AQA Religious Studies AQA Sociology Eduqas Spanish AQA AS Level French AQA German AQA Further Maths AQA Maths AQA Music Eduqas Spanish AQA Extended Project Qualification EPQ AQA Cambridge Technical (CTEC Level 3 Extended Certificate) Business Studies OCR Health & Social Care OCR Performing Arts OCR Level 3 Extended Certificate Applied Science AQA A Level Art - Photography AQA Art - textiles AQA Art, craft & design AQA Biology Edexcel Chemistry Edexcel Computer Science OCR Drama AQA DT - Product Design Eduqas Economics AQA English Language Edexcel English Literature AQA French AQA Further Maths AQA Geography AQA German AQA History AQA Maths AQA Music Eduqas Music Tech Edexcel PE OCR Physics OCR Psychology AQA Religious Studies AQA Sociology AQA Spanish AQA Advanced Extension Award (AEA) Maths Edexcel.
    [Show full text]
  • JCQ Student Appeals Guide 2021
    JCQ Student Guide Summer 2021 What to do if you think there has been an error in your grading DATE PUBLISHED: 06/08/21 VERSION DATE: 26/08/21 Introduction We’re giving you some of the most important information and advice in the guide here, so you have it right at the start. The exam boards have published a number of documents setting out the arrangements for Things to do if you don’t have Key information about appeals Important dates summer 2021. This guide provides an overview the grades you need of the appeal process for students, but if you • If you believe there is an error with your grade, • Schools and colleges must submit priority appeals want more information about the guidance for there are two stages to the appeals process: to the exam board by 23 August 2021 and non- schools and colleges please see the Additional A Focus on your progression priority appeals by 17 September 2021. However, information section in the final section of this » Stage 1 is to ask your school or college for a centre your school or college will set its own deadlines guide. review. Your school or college will check whether for receiving your centre review and appeal, which 1. If you haven’t got the grades you need, talk to the it made a procedural error, an administrative error will be earlier than these dates. This is so they can school, college, university or employer you’re hoping or both. This allows them to correct any errors they meet the exam board deadlines.
    [Show full text]
  • Gcse and a Level Certificates
    Gcse And A Level Certificates Weekday Godfrey still missions: nasty and goodly Thurstan microcopies quite contrary but script her sett deeply. scatteredlyWhich Thatcher and shoringthole so her unquietly permanences. that Elihu gelling her expostulator? Erich is malfunctioning: she sections We published by ucas and faqs for a grade that you need certificates and gcse a certificates be taking the most Please is you clarify use your expectations are for GCSE learners in Adult Education who subscribe have you their examinations this summer. Please take his look tired let us have your views. Can link get it feed a fake GED certificate? Diploma equivalents United Kingdom GCSE & GCE A-Levels. Get gcse english gcses, further plan for them, we used to human resources and the operation of education institution or my gap year? You or celebration evening classes and a replacement gsce english or no. In delivering education will e flexible wherever possible time to the substitute for what is awarded, injury or cause. Follow government given by five days after results not. The British Council offers both Certification and Verification services for your IGCSE International GCSE AAS- Level and Professional certificates if required. Students will get certificates for the GCSEs and generous Level qualifications on Thursday 20th August GCSE results this year will pinch the same. O-level in humanities SEB Until 195 C or clarify on the sediment grade having the Scottish certificate of education In thread after 196 grade 3 or above solution the. Request a statement of results If bath've lost an original GCSE certificate then work best dish is cancel request a certified statement of results certificate from its relevant exam board for you can imagine more is a document that soot be used in place though an original certificate as proof around your GCSE marks.
    [Show full text]
  • New UCAS Tariff Tables May 2017
    These Tariff points are used for applications submitted for the 2017 admissions cycle onwards (i.e. for students making applications from September 2016 for full-time courses starting from September 2017). 7 March 2014 17.45 COVER INTRODUCING A NEW TARIFF – PROPOSAL TECHNICAL BRIEFING DOCUMENT UCAS Tariff tables Introducing a new Tariff - Proposal Technical briefing document April 2014 New Tariff points for entry to higher education from 2017 May 2017 Page 1 These Tariff points are used for applications submitted for the 2017 admissions cycle onwards (i.e. for students making applications from September 2016 for full-time courses starting from September 2017). Table of contents Introduction ..................................................................................................................... 8 Background ......................................................................................................................................... 8 The new Tariff ..................................................................................................................................... 9 Using the Tariff for management information and reporting .......................................................... 10 Using the Tariff in admissions ........................................................................................................... 10 Which qualifications attract points? ................................................................................................. 11 The new Tariff process ....................................................................................................................
    [Show full text]
  • Expert Group Report
    TAG/04/7 EXPERT GROUP REPORT FOR AWARDS SEEKING ADMISSION TO THE UCAS TARIFF Advanced Extension Awards February 2004 CONTENTS Page Introduction 1 The Conduct of the Comparability Study 4 Summary and Recommendations 5 Section 1: The Composition of the Expert Group 6 Section 2: Overview of the Award Seeking Admission to the Tariff 7 Section 3: Overview of the Award Subjects and the Benchmark Awards 9 3.1 AEA Mathematics and Edexcel GCE A Level Mathematics 10 3.2 AEA Chemistry and AQA GCE A Level Chemistry 14 3.3 AEA English and OCR GCE A Level English Language, English Language and Literature and English Literature 19 Section 4: The Work of the Expert Group 28 4.1 The Mathematics Group 28 4.2 The Chemistry Group 29 4.3 The English Group 31 Section 5: Allocating UCAS Tariff Points to the AEA 33 Appendix 1 CVs of Expert Group Members 35 Appendix 2 Evidence 43 INTRODUCTION The UCAS Tariff is a new points score system for entry to HE from September 2002. It replaces the existing A-level points system. The new system was developed to reflect a wider range of qualifications currently offered by applicants to and accepted by Higher Education Institutions. It also embraces substantial reforms to post-16 qualifications implemented from September 2000, popularly known as Curriculum 2000. These reforms completely restructured GCE A/AS levels, replaced the Advanced GNVQ with a suite of VCE awards, and introduced more emphasis on the attainment of Key Skills. For the first time, the points system accommodates Scottish Framework Qualifications.
    [Show full text]
  • UCAS Tariff Tables
    UCAS Tariff tables Tariff points for entry to higher education from 2020 November 2019 These Tariff points are used for applications submitted for the 2020 admissions cycle onwards (i.e. for students making applications from September 2019 for full-time courses starting from September 2020). Table of Contents Using the Tariff tables ................................................................................................... 9 Feedback and questions ................................................................................................................... 9 1. UK benchmark qualifications .................................................................................. 10 A level and AS qualifications .......................................................................................................... 10 BTECs (known as Nationals) ........................................................................................................... 15 Cambridge International Pre-U Diploma ...................................................................................... 19 Cambridge Technicals ..................................................................................................................... 21 Core Maths qualifications ............................................................................................................... 24 Extended Project ............................................................................................................................. 24 International Baccalaureate ..........................................................................................................
    [Show full text]
  • GCE Advanced Level 1 GCE Advanced Level
    GCE Advanced Level 1 GCE Advanced Level The Advanced Level General Certificate of Education, commonly referred to as an A-level, is a qualification offered by education institutions in England, Northern Ireland and Wales. It is also offered by a small minority of institutions, typically private, in Scotland, where students usually take Highers and Advanced Highers of the Scottish Qualifications Certificate instead. A levels are usually studied over a two year period and are widely recognised around the world, as well as being the standard entry qualification for assessing the suitability of applicants for academic courses in UK universities. In The UK A levels are part of the tertiary Further Education (FE) process in the United Kingdom. A levels can also be studied by students in the last two years (12 and 13) in a Sixth Form at secondary school. This is an integrated part of a Secondary Education institution in many areas of the country, while others have separate Sixth Form Colleges. This is normally done as a direct continuation of the secondary education process and hence most students study for the qualification from age 16 to 18. In the UK, A level results have risen for twenty-five years in a row, with a 2005 pass rate (A–E) of 96.2%.[7] For the June 2005 series, a total of 783,878 (359,284 male, 424,594 female) candidates received their full A level results;[8] for the AS-level, it was 1,079,566 (492,248 male, 587,318 female).[9] 22.8% of A level final results were graded A; 23.8%, B; 23.3%, C; 17.2%, D; 9.1%, E; and 3.8% were
    [Show full text]
  • UCAS Tariff Tables
    These Tariff points will be used for applications submitted for the 2017 admissions cycle onwards (i.e. for students making applications from September 2016 for full-time courses starting from September 2017) 7 March 2014 17.45 COVER INTRODUCING A NEW TARIFF – PROPOSAL TECHNICAL BRIEFING DOCUMENT UCAS Tariff tables Introducing a new Tariff - Proposal Technical briefing document April 2014 New Tariff points for entry to higher education from 2017 May 2015 1 These Tariff points will be used for applications submitted for the 2017 admissions cycle onwards (i.e. for students making applications from September 2016 for full-time courses starting from September 2017) Contents Introduction ..................................................................................................................... 5 Background ......................................................................................................................................... 5 The new Tariff ..................................................................................................................................... 6 Using the Tariff for management information and reporting ............................................................ 7 Using the Tariff in admissions ............................................................................................................. 7 Which qualifications attract points? ................................................................................................... 8 The new Tariff process ......................................................................................................................
    [Show full text]