1 Mean Reversion and Market Predictability Jon Exley, Andrew
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Future of Computer Trading in Financial Markets an International Perspective
The Future of Computer Trading in Financial Markets An International Perspective FINAL PROJECT REPORT This Report should be cited as: Foresight: The Future of Computer Trading in Financial Markets (2012) Final Project Report The Government Office for Science, London The Future of Computer Trading in Financial Markets An International Perspective This Report is intended for: Policy makers, legislators, regulators and a wide range of professionals and researchers whose interest relate to computer trading within financial markets. This Report focuses on computer trading from an international perspective, and is not limited to one particular market. Foreword Well functioning financial markets are vital for everyone. They support businesses and growth across the world. They provide important services for investors, from large pension funds to the smallest investors. And they can even affect the long-term security of entire countries. Financial markets are evolving ever faster through interacting forces such as globalisation, changes in geopolitics, competition, evolving regulation and demographic shifts. However, the development of new technology is arguably driving the fastest changes. Technological developments are undoubtedly fuelling many new products and services, and are contributing to the dynamism of financial markets. In particular, high frequency computer-based trading (HFT) has grown in recent years to represent about 30% of equity trading in the UK and possible over 60% in the USA. HFT has many proponents. Its roll-out is contributing to fundamental shifts in market structures being seen across the world and, in turn, these are significantly affecting the fortunes of many market participants. But the relentless rise of HFT and algorithmic trading (AT) has also attracted considerable controversy and opposition. -

Perspectives on the Equity Risk Premium – Siegel
CFA Institute Perspectives on the Equity Risk Premium Author(s): Jeremy J. Siegel Source: Financial Analysts Journal, Vol. 61, No. 6 (Nov. - Dec., 2005), pp. 61-73 Published by: CFA Institute Stable URL: http://www.jstor.org/stable/4480715 Accessed: 04/03/2010 18:01 Your use of the JSTOR archive indicates your acceptance of JSTOR's Terms and Conditions of Use, available at http://www.jstor.org/page/info/about/policies/terms.jsp. JSTOR's Terms and Conditions of Use provides, in part, that unless you have obtained prior permission, you may not download an entire issue of a journal or multiple copies of articles, and you may use content in the JSTOR archive only for your personal, non-commercial use. Please contact the publisher regarding any further use of this work. Publisher contact information may be obtained at http://www.jstor.org/action/showPublisher?publisherCode=cfa. Each copy of any part of a JSTOR transmission must contain the same copyright notice that appears on the screen or printed page of such transmission. JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. CFA Institute is collaborating with JSTOR to digitize, preserve and extend access to Financial Analysts Journal. http://www.jstor.org FINANCIAL ANALYSTS JOURNAL v R ge Perspectives on the Equity Risk Premium JeremyJ. -
Commodities Favored with Mean Reversion
Market Commentary 1 Energy 3 Bloomberg Commodity Index (BCOM) Metals 6 Agriculture 11 Tables & Charts – January 2018 Edition DATA PERFORMANCE: 14 Overview, Commodity TR, Prices, Volatility Commodities Favored With CURVE ANALYSIS: 18 Contango/Backwardation, Roll Yields, Mean Reversion Forwards/Forecasts MARKET FLOWS: 21 Open Interest, Volume, - Commodities hitting stride with weak greenback, inflation & economic growth COT, ETFs - Energy is a bit too hot, agriculture too cold, metals the steady bull - Commodities set to shine when volatility returns to financial markets - Strong precious vs. industrial metals may be anticipating a bit of stock market normalization Gold Outlook 2018 Webinar, February 22, 11: 00 am EST https://platform.cinchcast.com/ses/s6SMtqZXpK0t3tNec9WLoA~~ Mike McGlone – BI Senior Commodity Strategist BI COMD (the commodity dashboard) Mean Reversion, a Potential Key 2018 Commodity Bull Gaining Stride Theme, Favors Commodities Crude to Copper: Commodity Relative-Value Performance: January +2.0%, Spot +1.9%. Foundation Is Firming. Agriculture is favored vs. energy, (Returns are total return (TR) unless noted) at least in the shorter term, with mean-reversion overdue in corn, the commodity with the most net-short positions, (Bloomberg Intelligence) -- The commodity bull market vs. crude oil (the longest). Energy should stabilize, metals should be just hitting its stride. Relative to its primary remain strong, and grains are ripe to advance about a drivers -- a declining dollar, rising inflation, demand third on some weather normalization. exceeding supply and expanding global economic growth -- the Bloomberg Commodity Spot Index's four-year high Commodities should have an advantage in 2018 vs. in January is on the right path. -

There's More to Volatility Than Volume
There's more to volatility than volume L¶aszl¶o Gillemot,1, 2 J. Doyne Farmer,1 and Fabrizio Lillo1, 3 1Santa Fe Institute, 1399 Hyde Park Road, Santa Fe, NM 87501 2Budapest University of Technology and Economics, H-1111 Budapest, Budafoki ut¶ 8, Hungary 3INFM-CNR Unita di Palermo and Dipartimento di Fisica e Tecnologie Relative, Universita di Palermo, Viale delle Scienze, I-90128 Palermo, Italy. It is widely believed that uctuations in transaction volume, as reected in the number of transactions and to a lesser extent their size, are the main cause of clus- tered volatility. Under this view bursts of rapid or slow price di®usion reect bursts of frequent or less frequent trading, which cause both clustered volatility and heavy tails in price returns. We investigate this hypothesis using tick by tick data from the New York and London Stock Exchanges and show that only a small fraction of volatility uctuations are explained in this manner. Clustered volatility is still very strong even if price changes are recorded on intervals in which the total transaction volume or number of transactions is held constant. In addition the distribution of price returns conditioned on volume or transaction frequency being held constant is similar to that in real time, making it clear that neither of these are the principal cause of heavy tails in price returns. We analyze recent results of Ane and Geman (2000) and Gabaix et al. (2003), and discuss the reasons why their conclusions di®er from ours. Based on a cross-sectional analysis we show that the long-memory of volatility is dominated by factors other than transaction frequency or total trading volume. -

Nber Working Paper Series Mean Reversion in Stock Prices: Evidence
NBER WORKING PAPER SERIES MEAN REVERSION IN STOCK PRICES: EVIDENCE AND IMPLICATIONS James M. Poterba Lawrence H. Summers Working Paper No. 2343 NATIONAL BUREAU OF ECONOMIC RESEARCH 1050 Massachusetts Avenue Cambridge, MA 02138 August 1987 We are grateful to Barry Peristein, Changyong Rhee, Jeff Zweibel and especially David Cutler for excellent research assistance, to Ben Bernanke, John Campbell, Robert Engle, Eugene Fama, Pete Kyle, Greg Mankiw, Julio Rotemberg, William Schwert, Kenneth Singleton, and Mark Watson for helpful comments, and to James Darcel, Matthew Shapiro, and Ian Tonks for data assistance. This research was supported by the National Science Foundation and was conducted while the first author was a Batterymarch Fellow. The research reported here is part of the NBERs research program in Financial Markets and Monetary Economics. Any opinions expressed are those of the authors and not those of the National Bureau of Economic Research. NBER Working Paper #2343 August 1987 Mean Reversion in Stock Prices: Evidence and Implications ABSTRACT This paper analyzes the statistical evidence bearing on whether transitory components account for a large fraction of the variance in common stock returns. The first part treats methodological issues involved in testing for transitory return components. It demonstrates that variance ratios are among the most powerful tests for detecting mean reversion in stock prices, but that they have little power against the principal interesting alternatives to the random walk hypothesis. The second part applies variance ratio tests to market returns for the United States over the 1871-1986 period and for seventeen other countries over the 1957-1985 period, as well as to returns on individual firms over the 1926- 1985 period. -
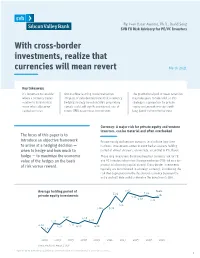
With Cross-Border Investments, Realize That Currencies Will Mean Revert March 2021
By: Ivan Oscar Asensio, Ph.D., David Song SVB FX Risk Advisory for PE/VC Investors With cross-border investments, realize that currencies will mean revert March 2021 Key takeaways It’s important to consider Our machine learning model trained on The gravitational pull of mean reversion where a currency trades 30 years of data demonstrates that a currency may take years to take hold, so this relative to its historical hedging strategy based on SVB’s proprietary strategy is appropriate for private mean when allocating signals could add significant internal rate of equity and growth investors with capital overseas. return (IRR) to overseas investments. long-dated investment horizons. Currency: A major risk for private equity and venture investors, can be material and often overlooked The focus of this paper is to introduce an objective framework Private equity and venture investors tend to have long time to arrive at a hedging decision — horizons. Investments exited in 2019 had an average holding when to hedge and how much to period of almost six years, on average, according to Pitchbook. hedge — to maximize the economic Those long investment durations heighten currency risk for PE value of the hedges on the basis and VC investors who inherit foreign exchange (FX) risk as a by- of risk versus reward. product of allocating capital abroad. Cross-border investments typically are denominated in a foreign currency1, introducing the risk that depreciation in the destination currency between the entry and exit date could undermine the investment’s IRR. 6.02 Years Average holding period of 5.84 5.82 5.76 private equity investments 5.91 5.80 5.75 5.47 5.04 5.31 4.52 4.45 4.33 4.27 4.34 4.07 4.23 4.29 4.26 3.77 2001 2003 2005 2007 2009 2011 2013 2015 2017 2019 Source: Pitchbook, August 1, 2019 1 Applies when both the acquisition and the exit price are denominated in a foreign currency. -

2 Exploiting Mean Reversion
CITI PRIVATE BANK OUTLOOK 2021 27 2 Exploiting mean reversion CONTENTS 2.1 Reversion to the mean and what it means for portfolios 2.2 Capitalize on distressed opportunities INVESTMENT PRODUCTS: NOT FDIC INSURED · NOT CDIC INSURED · NOT GOVERNMENT INSURED · NO BANK GUARANTEE · MAY LOSE VALUE CITI PRIVATE BANK EXPLOITING MEAN REVERSION OUTLOOK 2021 28 2.1 Reversion to the mean and what it means for portfolios STEVEN WIETING - Chief Investment Strategist and Chief Economist JOSEPH FIORICA - Head of Global Equity Strategy KRIS XIPPOLITOS - Head of Global Fixed Income Strategy The arrival of the worst global pandemic in more than a century moved every asset price in the world, and its departure will do the same. It is time to position portfolios to exploit what comes next. COVID-19 has caused huge economic and financial market disruption, but it is neither unstoppable nor a trend Instead, we believe the pandemic’s impacts are temporary, causing massive valuation distortions in 2020 that will unwind in 2021 Many asset prices and relationships between assets have strayed far from their long-term relationships Just as COVID moved every asset price in the world, the same will occur as it departs We expect a “reversion to the mean,” in which certain sectors will be major beneficiaries These include COVID-cyclical sectors, small-cap equities and some of the most beaten-down national and regional markets After the most significant dispersion of asset prices in history, exploiting this mean reversion will be crucial to your portfolio’s return opportunities in 2021 CITI PRIVATE BANK EXPLOITING MEAN REVERSION OUTLOOK 2021 29 COVID-19 has split the world’s companies prices for 2021. -

U.S. Equity Mean-Reversion Examined
Risks 2013, 1, 162-175; doi:10.3390/risks1030162 OPEN ACCESS risks ISSN 2227-9091 www.mdpi.com/journal/risks Article U.S. Equity Mean-Reversion Examined Jim Liew * and Ryan Roberts Johns Hopkins Carey Business School 100 International Drive, Office 1355, Baltimore, Maryland, 21202, USA * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +1-410-234-9401. Received: 16 October 2013; in revised form: 13 November 2013 / Accepted: 18 November 2013 / Published: 4 December 2013 Abstract: In this paper we introduce an intra-sector dynamic trading strategy that captures mean-reversion opportunities across liquid U.S. stocks. Our strategy combines the Avellaneda and Lee methodology (AL; Quant. Financ. 2010, 10, 761–782) within the Black and Litterman framework (BL; J. Fixed Income, 1991, 1, 7–18; Financ. Anal. J. 1992, 48, 28–43). In particular, we incorporate the s-scores and the conditional mean returns from the Orstein and Ulhembeck (Phys. Rev. 1930, 36, 823–841) process into BL. We find that our combined strategy ALBL has generated a 45% increase in Sharpe Ratio when compared to the uncombined AL strategy over the period from January 2, 2001 to May 27, 2010. These new indices, built to capture dynamic trading strategies, will definitely be an interesting addition to the growing hedge fund index offerings. This paper introduces our first “focused-core” strategy, namely, U.S. Equity Mean-Reversion. Keywords: Black–Litterman; US stocks; dynamic trading strategy; mean-reversion; quantitative finance; statistical arbitrage 1. Background Recently, we have seen a proliferation of hedge fund replication products. -

Smart Beta and the Pendulum of Mispricing by Vitali Kalesnik, Ph.D
SIMPLYSTATED September 2013 Smart Beta and the Pendulum of Mispricing by Vitali Kalesnik, Ph.D. Stock price movements aren’t as smooth and steady as a pendulum’s arc, but they both exhibit a process of long-run mean reversion. Highs and lows are temporary; prices tend to return to more average levels. Vitali Kalesnik reviews empirical findings on mean reversion in stock prices, discusses its links with the value and small size premia, and considers why arbitrage doesn’t curtail the process. Through rebalancing, he says, Smart Beta can profit from mean reversion. The Research Affiliates approach to equity investment the bob’s average position, it is the place where we are management is based upon the insight that stock prices most likely to find the bob in the long run. The shorter are “noisy” and “mean-reverting.” and shorter swings of the bob constitute the process of reverting to the mean. • Noisy. Calling prices “noisy” means acknowledging that they contain errors. The market overvalues A pendulum is, of course, governed by Newtonian some stocks and undervalues others. Investors who mechanics and has few irregularities. In contrast, the buy and sell stocks irrationally or erratically are process of mean reversion in financial markets is neither known as “noise traders.” deterministic nor smooth. Nonetheless, the pendulum analogy expresses key characteristics of stock price • Mean-reverting. “Mean reversion” means that stocks movements. whose prices have been trending upward or downward will, at some point, reverse direction and In the short run the most recent price movements are head back toward their average values. -

Arxiv:1705.08022V1
Using Macroeconomic Forecasts to Improve Mean Reverting Trading Strategies Yash Sharma Abstract A large class of trading strategies focus on opportunities offered by the yield curve. In partic- ular, a set of yield curve trading strategies are based on the view that the yield curve mean- reverts. Based on these strategies’ positive performance, a multiple pairs trading strategy on ma- jor currency pairs was implemented. To improve the algorithm’s performance, machine learning forecasts of a series of pertinent macroeconomic variables were factored in, by optimizing the weights of the trading signals. This resulted in a clear improvement in the APR over the evalua- tion period, demonstrating that macroeconomic indicators, not only technical indicators, should be considered in trading strategies. 1. Yield Curve The Yield Curve is a line that plots the interest rate, at a set point in time, of bonds having equal credit quality but differing maturity dates. The U.S. Treasury Yield Curve is used as a benchmark for other debt in the market, and can also be used to predict changes in economic output and growth. The shape of the yield curve gives an idea of future interest rate changes and economic activity. An inverted yield curve is often a harbinger of recession. A positively sloped yield curve is often a harbinger of inflationary growth. These predictive properties make the yield curve quite applicable in devising successful trading strategies. Many yield curve trading strategies are based on the conventional view that the yield curve mean-reverts to some historical norm. This market view is consistent with historical experience. -

Market Making and Mean Reversion
University of Pennsylvania ScholarlyCommons Departmental Papers (CIS) Department of Computer & Information Science 6-2011 Market Making and Mean Reversion Tanmoy Chakraborty University of Pennsylvania Michael J. Kearns University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/cis_papers Part of the Computer Sciences Commons Recommended Citation Tanmoy Chakraborty and Michael J. Kearns, "Market Making and Mean Reversion", . June 2011. Chakraborty, T. & Kearns, M., Market Making and Mean Reversion, 12th ACM Conference on Electronic Commerce, June 2011, doi: 10.1145/1993574.1993622 ACM COPYRIGHT NOTICE. Copyright © 2011 by the Association for Computing Machinery, Inc. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a ee.f Request permissions from Publications Dept., ACM, Inc., fax +1 (212) 869-0481, or [email protected]. This paper is posted at ScholarlyCommons. https://repository.upenn.edu/cis_papers/643 For more information, please contact [email protected]. Market Making and Mean Reversion Abstract Market making refers broadly to trading strategies that seek to profit yb providing liquidity to other traders, while avoiding accumulating a large net position in a stock. -

Statistical Arbitrage with Mean-Reverting Overnight Price Gaps on High-Frequency Data of the S&P
Journal of Risk and Financial Management Article Statistical Arbitrage with Mean-Reverting Overnight Price Gaps on High-Frequency Data of the S&P 500 Johannes Stübinger * and Lucas Schneider Department of Statistics and Econometrics, University of Erlangen-Nürnberg, Lange Gasse 20, 90403 Nürnberg, Germany; [email protected] * Correspondence: [email protected] Received: 27 February 2019; Accepted: 26 March 2019; Published: 1 April 2019 Abstract: This paper develops a fully-fledged statistical arbitrage strategy based on a mean-reverting jump–diffusion model and applies it to high-frequency data of the S&P 500 constituents from January 1998–December 2015. In particular, the established stock selection and trading framework identifies overnight price gaps based on an advanced jump test procedure and exploits temporary market anomalies during the first minutes of a trading day. The existence of the assumed mean-reverting property is confirmed by a preliminary analysis of the S&P 500 index; this characteristic is particularly significant 120 min after market opening. In the empirical back-testing study, the strategy delivers statistically- and economically-significant returns of 51.47 percent p.a.and an annualized Sharpe ratio of 2.38 after transaction costs. We benchmarked our trading algorithm against existing quantitative strategies from the same research area and found its performance superior in a multitude of risk-return characteristics. Finally, a deep dive analysis shows that our results are consistently profitable and robust against drawdowns, even in recent years. Keywords: computational finance; asset pricing models; overnight price gaps; financial econometrics; mean-reversion; statistical arbitrage; high-frequency data; jump-diffusion model 1.