Lesson 5: Transcript.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Village of Hastings-On-Hudson, New York Zoning Board of Appeals Regular Meeting April 27, 2017
VILLAGE OF HASTINGS-ON-HUDSON, NEW YORK ZONING BOARD OF APPEALS REGULAR MEETING APRIL 27, 2017 A Regular Meeting was held by the Zoning Board of Appeals on Thursday, April 27, 2017 at 8:00 p.m. in the Meeting Room, Municipal Building, 7 Maple Avenue. PRESENT: Chairman Matthew Collins, Boardmember Ray Dovell, Boardmember David Forbes-Watkins, Boardmember Sean Hayes, Alternate Boardmember Denise Wagner Furman, Village Counsel Seth Mandelbaum, and Building Inspector Charles Minozzi, Jr. Chairman Collins: OK, why don't we begin? Thank you for joining us for the April 27 meeting of the Zoning Board of Appeals. Case No. 9-17 Dean & Marie Wetherell 196 Warburton Avenue ***Deferred to Future Meeting*** For View Preservation approval, as required under Village Code Section 29582 and relief from the strict application of Sections 29568E & 29568F.2.a.2, for the creation of two (2) nonconforming lots and a new proposed single family- dwelling on their property at 196 Warburton Avenue. Said property is located in the R10 Zoning District and is known as SBL: 4.13013917&18 on the Village Tax Maps. Nonconformity details of the subdivision and proposed construction are as follows: Lot width: Proposed - 65.76 feet avg. (Lot #1) & 79.09 feet average; (Lot #2) - Required; 100 feet (each) {29568.E.}; Variance Required - 34.24 feet (Lot #1) & 20.91 feet (Lot #2) Developmental Coverage (Lot #2): Proposed - 36.35%; Required - Maximum 35 percent {29568.F.2 (a.2)}; Variance Required - 1.35 percent Chairman Collins: We have only one active case on the docket this evening. We also have a separate agenda item, which I'm going to push 'til after this application, given the way I expect this to proceed. -

Issue Commenter Does This Issue Relate to Resolving Adverse Effect?
Summary of issues raised by interested parties and the public when asked for ideas to resolve the direct adverse effect of Forest Service requiring removal of the Wolf Creek Boatworks (6/16/2020) Does this Issue relate to resolving adverse Issue Commenter effect? Forest Service Note 11 commenters requested that the Boatworks be C, J, K, L, M, Yes Because the Forest Service does not own the preserved. N, O, P, Q, Boatworks improvements, it is not within the R, S authority of the Forest Service to direct that the Boatworks be transferred intact. See Boatworks Overview for additional information relevant to this issue. 10 commenters requested that the Forest Service B,C,E,G,H,K, Yes This proposal is outside the scope of the Forest or Alaska Mental Health Trust Authority (AMHTA) L,M,O,P Service’s authority. See Boatworks Overview for sell or trade the parcel to Mr. Romey or carve the additional information relevant to this issue. parcel out of the Alaska Mental Health Trust (AMHT) Land Exchange Act of 2017. 4 commenters shared their opinion that a kiosk is L,M,P,S Yes The kiosk is an existing mitigation measure in the an insufficient mitigation measure. current programmatic agreement, which is intended to share the overall history of cultural resources types across the island. 1 commenter suggested a historic preservation M Yes There is no provision in the AMHT Land Exchange easement as a mitigation measure. Act of 2017 to encumber the property with an easement. See Boatworks Overview 'Land Exchange Act' section for additional information relevant to this issue. -

May 27, 2020 Zoning Board of Appeals Meeting Over the Internet, Accessible to the General Public Through the Zoom Video Conferencing Platform
Zoning Board of Appeals TOWN OF BRUNSWICK 336 Town Office Road Troy, New York 12180 TRANSCRIPT OF THE BRUNSWICK ZONING BOARD OF APPEALS SPECIAL MEETING HELD MAY 27, 2020 PRESENT were ANN CLEMENTE, CHAIRPERSON, MARTIN STEINBACH, E. JOHN SCHMIDT, WILLIAM SHOVER, and PATRICIA CURRAN. ALSO PRESENT was CHARLES GOLDEN, Brunswick Building Department. Pat Poleto: Good evening, everyone. How’s everyone tonight? Ann, are you here? Chair Clemente: Hi, Pat. Yes. Pat Poleto: Well it’s almost 6:00. Why don’t we go over a couple ground rules before we get going here? We still got people coming, but…OK so this is going to the special Board meeting for the Zoning Board of Appeals for Wednesday, May 27, 2020. Can everybody see the message I have up there? OK. Let’s go over a few rules and we can get going here. So we are recording this on Zoom tonight. This is Pat, I’m the moderator. When you talk, please state your name. If you’re a Board member, say you’re a Board member, consultant, or who you’re representing please. Because we’re going to have to get a transcript of this and so with a person doing the transcript, we’ll need to know who is talking. Sounds a little weird at first but before you start talking, please state your name. OK. And so to make this run smooth with as little technical difficulty as possible, if you’re not talking please mute your audio so we don’t hear everybody’s background and stuff like that. -

8123 Songs, 21 Days, 63.83 GB
Page 1 of 247 Music 8123 songs, 21 days, 63.83 GB Name Artist The A Team Ed Sheeran A-List (Radio Edit) XMIXR Sisqo feat. Waka Flocka Flame A.D.I.D.A.S. (Clean Edit) Killer Mike ft Big Boi Aaroma (Bonus Version) Pru About A Girl The Academy Is... About The Money (Radio Edit) XMIXR T.I. feat. Young Thug About The Money (Remix) (Radio Edit) XMIXR T.I. feat. Young Thug, Lil Wayne & Jeezy About Us [Pop Edit] Brooke Hogan ft. Paul Wall Absolute Zero (Radio Edit) XMIXR Stone Sour Absolutely (Story Of A Girl) Ninedays Absolution Calling (Radio Edit) XMIXR Incubus Acapella Karmin Acapella Kelis Acapella (Radio Edit) XMIXR Karmin Accidentally in Love Counting Crows According To You (Top 40 Edit) Orianthi Act Right (Promo Only Clean Edit) Yo Gotti Feat. Young Jeezy & YG Act Right (Radio Edit) XMIXR Yo Gotti ft Jeezy & YG Actin Crazy (Radio Edit) XMIXR Action Bronson Actin' Up (Clean) Wale & Meek Mill f./French Montana Actin' Up (Radio Edit) XMIXR Wale & Meek Mill ft French Montana Action Man Hafdís Huld Addicted Ace Young Addicted Enrique Iglsias Addicted Saving abel Addicted Simple Plan Addicted To Bass Puretone Addicted To Pain (Radio Edit) XMIXR Alter Bridge Addicted To You (Radio Edit) XMIXR Avicii Addiction Ryan Leslie Feat. Cassie & Fabolous Music Page 2 of 247 Name Artist Addresses (Radio Edit) XMIXR T.I. Adore You (Radio Edit) XMIXR Miley Cyrus Adorn Miguel Adorn Miguel Adorn (Radio Edit) XMIXR Miguel Adorn (Remix) Miguel f./Wiz Khalifa Adorn (Remix) (Radio Edit) XMIXR Miguel ft Wiz Khalifa Adrenaline (Radio Edit) XMIXR Shinedown Adrienne Calling, The Adult Swim (Radio Edit) XMIXR DJ Spinking feat. -
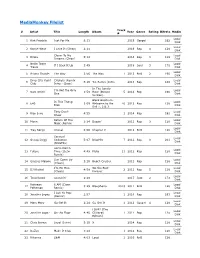
Mediamonkey Filelist
MediaMonkey Filelist Track # Artist Title Length Album Year Genre Rating Bitrate Media # Local 1 Kirk Franklin Just For Me 5:11 2019 Gospel 182 Disk Local 2 Kanye West I Love It (Clean) 2:11 2019 Rap 4 128 Disk Closer To My Local 3 Drake 5:14 2014 Rap 3 128 Dreams (Clean) Disk Nellie Tager Local 4 If I Back It Up 3:49 2018 Soul 3 172 Travis Disk Local 5 Ariana Grande The Way 3:56 The Way 1 2013 RnB 2 190 Disk Drop City Yacht Crickets (Remix Local 6 5:16 T.I. Remix (Intro 2013 Rap 128 Club Intro - Clean) Disk In The Lonely I'm Not the Only Local 7 Sam Smith 3:59 Hour (Deluxe 5 2014 Pop 190 One Disk Version) Block Brochure: In This Thang Local 8 E40 3:09 Welcome to the 16 2012 Rap 128 Breh Disk Soil 1, 2 & 3 They Don't Local 9 Rico Love 4:55 1 2014 Rap 182 Know Disk Return Of The Local 10 Mann 3:34 Buzzin' 2011 Rap 3 128 Macc (Remix) Disk Local 11 Trey Songz Unusal 4:00 Chapter V 2012 RnB 128 Disk Sensual Local 12 Snoop Dogg Seduction 5:07 BlissMix 7 2012 Rap 0 201 Disk (BlissMix) Same Damn Local 13 Future Time (Clean 4:49 Pluto 11 2012 Rap 128 Disk Remix) Sun Come Up Local 14 Glasses Malone 3:20 Beach Cruiser 2011 Rap 128 (Clean) Disk I'm On One We the Best Local 15 DJ Khaled 4:59 2 2011 Rap 5 128 (Clean) Forever Disk Local 16 Tessellated Searchin' 2:29 2017 Jazz 2 173 Disk Rahsaan 6 AM (Clean Local 17 3:29 Bleuphoria 2813 2011 RnB 128 Patterson Remix) Disk I Luh Ya Papi Local 18 Jennifer Lopez 2:57 1 2014 Rap 193 (Remix) Disk Local 19 Mary Mary Go Get It 2:24 Go Get It 1 2012 Gospel 4 128 Disk LOVE? [The Local 20 Jennifer Lopez On the -

ED439138.Pdf
DOCUMENT RESUME ED 439 138 TM 030 672 AUTHOR Wolf, Shelby; Borko, Hilda; McIver,Monette; Elliott, Rebekah TITLE "No Excuses": School Reform Effortsin Exemplary Schools of Kentucky. INSTITUTION Center for Research on Evaluation,Standards, and Student Testing, Los Angeles, CA. SPONS AGENCY Office of Educational Research andImprovement (ED), Washington, DC. REPORT NO CSE-TR-514 PUB DATE 1999-12-00 NOTE 21p. CONTRACT R305B60002 PUB TYPE Reports Evaluative (142) EDRS PRICE MF01/PC01 Plus Postage. DESCRIPTORS *Case Studies; *Cooperation; *Educational Change; Educational Environment; Elementary Education; Middle Schools; *Teacher Attitudes; Teachers IDENTIFIERS *Exemplary Schools; Kentucky; *Kentucky Education Reform Act 1990; Reform Efforts ABSTRACT This report follows two elementary and two middle schools in Kentucky where educators not only talked about what they needed to do to meet the needs of the state's educational reform program, but also acted on their ideas, creating a "no excuses" atmosphere. Images of reform suggest that resource decisions are often based on human relationships among faculty members, and that these, in turn, influence the desire to go out into the community to get what is needed to propel learning forward. These schools characterized themselves as "lighthouses" and "universities" where ongoing learning was key. However, the business side of things was less critical than the emphasis on "family." The report demonstrates how four different exemplary schools took on the question of "What is it we need to do?" and formed a shared vision through their dedication to students, staff, faculty, and school. (SLD) Reproductions supplied by EDRS are the best that can be made from the original document. -

Tangential Heave Stress Acting on Deep Foundations in Cold Regions
Tangential Heave Stress acting on Deep Foundations in Cold Regions Hoyoung Seo, Ph.D., P.E. Liang Li, Graduate Research Assistant William D. Lawson, P.E., Ph.D. Priyantha W. Jayawickrama, Ph.D. SPTC15.1-17-F Southern Plains Transportation Center 201 Stephenson Parkway, Suite 4200 The University of Oklahoma Norman, Oklahoma 73019 DISCLAIMER The contents of this report reflect the views of the authors, who are responsible for the facts and accuracy of the information presented herein. This document is disseminated under the sponsorship of the Department of Transportation University Transportation Centers Program, in the interest of information exchange. The U.S. Government assumes no liability for the contents or use thereof. i TECHNICAL REPORT DOCUMENTATION PAGE 1. REPORT NO. 2. GOVERNMENT ACCESSION NO. 3. RECIPIENTS CATALOG NO. SPTC15.1-17-F 4. TITLE AND SUBTITLE 5. REPORT DATE Tangential Heave Stress Acting on Deep Foundations in May 01 2019 Cold Regions 6. PERFORMING ORGANIZATION CODE 7. AUTHOR(S) 8. PERFORMING ORGANIZATION REPORT Hoyoung Seo, Liang Li, William D. Lawson, and Priyantha W. Jayawickrama 9. PERFORMING ORGANIZATION NAME AND ADDRESS 10. WORK UNIT NO. Texas Tech Center for Multidisciplinary Research in Transportation 11. CONTRACT OR GRANT NO. Texas Tech University DTRT13-G-UTC36 Box 41023 Lubbock, Texas 79409 12. SPONSORING AGENCY NAME AND ADDRESS 13. TYPE OF REPORT AND PERIOD COVERED Southern Plains Transportation Center Final 201 Stephenson Pkwy, Suite 4200 June 2016 – May 2019 The University of Oklahoma 14. SPONSORING AGENCY CODE Norman, OK 73019 15. SUPPLEMENTARY NOTES University Transportation Center 16. ABSTRACT In this study, the research team performed an experimental investigation of the effect of frost heave during soil freezing on the development of tangential heave force acting on deep foundations. -

Next Gen 2019 Leadership Summit
NEXT GEN 2019 LEADERSHIP SUMMIT PROGRAM PARTICIPANTS NEXT GEN 2019LEADERSHIP SUMMIT ERNESTO ALVARENGA Carpet One Floor & Home of Central Florida Celebration, FL TELL US A LITTLE BIT ABOUT YOUR DAILY RESPONSIBILITIES. I’m an owner, my duties pretty much run from supervising to all the background work behind the scenes. WHO IS SOMEONE YOU ADMIRE AND WHY? This is hard to say because I don’t persay admire one person but I take qualities from everyone I meet. TELL US WHAT YOUR THEME SONG WOULD BE. Alright WHAT WAS YOUR FIRST JOB? Pharmacy Tech WHAT WOULD BE YOUR PERSONAL MOTTO OR WHAT IS YOUR FAVORITE QUOTE? Tell me who you hang with and I’ll tell you who you are. NEXT GEN 2019LEADERSHIP SUMMIT MATT ANDREWS Allwein Carpet One Floor & Home Annville, PA TELL US A LITTLE BIT ABOUT YOUR DAILY RESPONSIBILITIES. It starts with getting the installers outfitted and moving in the morning. Then my days vary. I handle our commercial jobs, both main street and bid work. So depending on the day, working on plans, measuring, meeting with clients, reps, etc. Just recently I also took on the measuring and installation of the Hunter Douglas blinds. Other than that, I share the normal duties of an owner with my wife Lauren. Building maintenance, overseeing scheduling, sales, warehouse, etc. WHO IS SOMEONE YOU ADMIRE AND WHY? My Dad. For starters he is genuine. He’s the same guy all the time. He is generous. He constantly gives of his time and resources. That generosity stems from his faith and his big heart. -

The New Set-Up in the Bel Grade Low-Level and Cos Mic-Ray Lab O Ra Tory
A. Dragi}, et al.: The New Set-up in the Bel grade Low-Level and Cos mic-Ray ... Nuclea r Technol ogy & Ra dia tion Pro tection: Year 2011, Vol. 26, No. 3, pp.181-192 181 THE NEW SET-UP IN THE BELGR ADE LOW-LEVEL AND COS MIC-RAY LAB O RA TORY by Aleksandar DRAGI]1*, Vladi mir I. UDOVI^I]1, Radomir BANJANAC1, Dejan JOKOVI]1, Dimitrije MALETI]1, Nikola VESELINOVI]1, Mihailo SAVI]2, Jovan PUZOVI]2, and Ivan V. ANI^IN1 1In sti tute of Phys ics, Bel grade, Ser bia 2Fac ulty of Phys ics, Uni ver sity of Bel grade, Bel grade, Ser bia Sci en tific pa per UDC: 543.428/.429:551.521.6:539.166 DOI: 10.2298/NTRP1103181D The Bel grade un der ground lab o ra tory con sists of two in tercon nected spaces, a ground level labo ra tory and a shal low under ground one, at 25 me ters of wa ter equivalent. The labo ra tory hosts a low-back ground gamma spectros copy sys tem and cos mic-ray muon de tec tors. With the re cently adopted dig i tal data ac qui si tion sys tem it is pos si ble to si mul ta neously study in - de pend ent op er a tions of the two de tec tor sys tems, as well as pro cesses in duced by cos mic-ray muons in ger ma nium spec trom e ters. Char ac ter is tics and po ten tials of the pres ent ex per i men - tal setup, to gether with some pre lim i nary re sults for the flux of fast neu trons and stopped muons, are re ported here. -

Syllabus for FINC303
College of Charleston FINC-303-05 and 10, Business Finance, Course Syllabus Fall 2018 Instructor: Hao-Chen Liu Office/Phone/E-mail: J.C. LONG 307 / 953-1988 / [email protected] Class Time and classroom: Section 05: Tate Center 131, 8:00 a.m. to 9:15 a.m., Tuesdays and Thursdays Section 10: Tate Center 131, 1:40 p.m. to 2:55 p.m., Tuesdays and Thursdays Office Hours: 10:30 a.m. to 12 p.m. on Mondays; 3 p.m. to 4 p.m. on Tuesdays and Thursdays, or by appointment Course Description This course presents the fundamental concepts of corporate finance. Special attention will be given to the financial administrator’s role in the area of working capital, capital budgeting, and financing decisions, including international investment and financial considerations. Recommended Textbook Lessons about the Structure of Finance by Thomas Downs, Pearson Custom Publishing, 8th Edition. The eBook can be purchased online at https://www.bvtstudents.com/3034?filter_name=978-1-62751-667-9 Prerequisites Junior standing; ACCT 203, 204, ECON 200, 201, MATH 104 or 250, DSCI 232 suggested. Learning Goals The goals of this course are for you to learn financial concepts and tools so that you may use finance to analyze financial issues and make financial decisions. You will possess quantitative skills, be aware of important ethical issues in finance, and know the following when you finish this course: (1) To know the goal of financial management and the basic decisions made by financial managers (2) To analyze financial statements and cash flows (3) To use discounted cash flows for stock and bond valuation (4) To use alternative methods for making capital budgeting decisions (5) To calculate risk and return of investment and create a diversified portfolio (6) To estimate company’s cost of capital Calculator & Rounding Policy You will need a financial calculator to succeed in this course. -

Short Story 2020-2021
That One Summer Neda Ravandi 2/24/2021 It all started with David Redford’s goldfish and the dead body. Davey, ever the patriot, had named him John Fitzgerald, and after six long years of friendship it was decided that a death by toilet would not do him justice, so after hastily written notes were left on our respective kitchen counters, we packed baloney sandwiches, shovels, and a small shoebox in a picnic basket and made the mile-long trek out of town. The girls wore our nicest summer dresses, with long, silk hair ribbons, and the boys wore overalls; it was assumed they’d do the tedious work of digging John Fitzgerald’s grave. The funeral was a somber event, and Davey used up many tissues. It was hot that day, sun beating down on our backs through the thin cotton of our summer clothes, and the ceremony lasted for about fifteen minutes before we grew drowsy with summer warmth and sat down on the grass. After a respectful period of time, during which Davey’s grief had lessened, his brother looked at us. “Didja hear about the murder?” “The murder?” “Mr. Miller,” Robbie said solemnly. “Sheriff Johnson found his body all messed up in the cornfields.” Murder rarely happened around here, so we perked up at his words. I wondered aloud if I’d be allowed to write about the case in the Council Grove Republican, but Maggie shrugged. “Well it’s not much of a mystery, is it? There’s no case for solvin’ if everyone knows who did it.” Jamie Flynn was an enigma; rumors hung around him like flies. -

Sweet 16 Hot List
Sweet 16 Hot List Song Artist Happy Pharrell Best Day of My Life American Authors Run Run Run Talk Dirty to Me Jason Derulo Timber Pitbull Demons & Radioactive Imagine Dragons Dark Horse Katy Perry Find You Zedd Pumping Blood NoNoNo Animals Martin Garrix Empire State of Mind Jay Z The Monster Eminem Blurred Lines We found Love Rihanna/Calvin Love Me Again John Newman Dare You Hardwell Don't Say Goodnight Hot Chella Rae All Night Icona Pop Wild Heart The Vamps Tennis Court & Royals Lorde Songs by Coldplay Counting Stars One Republic Get Lucky Daft punk Sexy Back Justin Timberland Ain't it Fun Paramore City of Angels 30 Seconds Walking on a Dream Empire of the Sun If I loose Myself One Republic (w/Allesso mix) Every Teardrop is a Waterfall mix Coldplay & Swedish Mafia Hey Ho The Lumineers Turbulence Laidback Luke Steve Aoki Lil Jon Pursuit of Happiness Steve Aoki Heads will roll Yeah yeah yeah's A-trak remix Mercy Kanye West Crazy in love Beyonce and Jay-z Pop that Rick Ross, Lil Wayne, Drake Reason Nervo & Hook N Sling All night longer Sammy Adams Timber Ke$ha, Pitbull Alive Krewella Teach me how to dougie Cali Swag District Aye ladies Travis Porter #GETITRIGHT Miley Cyrus We can't stop Miley Cyrus Lip gloss Lil mama Turn down for what Laidback Luke Get low Lil Jon Shots LMFAO We found love Rihanna Hypnotize Biggie Smalls Scream and Shout Cupid Shuffle Wobble Hips Don’t Lie Sexy and I know it International Love Whistle Best Love Song Chris Brown Single Ladies Danza Kuduro Can’t Hold Us Kiss You One direction Don’t You worry Child Don’t