DOCSLIB.ORG

Measuring the Magnetization of a Permanent Magnet B

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Measuring the Magnetization of a Permanent Magnet B Measuring the magnetization of a permanent magnet B. Barman Department of Computer Science, Engineering and Physics, University of Michigan-Flint, Flint, Michigan 48502 A. Petrou Department of Physics, University at Buffalo, The State University of New York, Buffalo, New York 14260 (Received 1 July 2018; accepted 10 February 2019) The effect of an external magnetic field B on magnetic materials is a subject of immense importance. The simplest and oldest manifestation of such effects is the behavior of the magnetic compass. Magnetization M plays a key role in studying the response of magnetic materials to B. In this paper, an experimental technique for the determination of M of a permanent magnet will be presented. The proposed method discusses the effect of B (produced by a pair of Helmholtz coils) on a permanent magnet, suspended by two strings and allowed to oscillate under the influence of the torque that the magnetic field exerts on the magnet. The arrangement used Newton’s second law for rotational motion to measure M via graphical analysis. VC 2019 American Association of Physics Teachers. https://doi.org/10.1119/1.5092452 1,5–7 I. INTRODUCTION of the loop. The magnitude l is given by the following equation: Magnetism has been intriguing mankind for centuries now. A magnet’s ability to influence magnetic materials, l ¼ iA: (1) from a distance, mesmerized numerous inquisitive minds of the past. The magnetic compass, used across all continents, If we place this loop in a uniform magnetic field B~ at an is such a device, acting under the influence of Earth’s mag- angle h with ~l, as shown in Fig. 1(a), we have a torque act- netic field.1 With the advancement of science, particularly ing on the loop whose magnitude s is given by the following after the discovery of the atomic model, magnetism at the equation: microscopic scale came to the fore. Hans-Christian Oersted’s discovery of a current-carrying wire producing a magnetic s ¼ lB sin h: (2) field added a whole new dimension, leading to the advent of a technological revolution in the field of electromagnetism.2 If the loop is allowed to move, it will rotate under the action With the exploration of newer magnetic materials, exhibiting of the torque in such a way that ~l becomes parallel with the ~ paramagnetism, ferromagnetism, and diamagnetism, it magnetic field B, as shown in Fig. 1(b). Indeed, in the config- became essential to develop techniques to measure magneti- uration of Fig. 1(b), we have that h ¼ 0 for which Eq. (2) zation in these. While many experimental methods have shows that s ¼ 0 and all movement stops. Thus, the mag- been proposed, along with the existence of high tech equip- netic moment is defined so that the torque exerted on a cur- rent carrying loop, when placed in an external magnetic ment for research, a basic design requirement for educational 8 purposes has eluded us so far.3,4 In this paper, we present an field, is proportional to l. experimental technique to determine the magnetization of a permanent magnet using readily available lab instruments B. Magnetization namely as a pair of Helmholtz coils, an ammeter, a power For our experimental discussion, we consider a cylindrical supply, and a stopwatch. While this technique is applicable permanent magnet (composed of iron atoms) of radius R and for both introductory physics (calculus and algebra based) and height l, as shown in Fig. 2. In each atom, its electrons move undergraduate Physics/Engineering majors, the extent of around the nucleus on orbits similar to that shown in Fig. 1. exploration rests with the instructor. As a quick in-class Thus, each iron atom behaves like a microscopic loop with demo, an introductory class can observe the effect of an exter- magnetic moment ~lFe. In iron and other ferromagnetic mate- nal magnetic field on the oscillation period of a permanent rials, all the magnetic moment vectors are aligned and the magnet without determining any value of magnetization. In net magnetic moment l of the magnet is equal to NlFe, an advanced lab setting, students can explore numerical val- where N is the number of iron atoms in the magnet. The ues of magnetization of the four types of permanent magnets, magnetization M of the magnet, with a volume V is defined viz., neodymium iron boron (NdFeB), samarium cobalt as5,9 (SmCo), alnico, and ceramic or ferrite magnets. II. THEORY A. Magnetic moment It is well known that in a wire loop with area A, in which a current i is flowing, we define a vector known as the Fig. 1. (a) Magnetic moment of a current carrying loop at an angle h with “magnetic moment” (symbol ~l), perpendicular to the plane respect to B~ and (b) ~l k B~. 275 Am. J. Phys. 87 (4), April 2019 http://aapt.org/ajp VC 2019 American Association of Physics Teachers 275 Fig. 2. Cylindrical permanent magnet of radius R and height l. l M ¼ : (3) Fig. 3. Helmholtz coils of diameter D, consisting of N turns. Image copyright: V https://www.emworks.com/application/numerical-simulation-of-helmholtz-coil. For the cylindrical magnet of Fig. 2, the volume is given by the following equation: V ¼ pR2l: (4) C. Magnetic field at the center of a pair of Helmholtz coils The schematic of a pair of Helmholtz coils is shown in Fig. 3. Each has a diameter D and consists of N turns of wire. They are positioned so that they have a common axis, and the distance between the coil centers is adjusted so that it is equal to half the diameter D. Under these conditions, the Helmholtz coils generate a magnetic field along the common Fig. 4. Cylindrical permanent magnet suspended from strings. axis of the coils, which is uniform in the vicinity of the mid- point between the coil centers. The magnetic field B is given by the following equation:10,11 16l Ni B ¼ pffiffiffiffiffiffiffiffi0 : (5) D 125 Here, the current i is measured in Amps, B is measured in tesla, D ¼ 0:21 m, N ¼ 119, and l0 is a constant equal to 1:256 Â 10À6 T:m=A. III. DISCUSSION: OSCILLATION OF A MAGNET IN A MAGNETIC FIELD A permanent magnet is suspended, in a stirrup like Fig. 5. Top view of the cylindrical magnet oscillating between the arrangement (Fig. 4), so that the magnet points in the Helmholtz coils. Fig. 6. Pictorial representation of the experimental set-up. (a) Schematic and (b) actual working rendition. 276 Am. J. Phys., Vol. 87, No. 4, April 2019 B. Barman and A. Petrou 276 north-south direction. The magnetic field B~ generated by the Table I. Summary of the experimental parameters as well as the calculated Helmholtz coils is in the same direction such that the Earth’s value of M. magnetic field does not influence our measurement of mag- 2 2 À1 netization. This is an important criterion which has to be m (kg) R (m) l (m) l (kg m ) lðAm Þ MðAm Þ kept in consideration while performing this experiment. If 0.0511 0.0046 0.125 6:681 Â 10À5 3.047 ð3761:2Þ104 we now consider Fig. 5, which is a top view of Fig. 4, dis- place the magnet by a small angle /0 from the direction of ~ B, and release it from rest, the magnet will oscillate around between the centers of the coils. Hence, the choice of length the equilibrium position as indicated by the curved arrows for the permanent magnet is paramount to determining M shown in Fig. 5. The time it takes for the magnet to swing precisely. More significantly, the distance between the coils from left to right and back to the starting position is called should be equal to the radius in order to achieve this unifor- the period of oscillation (symbol T). By applying Newton’s mity.13,14 The period of 10 oscillations was measured as a second law of rotational motion, we can write (using the function of the current in the Helmholtz coils; the resulting small angle approximation) data were linearized using Eq. (9) and plotted. A least- squares fit was used to plot the data as shown in Fig. 7.In d2/ s ¼ I ¼ C/ þ lB sin / ½C þ lB /; (6) order to improve the accuracy of these measurements, it is dt2 important that the permanent magnet oscillates in a horizon- tal plane, keeping the small-angle approximation in mind. ~ where / is the angle that the magnet axis forms with B at Any vertical mode of oscillation would introduce a consider- any instant of time t. Here, C is the torsional constant that able amount of error in the measurement of the magnetiza- describes the mechanical properties of the supporting strings tion. Vernier calipers were used to measure the radius R and and l is the magnetic moment of the magnet. I is the moment the length ‘ of the magnet, while a balance was used to mea- of inertia (in our configuration) of the cylindrical magnet of sure the mass m of the magnet in kilograms. mass m and is given by the following equation:12 1 1 V. EXPERIMENTAL RESULTS AND DISCUSSION I ¼ ml2 þ mR2: (7) 12 4 The experimental data were plotted with B on the x-axis andðÞ 2p=T 2 on the y-axis as shown in Fig. 7 followed by The solution to the 2nd order differential equation in / is modeling using Eq. (9) to calculate the magnetic moment l. given by Having determined the slope (and the corresponding mag- netic moment l), together with volume V, we were able to 2p / ¼ / cos t : (8) determine the magnetization M of the magnet.
Load more

Recommended publications
  • Basic Magnetic Measurement Methods
    Basic magnetic measurement methods Magnetic measurements in nanoelectronics 1. Vibrating sample magnetometry and related methods 2. Magnetooptical methods 3. Other methods Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The unit of the magnetic flux density, Tesla (1 T=1 Wb/m2), as a derive unit of Si must be based on some measurement (force, magnetic resonance) *the alternative name is magnetic induction Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The Physikalisch-Technische Bundesanstalt (German national metrology institute) maintains a unit Tesla in form of coils with coil constant k (ratio of the magnetic flux density to the coil current) determined based on NMR measurements graphics from: http://www.ptb.de/cms/fileadmin/internet/fachabteilungen/abteilung_2/2.5_halbleiterphysik_und_magnetismus/2.51/realization.pdf *the alternative name is magnetic induction Introduction It
    [Show full text]
  • Electrostatics Vs Magnetostatics Electrostatics Magnetostatics
    Electrostatics vs Magnetostatics Electrostatics Magnetostatics Stationary charges ⇒ Constant Electric Field Steady currents ⇒ Constant Magnetic Field Coulomb’s Law Biot-Savart’s Law 1 ̂ ̂ 4 4 (Inverse Square Law) (Inverse Square Law) Electric field is the negative gradient of the Magnetic field is the curl of magnetic vector electric scalar potential. potential. 1 ′ ′ ′ ′ 4 |′| 4 |′| Electric Scalar Potential Magnetic Vector Potential Three Poisson’s equations for solving Poisson’s equation for solving electric scalar magnetic vector potential potential. Discrete 2 Physical Dipole ′′′ Continuous Magnetic Dipole Moment Electric Dipole Moment 1 1 1 3 ∙̂̂ 3 ∙̂̂ 4 4 Electric field cause by an electric dipole Magnetic field cause by a magnetic dipole Torque on an electric dipole Torque on a magnetic dipole ∙ ∙ Electric force on an electric dipole Magnetic force on a magnetic dipole ∙ ∙ Electric Potential Energy Magnetic Potential Energy of an electric dipole of a magnetic dipole Electric Dipole Moment per unit volume Magnetic Dipole Moment per unit volume (Polarisation) (Magnetisation) ∙ Volume Bound Charge Density Volume Bound Current Density ∙ Surface Bound Charge Density Surface Bound Current Density Volume Charge Density Volume Current Density Net , Free , Bound Net , Free , Bound Volume Charge Volume Current Net , Free , Bound Net ,Free , Bound 1 = Electric field = Magnetic field = Electric Displacement = Auxiliary
    [Show full text]
  • Permanent Magnet DC Motors Catalog
    Catalog DC05EN Permanent Magnet DC Motors Drives DirectPower Series DA-Series DirectPower Plus Series SC-Series PRO Series www.electrocraft.com www.electrocraft.com For over 60 years, ElectroCraft has been helping engineers translate innovative ideas into reality – one reliable motor at a time. As a global specialist in custom motor and motion technology, we provide the engineering capabilities and worldwide resources you need to succeed. This guide has been developed as a quick reference tool for ElectroCraft products. It is not intended to replace technical documentation or proper use of standards and codes in installation of product. Because of the variety of uses for the products described in this publication, those responsible for the application and use of this product must satisfy themselves that all necessary steps have been taken to ensure that each application and use meets all performance and safety requirements, including all applicable laws, regulations, codes and standards. Reproduction of the contents of this copyrighted publication, in whole or in part without written permission of ElectroCraft is prohibited. Designed by stilbruch · www.stilbruch.me ElectroCraft DirectPower™, DirectPower™ Plus, DA-Series, SC-Series & PRO Series Drives 2 Table of Contents Typical Applications . 3 Which PMDC Motor . 5 PMDC Drive Product Matrix . .6 DirectPower Series . 7 DP20 . 7 DP25 . 9 DP DP30 . 11 DirectPower Plus Series . 13 DPP240 . 13 DPP640 . 15 DPP DPP680 . 17 DPP700 . 19 DPP720 . 21 DA-Series. 23 DA43 . 23 DA DA47 . 25 SC-Series . .27 SCA-L . .27 SCA-S . .29 SC SCA-SS . 31 PRO Series . 33 PRO-A04V36 . 35 PRO-A08V48 . 37 PRO PRO-A10V80 .
    [Show full text]
  • Equivalence of Current–Carrying Coils and Magnets; Magnetic Dipoles; - Law of Attraction and Repulsion, Definition of the Ampere
    GEOPHYSICS (08/430/0012) THE EARTH'S MAGNETIC FIELD OUTLINE Magnetism Magnetic forces: - equivalence of current–carrying coils and magnets; magnetic dipoles; - law of attraction and repulsion, definition of the ampere. Magnetic fields: - magnetic fields from electrical currents and magnets; magnetic induction B and lines of magnetic induction. The geomagnetic field The magnetic elements: (N, E, V) vector components; declination (azimuth) and inclination (dip). The external field: diurnal variations, ionospheric currents, magnetic storms, sunspot activity. The internal field: the dipole and non–dipole fields, secular variations, the geocentric axial dipole hypothesis, geomagnetic reversals, seabed magnetic anomalies, The dynamo model Reasons against an origin in the crust or mantle and reasons suggesting an origin in the fluid outer core. Magnetohydrodynamic dynamo models: motion and eddy currents in the fluid core, mechanical analogues. Background reading: Fowler §3.1 & 7.9.2, Lowrie §5.2 & 5.4 GEOPHYSICS (08/430/0012) MAGNETIC FORCES Magnetic forces are forces associated with the motion of electric charges, either as electric currents in conductors or, in the case of magnetic materials, as the orbital and spin motions of electrons in atoms. Although the concept of a magnetic pole is sometimes useful, it is diácult to relate precisely to observation; for example, all attempts to find a magnetic monopole have failed, and the model of permanent magnets as magnetic dipoles with north and south poles is not particularly accurate. Consequently moving charges are normally regarded as fundamental in magnetism. Basic observations 1. Permanent magnets A magnet attracts iron and steel, the attraction being most marked close to its ends.
    [Show full text]
  • Permanent Magnet Design Guidelines
    NOTE(2019): THIS ORGANIZATION (MMPA) IS OBSOLETE! MAGNET GUIDELINES Basic physics of magnet materials II. Design relationships, figures merit and optimizing techniques Ill. Measuring IV. Magnetizing Stabilizing and handling VI. Specifications, standards and communications VII. Bibliography INTRODUCTION This guide is a supplement to our MMPA Standard No. 0100. It relates the information in the Standard to permanent magnet circuit problems. The guide is a bridge between unit property data and a permanent magnet component having a specific size and geometry in order to establish a magnetic field in a given magnetic circuit environment. The MMPA 0100 defines magnetic, thermal, physical and mechanical properties. The properties given are descriptive in nature and not intended as a basis of acceptance or rejection. Magnetic measure- ments are difficult to make and less accurate than corresponding electrical mea- surements. A considerable amount of detailed information must be exchanged between producer and user if magnetic quantities are to be compared at two locations. MMPA member companies feel that this publication will be helpful in allowing both user and producer to arrive at a realistic and meaningful specifica- tion framework. Acknowledgment The Magnetic Materials Producers Association acknowledges the out- standing contribution of Parker to this and designers and manufacturers of products usingpermanent magnet materials. Parker the Technical Consultant to MMPA compiled and wrote this document. We also wish to thank the Standards and Engineering Com- mittee of MMPA which reviewed and edited this document. December 1987 3M July 1988 5M August 1996 December 1998 1 M CONTENTS The guide is divided into the following sections: Glossary of terms and conversion A very important starting point since the whole basis of communication in the magnetic material industry involves measurement of defined unit properties.
    [Show full text]
  • Module 3 : MAGNETIC FIELD Lecture 20 : Magnetism in Matter
    Module 3 : MAGNETIC FIELD Lecture 20 : Magnetism in Matter Objectives In this lecture you will learn the following Study magnetic properties of matter. Express Ampere's law in the presence of magnetic matter. Define magnetization and H-vector. Understand displacement current. Assemble all the Maxwell's equations together. Study properties and propagation of electromagnetic waves in vacuum. Magnetism in Matter In our discussion on electrostatics, we have seen that in the presence of an electric field, a dielectric gets polarized, leading to bound charges. The polarization vector is, in general, in the direction of the applied electric field. A similar phenomenon occurs when a material medium is subjected to an external magnetic field. However, unlike the behaviour of dielectrics in electric field, different types of material behave in different ways when an external magnetic field is applied. We have seen that the source of magnetic field is electric current. The circulating electrons in an atom, being tiny current loops, constitute a magnetic dipole with a magnetic moment whose direction depends on the direction in which the electron is moving. An atom as a whole, may or may not have a net magnetic moment depending on the way the moments due to different elecronic orbits add up. (The situation gets further complicated because of electron spin, which is a purely quantum concept, that provides an intrinsic magnetic moment to an electron.) In the absence of a magnetic field, the atomic moments in a material are randomly oriented and consequently the net magnetic moment of the material is zero. However, in the presence of a magnetic field, the substance may acquire a net magnetic moment either in the direction of the applied field or in a direction opposite to it.
    [Show full text]
  • Magnetism in Transition Metal Complexes
    Magnetism for Chemists I. Introduction to Magnetism II. Survey of Magnetic Behavior III. Van Vleck’s Equation III. Applications A. Complexed ions and SOC B. Inter-Atomic Magnetic “Exchange” Interactions © 2012, K.S. Suslick Magnetism Intro 1. Magnetic properties depend on # of unpaired e- and how they interact with one another. 2. Magnetic susceptibility measures ease of alignment of electron spins in an external magnetic field . 3. Magnetic response of e- to an external magnetic field ~ 1000 times that of even the most magnetic nuclei. 4. Best definition of a magnet: a solid in which more electrons point in one direction than in any other direction © 2012, K.S. Suslick 1 Uses of Magnetic Susceptibility 1. Determine # of unpaired e- 2. Magnitude of Spin-Orbit Coupling. 3. Thermal populations of low lying excited states (e.g., spin-crossover complexes). 4. Intra- and Inter- Molecular magnetic exchange interactions. © 2012, K.S. Suslick Response to a Magnetic Field • For a given Hexternal, the magnetic field in the material is B B = Magnetic Induction (tesla) inside the material current I • Magnetic susceptibility, (dimensionless) B > 0 measures the vacuum = 0 material response < 0 relative to a vacuum. H © 2012, K.S. Suslick 2 Magnetic field definitions B – magnetic induction Two quantities H – magnetic intensity describing a magnetic field (Système Internationale, SI) In vacuum: B = µ0H -7 -2 µ0 = 4π · 10 N A - the permeability of free space (the permeability constant) B = H (cgs: centimeter, gram, second) © 2012, K.S. Suslick Magnetism: Definitions The magnetic field inside a substance differs from the free- space value of the applied field: → → → H = H0 + ∆H inside sample applied field shielding/deshielding due to induced internal field Usually, this equation is rewritten as (physicists use B for H): → → → B = H0 + 4 π M magnetic induction magnetization (mag.
    [Show full text]
  • An Inexpensive Hands-On Introduction to Permanent Magnet Direct Current Motors
    AC 2011-1082: AN INEXPENSIVE HANDS-ON INTRODUCTION TO PER- MANENT MAGNET DIRECT CURRENT MOTORS Garrett M. Clayton, Villanova University Dr. Garrett M. Clayton received his BSME from Seattle University and his MSME and PhD in Mechanical Engineering from the University of Washington (Seattle). He is an Assistant Professor in Mechanical Engineering at Villanova University. His research interests focus on mechatronics, specifically modeling and control of scanning probe microscopes and unmanned vehicles. Rebecca A Stein, University of Pennsylvania Rebecca Stein is the Associate Director of Research and Educational Outreach in the School of Engi- neering and Applied Science at the University of Pennsylvania. She received her B.S. in Mechanical Engineering and Masters in Technology Management from Villanova University. Her background and work experience is in K-12 engineering education initiatives. Rebecca has spent the past 5 years involved in STEM high school programs at Villanova University and The School District of Philadelphia. Ad- ditionally, she has helped coordinate numerous robotics competitions such as BEST Robotics, FIRST LEGO League and MATE. Page 22.177.1 Page c American Society for Engineering Education, 2011 An Inexpensive Hands-on Introduction to Permanent Magnet Direct Current Motors Abstract Motors are an important curricular component in freshman and sophomore introduction to mechanical engineering (ME) courses as well as in curricula developed for high school science and robotics clubs. In order to facilitate a hands-on introduction to motors, an inexpensive permanent magnet direct current (PMDC) motor experiment has been developed that gives students an opportunity to build a PMDC motor from common office supplies along with a few inexpensive laboratory components.
    [Show full text]
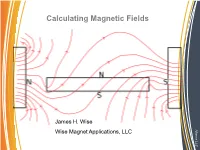
  • Calculating Magnetic Fields, Please Call
    Calculating Magnetic Fields James H. Wise Alliance LLC Alliance Wise Magnet Applications, LLC Magnetic Fields: What and Where? Magnetic fields: Sources: • Appear around electric currents • Surround magnetic materials Properties: • They have a direction • They possess magnitude • They are vector fields Alliance LLC Alliance Reference for Definition Field descriptions and behavior See Chapters 1, 2 and 3 of “The Feynman Lectures in Physics”, Vol.II by Feynman, Leighton and Sands, Addison Wesley,1964, ISBN 0 -201-2117-X-P . Chapter 1 is my favorite starting point for thinking about fields. The next slide is derived from that. Alliance LLC Alliance Examples of Fields Fields: • When a quantity varies with location in space, (x,y,z,t), it is said to be a field. • Temperature around a heat source forms a field. • As the temperature is only a single quantity associated with it is said to be a scalar field • Heat flow has a direction and thus 3 quantities that change with (x,y,z) and perhaps a time dependence • Because it has 3 spatial components obeying the rules of vectors, it is said to be a vector field. Alliance LLC Alliance Magnetic Fields of Permanent Magnets • The magnetic field was originally treated as originating from charges. • Pole strength was interpreted as the amount of magnetic charge on the surface of a magnet If the charge distribution was known, the force outside the magnet could be computed correctly • The charge model does not give the correct results for fields inside magnets. • The pole model is useful for gaining an intuitive view for qualitative results.
    [Show full text]
  • Electromagnetism 3. Magnetization (Lectures 7–9)
    Electromagnetism Handout 3: 3. Magnetization (Lectures 7{9): Here is the proof of a useful vector identity. First recall Stokes' theorem which states that Z I r × A · dS = A · dl: (1) Let us suppose that A takes the form A(r) = f(r)c where c 6= c(r) is a constant vector. Hence we have r × A = fr × c − c × rf = −c × rf (2) since r × c = 0 (because c is a constant vector, its derivative vanishes). Stokes' theorem then gives us I I Z Z A · dl = c · f dl = − c × rf · dS = −c · rf × dS; (3) but this is true for any c and so I Z f dl = − rf × dS: (4) Now let us choose f = r^ · r0 and take the gradient and integral around a closed loop in the primed coordinates: I Z Z (r^ · r0) dl0 = − r0(r^ · r0) × dS0 = −r^ × dS0 (5) which works because r0(r^ · r0) = r^. In summary: I Z r^ · r0 dl0 = dS0 × r^: (6) We will use this to show that the magnetic vector potential from a magnetic dipole is given by µ A = 0 m × r^; (7) 4πr2 where m is the magnetic dipole moment. For example, if we put m parallel to z and use spherical polars, we have that µ A = 0 m sin θ φ^; (8) 4πr2 and so 1 @ 1 @ B = r × A(r) = (r sin θ A )r^ − (r sin θ A )θ^; (9) r2 sin θ @θ φ r sin θ @r φ because Ar = Aθ = 0 and hence µ m 2 cos θ sin θ B = 0 r^ + θ^ ; (10) 4π r3 r3 which is the same form as an electric dipole.
    [Show full text]
  • Exploring the Earth's Magnetic Field
    ([SORULQJWKH(DUWK·V0DJQHWLF)LHOG $Q,0$*(6DWHOOLWH*XLGHWRWKH0DJQHWRVSKHUH An IMAGE Satellite Guide to Exploring the Earth’s Magnetic Field 1 $FNQRZOHGJPHQWV Dr. James Burch IMAGE Principal Investigator Dr. William Taylor IMAGE Education and Public Outreach Raytheon ITS and NASA Goddard SFC Dr. Sten Odenwald IMAGE Education and Public Outreach Raytheon ITS and NASA Goddard SFC Ms. Annie DiMarco This resource was developed by Greenwood Elementary School the NASA Imager for Brookville, Maryland Magnetopause-to-Auroral Global Exploration (IMAGE) Ms. Susan Higley Cherry Hill Middle School Information about the IMAGE Elkton, Maryland Mission is available at: http://image.gsfc.nasa.gov Mr. Bill Pine http://pluto.space.swri.edu/IMAGE Chaffey High School Resources for teachers and Ontario, California students are available at: Mr. Tom Smith http://image.gsfc.nasa.gov/poetry Briggs-Chaney Middle School Silver Spring, Maryland Cover Artwork: Image of the Earth’s ring current observed by the IMAGE, HENA instrument. Some representative magnetic field lines are shown in white. An IMAGE Satellite Guide to Exploring the Earth’s Magnetic Field 2 &RQWHQWV Chapter 1: What is a Magnet? , *UDGH 3OD\LQJ:LWK0DJQHWLVP ,, *UDGH ([SORULQJ0DJQHWLF)LHOGV ,,, *UDGH ([SORULQJWKH(DUWKDVD0DJQHW ,9 *UDGH (OHFWULFLW\DQG0DJQHWLVP Chapter 2: Investigating Earth’s Magnetism 9 *UDGH *UDGH7KH:DQGHULQJ0DJQHWLF3ROH 9, *UDGH 3ORWWLQJ3RLQWVLQ3RODU&RRUGLQDWHV 9,, *UDGH 0HDVXULQJ'LVWDQFHVRQWKH3RODU0DS 9,,, *UDGH :DQGHULQJ3ROHVLQWKH/DVW<HDUV ,; *UDGH 7KH0DJQHWRVSKHUHDQG8V
    [Show full text]
  • Vocabulary of Magnetism
    TECHNotes The Vocabulary of Magnetism Symbols for key magnetic parameters continue to maximum energy point and the value of B•H at represent a challenge: they are changing and vary this point is the maximum energy product. (You by author, country and company. Here are a few may have noticed that typing the parentheses equivalent symbols for selected parameters. for (BH)MAX conveniently avoids autocorrecting Subscripts in symbols are often ignored so as to the two sequential capital letters). Units of simplify writing and typing. The subscripted letters maximum energy product are kilojoules per are sometimes capital letters to be more legible. In cubic meter, kJ/m3 (SI) and megagauss•oersted, ASTM documents, symbols are italicized. According MGOe (cgs). to NIST’s guide for the use of SI, symbols are not italicized. IEC uses italics for the main part of the • µr = µrec = µ(rec) = recoil permeability is symbol, but not for the subscripts. I have not used measured on the normal curve. It has also been italics in the following definitions. For additional called relative recoil permeability. When information the reader is directed to ASTM A340[11] referring to the corresponding slope on the and the NIST Guide to the use of SI[12]. Be sure to intrinsic curve it is called the intrinsic recoil read the latest edition of ASTM A340 as it is permeability. In the cgs-Gaussian system where undergoing continual updating to be made 1 gauss equals 1 oersted, the intrinsic recoil consistent with industry, NIST and IEC usage. equals the normal recoil minus 1.
    [Show full text]