An Induction Principle Over Real Numbers Assia Mahboubi
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Elementary Number Theory and Methods of Proof
CHAPTER 4 ELEMENTARY NUMBER THEORY AND METHODS OF PROOF Copyright © Cengage Learning. All rights reserved. SECTION 4.4 Direct Proof and Counterexample IV: Division into Cases and the Quotient-Remainder Theorem Copyright © Cengage Learning. All rights reserved. Direct Proof and Counterexample IV: Division into Cases and the Quotient-Remainder Theorem The quotient-remainder theorem says that when any integer n is divided by any positive integer d, the result is a quotient q and a nonnegative remainder r that is smaller than d. 3 Example 1 – The Quotient-Remainder Theorem For each of the following values of n and d, find integers q and r such that and a. n = 54, d = 4 b. n = –54, d = 4 c. n = 54, d = 70 Solution: a. b. c. 4 div and mod 5 div and mod A number of computer languages have built-in functions that enable you to compute many values of q and r for the quotient-remainder theorem. These functions are called div and mod in Pascal, are called / and % in C and C++, are called / and % in Java, and are called / (or \) and mod in .NET. The functions give the values that satisfy the quotient-remainder theorem when a nonnegative integer n is divided by a positive integer d and the result is assigned to an integer variable. 6 div and mod However, they do not give the values that satisfy the quotient-remainder theorem when a negative integer n is divided by a positive integer d. 7 div and mod For instance, to compute n div d for a nonnegative integer n and a positive integer d, you just divide n by d and ignore the part of the answer to the right of the decimal point. -

Introduction to Uncertainties (Prepared for Physics 15 and 17)
Introduction to Uncertainties (prepared for physics 15 and 17) Average deviation. When you have repeated the same measurement several times, common sense suggests that your “best” result is the average value of the numbers. We still need to know how “good” this average value is. One measure is called the average deviation. The average deviation or “RMS deviation” of a data set is the average value of the absolute value of the differences between the individual data numbers and the average of the data set. For example if the average is 23.5cm/s, and the average deviation is 0.7cm/s, then the number can be expressed as (23.5 ± 0.7) cm/sec. Rule 0. Numerical and fractional uncertainties. The uncertainty in a quantity can be expressed in numerical or fractional forms. Thus in the above example, ± 0.7 cm/sec is a numerical uncertainty, but we could also express it as ± 2.98% , which is a fraction or %. (Remember, %’s are hundredths.) Rule 1. Addition and subtraction. If you are adding or subtracting two uncertain numbers, then the numerical uncertainty of the sum or difference is the sum of the numerical uncertainties of the two numbers. For example, if A = 3.4± .5 m and B = 6.3± .2 m, then A+B = 9.7± .7 m , and A- B = - 2.9± .7 m. Notice that the numerical uncertainty is the same in these two cases, but the fractional uncertainty is very different. Rule2. Multiplication and division. If you are multiplying or dividing two uncertain numbers, then the fractional uncertainty of the product or quotient is the sum of the fractional uncertainties of the two numbers. -

Unit 6: Multiply & Divide Fractions Key Words to Know
Unit 6: Multiply & Divide Fractions Learning Targets: LT 1: Interpret a fraction as division of the numerator by the denominator (a/b = a ÷ b) LT 2: Solve word problems involving division of whole numbers leading to answers in the form of fractions or mixed numbers, e.g. by using visual fraction models or equations to represent the problem. LT 3: Apply and extend previous understanding of multiplication to multiply a fraction or whole number by a fraction. LT 4: Interpret the product (a/b) q ÷ b. LT 5: Use a visual fraction model. Conversation Starters: Key Words § How are fractions like division problems? (for to Know example: If 9 people want to shar a 50-lb *Fraction sack of rice equally by *Numerator weight, how many pounds *Denominator of rice should each *Mixed number *Improper fraction person get?) *Product § 3 pizzas at 10 slices each *Equation need to be divided by 14 *Division friends. How many pieces would each friend receive? § How can a model help us make sense of a problem? Fractions as Division Students will interpret a fraction as division of the numerator by the { denominator. } What does a fraction as division look like? How can I support this Important Steps strategy at home? - Frac&ons are another way to Practice show division. https://www.khanacademy.org/math/cc- - Fractions are equal size pieces of a fifth-grade-math/cc-5th-fractions-topic/ whole. tcc-5th-fractions-as-division/v/fractions- - The numerator becomes the as-division dividend and the denominator becomes the divisor. Quotient as a Fraction Students will solve real world problems by dividing whole numbers that have a quotient resulting in a fraction. -

Division Into Cases and the Quotient-Remainder Theorem
4.4 Direct Proof and Counterexample IV: Division into Cases and the Quotient-Remainder Theorem 4.4 Quotient-Remainder Theorem 1 / 4 1 n = 34 and d = 6. 2 n = −34 and d = 6. Examples For each of the following values of n and d, find integers q and r such that n = dq + r and 0 ≤ r < d. The Quotient-Remainder Theorem Theorem Given any integer n and positive integer d, there exist unique integers q and r such that n = dq + r and 0 ≤ r < d: 4.4 Quotient-Remainder Theorem 2 / 4 2 n = −34 and d = 6. The Quotient-Remainder Theorem Theorem Given any integer n and positive integer d, there exist unique integers q and r such that n = dq + r and 0 ≤ r < d: Examples For each of the following values of n and d, find integers q and r such that n = dq + r and 0 ≤ r < d. 1 n = 34 and d = 6. 4.4 Quotient-Remainder Theorem 2 / 4 The Quotient-Remainder Theorem Theorem Given any integer n and positive integer d, there exist unique integers q and r such that n = dq + r and 0 ≤ r < d: Examples For each of the following values of n and d, find integers q and r such that n = dq + r and 0 ≤ r < d. 1 n = 34 and d = 6. 2 n = −34 and d = 6. 4.4 Quotient-Remainder Theorem 2 / 4 1 Compute 33 div 9 and 33 mod 9 (by hand and Python). 2 Keeping in mind which years are leap years, what day of the week will be 1 year from today? 3 Suppose that m is an integer. -

Eureka Math™ Tips for Parents Module 2
Grade 6 Eureka Math™ Tips for Parents Module 2 The chart below shows the relationships between various fractions and may be a great Key Words tool for your child throughout this module. Greatest Common Factor In this 19-lesson module, students complete The greatest common factor of two whole numbers (not both zero) is the their understanding of the four operations as they study division of whole numbers, division greatest whole number that is a by a fraction, division of decimals and factor of each number. For operations on multi-digit decimals. This example, the GCF of 24 and 36 is 12 expanded understanding serves to complete because when all of the factors of their study of the four operations with positive 24 and 36 are listed, the largest rational numbers, preparing students for factor they share is 12. understanding, locating, and ordering negative rational numbers and working with algebraic Least Common Multiple expressions. The least common multiple of two whole numbers is the least whole number greater than zero that is a What Came Before this Module: multiple of each number. For Below is an example of how a fraction bar model can be used to represent the Students added, subtracted, and example, the LCM of 4 and 6 is 12 quotient in a division problem. multiplied fractions and decimals (to because when the multiples of 4 and the hundredths place). They divided a 6 are listed, the smallest or first unit fraction by a non-zero whole multiple they share is 12. number as well as divided a whole number by a unit fraction. -

Facultad De Matemáticas, Univ. De Sevilla, Sevilla, Spain Arias@ Us. Es
#A51 INTEGERS 18 (2018) ARITHMETIC OF THE FABIUS FUNCTION J. Arias de Reyna1 Facultad de Matem´aticas, Univ. de Sevilla, Sevilla, Spain [email protected] Received: 5/29/17, Revised: 2/27/18, Accepted: 5/31/18, Published: 6/5/18 Abstract The Fabius function was defined in 1935 by Jessen and Wintner and has been independently defined at least six times since. We attempt to unify notations re- lated to the Fabius function. The Fabius function F (x) takes rational values at dyadic points. We study the arithmetic of these rational numbers. In partic- ular, we define two sequences of natural numbers that determine these rational numbers. Using these sequences we solve a conjecture raised in MathOverflow by n Vladimir Reshetnikov. We determine the dyadic valuation of F (2− ), showing that n n ⌫2(F (2− )) = 2 ⌫2(n!) 1. We give the proof of a formula that allows an efficient computation− −of exact−or approximate values of F (x). 1. Introduction The Fabius function is a natural object. It is not surprising that it has been inde- pendently defined several times. As far as we know it was defined independently in the following cases: 1. In 1935 by B. Jessen and A. Wintner [7, Ex. 5, p. 62] (English). They showed in five lines that it is infinitely di↵erentiable. 2. In 1966 by J. Fabius [4] (English); considered as the distribution function of a random variable. 3. In 1971 by V. A. Rvach¨ev [12] (Ukrainian); defined as a solution to the equa- tion y0(x) = 2(y(2x + 1) y(2x 1)). -

Math 1312 Section 5.1 Ratios, Rates, and Proportions Definition
Math 1312 Section 5.1 Ratios, Rates, and Proportions Definition : a A ratio is the quotient , where b ≠ 0 that provides comparison between the numbers a b and b . Units of measure found in a ratio must be convertible to the same unit of measure. Example 1 : The ratio of two numbers (a and b) may be written in a variety of ways. a a ÷ b a to b a : b b In writing the ratio of two numbers, it is usually helpful to express the ratio (fraction) in simplest form. 50 1 Example 2: = 100 2 Example 3: Find the best form of each ratio: 8 a) 4 8 b) 12 4m c) 60 cm Definition : A rate is a quotient, that compares two quantities that cannot be converted to the same unit of measure. 60 miles 12 teaspoons Example 4: 3gallons 2quarts Definition : An equation that states that two ratios are equal is called a proportion . a c = b d The first and last terms ( a and d ) of the proportion are the extremes . The second and third terms are the means . Property 1: (Means - Extremes Property) In a proportion, the product of the means equals the product of the extremes. a c If = , b ≠ 0 and d ≠ 0 , then a × d = b × c b d Example 5: Use the means-extremes property to solve each proportion for x. x 5 a) = 8 12 x 5 b) = 20 x x + 2 4 c) = 5 x +1 Property 2: In a proportion, the means or the extremes (or both) may be interchanged. -

Division of Whole Numbers
The Improving Mathematics Education in Schools (TIMES) Project NUMBER AND ALGEBRA Module 10 DIVISION OF WHOLE NUMBERS A guide for teachers - Years 4–7 June 2011 4YEARS 7 Polynomials (Number and Algebra: Module 10) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑ NonCommercial‑NoDerivs 3.0 Unported License. 2011. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project NUMBER AND ALGEBRA Module 10 DIVISION OF WHOLE NUMBERS A guide for teachers - Years 4–7 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge 4YEARS 7 {4} A guide for teachers DIVISION OF WHOLE NUMBERS ASSUMED KNOWLEDGE • An understanding of the Hindu‑Arabic notation and place value as applied to whole numbers (see the module Using place value to write numbers). • An understanding of, and fluency with, forwards and backwards skip‑counting. • An understanding of, and fluency with, addition, subtraction and multiplication, including the use of algorithms. -

MATH TODAY Grade 5, Module 4, Topic G
MATH TODAY Grade 5, Module 4, Topic G 5th Grade Math Focus Area– Topic G Module 4: Multiplication and Division of Fractions and Decimal Fractions Module 4: Multiplication and Division of Fractions and Decimal Fractions Divide a whole number by a unit fraction Math Parent Letter Garret is running a 5-K race. There are water stops every This document is created to give parents and students a better kilometer, including at the finish line. How many water stops will understanding of the math concepts found in the Engage New there be? Number Sentence: 5 ÷ York material which is taught in the classroom. Module 4 of Step 1: Draw a tape diagram to model the problem. Engage New York covers multiplication and division of fractions 5 and decimal fractions. This newsletter will discuss Module 4, Topic G. In this topic students will explore the meaning of division with fractions and decimal fractions. The tape diagram is partitioned into 5 equal units. Each unit Topic G: Division of Fractions and Decimal Fractions represents 1 kilometer of the race. Words to know: Step 2: Since water stops are every kilometer, each unit of the divide/division quotient tape diagram is divided into 2 equal parts. divisor dividend 5 unit fraction decimal fraction decimal divisor tenths hundredths Things to Remember! 1st Last Quotient – the answer of dividing one quantity by another stop stop Unit Fraction – a fraction with a numerator of 1 When you count the number of halves in the tape diagram, you Decimal Fraction – a fraction whose denominator is a power of will determine that there are a total of 10. -

The Minkowski Question Mark Function: Explicit Series for the Dyadic Period Function and Moments
MATHEMATICS OF COMPUTATION Volume 79, Number 269, January 2010, Pages 383–418 S 0025-5718(09)02263-7 Article electronically published on May 12, 2009 THE MINKOWSKI QUESTION MARK FUNCTION: EXPLICIT SERIES FOR THE DYADIC PERIOD FUNCTION AND MOMENTS GIEDRIUS ALKAUSKAS Abstract. Previously, several natural integral transforms of the Minkowski question mark function F (x) were introduced by the author. Each of them is uniquely characterized by certain regularity conditions and the functional equation, thus encoding intrinsic information about F (x). One of them, the dyadic period function G(z), was defined as a Stieltjes transform. In this paper we introduce a family of “distributions” Fp(x)forp ≥ 1, such that F1(x)is the question mark function and F2(x) is a discrete distribution with support on x = 1. We prove that the generating function of moments of Fp(x)satisfies the three-term functional equation. This has an independent interest, though our main concern is the information it provides about F (x). This approach yields the following main result: we prove that the dyadic period function is a sum of infinite series of rational functions with rational coefficients. 1. Introduction and main result The aim of this paper is to continue investigations on the moments of the Minkowski ?(x) function, begun in [1], [2] and [3]. The function ?(x) (“the question mark function”) was introduced by Minkowski as an example of a continuous func- tion F :[0, ∞) → [0, 1), which maps rationals to dyadic rationals, and quadratic irrationals to nondyadic rationals. For a nonnegative real x it is defined by the expression −a0 −(a0+a1) −(a0+a1+a2) (1) F ([a0,a1,a2,a3, ...]) = 1 − 2 +2 − 2 + ..., where x =[a0,a1,a2,a3, ...] stands for the representation of x by a (regular) con- tinued fraction [15]. -

LC12 High-Bright Monitor
Product Specification - LC12 High-Bright Monitor Document Number: 023-0284-01 Revision: A Title: Product Specification: LC12 High- Bright AMLCD Monitor Page 1 of 24 Document Number: 023-0284-01 Revision: A Table of Contents 1.0 INTRODUCTION.......................................................................................................................................................................................4 1.1 Display Format.................................................................................................................... 4 2.0 BASIC CONSTRUCTION........................................................................................................................................................................5 2.1 Weight................................................................................................................................. 5 2.2 Mechanical Mounting Requirements.................................................................................. 5 2.3 Monitor Electronics............................................................................................................. 5 2.4 Cooling Fan......................................................................................................................... 5 2.5 Vandal Glass ....................................................................................................................... 5 2.6 Air Filtration...................................................................................................................... -
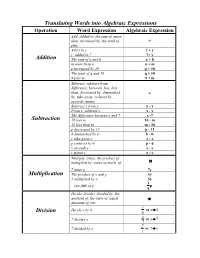
Translating Words Into Algebraic Expressions Addition Subtraction Multiplication Division
Translating Words into Algebraic Expressions Operation Word Expression Algebraic Expression Add, Added to, the sum of, more than, increased by, the total of, + plus Add x to y x + y y added to 7 7+ y Addition The sum of a and b a + b m more than n n + m p increased by 10 p + 10 The total of q and 10 q + 10 9 plus m 9 + m Subtract, subtract from, difference, between, less, less than, decreased by, diminished - by, take away, reduced by, exceeds, minus Subtract x from y y - x From x, subtract y x - y The difference between x and 7 x -7 Subtraction 10 less m 10 - m 10 less than m m - 10 p decreased by 11 p - 11 8 diminished by w 8 - w y take away z y - z p reduced by 6 p - 6 x exceeds y x - y r minus s r - s Multiply, times, the product of, multiplied by, times as much, of × 7 times y 7y Multiplication The product of x and y xy 5 multiplied by y 5y 1 one-fifth of p p 5 Divide, divides, divided by, the quotient of, the ratio of, equal ÷ amounts of, per x Divide x by 6 or x ÷ 6 Division 6 x 7 divides x or x ÷ 7 7 7 7 divided by x or 7 ÷ x x y The quotient of y and 5 or y ÷ 5 5 u The ratio of u to v or u ÷ v v u Division u separated into 4 equal parts or u ÷ 4 (continued) 4 5 5 parts per 100 parts 100 The square of y y2 Power The cube of k k3 t raised to the fourth power t4 Is equal to, the same as, is, are, the result of, will be, are, yields = Equals x is equal to y x = y p is the same as q p = q Two, two times, twice, twice as Multiplication by much as, double 2 2 Twice z 2z y doubled 2y 1 Half of, one-half of, half as much as, one-half