DOCSLIB.ORG

Qt8b18n6c6 Nosplash Caf9e24

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Qt8b18n6c6 Nosplash Caf9e24 Copyright 2014 by Christopher K. Fuller ii For Kai and Lena iii Acknowledgements This work would not have been possible without the support of my research advisor Hao Li. His broad base of interests gave me the freedom to search for something that so well matches my inclinations. I appreciate his insight, enthusiasm, skepticism, and overall encouragement of this effort. I wish to thank my committee, Saunak Sen and Kathleen Giacomini, for their suggestions and support. I wish to thank postdoctoral scholar Xin He for catalyzing the research that became the focus of my work. In addition, I wish to thank postdoctoral scholar Jiashun Zheng for his numerous suggestions and support. I wish to thank the thousands of anonymous individuals who make integrative genomics research possible by providing samples and the researchers dedicated to making these widely available. In addition, I wish to thank the MuTHER and DIAGRAM consortia for providing access to their full summary results. I wish to thank my wife, Sharoni, for her support and for permitting me to encroach on her domain of expertise. You are still the real biologist in the family. Finally, I wish to thank my Mom and Dad ... who took me to the library. iv Abstract Genome-wide association studies (GWAS) have linked various complex diseases to many dozens, sometimes hundreds, of individual genomic loci. Since these are generally of small effect and may lack both functional annotations and an obvious relation to other disease-associated regions, they are difficult to place in a functional context that advances our understanding of the disease. When considered only in isolation, disparate collections of trait associations provide little mechanistic insight. Thus, there is a pressing need for computational methods that use genome-wide molecular data to aggregate GWAS associations and extract functional insight from seemingly unrelated SNPs. To this end, we recently introduced Sherlock, a Bayesian method that detects gene-disease associations through pattern matching between eQTL results and the the full set of GWAS loci (He et al., 2013). Here we review the Bayesian formulation and present Empirical Sherlock, a robust, parameter-free approach to detecting associations between various molecular functions and GWAS traits. It uses an empirically-derived null distribution to associate subsets of GWAS loci, grouped by their relevance to a particular molecular function, with the GWAS trait. The method is easily generalizable to most any genome-wide functional characterization (e.g. DNA methylation, transcription factor binding, etc.), in addition to eQTL. By avoiding null distributions that assume a particular theoretical form for the input GWAS, Empirical Sherlock yields results are resistant to false discovery due to inflation of the output p-values. The core method requires no tunable parameters or prior probabilities and, when used with eQTL, permits an adjustment for pleiotropic SNPs that control the expression of many genes. In addition, Empirical Sherlock calculates significance directly, avoiding the inherent limitations of permutation- based tests. As we demonstrate using moderately-powered GWAS for Crohn's disease, type 2 diabetes, and Schizophrenia, it detects gene associations that are either validated through better-powered GWAS or supported by independent literature. v Contents Contents vi 1 Introduction 1 2 Bayesian Sherlock Method 7 2.1 Model Derivation ...........................................7 2.2 Model Behavior and Parameter Estimation ............................ 10 2.3 Statistical Significance of Gene Bayes Factors ........................... 11 2.4 Summary of Results: Crohn's Disease ............................... 11 2.5 Summary of Results: Type 2 Diabetes ............................... 12 3 Empirical Sherlock Method 14 3.1 Method Overview ........................................... 14 3.2 Identifying Tag SNPs for Independent Blocks ........................... 15 3.3 Core Statistical Method ....................................... 16 3.4 Correcting for Pleiotropic and Sampling Effects .......................... 18 3.5 Avoiding Arbitrary Thresholding of Functional Data ....................... 19 3.6 Performance Verification ...................................... 19 4 Empirical Sherlock Analyses Using Multi-tissue eQTL 23 4.1 Crohn's Disease ............................................ 23 4.2 Type 2 Diabetes ............................................ 26 4.3 Schizophrenia ............................................. 28 5 Discussion 32 A Null Distribution Under Uniform Assumption 36 B Supporting SNPs for Top Crohn's Results 38 C Supporting SNPs for Top T2D Results 73 D Supporting SNPs for Top Schizophrenia Results 83 Bibliography 120 vi Chapter 1 Introduction The genetic underpinnings of complex disease have proven resistant to easy mapping using only the com- mon polymorphisms directly implicated through genome-wide association studies (GWAS). Typically, such studies reveal large numbers of small effect loci that, in aggregate, explain only a small fraction of complex disease heritability. This discrepancy has generated considerable debate concerning the specific mechanisms of polygenic trait inheritance and the overall utility of the GWAS paradigm.1 2 3 By assembling ever-larger disease cohorts, the power to resolve small effects through association studies improves, but this does not necessarily translate into superior mechanistic insight. The functional consequence of a given locus is of- ten non-obvious, especially for the many associations located in intergenic regions. Even when accurate annotations are available, the challenge of assembling many dozens or hundreds of associated loci into a coherent picture of disease etiology is daunting. The ability to reliably map large numbers of associated loci onto a smaller number of functional elements constitutes a key component of a pipeline to convert disparate associations into meaningful disease insight. For these reasons, there is much interest in mining GWAS results using a diverse array of genome- wide indicators of functional relevance. These include assays for chromatin structure, DNA methylation, transcription factor binding activity, and gene expression regulation, as made publicly available through the NHGRI's Encyclopedia of of DNA Elements (ENCODE) project and the NIH-funded Genotype-Tissue Expression (GTEx) program, among others.4 5 Taken together, they form a dictionary of genomic loci in terms of distinct but related molecular phenotypes that can be used to understand the key drivers of complex diseases and other traits. In typical use, however, these molecular definitions provide clues only one-by-one for the top GWAS SNPs (those near or above genome-wide significance). Yet, to be especially useful, improved approaches for GWAS data mining must reflect both the need to gain functional insight and the need to aggregate many SNPs to explain a larger fraction of the inherited 1 phenotypic variance. Although the degree to which missing heritability is captured by rare genetic variants, higher-order genetic interactions (epistasis), or small effects across many common SNPs is the subject of active debate, approaches that mine small effects from SNPs below genome-wide significance are highly attractive, since data is readily available from existing studies.2 6 7 Several lines of evidence suggest that much additional information can be gleaned from common SNPs that fall below genome-wide statistical significance: First, the number of statistically-significant small-effect loci associated with a given trait is limited primarily by the power of the studies involved, not necessarily by some intrinsic property of biological network architecture. An analysis of the current NHGRI GWAS Catalog reveals an exponential distribution of reported effect sizes, with a few large effect loci interspersed with large numbers of small effects.8 Across all studies, the median odds ratio (OR) is well-below 1.3 (Fig. 1.1). With current and planned studies routinely targeting many tens of thousands of individuals in disease cohorts, the number of small effect loci that reach genome-wide significance will only increase. Figure 1.1: Histogram of of odds ratios from all entries in the GWAS catalog through 2012. Large effects are rare, while the number of small effects discovered relates largely to the statistical power of the GWAS studies undertaken. Second, work in model systems indicates that an accumulation of small effects can explain most heritabil- ity for some traits. For example, association studies performed in a panel of yeast segregants may achieve much higher statistical power than typical human GWAS. In a study of 46 traits, the inclusion of small effect loci enabled between 72% and 100% of the narrow-sense (additive) heritability to be explained.9 Although 2 epistasis appeared to contribute to phenotypic variation for many traits, additive effects constituted the dominant component of broad-sense heritability in most cases. For highly additive traits, it was possible to predict trait values using genotypes, but only when very small effect loci were included. Lastly, recent efforts have demonstrated that the phenotypic variance explained by all SNPs in human GWAS, when considered in aggregate, can be significantly higher than that of just the top SNPs and may approach the heritability estimates of twin and pedigree studies.3 For example, the heritability of human height is approximately 0.8, while the phenotypic variance accounted for by 180 top
Load more

Recommended publications
  • Hyaluronidase PH20 (SPAM1) Rabbit Polyclonal Antibody – TA337855
    OriGene Technologies, Inc. 9620 Medical Center Drive, Ste 200 Rockville, MD 20850, US Phone: +1-888-267-4436 [email protected] EU: [email protected] CN: [email protected] Product datasheet for TA337855 Hyaluronidase PH20 (SPAM1) Rabbit Polyclonal Antibody Product data: Product Type: Primary Antibodies Applications: WB Recommended Dilution: WB Reactivity: Human Host: Rabbit Isotype: IgG Clonality: Polyclonal Immunogen: The immunogen for anti-SPAM1 antibody is: synthetic peptide directed towards the C- terminal region of Human SPAM1. Synthetic peptide located within the following region: CYSTLSCKEKADVKDTDAVDVCIADGVCIDAFLKPPMETEEPQIFYNASP Formulation: Liquid. Purified antibody supplied in 1x PBS buffer with 0.09% (w/v) sodium azide and 2% sucrose. Note that this product is shipped as lyophilized powder to China customers. Purification: Affinity Purified Conjugation: Unconjugated Storage: Store at -20°C as received. Stability: Stable for 12 months from date of receipt. Predicted Protein Size: 58 kDa Gene Name: sperm adhesion molecule 1 Database Link: NP_694859 Entrez Gene 6677 Human P38567 This product is to be used for laboratory only. Not for diagnostic or therapeutic use. View online » ©2021 OriGene Technologies, Inc., 9620 Medical Center Drive, Ste 200, Rockville, MD 20850, US 1 / 3 Hyaluronidase PH20 (SPAM1) Rabbit Polyclonal Antibody – TA337855 Background: Hyaluronidase degrades hyaluronic acid, a major structural proteoglycan found in extracellular matrices and basement membranes. Six members of the hyaluronidase family are clustered into two tightly linked groups on chromosome 3p21.3 and 7q31.3. This gene was previously referred to as HYAL1 and HYA1 and has since been assigned the official symbol SPAM1; another family member on chromosome 3p21.3 has been assigned HYAL1.
    [Show full text]
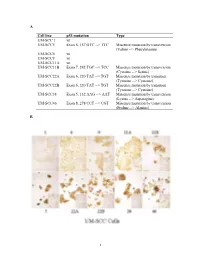
  • A Cell Line P53 Mutation Type UM
    A Cell line p53 mutation Type UM-SCC 1 wt UM-SCC5 Exon 5, 157 GTC --> TTC Missense mutation by transversion (Valine --> Phenylalanine UM-SCC6 wt UM-SCC9 wt UM-SCC11A wt UM-SCC11B Exon 7, 242 TGC --> TCC Missense mutation by transversion (Cysteine --> Serine) UM-SCC22A Exon 6, 220 TAT --> TGT Missense mutation by transition (Tyrosine --> Cysteine) UM-SCC22B Exon 6, 220 TAT --> TGT Missense mutation by transition (Tyrosine --> Cysteine) UM-SCC38 Exon 5, 132 AAG --> AAT Missense mutation by transversion (Lysine --> Asparagine) UM-SCC46 Exon 8, 278 CCT --> CGT Missense mutation by transversion (Proline --> Alanine) B 1 Supplementary Methods Cell Lines and Cell Culture A panel of ten established HNSCC cell lines from the University of Michigan series (UM-SCC) was obtained from Dr. T. E. Carey at the University of Michigan, Ann Arbor, MI. The UM-SCC cell lines were derived from eight patients with SCC of the upper aerodigestive tract (supplemental Table 1). Patient age at tumor diagnosis ranged from 37 to 72 years. The cell lines selected were obtained from patients with stage I-IV tumors, distributed among oral, pharyngeal and laryngeal sites. All the patients had aggressive disease, with early recurrence and death within two years of therapy. Cell lines established from single isolates of a patient specimen are designated by a numeric designation, and where isolates from two time points or anatomical sites were obtained, the designation includes an alphabetical suffix (i.e., "A" or "B"). The cell lines were maintained in Eagle's minimal essential media supplemented with 10% fetal bovine serum and penicillin/streptomycin.
    [Show full text]
  • A Computational Approach for Defining a Signature of Β-Cell Golgi Stress in Diabetes Mellitus
    Page 1 of 781 Diabetes A Computational Approach for Defining a Signature of β-Cell Golgi Stress in Diabetes Mellitus Robert N. Bone1,6,7, Olufunmilola Oyebamiji2, Sayali Talware2, Sharmila Selvaraj2, Preethi Krishnan3,6, Farooq Syed1,6,7, Huanmei Wu2, Carmella Evans-Molina 1,3,4,5,6,7,8* Departments of 1Pediatrics, 3Medicine, 4Anatomy, Cell Biology & Physiology, 5Biochemistry & Molecular Biology, the 6Center for Diabetes & Metabolic Diseases, and the 7Herman B. Wells Center for Pediatric Research, Indiana University School of Medicine, Indianapolis, IN 46202; 2Department of BioHealth Informatics, Indiana University-Purdue University Indianapolis, Indianapolis, IN, 46202; 8Roudebush VA Medical Center, Indianapolis, IN 46202. *Corresponding Author(s): Carmella Evans-Molina, MD, PhD ([email protected]) Indiana University School of Medicine, 635 Barnhill Drive, MS 2031A, Indianapolis, IN 46202, Telephone: (317) 274-4145, Fax (317) 274-4107 Running Title: Golgi Stress Response in Diabetes Word Count: 4358 Number of Figures: 6 Keywords: Golgi apparatus stress, Islets, β cell, Type 1 diabetes, Type 2 diabetes 1 Diabetes Publish Ahead of Print, published online August 20, 2020 Diabetes Page 2 of 781 ABSTRACT The Golgi apparatus (GA) is an important site of insulin processing and granule maturation, but whether GA organelle dysfunction and GA stress are present in the diabetic β-cell has not been tested. We utilized an informatics-based approach to develop a transcriptional signature of β-cell GA stress using existing RNA sequencing and microarray datasets generated using human islets from donors with diabetes and islets where type 1(T1D) and type 2 diabetes (T2D) had been modeled ex vivo. To narrow our results to GA-specific genes, we applied a filter set of 1,030 genes accepted as GA associated.
    [Show full text]
  • Integrating Single-Step GWAS and Bipartite Networks Reconstruction Provides Novel Insights Into Yearling Weight and Carcass Traits in Hanwoo Beef Cattle
    animals Article Integrating Single-Step GWAS and Bipartite Networks Reconstruction Provides Novel Insights into Yearling Weight and Carcass Traits in Hanwoo Beef Cattle Masoumeh Naserkheil 1 , Abolfazl Bahrami 1 , Deukhwan Lee 2,* and Hossein Mehrban 3 1 Department of Animal Science, University College of Agriculture and Natural Resources, University of Tehran, Karaj 77871-31587, Iran; [email protected] (M.N.); [email protected] (A.B.) 2 Department of Animal Life and Environment Sciences, Hankyong National University, Jungang-ro 327, Anseong-si, Gyeonggi-do 17579, Korea 3 Department of Animal Science, Shahrekord University, Shahrekord 88186-34141, Iran; [email protected] * Correspondence: [email protected]; Tel.: +82-31-670-5091 Received: 25 August 2020; Accepted: 6 October 2020; Published: 9 October 2020 Simple Summary: Hanwoo is an indigenous cattle breed in Korea and popular for meat production owing to its rapid growth and high-quality meat. Its yearling weight and carcass traits (backfat thickness, carcass weight, eye muscle area, and marbling score) are economically important for the selection of young and proven bulls. In recent decades, the advent of high throughput genotyping technologies has made it possible to perform genome-wide association studies (GWAS) for the detection of genomic regions associated with traits of economic interest in different species. In this study, we conducted a weighted single-step genome-wide association study which combines all genotypes, phenotypes and pedigree data in one step (ssGBLUP). It allows for the use of all SNPs simultaneously along with all phenotypes from genotyped and ungenotyped animals. Our results revealed 33 relevant genomic regions related to the traits of interest.
    [Show full text]
  • The Legionella Kinase Legk7 Exploits the Hippo Pathway Scaffold Protein MOB1A for Allostery and Substrate Phosphorylation
    The Legionella kinase LegK7 exploits the Hippo pathway scaffold protein MOB1A for allostery and substrate phosphorylation Pei-Chung Leea,b,1, Ksenia Beyrakhovac,1, Caishuang Xuc, Michal T. Bonieckic, Mitchell H. Leea, Chisom J. Onub, Andrey M. Grishinc, Matthias P. Machnera,2, and Miroslaw Cyglerc,2 aDivision of Molecular and Cellular Biology, Eunice Kennedy Shriver National Institute of Child Health and Human Development, NIH, Bethesda, MD 20892; bDepartment of Biological Sciences, College of Liberal Arts and Sciences, Wayne State University, Detroit, MI 48202; and cDepartment of Biochemistry, University of Saskatchewan, Saskatoon, SK S7N5E5, Canada Edited by Ralph R. Isberg, Tufts University School of Medicine, Boston, MA, and approved May 1, 2020 (received for review January 12, 2020) During infection, the bacterial pathogen Legionella pneumophila Active LATS1/2 phosphorylate the cotranscriptional regulator manipulates a variety of host cell signaling pathways, including YAP1 (yes-associated protein 1) and its homolog TAZ (tran- the Hippo pathway which controls cell proliferation and differen- scriptional coactivator with PDZ-binding motif). Phosphorylated tiation in eukaryotes. Our previous studies revealed that L. pneu- YAP1 and TAZ are prevented from entering the nucleus by being mophila encodes the effector kinase LegK7 which phosphorylates either sequestered in the cytosol through binding to 14-3-3 pro- MOB1A, a highly conserved scaffold protein of the Hippo path- teins or targeted for proteolytic degradation (6, 8). Consequently, way. Here, we show that MOB1A, in addition to being a substrate the main outcome of signal transduction along the Hippo pathway of LegK7, also functions as an allosteric activator of its kinase is changes in gene expression (6).
    [Show full text]
  • Redefining the Specificity of Phosphoinositide-Binding by Human
    bioRxiv preprint doi: https://doi.org/10.1101/2020.06.20.163253; this version posted June 21, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC 4.0 International license. Redefining the specificity of phosphoinositide-binding by human PH domain-containing proteins Nilmani Singh1†, Adriana Reyes-Ordoñez1†, Michael A. Compagnone1, Jesus F. Moreno Castillo1, Benjamin J. Leslie2, Taekjip Ha2,3,4,5, Jie Chen1* 1Department of Cell & Developmental Biology, University of Illinois at Urbana-Champaign, Urbana, IL 61801; 2Department of Biophysics and Biophysical Chemistry, Johns Hopkins University School of Medicine, Baltimore, MD 21205; 3Department of Biophysics, Johns Hopkins University, Baltimore, MD 21218; 4Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21205; 5Howard Hughes Medical Institute, Baltimore, MD 21205, USA †These authors contributed equally to this work. *Correspondence: [email protected]. bioRxiv preprint doi: https://doi.org/10.1101/2020.06.20.163253; this version posted June 21, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC 4.0 International license. ABSTRACT Pleckstrin homology (PH) domains are presumed to bind phosphoinositides (PIPs), but specific interaction with and regulation by PIPs for most PH domain-containing proteins are unclear. Here we employed a single-molecule pulldown assay to study interactions of lipid vesicles with full-length proteins in mammalian whole cell lysates.
    [Show full text]
  • Identifying Host Genetic Factors Controlling Susceptibility to Blood-Stage Malaria in Mice
    Identifying host genetic factors controlling susceptibility to blood-stage malaria in mice Aurélie Laroque Department of Biochemistry McGill University Montreal, Quebec, Canada December 2016 A thesis submitted to McGill University in partial fulfilment of the requirements of the degree of Doctor of Philosophy. © Aurélie Laroque, 2016 ABSTRACT This thesis examines genetic factors controlling host response to blood stage malaria in mice. We first phenotyped 25 inbred strains for resistance/susceptibility to Plasmodium chabaudi chabaudi AS infection. A broad spectrum of responses was observed, which suggests rich genetic diversity among different mouse strains in response to malaria. A F2 intercross was generated between susceptible SM/J and resistant C57BL/6 mice and the progeny was phenotyped for susceptibility to P. chabaudi chabaudi AS infection. A whole genome scan revealed the Char1 locus as a key regulator of parasite density. Using a haplotype mapping approach, we reduced the locus to a 0.4Mb conserved interval that segregates with resistance/susceptibility to infection for the search of positional candidate genes. In addition, I pursued the work on the Char10 locus that was previously identified in [AcB62xCBA/PK]F2 animals (LOD=10.8, 95% Bayesian CI=50.7-75Mb). Pyruvate kinase deficiency was found to protect mice and humans against malaria. However, AcB62 mice are susceptible to P. chabaudi infection despite carrying the protective PklrI90N mutation. We characterized the Char10 locus and showed that it modulates the severity of the pyruvate deficiency phenotype by regulating erythroid responses. We created 4 congenic lines carrying different portions of the Char10 interval and demonstrated that Char10 is found within a maximal 4Mb interval.
    [Show full text]
  • MYC-Containing Amplicons in Acute Myeloid Leukemia: Genomic Structures, Evolution, and Transcriptional Consequences
    Leukemia (2018) 32:2152–2166 https://doi.org/10.1038/s41375-018-0033-0 ARTICLE Acute myeloid leukemia Corrected: Correction MYC-containing amplicons in acute myeloid leukemia: genomic structures, evolution, and transcriptional consequences 1 1 2 2 1 Alberto L’Abbate ● Doron Tolomeo ● Ingrid Cifola ● Marco Severgnini ● Antonella Turchiano ● 3 3 1 1 1 Bartolomeo Augello ● Gabriella Squeo ● Pietro D’Addabbo ● Debora Traversa ● Giulia Daniele ● 1 1 3 3 4 Angelo Lonoce ● Mariella Pafundi ● Massimo Carella ● Orazio Palumbo ● Anna Dolnik ● 5 5 6 2 7 Dominique Muehlematter ● Jacqueline Schoumans ● Nadine Van Roy ● Gianluca De Bellis ● Giovanni Martinelli ● 3 4 8 1 Giuseppe Merla ● Lars Bullinger ● Claudia Haferlach ● Clelia Tiziana Storlazzi Received: 4 August 2017 / Revised: 27 October 2017 / Accepted: 13 November 2017 / Published online: 22 February 2018 © The Author(s) 2018. This article is published with open access Abstract Double minutes (dmin), homogeneously staining regions, and ring chromosomes are vehicles of gene amplification in cancer. The underlying mechanism leading to their formation as well as their structure and function in acute myeloid leukemia (AML) remain mysterious. We combined a range of high-resolution genomic methods to investigate the architecture and expression pattern of amplicons involving chromosome band 8q24 in 23 cases of AML (AML-amp). This 1234567890();,: revealed that different MYC-dmin architectures can coexist within the same leukemic cell population, indicating a step-wise evolution rather than a single event origin, such as through chromothripsis. This was supported also by the analysis of the chromothripsis criteria, that poorly matched the model in our samples. Furthermore, we found that dmin could evolve toward ring chromosomes stabilized by neocentromeres.
    [Show full text]
  • Targeting PH Domain Proteins for Cancer Therapy
    The Texas Medical Center Library DigitalCommons@TMC The University of Texas MD Anderson Cancer Center UTHealth Graduate School of The University of Texas MD Anderson Cancer Biomedical Sciences Dissertations and Theses Center UTHealth Graduate School of (Open Access) Biomedical Sciences 12-2018 Targeting PH domain proteins for cancer therapy Zhi Tan Follow this and additional works at: https://digitalcommons.library.tmc.edu/utgsbs_dissertations Part of the Bioinformatics Commons, Medicinal Chemistry and Pharmaceutics Commons, Neoplasms Commons, and the Pharmacology Commons Recommended Citation Tan, Zhi, "Targeting PH domain proteins for cancer therapy" (2018). The University of Texas MD Anderson Cancer Center UTHealth Graduate School of Biomedical Sciences Dissertations and Theses (Open Access). 910. https://digitalcommons.library.tmc.edu/utgsbs_dissertations/910 This Dissertation (PhD) is brought to you for free and open access by the The University of Texas MD Anderson Cancer Center UTHealth Graduate School of Biomedical Sciences at DigitalCommons@TMC. It has been accepted for inclusion in The University of Texas MD Anderson Cancer Center UTHealth Graduate School of Biomedical Sciences Dissertations and Theses (Open Access) by an authorized administrator of DigitalCommons@TMC. For more information, please contact [email protected]. TARGETING PH DOMAIN PROTEINS FOR CANCER THERAPY by Zhi Tan Approval page APPROVED: _____________________________________________ Advisory Professor, Shuxing Zhang, Ph.D. _____________________________________________
    [Show full text]
  • Structural Basis for Autoinhibition and Its Relief of MOB1 in the Hippo
    www.nature.com/scientificreports OPEN Structural basis for autoinhibition and its relief of MOB1 in the Hippo pathway Received: 10 February 2016 Sun-Yong Kim, Yuka Tachioka, Tomoyuki Mori & Toshio Hakoshima Accepted: 03 June 2016 MOB1 protein is a key regulator of large tumor suppressor 1/2 (LATS1/2) kinases in the Hippo pathway. Published: 23 June 2016 MOB1 is present in an autoinhibited form and is activated by MST1/2-mediated phosphorylation, although the precise mechanisms responsible for autoinhibition and activation are unknown due to lack of an autoinhibited MOB1 structure. Here, we report on the crystal structure of full-length MOB1B in the autoinhibited form and a complex between the MOB1B core domain and the N-terminal regulation (NTR) domain of LATS1. The structure of full-length MOB1B shows that the N-terminal extension forms a short β-strand, the SN strand, followed by a long conformationally flexible positively-charged linker and α-helix, the Switch helix, which blocks the LATS1 binding surface of MOB1B. The Switch helix is stabilized by β-sheet formation of the SN strand with the S2 strand of the MOB1 core domain. Phosphorylation of Thr12 and Thr35 residues structurally accelerates dissociation of the Switch helix from the LATS1-binding surface by the “pull-the-string” mechanism, thereby enabling LATS1 binding. The Hippo pathway is a key signaling cascade that ensures organ size and normal tissue growth by coordinating cell proliferation and differentiation, and has now been recognized as an essential tumor suppressor cascade1–6. In mammals, the core pathway components comprise two Ser/Thr protein kinases, mammalian Ste20-like 1 and 2 (MST1/2) kinases, members of the Ste20 group in the germinal center kinase II (GCK-II) subgroup, and large tumor suppressor 1 and 2 (LATS1/2) kinases, members of the AGC protein kinase family, in addition to transcriptional co-activator Yes-associated protein (YAP) and transcriptional co-activator with PDZ-binding motif (TAZ).
    [Show full text]
  • Identification of Potential Key Genes and Pathway Linked with Sporadic Creutzfeldt-Jakob Disease Based on Integrated Bioinformatics Analyses
    medRxiv preprint doi: https://doi.org/10.1101/2020.12.21.20248688; this version posted December 24, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted medRxiv a license to display the preprint in perpetuity. All rights reserved. No reuse allowed without permission. Identification of potential key genes and pathway linked with sporadic Creutzfeldt-Jakob disease based on integrated bioinformatics analyses Basavaraj Vastrad1, Chanabasayya Vastrad*2 , Iranna Kotturshetti 1. Department of Biochemistry, Basaveshwar College of Pharmacy, Gadag, Karnataka 582103, India. 2. Biostatistics and Bioinformatics, Chanabasava Nilaya, Bharthinagar, Dharwad 580001, Karanataka, India. 3. Department of Ayurveda, Rajiv Gandhi Education Society`s Ayurvedic Medical College, Ron, Karnataka 562209, India. * Chanabasayya Vastrad [email protected] Ph: +919480073398 Chanabasava Nilaya, Bharthinagar, Dharwad 580001 , Karanataka, India NOTE: This preprint reports new research that has not been certified by peer review and should not be used to guide clinical practice. medRxiv preprint doi: https://doi.org/10.1101/2020.12.21.20248688; this version posted December 24, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted medRxiv a license to display the preprint in perpetuity. All rights reserved. No reuse allowed without permission. Abstract Sporadic Creutzfeldt-Jakob disease (sCJD) is neurodegenerative disease also called prion disease linked with poor prognosis. The aim of the current study was to illuminate the underlying molecular mechanisms of sCJD. The mRNA microarray dataset GSE124571 was downloaded from the Gene Expression Omnibus database. Differentially expressed genes (DEGs) were screened.
    [Show full text]
  • Whole Exome Sequencing in Families at High Risk for Hodgkin Lymphoma: Identification of a Predisposing Mutation in the KDR Gene
    Hodgkin Lymphoma SUPPLEMENTARY APPENDIX Whole exome sequencing in families at high risk for Hodgkin lymphoma: identification of a predisposing mutation in the KDR gene Melissa Rotunno, 1 Mary L. McMaster, 1 Joseph Boland, 2 Sara Bass, 2 Xijun Zhang, 2 Laurie Burdett, 2 Belynda Hicks, 2 Sarangan Ravichandran, 3 Brian T. Luke, 3 Meredith Yeager, 2 Laura Fontaine, 4 Paula L. Hyland, 1 Alisa M. Goldstein, 1 NCI DCEG Cancer Sequencing Working Group, NCI DCEG Cancer Genomics Research Laboratory, Stephen J. Chanock, 5 Neil E. Caporaso, 1 Margaret A. Tucker, 6 and Lynn R. Goldin 1 1Genetic Epidemiology Branch, Division of Cancer Epidemiology and Genetics, National Cancer Institute, NIH, Bethesda, MD; 2Cancer Genomics Research Laboratory, Division of Cancer Epidemiology and Genetics, National Cancer Institute, NIH, Bethesda, MD; 3Ad - vanced Biomedical Computing Center, Leidos Biomedical Research Inc.; Frederick National Laboratory for Cancer Research, Frederick, MD; 4Westat, Inc., Rockville MD; 5Division of Cancer Epidemiology and Genetics, National Cancer Institute, NIH, Bethesda, MD; and 6Human Genetics Program, Division of Cancer Epidemiology and Genetics, National Cancer Institute, NIH, Bethesda, MD, USA ©2016 Ferrata Storti Foundation. This is an open-access paper. doi:10.3324/haematol.2015.135475 Received: August 19, 2015. Accepted: January 7, 2016. Pre-published: June 13, 2016. Correspondence: [email protected] Supplemental Author Information: NCI DCEG Cancer Sequencing Working Group: Mark H. Greene, Allan Hildesheim, Nan Hu, Maria Theresa Landi, Jennifer Loud, Phuong Mai, Lisa Mirabello, Lindsay Morton, Dilys Parry, Anand Pathak, Douglas R. Stewart, Philip R. Taylor, Geoffrey S. Tobias, Xiaohong R. Yang, Guoqin Yu NCI DCEG Cancer Genomics Research Laboratory: Salma Chowdhury, Michael Cullen, Casey Dagnall, Herbert Higson, Amy A.
    [Show full text]