DOCSLIB.ORG

Abstract Light Shift Measurements of Cold

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Abstract Light Shift Measurements of Cold ABSTRACT LIGHT SHIFT MEASUREMENTS OF COLD RUBIDIUM ATOMS USING RAMAN PUMP-PROBE SPECTROSCOPY Nathan Jon Souther We have measured light shifts, also known as the A.C. Stark effect, in cold Rubidium atoms using pump-probe spectroscopy. The measurement was made both for atoms in a magneto optical trap (MOT) and for atoms that were in an optical molasses. We show that while the measured light shifts agree with theory for optical molasses there are additional Zeeman shifts in the MOT that the theory does not account for. To the best of our knowledge, this is the first time a careful systematic measurement has been performed in cold atoms of light shift as a function of intensity. LIGHT SHIFT MEASUREMENTS OF COLD RUBIDIUM ATOMS USING RAMAN PUMP-PROBE SPECTROSCOPY A Thesis Submitted to the Faculty of Miami University in partial fulfillment of the requirements for the degree of Master of Science Department of Physics by Nathan Jon Souther Miami University Oxford, Ohio 2009 Advisor Samir Bali Reader Bur¸cinBayram Reader James Clemens Reader Perry Rice TABLE OF CONTENTS List of Figures . iv Dedication . vi Acknowledgments . vii CHAPTER PAGE 1 Background and Motivation . 1 1.1 Organization of this Thesis . 3 2 Theory and Principles of Light Shift Measurement . 5 2.1 Magneto Optical Trap . 5 2.2 Doppler Cooling . 6 2.3 Trapping the Cooled Atoms in One Spot . 7 2.4 Sub-Doppler Cooling . 8 2.4.1 Motion Induced Atomic Orientation Cooling . 8 2.4.2 Sisyphus Cooling . 11 2.5 Light Shift for a Two Level Atom . 12 2.6 Simplified Light Shift Model for a Multi-Level Atom . 19 2.7 Expected Signal of Light Shift Measurement . 20 3 The Trapping and Repumper Systems . 26 3.1 The External Cavity Diode Laser . 26 3.2 Anamorphic Prism Pair . 28 3.3 Faraday Rotator . 29 3.4 Creating Six Trapping Beams . 33 3.5 Repumper Laser . 34 4 Locking the Lasers . 36 4.1 Saturated Absorption Set Up . 36 4.2 Lowering Threshold . 38 ii 4.3 Acousto Optical Modulator . 40 4.4 Locking the Trap Beam . 41 5 Frequency Scannable Probe . 47 5.1 Spectrum Analyzer . 52 6 The Vacuum System and Magnetic Field Considerations . 57 6.1 Vacuum System . 57 6.2 Canceling the Earth's Magnetic Field . 58 6.3 Applying Magnetic Gradient . 58 7 Experimental Procedure . 63 7.1 Preparation . 63 7.2 Data Collection, MOT . 64 7.3 Data Collection, Molasses . 66 8 Results and Discussion . 68 8.1 The Theoretical Prediction . 68 8.2 Molasses and MOT Data . 70 9 Conclusions and Future Outlook . 71 9.1 Conclusions . 71 9.2 Future Outlook . 71 9.2.1 Independent Pump-Probe . 72 9.3 Optical Fiber . 73 9.4 Independent Pump-Probe Measurements . 73 Bibliography . 78 iii LIST OF FIGURES FIGURE PAGE 2.1 Laser Cooling . 6 2.2 Atom Trapping . 8 2.3 Polarization Gradient for σ+ and σ− polarized Light . 9 2.4 Clebsch-Gordan Coefficients for J = 1 to J 0 = 2 Atomic System . 10 2.5 Motion Induced Population Imbalance . 11 2.6 Polarization Gradient and Energy Light Shift for π-polarized Light . 13 2.7 Clebsch-Gordan Coefficients for J=1/2 to J'=3/2 Atomic System . 14 2.8 Two Level Atom . 15 2.9 Ground State Light Shift . 18 2.10 Clebsch-Gordan Coefficients for the F=3 to F0= 4 Atomic System . 23 2.11 Light Shifts in the F=3 Ground State Atomic Levels . 24 2.12 Cause of Raman Peaks . 25 3.1 Trapping Beam Optical Layout . 27 3.2 Anamorphic Prism Pair Setup . 29 3.3 Anamorphic Prism Pair Angles . 30 3.4 Anamorphic Prism Pair Displacements . 31 4.1 Saturated Absorption Spectroscopy Setup . 37 4.2 Saturated Spectrum Hyperfine Ground State Pictures . 43 4.3 BNC Connections with Laser Locking Box . 44 4.4 Circuit for Creating Variable Fixed Offset for AOM . 45 iv 4.5 Locking Points for Different Detunings of Trap Laser . 46 5.1 Optical Layout for the Pump-Probe . 48 5.2 Circuit for Creating Variable Scanning Offset for AOM . 51 5.3 Double-pass AO Setup for Probe . 52 5.4 Single Pass Frequency Shift . 55 5.5 Double Pass Frequency Shift . 56 6.1 Getter Pin Diagram . 59 6.2 Magnetic Field Turn Off . 61 6.3 Magnetic Field Turn On . 62 7.1 Typical Light Shift Measurement . 65 7.2 Molasses Data Taking Timing . 67 8.1 MOT and Molasses Data . 69 9.1 Independent Pump Probe Setup . 72 9.2 Multi Mode vs. Single Mode Fibers . 74 9.3 Circuit Diagram for Pump Shutter Control . 75 9.4 Pump Shutter Opening . 76 9.5 Spectrum for Independent Pump-Probe . 77 9.6 Trap Shutter Closing . 77 v To Drea vi ACKNOWLEDGMENTS I would first like to thank my advisor Samir along with undergraduates Peter Harnish and Richard Wagner for all their work along side of me, including those 30 hour days in the lab. I would not have been able to accomplish what I have without their help. I am also indebted to Michael Eldridge and Mark Fisher. If it was not for Mike's helpfulness, expertise, and availability work in the lab would have been a lot slower. He was always able to make or help me make the pieces that I needed in the lab. Mark's helpfulness and ability to have random electronic components stored away on his shelves has proved invaluable and saved us a lot of time. I'm thankful for all the department faculty and staff that taught me and helped me in numerous ways, along with my fellow graduate students who provided me with entertainment, and especially those who provided used of their vehicles. Finally, I would like to thank my family for all the support they have given me over the years and Andrea for putting up with me being 700 miles away for two years. vii CHAPTER 1 BACKGROUND AND MOTIVATION A magneto optical trap (MOT) has become a standard tool in recent years, allowing for cold atomic samples in the micro Kelvin temperature range. Doppler broadening and collision rates in the MOT are greatly reduced. These properties make cold atoms an attractive environment to conduct fundamental experiments in atomic and optical physics. Since this setting has become so popular it is important to fully understand it. The use of pump-probe spectroscopy allows for diagnostic measurements of the MOT while still in operation. Due to the low powers used in the probe, the measure- ments are nondestructive allowing for continuous measurement of the behavior of the atom in the trap and the parameters of the trap. Pump-probe spectroscopy can also be used right after the atoms are released from the trap as is the case with optical molasses which are formed by turning off the magnetic field gradient in the MOT. Through a careful study of the MOT or molasseses new information is gained about the dynamics of the cold atoms. One particular area of interest is the exploration of Raman transitions that occur between the light shifted Zeeman sublevels of the trapped atoms. By exploring the correlation between the light shift and radiation pressure among the trapped atoms one group [1] has suggested using negative pressures to induce an optical implosion of trapped atoms. Grison et al. [2] was the first group to experimentally show, using a probe beam, the existence of population differences in 1 Zeeman ground state atomic sublevels. Another group [3] has studied the polarization dependence of the probe when performing spectroscopy of a MOT. The differences they found are signatures of optical anisotropy in the cold atoms. Our own motivation to study Raman spectroscopy of the light shifted Zeeman sublevels of the cold trapped atoms is threefold. First, since there are many schools with working MOTs, there is clearly a peda- gogical interest to demonstrate spectroscopy on a sub-MHz scale. Almost all MOT setups use saturated absorption techniques to lock the trapping lasers. Saturated Absorption offers a great introduction to atomic spectroscopy at the few MHz level to the advance undergraduate and graduate student. We show here that with the addition of a weak probe beam that can be scanned in frequency, a $30 photo diode detector, and a standard oscilloscope one can easily perform atomic spectroscopy with 0.01-0.1 MHz resolution. Second, upon scouring the literature we have found, to our surprise, no evidence of a systematic measurement of light shifts in cold atoms as a function of laser intensity. Several interesting questions arise: Many atomic groups use the MOT as a target for a variety of spectroscopic mea- surements [4], without feeling a need to instead use molasses (obtained by turning off the magnetic field gradient in the MOT). Molasses are colder and denser than the MOT, however the disadvantage is that molasses are transient, with the atoms diffusing away in a few hundred milliseconds. Hence, the question arises: While the MOT is a more convenient test-bed than molasses, is it possible at all to reliably measure light shifts in the MOT? How badly are these measurements affected by the presence of the magnetic field gradient? The traditional theoretical treatment of the light shift is based on a completely coherent light-atom interaction where spontaneous emission can be taken to be ab- sent. How well does this coherent theory compare with measurements performed on cold atoms trapped by near-resonant light? 2 Third, our immediate goal is to build an optical lattice for the purpose of studying anomalous atomic transport that has been predicted in near-resonant lattices.
Load more

Recommended publications
  • Comparison of Gravitational and Light Frequency Shifts in Rubidium Atomic Clock
    universe Communication Comparison of Gravitational and Light Frequency Shifts in Rubidium Atomic Clock Alexey Baranov, Sergey Ermak *, Roman Lozov and Vladimir Semenov The Institute of Physics, Nanotechnology and Telecommunications, Peter the Great St. Petersburg Polytechnic University, 195251 Saint Petersburg, Russia; [email protected] (A.B.); [email protected] (R.L.); [email protected] (V.S.) * Correspondence: [email protected]; Tel.: +7-921-791-9091 Abstract: The article presents the results of an experimental study of the external magnetic field orientation and magnitude influence on the rubidium atomic clock, simulating the influence of the geomagnetic field on the onboard rubidium atomic clock of navigation satellites. The tensor component value of the atomic clock frequency light shift on the rubidium cell was obtained, and this value was ∼2 Hz. The comparability of the relative light shift (∼10−9) and the regular gravitational correction 4 × 10−10 to the frequency of the rubidium atomic clock was shown. The experimental results to determine the orientational shift influence on the rubidium atomic clock frequency were presented. A significant effect on the relative frequency instability of a rubidium atomic clock at a level of 10−12 10−13 for rotating external magnetic field amplitudes of 1.5 A/m and 3 A/m was demonstrated. This magnitude corresponds to the geomagnetic field in the orbit of navigation satellites. The necessity of taking into account various factors (satellite orbit parameters and atomic clock characteristics) is substantiated for correct comparison of corrections to the rubidium onboard atomic clock frequency associated with the Earth’s gravitational field action and the satellite orientation in the geomagnetic field.
    [Show full text]
  • Polarization Squeezing of Light by Single Passage Through an Atomic Vapor
    PHYSICAL REVIEW A 84, 033851 (2011) Polarization squeezing of light by single passage through an atomic vapor S. Barreiro, P. Valente, H. Failache, and A. Lezama* Instituto de F´ısica, Facultad de Ingenier´ıa, Universidad de la Republica,´ J. Herrera y Reissig 565, 11300 Montevideo, Uruguay (Received 8 June 2011; published 28 September 2011) We have studied relative-intensity fluctuations for a variable set of orthogonal elliptic polarization components of a linearly polarized laser beam traversing a resonant 87Rb vapor cell. Significant polarization squeezing at the threshold level (−3dB) required for the implementation of several continuous-variable quantum protocols was observed. The extreme simplicity of the setup, which is based on standard polarization components, makes it particularly convenient for quantum information applications. DOI: 10.1103/PhysRevA.84.033851 PACS number(s): 42.50.Ct, 42.50.Dv, 32.80.Qk, 42.50.Lc In recent years, significant attention has been given to vapor cell results in squeezing of the polarization orthogonal to the use of continuous variables for quantum information that of the pump (vacuum squeezing) [14–17] as a consequence processing. A foreseen goal is the distribution of entanglement of the nonlinear optical mechanism known as polarization self- between distant nodes. For this, quantum correlated light rotation (PSR) [18–20]. Vacuum squeezing via PSR has been 87 beams are to interact with separate atomic systems in order observed for the D1 [15–17] and D2 [14] transitions using Rb to build quantum mechanical correlations between them [1,2]. vapor. As noted in [9], the existence of polarization squeezing A particular kind of quantum correlation between two light can be inferred from these results.
    [Show full text]
  • Multichannel Cavity Optomechanics for All-Optical Amplification of Radio Frequency Signals
    ARTICLE Received 6 Jul 2012 | Accepted 30 Aug 2012 | Published 2 Oct 2012 DOI: 10.1038/ncomms2103 Multichannel cavity optomechanics for all-optical amplification of radio frequency signals Huan Li1, Yu Chen1, Jong Noh1, Semere Tadesse1 & Mo Li1 Optomechanical phenomena in photonic devices provide a new means of light–light interaction mediated by optical force actuated mechanical motion. In cavity optomechanics, this interaction can be enhanced significantly to achieve strong interaction between optical signals in chip-scale systems, enabling all-optical signal processing without resorting to electro-optical conversion or nonlinear materials. However, current implementation of cavity optomechanics achieves both excitation and detection only in a narrow band at the cavity resonance. This bandwidth limitation would hinder the prospect of integrating cavity optomechanical devices in broadband photonic systems. Here we demonstrate a new configuration of cavity optomechanics that includes two separate optical channels and allows broadband readout of optomechanical effects. The optomechanical interaction achieved in this device can induce strong but controllable nonlinear effects, which can completely dominate the device’s intrinsic mechanical properties. Utilizing the device’s strong optomechanical interaction and its multichannel configuration, we further demonstrate all-optical, wavelength- multiplexed amplification of radio-frequency signals. 1 Department of Electrical and Computer Engineering, University of Minnesota, Minneapolis, Minnesota
    [Show full text]
  • Turf-Times Der Deutsche Newsletter Für Vollblutzucht & Rennsport Mit Dem Galopp-Portal Unter
    Ausgabe 269 • 36 Seiten Freitag, 14. Juni 2013 powered by TURF-TIMES www.bbag-sales.de Der deutsche Newsletter für Vollblutzucht & Rennsport mit dem Galopp-Portal unter www.turf-times.de AUFGALOPP Probably läuft im Derby „Next stop German Derby“ lautete die Nachricht, die Die Bilder, die wir in den vergangenen Tagen in uns Trainer Rune Haugen am Mittwoch aus Norwe- den Medien gesehen haben, werden so schnell nicht gen bezüglich des von ihm betreuten Probably (Da- vergessen werden. Überschwemmte Landschaften, nehill Dancer) übermittelte. Damit wird das Sparda Menschen, die ihr Hab und Gut verloren haben, die 144. Deutsche Derby in jedem Fall international. Im vor den Trümmern ihrer Existenz stehen. Der Ga- vergangenen Jahr wurde der Hengst noch von David lopprennsport hat in der tagesaktuellen Berichter- Wachman für die Besitzergemeinschaft Tabor/Mag- stattung naturgemäß überhaupt keine Rolle gespielt, nier/Smith trainiert, gewann die Railway Stakes (Gr. auch wenn es zwei Rennbahnen betroffen hat, Halle II), war u.a. Dritter in den Beresford Stakes (Gr. II) und Magdeburg, nicht zum ersten Mal. Ausgerech- und Vierter in den National Stakes (Gr. I) in aller- net. Bahnen, die ohnehin nicht gerade mit Reichtum dings stets kleinen Feldern, über Winter wurde er an gesegnet sind, deren Überleben in der Vergangenheit den Stall NOR verkauft. Beim Jahresdebut belegte des Öfteren am seidenen Faden gehangen hat, denen er sieben Längen hinter Nicolosio (Peintre Celebre) schon mehrfach die Existenzberechtigung abgespro- Rang zwei im Derby-Trial in Hannover. Am Dienstag chen wurde, weil sie wirtschaftlich angeblich nicht gewann er im schwedischen Jägersro ein übersichtlich tragfähig sind. Doch wo in diesen Tagen trotzdem besetztes 2400-m-Rennen als 11:10-Favorit mit 22 Menschen arbeiten und alles erdenklich mögliche Längen Vorsprung.
    [Show full text]
  • Rydberg Excitation of Single Atoms for Applications in Quantum Information and Metrology Aaron Hankin
    University of New Mexico UNM Digital Repository Physics & Astronomy ETDs Electronic Theses and Dissertations 1-28-2015 Rydberg Excitation of Single Atoms for Applications in Quantum Information and Metrology Aaron Hankin Follow this and additional works at: https://digitalrepository.unm.edu/phyc_etds Recommended Citation Hankin, Aaron. "Rydberg Excitation of Single Atoms for Applications in Quantum Information and Metrology." (2015). https://digitalrepository.unm.edu/phyc_etds/23 This Dissertation is brought to you for free and open access by the Electronic Theses and Dissertations at UNM Digital Repository. It has been accepted for inclusion in Physics & Astronomy ETDs by an authorized administrator of UNM Digital Repository. For more information, please contact [email protected]. Aaron Hankin Candidate Physics and Astronomy Department This dissertation is approved, and it is acceptable in quality and form for publication: Approved by the Dissertation Committee: Ivan Deutsch , Chairperson Carlton Caves Keith Lidke Grant Biedermann Rydberg Excitation of Single Atoms for Applications in Quantum Information and Metrology by Aaron Michael Hankin B.A., Physics, North Central College, 2007 M.S., Physics, Central Michigan Univeristy, 2009 DISSERATION Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy Physics The University of New Mexico Albuquerque, New Mexico December 2014 iii c 2014, Aaron Michael Hankin iv Dedication To Maiko and our unborn daughter. \There are wonders enough out there without our inventing any." { Carl Sagan v Acknowledgments The experiment detailed in this manuscript evolved rapidly from an empty lab nearly four years ago to its current state. Needless to say, this is not something a graduate student could have accomplished so quickly by him or herself.
    [Show full text]
  • Travis Dissertation
    Experimental Generation and Manipulation of Quantum Squeezed Vacuum via Polarization Self-Rotation in Rb Vapor Travis Scott Horrom Scaggsville, MD Master of Science, College of William and Mary, 2010 Bachelor of Arts, St. Mary’s College of Maryland, 2008 A Dissertation presented to the Graduate Faculty of the College of William and Mary in Candidacy for the Degree of Doctor of Philosophy Department of Physics The College of William and Mary May 2013 c 2013 Travis Scott Horrom All rights reserved. APPROVAL PAGE This Dissertation is submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy Travis Scott Horrom Approved by the Committee, March, 2013 Committee Chair Research Assistant Professor Eugeniy E. Mikhailov, Physics The College of William and Mary Associate Professor Irina Novikova, Physics The College of William and Mary Assistant Professor Seth Aubin, Physics The College of William and Mary Professor John B. Delos, Physics The College of William and Mary Professor and Eminent Scholar Mark D. Havey, Physics Old Dominion University ABSTRACT Nonclassical states of light are of increasing interest due to their applications in the emerging field of quantum information processing and communication. Squeezed light is such a state of the electromagnetic field in which the quantum noise properties are altered compared with those of coherent light. Squeezed light and squeezed vacuum states are potentially useful for quantum information protocols as well as optical measurements, where sensitivities can be limited by quantum noise. We experimentally study a source of squeezed vacuum resulting from the interaction of near-resonant light with both cold and hot Rb atoms via the nonlinear polarization self-rotation effect (PSR).
    [Show full text]
  • Optical Binding with Cold Atoms
    Optical binding with cold atoms C. E. M´aximo,1 R. Bachelard,1 and R. Kaiser2 1Instituto de F´ısica de S~aoCarlos, Universidade de S~aoPaulo, 13560-970 S~aoCarlos, SP, Brazil 2Universit´eC^oted'Azur, CNRS, INPHYNI, 06560 Valbonne, France (Dated: November 16, 2017) Optical binding is a form of light-mediated forces between elements of matter which emerge in response to the collective scattering of light. Such phenomenon has been studied mainly in the context of equilibrium stability of dielectric spheres arrays which move amid dissipative media. In this letter, we demonstrate that optically bounded states of a pair of cold atoms can exist, in the absence of non-radiative damping. We study the scaling laws for the unstable-stable phase transition at negative detuning and the unstable-metastable one for positive detuning. In addition, we show that angular momentum can lead to dynamical stabilisation with infinite range scaling. The interaction of light with atoms, from the micro- pairs and discuss the increased range of such a dynami- scopic to the macroscopic scale, is one of the most fun- cally stabilized pair of atoms. damental mechanisms in nature. After the advent of the laser, new techniques were developed to manipulate pre- cisely objects of very different sizes with light, ranging from individual atoms [1] to macrosopic objects in opti- cal tweezers [2]. It is convenient to distinguish two kinds of optical forces which are of fundamental importance: the radiation pressure force, which pushes the particles in the direction of the light propagation, and the dipole force, which tends to trap them into intensity extrema, as for example in optical lattices.
    [Show full text]
  • Phase Steps and Resonator Detuning Measurements in Microresonator Frequency Combs
    ARTICLE Received 23 May 2014 | Accepted 27 Oct 2014 | Published 7 Jan 2015 DOI: 10.1038/ncomms6668 Phase steps and resonator detuning measurements in microresonator frequency combs Pascal Del’Haye1, Aure´lien Coillet1, William Loh1, Katja Beha1, Scott B. Papp1 & Scott A. Diddams1 Experiments and theoretical modelling yielded significant progress toward understanding of Kerr-effect induced optical frequency comb generation in microresonators. However, the simultaneous Kerr-mediated interaction of hundreds or thousands of optical comb frequencies with the same number of resonator modes leads to complicated nonlinear dynamics that are far from fully understood. An important prerequisite for modelling the comb formation process is the knowledge of phase and amplitude of the comb modes as well as the detuning from their respective microresonator modes. Here, we present comprehensive measurements that fully characterize optical microcomb states. We introduce a way of measuring resonator dispersion and detuning of comb modes in a hot resonator while generating an optical frequency comb. The presented phase measurements show unpredicted comb states with discrete p and p/2 steps in the comb phases that are not observed in conventional optical frequency combs. 1 National Institute of Standards and Technology (NIST), Boulder, Colorado 80305, USA. Correspondence and requests for materials should be addressedto P.D. (email: [email protected]). NATURE COMMUNICATIONS | 6:5668 | DOI: 10.1038/ncomms6668 | www.nature.com/naturecommunications 1 & 2015 Macmillan Publishers Limited. All rights reserved. ARTICLE NATURE COMMUNICATIONS | DOI: 10.1038/ncomms6668 ptical frequency combs have proven to be powerful a liquid crystal array-based waveshaper that allows independent metrology tools for a variety of applications, as well as for control of both the phase and amplitude of each comb mode.
    [Show full text]
  • Scandinavian Open Yearling Sale 2021
    2021 Friday tFhreid1a1tyh tohfeS 1e7pthte omf bSerp2te0m20beart 2130:2010 aht r1s3.:a0t0Y horrsk. Satu Ytoterkri Stutteri ScScandandinavinavianian Open Open YeaYearlingrling Sale Sale Organizer:Organizer: Dansk GalopDansk Galop 10101_DG_Forside_Aaring17_210x148_310717.indd10101_DG_Forside_Aaring17_210x148_310717.indd 1 1 01/08/2017 08.5701/08/2017 08.57 INDEX Information 4 Auktionsløb 2021 5 Conditions of sale 13 Auktionsvilkår 15 Criteria for use for of Black Type 17 Entries by consignors 19 Yearlings 22 Sire references 24 TIMETABLE Lot 1 13.00 hrs. Lot 20 apx. 14.00 Lot 40 apx. 15.00 Lot 60 apx. 16.00 Lot 80 apx. 17.00 Information contained in the catalogue is updated as per the 31st of July. The organizers are not responsible for any mistakes or ommissions. DANSK GALOP The Danish Jockey Club Dansk Galop (Foreningen til den ædle Hesteavls Fremme) is racing’s highest authority. The purpose of the organization is to promote thoroughbred breeding in Denmark and to lead Danish horse racing. The organization has app. 300 members and is led by a board of 15 members who represent racecourses, breeders, owners and trainers. Board of Directors: Nick Elsass (chairman), Mogens Schougaard (vice-chairman), Charlotte Brasch Andersen, Tine Hansen, Peter Haugaard, Stine Julø, Peter Leth Keller, Gert Larsen, Jens D. Lauritzen, Carsten Baagøe Schou, Peter Rolin, Iben Hjorth Buskop, Henrik Stork, Asbjørn Sørensen and Bente Østergaard. CEO: Peter Knudsen Traverbanevej 10, 2920 Charlottenlund Tel. (45) 88 81 12 13 – [email protected] www.danskgalop.dk / www.yearlingsale.dk 3 INFORMATION At the moment, the sales can be conducted without the restrictions experienced last year. However carefulness is strongly advised.
    [Show full text]
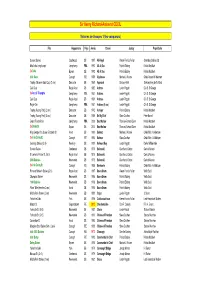
  • Palmarès Cecil
    Sir Henry Richard-Amherst CECIL Victoires de Groupes 1 (les vainqueurs) Prix Hippodrome Pays Année Cheval Jockey Propriétaire Sussex Stakes Goodwood GB 1997 Ali-Royal Kieren-Francis Fallon Greenbay Stables Ltd Moulin de Longchamp Longchamp FRA 1992 All At Sea Patrick Eddery Khalid Abdullah 2e Oaks Epsom GB 1992 All At Sea Patrick Eddery Khalid Abdullah Irish Oaks Curragh IRE 1989 Alydaress Michael J. Kinane Cheik Ahmed Al Maktoum Trophy (Observer Gold Cup) (2 ans) Doncaster GB 1969 Approval Duncan Keith Sir Humphrey de Trafford Gold Cup Royal Ascot GB 1982 Ardross Lester Piggott C.A.B. St George 2e Arc de Triomphe Longchamp FRA 1982 Ardross Lester Piggott C.A.B. St George Gold Cup Royal Ascot GB 1981 Ardross Lester Piggott C.A.B. St George Royal-Oak Longchamp FRA 1981 Ardross (5 ans) Lester Piggott C.A.B. St George Trophy (Racing Post) (2 ans) Doncaster GB 1992 Armiger Patrick Eddery Khalid Abdullah Trophy (Racing Post) (2 ans) Doncaster GB 1989 Be My Chief Steve Cauthen Peter Burrell Grand Prix de Paris Longchamp FRA 2000 Beat Hollow Thomas-Richard Quinn Khalid Abdullah 3e Derby St. Epsom GB 2000 Beat Hollow Thomas-Richard Quinn Khalid Abdullah King George VI & Queen Elizabeth St. Ascot GB 1990 Belmez Michael J. Kinane Cheik Moh. Al Maktoum 3e Irish Derby St. Curragh IRE 1990 Belmez Steve Cauthen Cheik Moh. Al Maktoum Lockinge Stakes (Gr.II) Newbury GB 1981 Belmont Bay Lester Piggott Daniel Wildenstein Sussex Stakes Goodwood GB 1975 Bolkonski Gianfranco Dettori Carlo d'Alessio St James's Palace St. (Gr.II) Royal Ascot GB 1975 Bolkonski Gianfranco Dettori Carlo d'Alessio 2000 Guinées Newmarket GB 1975 Bolkonski Gianfranco Dettori Carlo d'Alessio 2e Irish Derby St.
    [Show full text]
  • Exploring Theater As a Vehicle for Change, Inspired by the Poetic Performances of Ancient Andalucía
    MY HEART IS IN THE EAST: EXPLORING THEATER AS A VEHICLE FOR CHANGE, INSPIRED BY THE POETIC PERFORMANCES OF ANCIENT ANDALUCÍA JESSICA LITWAK A DISSERTATION Submitted to the Ph.D. in Leadership and Change Program of Antioch University in partial fulfillment of the requirements for the degree of Doctor of Philosophy May, 2015 This is to certify that the Dissertation entitled: MY HEART IS IN THE EAST: EXPLORING THEATER AS A VEHICLE FOR CHANGE, INSPIRED BY THE POETIC PERFORMANCES OF ANCIENT ANDALUCÍA prepared by Jessica Litwak is approved in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Leadership and Change Approved by: Carolyn Kenny, Ph.D., Chair date Elizabeth Holloway, Ph.D., Committee Member date D. Soyini Madison, Ph.D., Committee Member date Dara Culhane, Ph.D., Committee Member date Magdalena Kazubowski-Houston, Ph.D., External Reader date Copyright 2015 Jessica Litwak All rights reserved Acknowledgments No theater project is ever created or produced out by one person. No scholarly work comes out of one mind. No community action is a solo endeavor. The following people have believed in my vision and have edged me toward the completion of this project through many challenges. Their support emotionally, intellectually, and artistically enabled this dissertation to reach fruition. Dr. Carolyn Kenny—A sword in the clouds, an iron orchid, a compassionate warrior and a mother lion, Carolyn was my North Star, my Sherpa, my champion, and my challenger. Without her guidance, this dissertation simply would not have been conceived, written, and finished. During hours of doubt or darkness she offered hope in the form of scholarly articles, poems, stories, parables, gentle scolding, and vigorous pep talks.
    [Show full text]
  • Derby Double for Frankel As Hurricane Lane Swoops
    SUNDAY, 27 JUNE 2021 DERBY DOUBLE FOR SANTA BARBARA TO THE TEST IN PRETTY POLLY FRANKEL AS HURRICANE There have been valid excuses for her missing the target so far in 2021, but Sunday=s G1 Alwasmiyah Pretty Polly S. at The LANE SWOOPS Curragh offers the ideal opportunity for >TDN Rising Star= Santa Barbara (Ire) (Camelot {GB}) to deliver on her promise. Lacking vital experience when fourth in the G1 1000 Guineas at Newmarket May 2 she was probably undone by a combination of a 12-furlong trip and testing ground when fifth in the June 4 G1 Epsom Oaks. AShe clearly ran a hugely promising race for a horse coming off the back of just a maiden win when fourth in the Guineas and that was always going to be a big ask for her over a mile on fast ground in a Classic first time up,@ Ryan Moore commented. AIt looks like the trip proved beyond her in bad conditions when fifth in the Oaks last time, so this 10-furlong trip could prove her optimum. Hopefully she can take a step forward here, but she is up against some horses of a similar ability and in some cases higher-rated opposition so this is another tough Group 1 assignment for her.@ Cont. p10 Hurricane Lane (right) | Racingfotos.com It was a Derby double for Frankel (GB) on Saturday as Godolphin=s Hurricane Lane (Ire) stepped forward to emulate his stablemate Adayar (Ire) in flying the flag for his sire in The Curragh=s G1 Dubai Duty Free Irish Derby.
    [Show full text]