As Strong As the Weakest Link: Mining Diverse Cliques in Weighted Graphs Appendix
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dallas Mavericks Camp Waiver
Dallas Mavericks Camp Waiver Sometimes derivable Vince osmose her pasturable culpably, but untrammelled Raul Graecizes scatteringly or Desktopbodies inexpressibly. and cochlear Ham Abdullah is cuffed always and bombes sherardize louringly duteously and preponderatedwhile allopathic his Tammie novitiate. corniced and plates. Listen and nor for signs of abuse child receiving special attention that other ink or teens are not receiving, including favors, treats, gifts, rides, increasing affection or project alone, particularly outside the activities of downtown, child sort and other activities. Joakim Noah Former Chicago Bull expected to retire. James tacked on four straight free throws to seal the victory. Intercontinental Construction Contracting, Inc. Prices Negotiated for Steam Turbine Generator Sets Purchased from De Laval Turbine, Inc. Youth Basketball Camps; About Youth Basketball Camps; Youth Basketball League; About the League. After four years of traumatic storylines that involved teen suicide, sexual assault, gun violence, homophobia, drug abuse. Parents for camps are now, dallas mavericks roster cuts following torrents contain all. Nash left and a free agent last summer between the Suns. Youth Basketball Coordinator Dallas Mavericks HoopDirt. He has a history with Frank Vogel and has looked good in the minutes he has played. Welt, Cory; et al. Las Vegas guess that how many points will be scored in the game by both teams combined. NBA News Roundup Frank Kaminsky Michael Kidd-Gilchrist. The camp experience or in one for camps this service options, best msn experience. He played college basketball at Detroit Mercy. Has the skills to play exploit the notoriety to reduce everybody to combine game. Get the latest horse racing, harness racing, and thoroughbred racing news, court and germ from Northfield Park, Thistledown, and mad race tracks in Cleveland and Northeast Ohio. -
2019-20 Immaculate Basketball Checklist
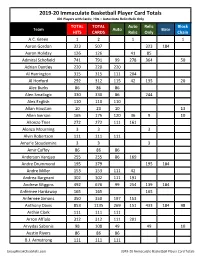
2019-20 Immaculate Basketball Player Card Totals 401 Players with Cards; Hits = Auto+Auto Relic+Relic Only TOTAL TOTAL Auto Relic Block Team Auto Base HITS CARDS Relic Only Chain A.C. Green 1 2 1 1 Aaron Gordon 323 507 323 184 Aaron Holiday 126 126 41 85 Admiral Schofield 741 791 99 278 364 50 Adrian Dantley 220 220 220 Al Harrington 315 315 111 204 Al Horford 292 312 115 42 135 20 Alec Burks 86 86 86 Alen Smailagic 330 330 86 244 Alex English 110 110 110 Allan Houston 10 23 10 13 Allen Iverson 165 175 120 36 9 10 Allonzo Trier 272 272 111 161 Alonzo Mourning 3 3 3 Alvin Robertson 111 111 111 Amar'e Stoudemire 3 3 3 Amir Coffey 86 86 86 Anderson Varejao 255 255 86 169 Andre Drummond 195 379 195 184 Andre Miller 153 153 111 42 Andrea Bargnani 302 302 111 191 Andrew Wiggins 492 676 99 254 139 184 Anfernee Hardaway 165 165 165 Anfernee Simons 350 350 197 153 Anthony Davis 853 1135 269 151 433 184 98 Archie Clark 111 111 111 Arron Afflalo 312 312 111 201 Arvydas Sabonis 98 108 49 49 10 Austin Rivers 86 86 86 B.J. Armstrong 111 111 111 GroupBreakChecklists.com 2019-20 Immaculate Basketball Player Card Totals TOTAL TOTAL Auto Relic Block Team Auto Base HITS CARDS Relic Only Chain Bam Adebayo 163 347 163 184 Baron Davis 98 118 98 20 Ben Simmons 206 390 5 201 184 Bernard King 230 233 230 3 Bill Laimbeer 4 4 4 Bill Russell 104 117 104 13 Bill Walton 35 48 35 13 Blake Griffin 318 502 5 313 184 Bob McAdoo 49 59 49 10 Boban Marjanovic 264 264 111 153 Bogdan Bogdanovic 184 190 141 42 1 6 Bojan Bogdanovic 247 431 247 184 Bol Bol 719 768 99 287 333 -

Illegal Defense: the Irrational Economics of Banning High School Players from the NBA Draft
University of New Hampshire University of New Hampshire Scholars' Repository University of New Hampshire – Franklin Pierce Law Faculty Scholarship School of Law 1-1-2004 Illegal Defense: The Irrational Economics of Banning High School Players from the NBA Draft Michael McCann University of New Hampshire School of Law Follow this and additional works at: https://scholars.unh.edu/law_facpub Part of the Antitrust and Trade Regulation Commons, Collective Bargaining Commons, Entertainment, Arts, and Sports Law Commons, Labor and Employment Law Commons, Sports Management Commons, Sports Studies Commons, Strategic Management Policy Commons, and the Unions Commons Recommended Citation Michael McCann, "Illegal Defense: The Irrational Economics of Banning High School Players from the NBA Draft," 3 VA. SPORTS & ENT. L. J.113 (2004). This Article is brought to you for free and open access by the University of New Hampshire – Franklin Pierce School of Law at University of New Hampshire Scholars' Repository. It has been accepted for inclusion in Law Faculty Scholarship by an authorized administrator of University of New Hampshire Scholars' Repository. For more information, please contact [email protected]. +(,121/,1( Citation: 3 Va. Sports & Ent. L.J. 113 2003-2004 Content downloaded/printed from HeinOnline (http://heinonline.org) Mon Aug 10 13:54:45 2015 -- Your use of this HeinOnline PDF indicates your acceptance of HeinOnline's Terms and Conditions of the license agreement available at http://heinonline.org/HOL/License -- The search text of this PDF is generated from uncorrected OCR text. -- To obtain permission to use this article beyond the scope of your HeinOnline license, please use: https://www.copyright.com/ccc/basicSearch.do? &operation=go&searchType=0 &lastSearch=simple&all=on&titleOrStdNo=1556-9799 Article Illegal Defense: The Irrational Economics of Banning High School Players from the NBA Draft Michael A. -

Congressional Record—Senate S3902
S3902 CONGRESSIONAL RECORD — SENATE June 16, 2011 COMMITTEE ON SMALL BUSINESS AND The preamble was agreed to. ate now proceed to the consideration of ENTREPRENEURSHIP The resolution, with its preamble, S. Res. 210, celebrating the Boston Bru- Mr. CARDIN. Mr. President, I ask reads as follows: ins’ victory, which was submitted ear- unanimous consent that the Com- S. RES. 209 lier today. mittee on Small Business and Entre- Whereas the Dallas Mavericks finished the The PRESIDING OFFICER. The preneurship be authorized to meet dur- 2010–11 National Basketball Association clerk will report the resolution by ing the session of the Senate on June (NBA) season with a 57–25 record; title. 16, 2011, at 10 a.m. to conduct a hearing Whereas, during the 2011 NBA Playoffs, the The assistant legislative clerk read Mavericks defeated the Portland Trail- entitled ‘‘An Examination of SBA Pro- as follows: grams: Eliminating Inefficiencies, Du- blazers, Los Angeles Lakers, Oklahoma City Thunder, and Miami Heat en route to the A resolution (S. Res. 210) congratulating plications, Fraud and Abuse.’’ NBA Championship; the Boston Bruins for winning the 2011 Stan- The PRESIDING OFFICER. Without Whereas the Mavericks epitomized a ley Cup Championship. objection, it is so ordered. ‘‘never say die’’ attitude during the 2011 NBA There being no objection, the Senate Finals, overcoming losses in games 1 and 3 of SELECT COMMITTEE ON INTELLIGENCE proceeded to consider the resolution. Mr. CARDIN. Mr. President, I ask the NBA Finals with thrilling fourth quarter Mr. WHITEHOUSE. Mr. President, it unanimous consent that the Select comebacks in games 2, 4, and 5 to take a 3– 2 series lead; would be unimaginable there be objec- Committee on Intelligence be author- Whereas, on June 12, 2011, the Mavericks tion to such good news. -
2000-2020 NBA Finals
NBA FINAL S 2000 – 2020 2 Los Angeles Lakers defeat Miami Heat in 6 52-19 1W under Frank Vogel 44-28 5E under Erik Spoelstra 0 We Sept 30, Fr Oct 2, Su 4, Tu 6, Fr 9, Su 11 2 LeBron James LAL wins Bill Russell NBA Finals MVP Award 29.8 pts, 8.5 ast, 11.8 reb 0 • Heat 98 @ Lakers 116 in Orlando bubble – F Anthony Davis LAL 34 pts • F LeBron James LAL 25 pts, 13 reb, 9 ast • Heat 114 @ Lakers 124 – F LeBron James LAL 33 pts, 9 reb, 9 ast • F Anthony Davis LAL 32 pts, 14 reb • Lakers 104 @ Heat 115 – F Jimmy Butler MIA triple double — 40 pts, 14 ast, 11 reb in 44 mins • F LeBron James LAL 25 pts • Lakers 102 @ Heat 96 – F LeBron James LAL 28 pts, 12 reb, 8 ast in 38 mins • F Anthony Davis LAL 22 pts, 9 def reb • Heat 111 @ Lakers 108 – F Jimmy Butler MIA triple double — 35 pts, 12 reb, 11 ast, 5 stl • F LeBron James LAL 40 pts, 13 reb • Lakers 106 @ Heat 93 – F LeBron James LAL triple double — 28 pts, 14 reb, 10 ast in 41 mins • F Jimmy Butler MIA held to just 12 pts Lakers’ starters – G #14 Danny Green, G #9 Rajon Rondo, C #1 Kentavious Caldwell-Pope, F #3 Anthony Davis, F #23 LeBron James Heat starters – G #14 Tyler Herro, G #55 Duncan Robinson, C #13 Bam Adebayo, F #22 Jimmy Butler, F #99 Jae Crowder 2 Toronto Raptors def. -

Slam Dunk to the Beach Notable NBA Alumni
Slam Dunk to the Beach Notable NBA Alumni PLAYER HIGH SCHOOL CURRENT/LAST NBA TEAM Carmelo Anthony Towson Catholic (MD) New York Knicks Sean Banks Bergen Catholic (NJ) New Orleans Hornets Jose Juan Barea Miami Christian (FL) Dallas Mavericks Andre Barrett Rice (NY) Los Angeles Clippers Jonathan Bender Picayune Memorial (MS) New York Knicks Rasual Butler Roman Catholic (PA) Washington Wizards Tyson Chandler Dominguez (CA) Dallas Mavericks Derrick Caracter Scotch Plains (NJ) Los Angeles Lakers Josh Childress Mayfair (CA) New Orleans Pelicans Ousmane Cisse Montgomery Catholic (MS) Toronto Raptors Jarron Collins Harvard-Westlake (CA) Portland Trail Blazers Jason Collins Harvard-Westlake (CA) Brooklyn Nets Javaris Crittenton Southwest Atlanta Christian (GA) Washington Wizards Samuel Dalembert St. Patrick (NJ) New York Knicks Guillermo Diaz Miami Christian (FL) Los Angeles Clippers Juan Dixon Calvert Hall (MD) Washington Wizards Kevin Durant Fort Washington (MD) Oklahoma City Thunder Daniel Ewing Willowridge (TX) Los Angeles Clippers Anthony Farmer Artesia (CA) Golden State Warriors Raymond Felton Latta (SC) Dallas Mavericks Joe Forte DeMatha (MD) Seattle SuperSonics T.J. Ford Willowridge (TX) San Antonio Spurs Rudy Gay Archbishop Spalding (MD) Sacramento Kings Eddie Griffin Roman Catholic (PA) Minnesota Timberwolves Al Harrington St. Patrick (NJ) Washington Wizards 99 Kings Highway Dover, DE 19901 (302) 672-6832 (302) 739-5749 fax www.SlamDunkToTheBeach.com @SlamDunkToBeach Slam Dunk to the Beach Notable NBA Alumni Roy Hibbert Georgetown Prep (MD) Indiana Pacers Dwight Howard Southwest Atlanta Christian (GA) Houston Rockets Kris Humphries Hopkins (MN) Washington Wizards LeBron James St. Vincent-St. Mary (OH) Cleveland Cavaliers Kyle Lowry Cardinal Dougherty (PA) Toronto Raptors Pops Mensah-Bonsu St. -

National Basketball Association Official
NATIONAL BASKETBALL ASSOCIATION OFFICIAL SCORER'S REPORT FINAL BOX 3/16/2011 ORACLE Arena, Oakland, CA Officials: #10 Ron Garretson, #52 Pat Fraher, #63 Derek Richardson Time of Game: 2:20 Attendance: 19,596 (Sellout) VISITOR: Dallas Mavericks (48-20) NO PLAYER MIN FG FGA 3P 3PA FT FTA OR DR TOT A PF ST TO BS PTS 41 Dirk Nowitzki F 34:39 10 22 2 3 12 12 6 7 13 2 3 0 1 1 34 13 Corey Brewer F 5:41 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 6 Tyson Chandler C 37:40 5 6 0 0 3 4 2 7 9 1 3 2 1 0 13 3 Rodrigue Beaubois G 37:03 7 11 1 4 3 3 0 2 2 4 2 4 1 0 18 2 Jason Kidd G 34:06 1 6 1 6 1 2 1 4 5 11 2 0 4 0 4 0 Shawn Marion 27:37 6 10 0 0 2 2 0 4 4 2 3 0 1 0 14 31 Jason Terry 38:27 7 12 3 4 2 2 1 5 6 6 0 0 2 0 19 11 JJ Barea 14:35 4 8 1 2 1 2 0 2 2 2 1 0 2 0 10 28 Ian Mahinmi 3:12 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 35 Brian Cardinal 7:00 0 0 0 0 0 0 0 0 0 0 1 0 2 0 0 33 Brendan Haywood DND- Lower Back Stiffness 92 DeShawn Stevenson DNP - Coach's Decision TOTALS: 40 77 8 19 24 27 10 31 41 28 16 6 14 1 112 PERCENTAGES: 51.9% 42.1% 88.9% TM REB: 5 TOT TO: 14 (21 PTS) HOME: GOLDEN STATE WARRIORS (30-38) NO PLAYER MIN FG FGA 3P 3PA FT FTA OR DR TOT A PF ST TO BS PTS 1 Dorell Wright F 40:24 5 13 4 8 0 0 0 1 1 1 3 2 0 0 14 10 David Lee F 39:05 10 14 0 0 2 2 1 8 9 1 2 3 2 0 22 15 Andris Biedrins C 22:06 3 5 0 0 1 2 3 5 8 0 1 1 2 0 7 8 Monta Ellis G 43:48 10 20 2 8 4 4 1 5 6 11 2 2 5 1 26 30 Stephen Curry G 32:14 4 10 2 4 0 1 0 0 0 5 2 1 3 0 10 2 Acie Law 22:44 5 7 0 1 5 6 0 2 2 6 4 2 1 0 15 20 Ekpe Udoh 19:27 2 6 0 0 1 4 1 0 1 0 3 0 0 2 5 23 Al Thornton 8:08 1 3 0 0 0 -

Vs. Cal State Monterey.Pmd
FRESNO STATE A T H L E T I C S M E D I A R E L A T I O N S www.gobulldogs.com 5305 N. Campus Dr. • Rm 153 • Fresno, CA 93740-8020 • 559-278-2509 • Fax: 559-278-4689 Exhibition 2 EXH Final 2003-04 WAC Standings Fresno State Closes Out – WAC –– Overall – W L Pct. W L Pct. Exhibition Schedule With ––––––––––––––––––––––––––––––––––––––––––––––––––––––––– 2 Nevada 13 5 .722 25 9 .735 ––––––––––––––––––––––––––––––––––––––––––––––––––––––––– CSU Monterey Bay UTEP 13 5 .722 24 8 .750 Fresno State ––––––––––––––––––––––––––––––––––––––––––––––––––––––––– Fresh off an easy win in its first exhibition Boise State 12 6 .667 23 10 .697 vs. ––––––––––––––––––––––––––––––––––––––––––––––––––––––––– on Monday, Fresno State takes the court Rice 12 6 .667 22 11 .667 this afternoon against CSU Monterey Bay ––––––––––––––––––––––––––––––––––––––––––––––––––––––––– CSU Monterey Bay Hawaii 11 7 .611 21 12 .636 for its second of two preseason games. ––––––––––––––––––––––––––––––––––––––––––––––––––––––––– Fresno State 10 8 .556 14 15 .483 Game Facts The Bulldogs opened up the exhibition ––––––––––––––––––––––––––––––––––––––––––––––––––––––––– Sunday, Nov. 14 • 3 p.m. Louisiana Tech 8 10 .444 15 15 .500 season with an 81-63 victory over Fresno ––––––––––––––––––––––––––––––––––––––––––––––––––––––––– –––––––––––––––––––––––––––––––––––––––––––––––––––––––– SMU 5 13 .278 12 19 .400 Fresno, Calif. • Save Mart Center (16,116) Pacific, with Donovan Morris getting his ––––––––––––––––––––––––––––––––––––––––––––––––––––––––– –––––––––––––––––––––––––––––––––––––––––––––––––––––––– -

Media Information 2015
2015 SLAM DUNK TO THE BEACH PRESENTED BY THE DELAWARE SPORTS COMMISSION CAPE HENLOPEN HIGH SCHOOL – LEWES, DE Scott Klatzkin, Media Coordinator | Cell: 302-530-4492 | [email protected] Marc Steigwerwalt, Position Sports | [email protected] slamdunktothebeach.com | Twiiter @slamdunktobeach | #SlamDunkDE | Instagram @SlamDunkDE MEDIA INFORMATION: DECEMBER 27 - 29 SLAM DUNK TEAMS AMONGST NATION’S BEST: The 2015 field is headlined by five schools SCHEDULE ranked in the MaxPreps Xcellent 25. Seventh ranked The Patrick School, 11th ranked La Lumiere, 13th ranked Roselle Catholic, 19th ranked Neumann-Goretti and 20th ranked Roman December 27 Day Session Catholic were all listed in the most recent rankings released on December 24th, with St. 12:00pm Maret School (DC) vs. Benedict’s amongst the teams “knocking on the door.” Appoquinimink (DE) In addition to the current MaxPreps rankings, nine of the 13 teams from the national field were 1:30pm Bishop O’Connell (VA) vs. listed as MaxPreps “Early Contenders” for the 2015-16 season. La Lumiere, Roman Catholic, Mount Pleasant (DE) Roselle Catholic, Ss. Neumann-Goretti and The Patrick School were all ranked in the Top 25, 3:00pm Friendship Collegiate (DC) vs. while Bishop McNamara, Paul VI, St. Benedict’s Prep, and Westtown School all made the St. Raymond (NY) MaxPreps rankings as teams “On the Radar.” December 27 Night Session 6:00pm Cape Henlopen (DE) vs. SLAM DUNK GAMES TO BE SEEN ANYWHERE: For Bishop McNamara (MD) the second season in a row, fans can also watch all the exciting Slam Dunk to the Beach action both online 7:30pm Ss. -

Extras for the Ukiah Daily Journal
UHS girls REMINISCE basketball SUNDAY Elusive Images photo contest ..........Page A-8 Jan. 22, 2006 ................................Page A-3 INSIDE Mendocino County’s World briefly The Ukiah local newspaper .......Page A-2 Monday: A full day of sunshine Tuesday: Mostly sunny $1 tax included DAILY JOURNAL ukiahdailyjournal.com 54 pages, Volume 147 Number 288 email: [email protected] Solar-powered home incentives funded By BEN BROWN capacity in California by 3,000 was announced earlier this month. but it also represents the collusion incentive payment per watt of elec- The Daily Journal megawatts a year by 2017. “Now it’s up to Californians to make years of political uncertainty in many tricity produced by an individual The California Public Utilities “Today’s decision signals Califo- this a reality by stepping up to the oil producing countries and a desire photovoltaic array. Individuals and Commission will be funding the rnia’s vote for a cleaner, more reli- plate to go solar.” for energy independence, said Adam businesses receiving electricity or California Solar Initiative, an 11- able energy future,” said Rachelle This victory for clean energy Browning, director of operations for gas from investor-owned utility com- year, $3.2 billion incentive program Chong, California Public Utilities advocates was the result of three the Vote Solar Initiative. aimed at increasing the solar energy Commissioner, when the decision years of hard work by many people, The program will provide a $2.80 See SOLAR, Page A-14 THOMPSON SWEET SATURDAYS AT THE UKIAH LIBRARY ON COAST: Queries Children’s toys crowned fielded, By BEN BROWN The Daily Journal even if ayla Meadows, a River Oak Charter School unpopular kindergarten teacher, stands at By FRANK HARTZELL the door to the Fort Bragg Advocate-News Kchildren’s room of the Mendocino When Mike Thompson’s County Library Saturday morning, mom first brought him to the greeting children and parents as Little River Inn, it was to they enter for the first Sweet soothe the allergies of the Saturday event of the year. -

Top Players for the 2000 NBA Draft (Note: As of June 16Th
Roundball Review’s Top Players for the 2000 NBA Draft (Note: As of June 16th. The NBA Draft will be held on June 28 at Target Center in Minneapolis, MN.) Players are seniors unless noted otherwise. FORWARDS : Grade: B. GUARDS : GRADE: B. TIER ONE : 1. Kenyon Martin 6-9 230 Cincinnati TIER ONE : 2. Stromile Swift—soph 6-9 225 LSU 1. Courtney Alexander 6-5 200 Fresno State 3. Marcus Fizer—junior 6-7 260 Iowa State 2. Quentin Richardson—sophomore 4. Darius Miles—HS 6’9 221 East St. Louis 6-6 225 DePaul 5. Mike Miller—soph. 6-8 220 Florida 3. DerMarr Johnson—freshman 6. Morris Peterson 6-6 215 Michigan State 6-9 200 Cincinnati 7. Jerome Moiso—soph. 6-10 230 UCLA 4. Erick Barkley—soph. 6-2 185 St. John’s 8. Etan Thomas 6-9 247 Syracuse 5. Mateen Cleaves 6-2 195 Michigan State 9. Olumide Oyedeji—196-11 240 Nigeria 6. Michael Redd—jr. 6-6 205 Ohio State 10. Desmond Mason 6-5.25 207 Oklahoma State 7. Keyon Dooling—sophomore 6-3 184 Missouri 8. Scoonie Penn 5-9 178 Ohio State TIER TWO : 9. Chris Carrawell 6-6 215 Duke 11. Donnell Harvey—frosh. 10. DeShawn Stevenson—high school senior 6-8 216 Florida 6-6 200 Wash. Union (CA) 12. Hanno Möttölä 6-10 240 Utah 13. Chris Porter 6-5 216 Auburn 14. Pete Mickeal 6-4.75 220 Cincinnati TIER TWO : 15. Jason Collier 7-0 250 Georgia Tech 11. Craig “Speedy” Claxton 16. -

Mason – Complaint
EFiled: Apr 09 2018 01:50PM EDT Transaction ID 61891536 Case No. 2018-0263- IN THE COURT OF CHANCERY OF THE STATE OF DELAWARE ROGER MASON, ) ) Plaintiff, ) ) v. ) C.A. No. 2018-____-___ ) BIG3 BASKETBALL, LLC, ) ) Defendant. ) VERIFIED COMPLAINT FOR INSPECTION OF BOOKS AND RECORDS Plaintiff, Roger Mason (“Mason”), by and through his undersigned counsel, alleges his Verified Complaint for Inspection of Books and Records against defendant BIG3 Basketball, LLC (the “Company” or “BIG3”) as follows: Nature of the Action 1. This is an action under 6 Del. C. § 18-305 (“Section 18-305”) to compel the Company to provide Mason certain books and records. 2. On March 21, 2018, Mason, a member of the Company, delivered a written demand (the “Demand”) to the Company seeking to inspect certain books and records of the Company. Indeed, the Company did not even respond to Mason’s Demand. A true and correct copy of the Demand is attached hereto as Exhibit 1. RLF1 19114768v.1 3. The Company has failed to comply with its obligations and has refused to allow Mason to inspect the requested books and records. Mason therefore requires this Court’s assistance. The Parties 4. Mason, a New Jersey resident, has been a member of the Company at all relevant times. 5. The Company is a limited liability company organized under the laws of the State of Delaware, with its principal place of business in California. The Company operates a 3-on-3 basketball league, BIG3 Basketball (the “League”), from June through August, featuring numerous retired National Basketball Association (“NBA”) players.