DOCSLIB.ORG

Topics in Cosmology: Island Universes, Cosmological Perturbations and Dark Energy

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Topics in Cosmology: Island Universes, Cosmological Perturbations and Dark Energy TOPICS IN COSMOLOGY: ISLAND UNIVERSES, COSMOLOGICAL PERTURBATIONS AND DARK ENERGY by SOURISH DUTTA Submitted in partial fulfillment of the requirements for the degree Doctor of Philosophy Department of Physics CASE WESTERN RESERVE UNIVERSITY August 2007 CASE WESTERN RESERVE UNIVERSITY SCHOOL OF GRADUATE STUDIES We hereby approve the dissertation of ______________________________________________________ candidate for the Ph.D. degree *. (signed)_______________________________________________ (chair of the committee) ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ (date) _______________________ *We also certify that written approval has been obtained for any proprietary material contained therein. To the people who have believed in me. Contents Dedication iv List of Tables viii List of Figures ix Abstract xiv 1 The Standard Cosmology 1 1.1 Observational Motivations for the Hot Big Bang Model . 1 1.1.1 Homogeneity and Isotropy . 1 1.1.2 Cosmic Expansion . 2 1.1.3 Cosmic Microwave Background . 3 1.2 The Robertson-Walker Metric and Comoving Co-ordinates . 6 1.3 Distance Measures in an FRW Universe . 11 1.3.1 Proper Distance . 12 1.3.2 Luminosity Distance . 14 1.3.3 Angular Diameter Distance . 16 1.4 The Friedmann Equation . 18 1.5 Model Universes . 21 1.5.1 An Empty Universe . 22 1.5.2 Generalized Flat One-Component Models . 22 1.5.3 A Cosmological Constant Dominated Universe . 24 1.5.4 de Sitter space . 26 1.5.5 Flat Matter Dominated Universe . 27 1.5.6 Curved Matter Dominated Universe . 28 1.5.7 Flat Radiation Dominated Universe . 30 1.5.8 Matter Radiation Equality . 32 1.6 Gravitational Lensing . 34 1.7 The Composition of the Universe . 39 v 1.7.1 Measuring the Total Matter Content . 39 1.7.2 Ordinary and Dark Matter . 42 1.7.3 Supernovae and Cosmic Acceleration . 45 1.7.4 Cosmic Microwave Background Anisotropies . 49 1.8 Shortcomings of the Standard Cosmology . 58 1.8.1 The Flatness Problem . 58 1.8.2 The Entropy Problem . 59 1.8.3 The Horizon Problem . 59 1.8.4 The Monopole Problem . 60 1.9 Inflation . 62 1.9.1 Inflation and the Problems of the Standard Cosmology . 62 1.9.2 The Dynamics of Inflation . 64 1.9.3 The Slow Roll Parameters . 66 1.9.4 Models of Inflation . 67 1.9.5 Issues with Inflation . 69 2 Island Cosmology 76 2.1 Introduction . 76 2.2 The Model . 77 2.3 NEC violations in de Sitter space . 80 2.4 Extent and duration of NEC violation . 82 2.5 Likelihood – the role of the observer . 87 2.6 The NEC violating field . 89 2.7 Assumptions . 91 2.8 Conclusions . 94 3 Perturbation Spectra 98 3.1 Introduction . 98 3.2 The Theory of Cosmological Perturbations . 98 3.2.1 The metric perturbations . 99 3.2.2 Gauge Issues in Cosmology . 101 3.2.3 The Comoving Curvature Perturbation . 103 3.2.4 The Power Spectrum . 104 3.2.5 The Equations of Motion . 106 3.2.6 Quantum Theory of Cosmological Perturbations . 108 3.3 Difficulties in computing perturbations from Island Cosmology . 112 3.3.1 Classical vs Quantum Fields . 112 3.3.2 Backreaction on spacetime . 113 3.4 Perturbations in a Spectator Field . 117 3.5 A Classical Treatment of Island Cosmology . 120 vi 3.5.1 Introduction . 120 3.5.2 The de Sitter phase . 121 3.5.3 The Phantom Phase . 122 3.5.4 The Radiation Dominated FRW Phase . 125 3.5.5 Calculational Strategy . 125 3.6 Spectrum from a Classical Treatment . 127 3.6.1 vk in the de Sitter and FRW phases . 127 3.6.2 vk in the Phantom Phase . 128 3.6.3 Calculation of Unknown Constants . 135 3.6.4 Determination of the Scalar Power Spectrum . 138 3.6.5 Determination of the Tensor Power Spectrum . 138 3.7 Conclusion . 140 4 Dark Energy Voids 144 4.1 Introduction . 144 4.2 What is causing the acceleration? . 145 4.3 The model . 147 4.3.1 Linearization . 150 4.3.2 Potential . 153 4.3.3 Initial conditions . 153 4.4 Results . 155 4.4.1 Density contrasts . 155 4.4.2 Equation of state . 160 4.5 Discussion . 163 4.5.1 Void formation . 163 4.5.2 Generality . 165 4.6 Conclusions . 166 Bibliography 172 vii List of Tables 3.1 Scalar-Vector-Tensor decomposition of metric perturbations . 100 viii List of Figures 1.1 The spectrum of the CMB, as seen by COBE. http://lambda.gsfc. nasa.gov/product/cobe/firas_image.cfm .............. 4 1.2 Gravitational lensing geometry. The lens distorts the ”true” angles β (that would have been seen without any lensing effects) into the angles θ. Source [15] . 34 1.3 A flow chart showing the classifications of Supernovae http://rsd-www. nrl.navy.mil/7212/montes/snetax.html. 46 1.4 top panel: A Hubble diagram made from data from both the Supernova Cosmology Project and the High-z Supernova Search Team taken from [13].bottom panel The residual of the distances relative to a ΩM = 0.3, ΩΛ = 0.7 Universe. 50 1.5 Best fit regions in the (ΩM ,ΩΛ) plane for data from both the Super- nova Cosmology Project and the High-z Supernova Search Team. The agreement of the two experiments is remarkable. Source [13] . 51 1.6 The Dipole Anisotropy in the CMB as seen by COBE http://map. gsfc.nasa.gov/m_uni/uni_101Flucts.html. 52 1.7 The CMB spectrum once the dipole is subtracted. http://map.gsfc. nasa.gov/m_uni/uni_101Flucts.html. 53 1.8 The WMAP three-year power spectrum (in black) together with data from other recent experiments measuring the CMB angular power spec- trum. Taken from [44] . 56 1.9 A plot of length scale vs (logarithmic) scale factor in an FRW cosmol- ogy. The blue line shows the evolution of the Hubble scale. The red lines show the evolution of physical scales. Since the Hubble length evolves faster than the physical scales, sub-Horizon modes have never been in causal contact prior to Horizon entry. 61 1.10 Physical scales entering the horizon at the time of last scattering have been in causal contact before. 63 ix 2.1 Sketch of the behavior of the Hubble length scale with conformal time, η, in the Island model, and the evolution of fluctuation modes. At early times, inflation is driven by the presently observed dark energy, assumed to be a cosmological constant. As the cosmological constant is very small, the Hubble length scale is very large – of order the present horizon size. Exponential inflation in some horizon volume ends not due to the decay of the vacuum energy as in inflationary scenarios but due to a quantum fluctuation in the time interval (ηi, ηf ) that violates the null energy condition (NEC). The NEC violating quantum fluctu- ation causes the Hubble length scale to decrease. After the fluctuation is over, the universe enters radiation dominated FRW expansion, and the Hubble length scale grows with time. The physical wavelength of a −1 quantum fluctuation mode starts out less than HΛ at some early time ηi. The mode exits the cosmological horizon during the NEC violating fluctuation (ηexit) and then re-enters the horizon at some later epoch (ηentry) during the FRW epoch (The modes are drawn as straight lines for illustrative purposes only, they actually grow in proportion to the scale factor). 78 2.2 We show a classical de Sitter spacetime for conformal time η < ηP , that transitions to a faster expanding classical de Sitter spacetime for η > ηQ. The inverse Hubble size is shown by the white region. A bundle of ingoing null rays originating at point a is convergent initially but becomes divergent in the superhorizon region at point b. This can only occur if the NEC is violated in the region η ∈ (ηP , ηQ). In the quantum domain, a classical picture of spacetime may not be valid and this is made explicit by the question marks. 83 2.3 A spacetime diagram similar to that in Fig. 2.2 but one in which the NEC violation occurs over a sub-horizon region (shaded region in the diagram). Now the null ray bundle from a to b goes from being converg- ing (within the horizon) to diverging (outside the horizon). However, it does not encounter any NEC violation along its path, and this is not possible as can be seen from the Raychaudhuri equation. Since the ingoing null rays are convergent as far out as the point P , the size of the quantum domain has to extend out to at least the inverse Hubble size of the initial de Sitter space. Therefore the NEC violating patch has to extend beyond the initial horizon. 85 x 4.1 The evolution of the DDE overdensity δφ at the center of the matter perturbation, r = 0, with redshift (1+z).The scale of the perturbation is σHi = 0.01, and the mass is m/H0 = 1. Initially homogenous, the DDE develops an underdensity at late times in response to the matter perturbation. 156 4.2 Same as Figure 4.1, with the y-axis on a logarithmic scale. The DDE tends to cluster initially, but eventually forms a void. The kink in the plot signifies the change-over from positive to negative perturbation. 156 4.3 Logarithmic profiles of the matter density contrast log10 |δm| and the dark energy density contrast log10 |δφ|, at three different redshifts. Solid lines denote the DDE profiles, and dotted lines denote the matter profiles.158 4.4 DDE density contrast δφ at the center of the matter perturbation r = 0 as a function of the redshift (1 + z) for fixed mass m/H0 = 1 and different initial matter perturbations’ widths.
Load more

Recommended publications
  • Birth of De Sitter Universe from a Time Crystal Universe
    PHYSICAL REVIEW D 100, 123531 (2019) Birth of de Sitter universe from a time crystal universe † Daisuke Yoshida * and Jiro Soda Department of Physics, Kobe University, Kobe 657-8501, Japan (Received 30 September 2019; published 18 December 2019) We show that a simple subclass of Horndeski theory can describe a time crystal universe. The time crystal universe can be regarded as a baby universe nucleated from a flat space, which is mediated by an extension of Giddings-Strominger instanton in a 2-form theory dual to the Horndeski theory. Remarkably, when a cosmological constant is included, de Sitter universe can be created by tunneling from the time crystal universe. It gives rise to a past completion of an inflationary universe. DOI: 10.1103/PhysRevD.100.123531 I. INTRODUCTION Euler-Lagrange equations of motion contain up to second order derivatives. Actually, bouncing cosmology in the Inflation has succeeded in explaining current observa- Horndeski theory has been intensively investigated so far tions of the large scale structure of the Universe [1,2]. [23–29]. These analyses show the presence of gradient However, inflation has a past boundary [3], which could be instability [30,31] and finally no-go theorem for stable a true initial singularity or just a coordinate singularity bouncing cosmology in Horndeski theory was found for the depending on how much the Universe deviates from the spatially flat universe [32]. However, it was shown that the exact de Sitter [4], or depending on the topology of the no-go theorem does not hold when the spatial curvature is Universe [5].
    [Show full text]
  • Expanding Space, Quasars and St. Augustine's Fireworks
    Universe 2015, 1, 307-356; doi:10.3390/universe1030307 OPEN ACCESS universe ISSN 2218-1997 www.mdpi.com/journal/universe Article Expanding Space, Quasars and St. Augustine’s Fireworks Olga I. Chashchina 1;2 and Zurab K. Silagadze 2;3;* 1 École Polytechnique, 91128 Palaiseau, France; E-Mail: [email protected] 2 Department of physics, Novosibirsk State University, Novosibirsk 630 090, Russia 3 Budker Institute of Nuclear Physics SB RAS and Novosibirsk State University, Novosibirsk 630 090, Russia * Author to whom correspondence should be addressed; E-Mail: [email protected]. Academic Editors: Lorenzo Iorio and Elias C. Vagenas Received: 5 May 2015 / Accepted: 14 September 2015 / Published: 1 October 2015 Abstract: An attempt is made to explain time non-dilation allegedly observed in quasar light curves. The explanation is based on the assumption that quasar black holes are, in some sense, foreign for our Friedmann-Robertson-Walker universe and do not participate in the Hubble flow. Although at first sight such a weird explanation requires unreasonably fine-tuned Big Bang initial conditions, we find a natural justification for it using the Milne cosmological model as an inspiration. Keywords: quasar light curves; expanding space; Milne cosmological model; Hubble flow; St. Augustine’s objects PACS classifications: 98.80.-k, 98.54.-h You’d think capricious Hebe, feeding the eagle of Zeus, had raised a thunder-foaming goblet, unable to restrain her mirth, and tipped it on the earth. F.I.Tyutchev. A Spring Storm, 1828. Translated by F.Jude [1]. 1. Introduction “Quasar light curves do not show the effects of time dilation”—this result of the paper [2] seems incredible.
    [Show full text]
  • Lecture 8: the Big Bang and Early Universe
    Astr 323: Extragalactic Astronomy and Cosmology Spring Quarter 2014, University of Washington, Zeljkoˇ Ivezi´c Lecture 8: The Big Bang and Early Universe 1 Observational Cosmology Key observations that support the Big Bang Theory • Expansion: the Hubble law • Cosmic Microwave Background • The light element abundance • Recent advances: baryon oscillations, integrated Sachs-Wolfe effect, etc. 2 Expansion of the Universe • Discovered as a linear law (v = HD) by Hubble in 1929. • With distant SNe, today we can measure the deviations from linearity in the Hubble law due to cosmological effects • The curves in the top panel show a closed Universe (Ω = 2) in red, the crit- ical density Universe (Ω = 1) in black, the empty Universe (Ω = 0) in green, the steady state model in blue, and the WMAP based concordance model with Ωm = 0:27 and ΩΛ = 0:73 in purple. • The data imply an accelerating Universe at low to moderate redshifts but a de- celerating Universe at higher redshifts, consistent with a model having both a cosmological constant and a significant amount of dark matter. 3 Cosmic Microwave Background (CMB) • The CMB was discovered by Penzias & Wil- son in 1965 (although there was an older mea- surement of the \sky" temperature by McKel- lar using interstellar molecules in 1940, whose significance was not recognized) • This is the best black-body spectrum ever mea- sured, with T = 2:73 K. It is also remark- ably uniform accross the sky (to one part in ∼ 10−5), after dipole induced by the solar mo- tion is corrected for. • The existance of CMB was predicted by Gamow in 1946.
    [Show full text]
  • Arxiv:1803.02804V1 [Hep-Ph] 7 Mar 2018 It Must Have Some Rather Specific Characteristics
    FERMILAB-PUB-18-066-A Severely Constraining Dark Matter Interpretations of the 21-cm Anomaly Asher Berlina,∗ Dan Hooperb;c;d,y Gordan Krnjaicb,z and Samuel D. McDermottbx aSLAC National Accelerator Laboratory, Menlo Park CA, 94025, USA bFermi National Accelerator Laboratory, Theoretical Astrophysics Group, Batavia, IL, USA cUniversity of Chicago, Kavli Institute for Cosmological Physics, Chicago IL, USA and dUniversity of Chicago, Department of Astronomy and Astrophysics, Chicago IL, USA (Dated: March 8, 2018) The EDGES Collaboration has recently reported the detection of a stronger-than-expected ab- sorption feature in the global 21-cm spectrum, centered at a frequency corresponding to a redshift of z ∼ 17. This observation has been interpreted as evidence that the gas was cooled during this era as a result of scattering with dark matter. In this study, we explore this possibility, applying constraints from the cosmic microwave background, light element abundances, Supernova 1987A, and a variety of laboratory experiments. After taking these constraints into account, we find that the vast majority of the parameter space capable of generating the observed 21-cm signal is ruled out. The only range of models that remains viable is that in which a small fraction, ∼ 0:3 − 2%, of the dark matter consists of particles with a mass of ∼ 10 − 80 MeV and which couple to the photon through a small electric charge, ∼ 10−6 −10−4. Furthermore, in order to avoid being overproduced in the early universe, such models must be supplemented with an additional depletion mechanism, such as annihilations through a Lµ − Lτ gauge boson or annihilations to a pair of rapidly decaying hidden sector scalars.
    [Show full text]
  • Report from the Dark Energy Task Force (DETF)
    Fermi National Accelerator Laboratory Fermilab Particle Astrophysics Center P.O.Box 500 - MS209 Batavia, Il l i noi s • 60510 June 6, 2006 Dr. Garth Illingworth Chair, Astronomy and Astrophysics Advisory Committee Dr. Mel Shochet Chair, High Energy Physics Advisory Panel Dear Garth, Dear Mel, I am pleased to transmit to you the report of the Dark Energy Task Force. The report is a comprehensive study of the dark energy issue, perhaps the most compelling of all outstanding problems in physical science. In the Report, we outline the crucial need for a vigorous program to explore dark energy as fully as possible since it challenges our understanding of fundamental physical laws and the nature of the cosmos. We recommend that program elements include 1. Prompt critical evaluation of the benefits, costs, and risks of proposed long-term projects. 2. Commitment to a program combining observational techniques from one or more of these projects that will lead to a dramatic improvement in our understanding of dark energy. (A quantitative measure for that improvement is presented in the report.) 3. Immediately expanded support for long-term projects judged to be the most promising components of the long-term program. 4. Expanded support for ancillary measurements required for the long-term program and for projects that will improve our understanding and reduction of the dominant systematic measurement errors. 5. An immediate start for nearer term projects designed to advance our knowledge of dark energy and to develop the observational and analytical techniques that will be needed for the long-term program. Sincerely yours, on behalf of the Dark Energy Task Force, Edward Kolb Director, Particle Astrophysics Center Fermi National Accelerator Laboratory Professor of Astronomy and Astrophysics The University of Chicago REPORT OF THE DARK ENERGY TASK FORCE Dark energy appears to be the dominant component of the physical Universe, yet there is no persuasive theoretical explanation for its existence or magnitude.
    [Show full text]
  • The State of the Multiverse: the String Landscape, the Cosmological Constant, and the Arrow of Time
    The State of the Multiverse: The String Landscape, the Cosmological Constant, and the Arrow of Time Raphael Bousso Center for Theoretical Physics University of California, Berkeley Stephen Hawking: 70th Birthday Conference Cambridge, 6 January 2011 RB & Polchinski, hep-th/0004134; RB, arXiv:1112.3341 The Cosmological Constant Problem The Landscape of String Theory Cosmology: Eternal inflation and the Multiverse The Observed Arrow of Time The Arrow of Time in Monovacuous Theories A Landscape with Two Vacua A Landscape with Four Vacua The String Landscape Magnitude of contributions to the vacuum energy graviton (a) (b) I Vacuum fluctuations: SUSY cutoff: ! 10−64; Planck scale cutoff: ! 1 I Effective potentials for scalars: Electroweak symmetry breaking lowers Λ by approximately (200 GeV)4 ≈ 10−67. The cosmological constant problem −121 I Each known contribution is much larger than 10 (the observational upper bound on jΛj known for decades) I Different contributions can cancel against each other or against ΛEinstein. I But why would they do so to a precision better than 10−121? Why is the vacuum energy so small? 6= 0 Why is the energy of the vacuum so small, and why is it comparable to the matter density in the present era? Recent observations Supernovae/CMB/ Large Scale Structure: Λ ≈ 0:4 × 10−121 Recent observations Supernovae/CMB/ Large Scale Structure: Λ ≈ 0:4 × 10−121 6= 0 Why is the energy of the vacuum so small, and why is it comparable to the matter density in the present era? The Cosmological Constant Problem The Landscape of String Theory Cosmology: Eternal inflation and the Multiverse The Observed Arrow of Time The Arrow of Time in Monovacuous Theories A Landscape with Two Vacua A Landscape with Four Vacua The String Landscape Many ways to make empty space Topology and combinatorics RB & Polchinski (2000) I A six-dimensional manifold contains hundreds of topological cycles.
    [Show full text]
  • Time-Dependent Cosmological Interpretation of Quantum Mechanics Emmanuel Moulay
    Time-dependent cosmological interpretation of quantum mechanics Emmanuel Moulay To cite this version: Emmanuel Moulay. Time-dependent cosmological interpretation of quantum mechanics. 2016. hal- 01169099v2 HAL Id: hal-01169099 https://hal.archives-ouvertes.fr/hal-01169099v2 Preprint submitted on 18 Nov 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Time-dependent cosmological interpretation of quantum mechanics Emmanuel Moulay∗ Abstract The aim of this article is to define a time-dependent cosmological inter- pretation of quantum mechanics in the context of an infinite open FLRW universe. A time-dependent quantum state is defined for observers in sim- ilar observable universes by using the particle horizon. Then, we prove that the wave function collapse of this quantum state is avoided. 1 Introduction A new interpretation of quantum mechanics, called the cosmological interpre- tation of quantum mechanics, has been developed in order to take into account the new paradigm of eternal inflation [1, 2, 3]. Eternal inflation can lead to a collection of infinite open Friedmann-Lemaˆıtre-Robertson-Walker (FLRW) bub- ble universes belonging to a multiverse [4, 5, 6]. This inflationary scenario is called open inflation [7, 8].
    [Show full text]
  • Primordial Gravitational Waves and Cosmology Arxiv:1004.2504V1
    Primordial Gravitational Waves and Cosmology Lawrence Krauss,1∗ Scott Dodelson,2;3;4 Stephan Meyer 3;4;5;6 1School of Earth and Space Exploration and Department of Physics, Arizona State University, PO Box 871404, Tempe, AZ 85287 2Center for Particle Astrophysics, Fermi National Laboratory PO Box 500, Batavia, IL 60510 3Department of Astronomy and Astrophysics 4Kavli Institute of Cosmological Physics 5Department of Physics 6Enrico Fermi Institute University of Chicago, 5640 S. Ellis Ave, Chicago, IL 60637 ∗To whom correspondence should be addressed; E-mail: [email protected]. The observation of primordial gravitational waves could provide a new and unique window on the earliest moments in the history of the universe, and on possible new physics at energies many orders of magnitude beyond those acces- sible at particle accelerators. Such waves might be detectable soon in current or planned satellite experiments that will probe for characteristic imprints in arXiv:1004.2504v1 [astro-ph.CO] 14 Apr 2010 the polarization of the cosmic microwave background (CMB), or later with di- rect space-based interferometers. A positive detection could provide definitive evidence for Inflation in the early universe, and would constrain new physics from the Grand Unification scale to the Planck scale. 1 Introduction Observations made over the past decade have led to a standard model of cosmology: a flat universe dominated by unknown forms of dark energy and dark matter. However, while all available cosmological data are consistent with this model, the origin of neither the dark energy nor the dark matter is known. The resolution of these mysteries may require us to probe back to the earliest moments of the big bang expansion, but before a period of about 380,000 years, the universe was both hot and opaque to electromagnetic radiation.
    [Show full text]
  • Arxiv:Hep-Ph/9912247V1 6 Dec 1999 MGNTV COSMOLOGY IMAGINATIVE Abstract
    IMAGINATIVE COSMOLOGY ROBERT H. BRANDENBERGER Physics Department, Brown University Providence, RI, 02912, USA AND JOAO˜ MAGUEIJO Theoretical Physics, The Blackett Laboratory, Imperial College Prince Consort Road, London SW7 2BZ, UK Abstract. We review1 a few off-the-beaten-track ideas in cosmology. They solve a variety of fundamental problems; also they are fun. We start with a description of non-singular dilaton cosmology. In these scenarios gravity is modified so that the Universe does not have a singular birth. We then present a variety of ideas mixing string theory and cosmology. These solve the cosmological problems usually solved by inflation, and furthermore shed light upon the issue of the number of dimensions of our Universe. We finally review several aspects of the varying speed of light theory. We show how the horizon, flatness, and cosmological constant problems may be solved in this scenario. We finally present a possible experimental test for a realization of this theory: a test in which the Supernovae results are to be combined with recent evidence for redshift dependence in the fine structure constant. arXiv:hep-ph/9912247v1 6 Dec 1999 1. Introduction In spite of their unprecedented success at providing causal theories for the origin of structure, our current models of the very early Universe, in partic- ular models of inflation and cosmic defect theories, leave several important issues unresolved and face crucial problems (see [1] for a more detailed dis- cussion). The purpose of this chapter is to present some imaginative and 1Brown preprint BROWN-HET-1198, invited lectures at the International School on Cosmology, Kish Island, Iran, Jan.
    [Show full text]
  • The Reionization of Cosmic Hydrogen by the First Galaxies Abstract 1
    David Goodstein’s Cosmology Book The Reionization of Cosmic Hydrogen by the First Galaxies Abraham Loeb Department of Astronomy, Harvard University, 60 Garden St., Cambridge MA, 02138 Abstract Cosmology is by now a mature experimental science. We are privileged to live at a time when the story of genesis (how the Universe started and developed) can be critically explored by direct observations. Looking deep into the Universe through powerful telescopes, we can see images of the Universe when it was younger because of the finite time it takes light to travel to us from distant sources. Existing data sets include an image of the Universe when it was 0.4 million years old (in the form of the cosmic microwave background), as well as images of individual galaxies when the Universe was older than a billion years. But there is a serious challenge: in between these two epochs was a period when the Universe was dark, stars had not yet formed, and the cosmic microwave background no longer traced the distribution of matter. And this is precisely the most interesting period, when the primordial soup evolved into the rich zoo of objects we now see. The observers are moving ahead along several fronts. The first involves the construction of large infrared telescopes on the ground and in space, that will provide us with new photos of the first galaxies. Current plans include ground-based telescopes which are 24-42 meter in diameter, and NASA’s successor to the Hubble Space Telescope, called the James Webb Space Telescope. In addition, several observational groups around the globe are constructing radio arrays that will be capable of mapping the three-dimensional distribution of cosmic hydrogen in the infant Universe.
    [Show full text]
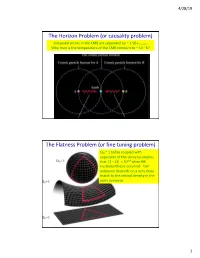
  • Or Causality Problem) the Flatness Problem (Or Fine Tuning Problem
    4/28/19 The Horizon Problem (or causality problem) Antipodal points in the CMB are separated by ~ 1.96 rhorizon. Why then is the temperature of the CMB constant to ~ 10-5 K? The Flatness Problem (or fine tuning problem) W0 ~ 1 today coupled with expansion of the Universe implies that |1 – W| < 10-14 when BB nucleosynthesis occurred. Our existence depends on a very close match to the critical density in the early Universe 1 4/28/19 Theory of Cosmic Inflation Universe undergoes brief period of exponential expansion How Inflation Solves the Flatness Problem 2 4/28/19 Cosmic Inflation Summary Standard Big Bang theory has problems with tuning and causality Inflation (exponential expansion) solves these problems: - Causality solved by observable Universe having grown rapidly from a small region that was in causal contact before inflation - Fine tuning problems solved by the diluting effect of inflation Inflation naturally explains origin of large scale structure: - Early Universe has quantum fluctuations both in space-time itself and in the density of fields in space. Inflation expands these fluctuation in size, moving them out of causal contact with each other. Thus, large scale anisotropies are “frozen in” from which structure can form. Some kind of inflation appears to be required but the exact inflationary model not decided yet… 3 4/28/19 BAO: Baryonic Acoustic Oscillations Predict an overdensity in baryons (traced by galaxies) ~ 150 Mpc at the scale set by the distance that the baryon-photon acoustic wave could have traveled before CMB recombination 4 4/28/19 Curves are different models of Wm A measure of clustering of SDSS Galaxies of clustering A measure Eisenstein et al.
    [Show full text]
  • The Age of the Universe, the Hubble Constant, the Accelerated Expansion and the Hubble Effect
    The age of the universe, the Hubble constant, the accelerated expansion and the Hubble effect Domingos Soares∗ Departamento de F´ısica,ICEx, UFMG | C.P. 702 30123-970, Belo Horizonte | Brazil October 25, 2018 Abstract The idea of an accelerating universe comes almost simultaneously with the determination of Hubble's constant by one of the Hubble Space Tele- scope Key Projects. The age of the universe dilemma is probably the link between these two issues. In an appendix, I claim that \Hubble's law" might yet to be investigated for its ultimate cause, and suggest the \Hubble effect” as the searched candidate. 1 The age dilemma The age of the universe is calculated by two different ways. Firstly, a lower limit is given by the age of the presumably oldest objects in the Milky Way, e.g., globular clusters. Their ages are calculated with the aid of stellar evolu- tion models which yield 14 Gyr and 10% uncertainty. These are fairly confident figures since the basics of stellar evolution are quite solid. Secondly, a cosmo- logical age based on the Standard Cosmology Model derived from the Theory of General Relativity. The three basic models of relativistic cosmology are given by the Friedmann's solutions of Einstein's field equations. The models are char- acterized by a decelerated expansion from a spatial singularity at cosmic time t = 0, and whose magnitude is quantified by the density parameter Ω◦, the present ratio of the mass density in the universe to the so-called critical mass arXiv:0908.1864v8 [physics.gen-ph] 28 Jul 2015 density.
    [Show full text]