DOCSLIB.ORG

Research Article Existence of Solutions to Anti-Periodic Boundary Value Problem for Nonlinear Fractional Differential Equations with Impulses

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Research Article Existence of Solutions to Anti-Periodic Boundary Value Problem for Nonlinear Fractional Differential Equations with Impulses Hindawi Publishing Corporation Advances in Difference Equations Volume 2011, Article ID 915689, 17 pages doi:10.1155/2011/915689 Research Article Existence of Solutions to Anti-Periodic Boundary Value Problem for Nonlinear Fractional Differential Equations with Impulses Anping Chen1, 2 and Yi Chen2 1 Department of Mathematics, Xiangnan University, Chenzhou, Hunan 423000, China 2 School of Mathematics and Computational Science, Xiangtan University, Xiangtan, Hunan 411005, China Correspondence should be addressed to Anping Chen, [email protected] Received 20 October 2010; Revised 25 December 2010; Accepted 20 January 2011 Academic Editor: Dumitru Baleanu Copyright q 2011 A. Chen and Y. Chen. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. This paper discusses the existence of solutions to antiperiodic boundary value problem for nonlinear impulsive fractional differential equations. By using Banach fixed point theorem, Schaefer fixed point theorem, and nonlinear alternative of Leray-Schauder type theorem, some existence results of solutions are obtained. An example is given to illustrate the main result. 1. Introduction In this paper, we consider an antiperiodic boundary value problem for nonlinear fractional differential equations with impulses C α D ut ft, ut,t∈ 0,T,t/ tk,k 1, 2,...,p, Δu| I ut , Δu| J ut ,k , ,...,p, ttk k k ttk k k 1 2 1.1 u0 uT 0,u0 u T 0, C α where T is a positive constant, 1 <α≤ 2, D denotes the Caputo fractional derivative of α f ∈ C ,T × R, R I J R → R {t } t <t <t < ··· <t < order , 0 , k, k : and k satisfy that 0 0 1 2 p t T Δu| ut − ut− Δu| ut − ut− ut ut− p 1 , ttk k k , ttk k k , k and k represent the right and left limits of ut at t tk. Fractional differential equations have proved to be an excellent tool in the mathematic modeling of many systems and processes in various fields of science and engineering. Indeed, we can find numerous applications in viscoelasticity, electrochemistry, control, 2 Advances in Difference Equations electromagnetic, porous media, and so forth. In consequence, the subject of fractional differential equations is gaining much importance and attention see 1–6 and the references therein. The theory of impulsive differential equations has found its extensive applications in realistic mathematic modeling of a wide variety of practical situations and has emerged as an important area of investigation in recent years. For the general theory of impulsive differential equations, we refer the reader to 7, 8. Recently, many authors are devoted to the study of boundary value problems for impulsive differential equations of integer order, see 9–12. Very recently, there are only a few papers about the nonlinear impulsive differential equations and delayed differential equations of fractional order. Agarwal et al. in 13 have established some sufficient conditions for the existence of solutions for a class of initial value problems for impulsive fractional differential equations involving the Caputo farctional derivative. Ahmad et al. in 14 have discussed some existence results for the two-point boundary value problem involving nonlinear impulsive hybrid differential equation of fractional order by means of contraction mapping principle and Krasnoselskii’s fixed point theorem. By the similar way, they have also obtained the existence results for integral boundary value problem of nonlinear impulsive fractional differential equations see 15. Tian et al. in 16 have obtained some existence results for the three-point impulsive boundary value problem involving fractional differential equations by the means of fixed points method. Maraaba et al. in 17, 18 have established the existence and uniqueness theorem for the delay differential equations with Caputo fractional derivatives. Wang et al. in 19 have studied the existence and uniqueness of the mild solution for a class of impulsive fractional differential equations with time-varying generating operators and nonlocal conditions. To the best of our knowledge, few papers exist in the literature devoted to the antiperiodic boundary value problem for fractional differential equations with impulses. This paper studies the existence of solutions of antiperiodic boundary value problem for fractional differential equations with impulses. The organization of this paper is as follows. In Section 2, we recall some definitions of fractional integral and derivative and preliminary results which will be used in this paper. In Section 3, we will consider the existence results for problem 1.1.Wegivethreeresults,the first one is based on Banach fixed theorem, the second one is based on Schaefer fixed point theorem, and the third one is based on the nonlinear alternative of Leray-Schauder type. In Section 4, we will give an example to illustrate the main result. 2. Preliminaries In this section, we present some basic notations, definitions, and preliminary results which will be used throughout this paper. Definition 2.1 see 4. The Caputo fractional derivative of order α of a function f : 0, ∞ → R is defined as t CDαft 1 t − sn−α−1f nsds, n − <α<n,n α , Γn − α 1 1 2.1 0 where α denotes the integer part of the real number α. Advances in Difference Equations 3 Definition 2.2 see 4. The Riemann-Liouville fractional integral of order α>0ofafunction ft, t>0, is defined as t Iαft 1 t − sα−1fsds, Γα 2.2 0 provided that the right side is pointwise defined on 0, ∞. Definition 2.3 see 4. The Riemann-Liouville fractional derivative of order α>0ofa continuous function f : 0, ∞ → R is given by d n t Dαft 1 t − sn−α−1fsds, Γn − α dt 2.3 0 where n α 1andα denotes the integer part of real number α, provided that the right side is pointwise defined on 0, ∞. For the sake of convenience, we introduce the following notation. J ,T,J ,t ,J t ,t ,i , ,...,p− ,J t ,T J J\{t ,t ,...,t } Let 0 0 0 1 i i i 1 1 2 1 p p . 1 2 p . J{u ,T → R | u ∈ CJ,ut ut− ut−ut , ≤ We define PC : 0 k and k exists, and k k 1 k ≤ p}. Obviously, PCJ is a Banach space with the norm u supt∈J |ut|. Definition 2.4. A function u ∈ PCJ is said to be a solution of 1.1 if u satisfies the equation cDαutft, ut t ∈ J Δu| I ut Δu| J ut ,k for , the equations ttk k k , ttk k k 1, 2,...,p, and the condition u0 uT0,u0 u T0. Lemma 2.5 see 20. Let α>0;then IαCDαu t u t c c t c t2 ··· c tn−1, 0 1 2 n−1 2.4 for some ci ∈ R, i 0, 1, 2,...,n− 1, n α 1. Lemma 2.6 nonlinear alternative of Leray-Schauder type 21. Let E be a Banach space with C ⊆ E closed and convex. Assume that U is a relatively open subset of C with 0 ∈ U and A : U → C is continuous, compact map. Then either 1 A has a fixed point in U,or 2 there exists u ∈ ∂U and λ ∈ 0, 1 with u λAu. Lemma 2.7 Schaefer fixed point theorem 22. Let S be a convex subset of a normed linear space Ω and 0 ∈ S.LetF : S → S be a completely continuous operator, and let ζF {u ∈ S : u λFu, for some 0 <λ<1}. 2.5 Then either ζF is unbounded or F has a fixed point. 4 Advances in Difference Equations Lemma 2.8. Assume that y ∈ C0,T,R,T>0, 1 <α≤ 2. A function u ∈ PCJ is a solution of the antiperiodic boundary value problem C α D ut yt,t∈ 0,T,t/ tk,k 1, 2,...,p, Δu| I ut , Δu| J ut ,k , ,...,p, ttk k k ttk k k 1 2 2.6 u0 uT 0,u0 u T 0, if and only if u is a solution of the integral equation ⎧ p ⎪ t 1 ti ⎪ 1 α−1 1 α−1 ⎪ t − s ysds − ti − s ysds ⎪Γα 2Γα t ⎪ 0 i1 i−1 ⎪ p ⎪ ti ⎪ 1 α−2 ⎪ − T − ti ti − s ysds ⎪ 2Γα − 1 t ⎪ i1 i−1 ⎪ ⎪ p t p ⎪ T − t 1 i ⎪ 2 t − sα−2ysds − 1 T − t J ut ⎪ Γα − i i i i ⎪ 4 1 i ti− 2 i ⎪ 1 1 1 ⎪ p p ⎪ T − t ⎪ 2 J ut − 1 I ut ,t∈ ,t , ⎪ i i i i 0 1 ⎪ 4 i 2 i ⎪ 1 1 ⎪ ⎪ t k ti ⎪ 1 t − sα−1ysds 1 t − sα−1ysds ⎪ i ⎪Γα t Γα t ⎪ k i1 i−1 ⎪ ⎨ p 1 ti k ut 1 α−1 1 ⎪ − ti − s ysds t − ti 2.7 ⎪ 2Γα t Γα − 1 ⎪ i1 i−1 i1 ⎪ ⎪ ti ⎪ α−2 ⎪ × ti − s ysds ⎪ ⎪ ti− ⎪ 1 ⎪ p ⎪ ti ⎪ − 1 T − t t − sα−2ysds ⎪ i i ⎪ 2Γα − 1 t ⎪ i1 i−1 ⎪ ⎪ p ⎪ T − t 1 ti k ⎪ 2 α−2 ⎪ ti − s ysds t − tiJiuti ⎪ Γα − t ⎪ 4 1 i i−1 i ⎪ 1 1 ⎪ p p ⎪ 1 T − 2t ⎪ − T − t J ut J ut ⎪ i i i i i ⎪ 2 i 4 i ⎪ 1 1 ⎪ k p ⎪ ⎪ I u t − 1 I u t ,t∈ t ,t , ≤ k ≤ p. ⎩ i i i i k k 1 1 i1 2 i1 y c ,c ∈ R Proof. Assume that satisfies 2.6 .UsingLemma 2.5, for some constants 0 1 , we have t ut Iαyt − c − c t 1 t − sα−1ysds − c − c t, t ∈ ,t .
Load more

Recommended publications
  • Prediction of Long Non-Coding Rna and Disease Association Using Network Feature Similarity and Gradient Boosting
    Zhang et al. BMC Bioinformatics (2020) 21:377 https://doi.org/10.1186/s12859-020-03721-0 RESEARCH ARTICLE Open Access LDNFSGB: prediction of long non-coding rna and disease association using network feature similarity and gradient boosting Yuan Zhang1,2†, Fei Ye2†,DapengXiong3,4 and Xieping Gao2,5* *Correspondence: [email protected] Abstract †Yuan Zhang and Fei Ye Background: A large number of experimental studies show that the mutation and contributed equally to this work. regulation of long non-coding RNAs (lncRNAs) are associated with various human 2Key Laboratory of Intelligent Computing and Information diseases. Accurate prediction of lncRNA-disease associations can provide a new Processing of Ministry of Education, perspective for the diagnosis and treatment of diseases. The main function of many Xiangtan University, Xiangtan lncRNAs is still unclear and using traditional experiments to detect lncRNA-disease 411105, China 5College of Medical Imaging and associations is time-consuming. Inspection, Xiangnan University, Chenzhou 423000, China Results: In this paper, we develop a novel and effective method for the prediction of Full list of author information is lncRNA-disease associations using network feature similarity and gradient boosting available at the end of the article (LDNFSGB). In LDNFSGB, we first construct a comprehensive feature vector to effectively extract the global and local information of lncRNAs and diseases through considering the disease semantic similarity (DISSS), the lncRNA function similarity (LNCFS), the lncRNA Gaussian interaction profile kernel similarity (LNCGS), the disease Gaussian interaction profile kernel similarity (DISGS), and the lncRNA-disease interaction (LNCDIS). Particularly, two methods are used to calculate the DISSS (LNCFS) for considering the local and global information of disease semantics (lncRNA functions) respectively.
    [Show full text]
  • A Complete Collection of Chinese Institutes and Universities For
    Study in China——All China Universities All China Universities 2019.12 Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities Anhui 安徽 【www.studyinanhui.com】 1. Anhui University 安徽大学 http://ahu.admissions.cn 2. University of Science and Technology of China 中国科学技术大学 http://ustc.admissions.cn 3. Hefei University of Technology 合肥工业大学 http://hfut.admissions.cn 4. Anhui University of Technology 安徽工业大学 http://ahut.admissions.cn 5. Anhui University of Science and Technology 安徽理工大学 http://aust.admissions.cn 6. Anhui Engineering University 安徽工程大学 http://ahpu.admissions.cn 7. Anhui Agricultural University 安徽农业大学 http://ahau.admissions.cn 8. Anhui Medical University 安徽医科大学 http://ahmu.admissions.cn 9. Bengbu Medical College 蚌埠医学院 http://bbmc.admissions.cn 10. Wannan Medical College 皖南医学院 http://wnmc.admissions.cn 11. Anhui University of Chinese Medicine 安徽中医药大学 http://ahtcm.admissions.cn 12. Anhui Normal University 安徽师范大学 http://ahnu.admissions.cn 13. Fuyang Normal University 阜阳师范大学 http://fynu.admissions.cn 14. Anqing Teachers College 安庆师范大学 http://aqtc.admissions.cn 15. Huaibei Normal University 淮北师范大学 http://chnu.admissions.cn Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities 16. Huangshan University 黄山学院 http://hsu.admissions.cn 17. Western Anhui University 皖西学院 http://wxc.admissions.cn 18. Chuzhou University 滁州学院 http://chzu.admissions.cn 19. Anhui University of Finance & Economics 安徽财经大学 http://aufe.admissions.cn 20. Suzhou University 宿州学院 http://ahszu.admissions.cn 21.
    [Show full text]
  • A New Flavonoid from Selaginella Tamariscina
    Available online at www.sciencedirect.com Chinese Chemical Letters 20 (2009) 595–597 www.elsevier.com/locate/cclet A new flavonoid from Selaginella tamariscina Jian Feng Liu a, Kang Ping Xu a, De Jian Jiang a, Fu Shuang Li a, Jian Shen a, Ying Jun Zhou a, Ping Sheng Xu b, Bin Tan c, Gui Shan Tan a,b,* a School of Pharmaceutical Sciences, Central South University, Changsha, Hunan 410013, China b Xiangya Hospital of Central South University, Changsha, Hunan 410008, China c Xiangnan University, Chenzhou, Hunan 423000, China Received 6 October 2008 Abstract 6-(2-Hydroxy-5-acetylphenyl)-apigenin (1), a new flavonoid with a phenyl substituent, was first isolated from Selaginella tamariscina. Its structure was elucidated on the basis of 1D and 2D NMR as well as ESI-HR-MS spectroscopic analysis. # 2009 Gui Shan Tan. Published by Elsevier B.V. on behalf of Chinese Chemical Society. All rights reserved. Keywords: Selaginella tamariscina; Flavonoids; 6-(2-Hydroxy-5-acetylphenyl)-apigenin Selaginella tamariscina is a traditional medicine, which was introduced in Chinese Pharmacopeia (2005 Ed) for the effectiveness in promoting blood circulation [1]. Pharmacological investigation of the genus Selaginella revealed its biological activities of anti-oxidant, anti-virus, anti-inflammation and effects on cardiovascular system protection [2–5]. A number of flavones, phenylpropanoids, alkaloids, organic acids, anthraquinones and steroids have been identified from genus Selaginella. As a continuation of our work, we reported hererin the isolation and structural elucidation of a new flavonoid, 6-(2-hydroxy-5-acetylphenyl)-apigenin (1) from the 75% enthanol extract of S. tamariscina, which is shown in Fig.
    [Show full text]
  • An Improved SOM-Based Method for Multi-Robot Task Assignment and Cooperative Search in Unknown Dynamic Environments
    energies Article An Improved SOM-Based Method for Multi-Robot Task Assignment and Cooperative Search in Unknown Dynamic Environments Hongwei Tang 1,2,*, Anping Lin 3,*, Wei Sun 2 and Shuqi Shi 1 1 Hunan Provincial Key Laboratory of Grids Operation and Control on Multi-Power Sources Area, Shaoyang University, Shaoyang 422000, China 2 College of Electrical and Information Engineering, Hunan University, Changsha 410082, China 3 College of Electronic Information and Electrical Engineering, Xiangnan University, Chenzhou 423000, China * Correspondence: [email protected] (H.T.); [email protected] (A.L.) Received: 24 April 2020; Accepted: 25 June 2020; Published: 26 June 2020 Abstract: The methods of task assignment and path planning have been reported by many researchers, but they are mainly focused on environments with prior information. In unknown dynamic environments, in which the real-time acquisition of the location information of obstacles is required, an integrated multi-robot dynamic task assignment and cooperative search method is proposed by combining an improved self-organizing map (SOM) neural network and the adaptive dynamic window approach (DWA). To avoid the robot oscillation and hovering issue that occurs with the SOM-based algorithm, an SOM neural network with a locking mechanism is developed to better realize task assignment. Then, in order to solve the obstacle avoidance problem and the speed jump problem, the weights of the winner of the SOM are updated by using an adaptive DWA. In addition, the proposed method can search dynamic multi-target in unknown dynamic environment, it can reassign tasks and re-plan searching paths in real time when the location of the targets and obstacle changes.
    [Show full text]
  • University of Leeds Chinese Accepted Institution List 2021
    University of Leeds Chinese accepted Institution List 2021 This list applies to courses in: All Engineering and Computing courses School of Mathematics School of Education School of Politics and International Studies School of Sociology and Social Policy GPA Requirements 2:1 = 75-85% 2:2 = 70-80% Please visit https://courses.leeds.ac.uk to find out which courses require a 2:1 and a 2:2. Please note: This document is to be used as a guide only. Final decisions will be made by the University of Leeds admissions teams.
    [Show full text]
  • Theoretical Investigation the Compounds of Lanthanum Coordinated with Dihydromyricetin
    2019 International Conference on Applied Mathematics, Statistics, Modeling, Simulation (AMSMS 2019) ISBN: 978-1-60595-648-0 Theoretical Investigation the Compounds of Lanthanum Coordinated with Dihydromyricetin Wen-bo LAN1, Chang-ming NIE2, Xiao-feng WANG1, Li-ping HE1, 1 3,* Yu LIU and Yan-bin MENG 1College of Public Health, Xiangnan University, Chenzhou 423043, China 2School of Chemistry and Chemical Engineering, University of South China, Hengyang, 421001 China 3Medical Department, Xiangnan University, Chenzhou 423043, China *Corresponding author Keywords: Dihydromyricetin, Lanthanum, Density functional theory, Binding energy. Abstract. In order to study in depth the complexes formed by dihydromyricetin and lanthanum which may have a good medical effect. Theoretical study of the molecular structure of dihydromyricetin (DMY) compound containing lanthanum were carried out by using density functional theory (DFT) under the B3LYP/6-311G (d, p) level. All the results shown that the coordination compounds of lanthanum with dihydromyricetin (DMY) could form some different molecular modeling, for example, in this article it involved two complexes, one with a ratio of 1:3 (1La:3DMY), the other with a ratio of 1:4 (1La:4DMY). The main parameters of infrared frontier, atomic charge distribution, binding energy, and molecular orbital and energy from the theoretical simulation for La-3DMY and La-4DMY compounds were analyzed and compared with each other. What’s more, this work was expected to provide significant information for understanding the characteristics of La-DMY compounds at the molecular level and offer valuable comprehensive guides for future experiments. Introduction Dihydromyricetin (DHM, Fig. 1), often called ampelopsin, as a major bioactive constituent of rattan tea, belongs to the flavonoid [1-3].
    [Show full text]
  • Technical Program for IWCMC 2020
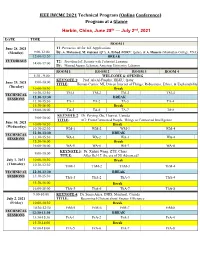
    IEEE IWCMC 2021 Technical Program (Online Conference) Program at a Glance Harbin, China, June 28th — July 2nd, 2021 DATE TIME ROOM 1 June 28, 2021 T1: Pervasive AI for IoT Applications (Monday) 9:00-12:00 By: A. Mohamed, M. Guizani (QU), A. Erbad (HBKU, Qatar), & A. Hussein (Manhattan College, USA) 12:00-13:30 BREAK TUTORIALS T2: Providing IoT Security with Federated Learning 14:00-17:00 By: Mourad Azzam, Lebanese American University, Lebanon ROOM 1 ROOM 2 ROOM 3 ROOM 4 8:30 - 9:00 WELCOME & OPENING KEYNOTE 1: Prof. Ala Al-Fuqaha, HBKU, Qatar 9:00-10:00 June 29, 2021 TITLE: Human-Centric ML Driven Internet of Things: Robustness, Ethics, & Explainability (Tuesday) 10:00-10:30 Break 10:30-12:30 TM-1 TM-2 TM-3 TM-4 TECHNICAL 12:30-13:30 BREAK SESSIONS 13:30-15:30 TA-1 TA-2 TA-3 TA-4 15:30-16:00 Break 16:00-18:00 TA-5 TA-6 TA-7 TA-8 KEYNOTE 2: Dr. Peiying Zhu, Huawei, Canada 9:00-10:00 TITLE: 6G: From Connected People, Things to Connected Intelligence June 30, 2021 10:00-10:30 Break (Wednesday) 10:30-12:30 WM-1 WM-2 WM-3 WM-4 12:30-13:30 BREAK TECHNICAL 13:30-15:30 WA-1 WA-2 WA-3 WA-4 SESSIONS 15:30-16:00 Break 16:00-18:00 WA-5 WA-6 WA-7 WA-8 KEYNOTE 3: Dr. Xinhui Wang, ZTE, China 9:00-10:00 TITLE: After Rel-17, the era of 5G Advanced? July 1, 2021 10:00-10:30 Break (Thursday) 10:30-12:30 ThM-1 ThM-2 ThM-3 ThM-4 TECHNICAL 12:30-13:30 BREAK SESSIONS 13:30-15:30 ThA-1 ThA-2 ThA-3 ThA-4 15:30-16:00 Break 16:00-18:00 ThA-5 ThA-6 ThA-7 ThA-8 9:00-10:00 KEYNOTE 4: Dr.
    [Show full text]
  • Research Article Existence and Ulam Stability of Solutions for Discrete Fractional Boundary Value Problem
    Hindawi Publishing Corporation Discrete Dynamics in Nature and Society Volume 2013, Article ID 459161, 7 pages http://dx.doi.org/10.1155/2013/459161 Research Article Existence and Ulam Stability of Solutions for Discrete Fractional Boundary Value Problem Fulai Chen1 andYongZhou2 1 Department of Mathematics, Xiangnan University, Chenzhou 423000, China 2 School of Mathematics and Computational Science, Xiangtan University, Xiangtan 411005, China Correspondence should be addressed to Fulai Chen; [email protected] Received 28 May 2013; Accepted 9 July 2013 Academic Editor: Shurong Sun Copyright © 2013 F. Chen and Y. Zhou. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. We discuss the existence of solutions for antiperiodic boundary value problem and the Ulam stability for nonlinear fractional difference equations. Two examples are also provided to illustrate our main results. 1. Introduction operator; here, we choose the Banach contraction mapping principle and the Brower fixed-point theorem. Motivated This paper investigates the existence of solutions for antiperi- by the work of the Ulam stability for fractional differential odicboundaryvalueproblemandtheUlamstabilityfor equations [14], in this paper, we also introduce four types nonlinear fractional difference equations: of the Ulam stability definitions for fractional difference Δ () =(+−1,(+−1)) , equations and study the Ulam-Hyers stable and the Ulam- Hyers-Rassias stable. (1) The rest of the paper is organized as follows. In Section 2, ∈[0, ]N , 1<<2, 0 we introduce some useful preliminaries. In Section 3,we consider the existence of solutions for antiperiodic boundary where Δ is a Caputo fractional difference operator, N = value problem of fractional difference equations.
    [Show full text]
  • Beyond the Physiological Role. [Tohoku J. Exp. Med., 2018, 244 (1), 75-81
    Tohoku J. Exp. Med., 2018, 244, 175 Title 175 Retraction Retraction: Nucleophagy in Human Disease: Beyond the Physiological Role. [Tohoku J. Exp. Med., 2018, 244 (1), 75-81. doi: 10.1620/tjem.244.75. Review.] Ming Zhou,1,* Hongwen Ji,2,* Nian Fu,3 Linxi Chen4 and Yong Xia5 1Department of Hematology, Hunan Provincial People’s Hospital, The First Affiliated Hospital of Hunan Normal University, Changsha, China 2Department of Anesthesiology, Transfusion Medicine, Fuwai Hospital, Chinese Academy of Medical Sciences, Peking Union Medical College, Beijing, China 3Department of Gastroenterology, Affiliated Nanhua Hospital, University of South China, Hengyang, China 4Institute of Pharmacy and Pharmacology, Hunan Province Cooperative Innovation Center for Molecular Target New Drug Study, University of South China, Hengyang, China 5Affiliated Hospital of Xiangnan University, Chenzhou, China *These two authors contributed equally to this work. Correspondence: Yong Xia, Affiliated Hospital of Xiangnan University, 25 Renming Road, Chenzhou 423000, Hunan Province, China. Retraction Notice Retracted Review article: Nucleophagy in Human Disease: Beyond the Physiological Role. [Tohoku J. Exp. Med., 2018, 244 (1), 75-81. doi: 10.1620/tjem.244.75.] The above Review article was published online on January 27, 2018. Soon after its publication (on February 1, 2018), Dr. Nian Fu and Prof. Linxi Chen informed the Editor-in-Chief, The Tohoku Journal of Experimental Medicine (TJEM), about serious violation of publication ethics. Indeed, Dr. Nian Fu and Prof. Linxi Chen were astonished to find their names as coau- thors of this Review article, because they were not involved in the submission process of this Review article and they do not know any of other coauthors.
    [Show full text]
  • Snbttatton Letter
    ORIENTAL EDUCATION NETWORK CO., LTD OREN » A 60 Queen Sirikit National Convention Center Zone D, 2nd Floor, D20l/4__= 5, New Rachadapisek Road, Klongtoey, Bangkok 10110 Tel. 0 2229 4477-8, 0 6627 1751, 0 9790 7744 Fax. 0 2229 4479 E-mail: [email protected] Website.- www.thai2ckina.com Snbttatton Letter ,: Regarding Invite to attend OCSC International Education Expo 2018 in Bangkok, ORIENTAL EDUCATION NETWORK CO.XTD Dear Chinese Service Center for Scholarly Exchange, Ministry of Education, P.R. China On behalf of Inviter ORIENTAL EDUCATION NETWORK CO., LTD, Bangkok, it is my pleasure to invite a group of Chinese Service Center for Scholarly Exchange, Ministry of Education, P.R. China to attend OCSC International Education Expo 2018 in Bangkok. The purpose of this visit is to attend OCSC International Education Expo 2018 in Bangkok and visit schools and university in Thailand. We believe this Education Expo is a good chance to enhance your cooperation with institutions in Thailand. The duration of this invitation is from 9th to 13th November 2018. A group will afford all the expense during this visit. The list of the university and name, will attach with this letter. Should you have any query about this invitation please do not hesitate to contact Mr.Kittipong Luywikai, telephone number +66 22294477. We look forward to your visit. Yours Sincerely, <^ Mr. Kittipong Luywikai International Exchange and Cooperation Manager Oriental Education Network Co., Ltd. August 20, 2018 ORIENTAL EDUCATION NETWORK CO., LTD OREN V •-. 60 Queen Sirikit National Convention Center Zone D, 2nd Floor, D20j/4_z 5, New Rachadapisek Road, Klongtoey, Bangkok 10110 Tel.
    [Show full text]
  • The Psychological Impact and Associated Factors of COVID-19 on the General Public in Hunan, China
    Risk Management and Healthcare Policy Dovepress open access to scientific and medical research Open Access Full Text Article ORIGINAL RESEARCH The Psychological Impact and Associated Factors of COVID-19 on the General Public in Hunan, China This article was published in the following Dove Press journal: Risk Management and Healthcare Policy Chunhong Shi, 1 Zhihua Purpose: This study aimed to assess the psychological impact of the COVID-19 pandemic Guo,2 Chan Luo,3 Changbin among the general public in Hunan Province, China, which could help develop psychological Lei, 4 Pan Li1 interventions and mental health programs. This online cross-sectional study recruited 571 participants 1School of Nursing, Xiangnan University, Participants and Methods: Chenzhou 423000, People’s Republic of through snowball sampling between February 2 and February 5, 2020. Data were collected through 2 China; Nursing Department, Changsha a general information questionnaire, the Public Emergency Psychological State Questionnaire, the Health Vocational College, Changsha 410100, People’s Republic of China; 3Nursing Simple Coping Style Questionnaire, and the Public Disease Awareness on COVID-19 Scale. Department, The First AffiliatedHospital of Results: The total mean score of the public emergency psychological state of the sample University of South China, Hengyang 421001, was 0.27 (0.31) points, with only 5.78% of participants (n = 33) developing psychological People’s Republic of China; 4Clinical Medicine Research Center, AffiliatedHospital of distress. Avoidant coping style and disease awareness were weakly positively correlated (rs = Xiangnan University, Chenzhou 423000, 0.257, p < 0.01) and weakly negatively correlated (rs = −0.124, p <0.01) with psychological People’s Republic of China responses, respectively.
    [Show full text]
  • Anxiety and Adaptation of Behavior in Pregnant Zhuang Women During the COVID-19 Pandemic: a Mixed-Mode Survey
    Risk Management and Healthcare Policy Dovepress open access to scientific and medical research Open Access Full Text Article ORIGINAL RESEARCH Anxiety and Adaptation of Behavior in Pregnant Zhuang Women During the COVID-19 Pandemic: A Mixed-Mode Survey This article was published in the following Dove Press journal: Risk Management and Healthcare Policy Yuan Ge1 Purpose: This study explored the impact of COVID-19 on the mental health and adaptation Chunhong Shi 2 of behavior of Zhuang women in China to provide more specific guidance for the social and Bin Wu1 medical practice of pregnant women during public health emergencies. Yannan Liu3 Participants and Methods: This cross-sectional study recruited 446 pregnant Zhuang Ling Chen1 women from obstetric outpatient clinics in four tertiary hospitals and online maternity schools in Nanning, Guangxi, between February 24 and March 1, 2020. Self-designed Yuegui Deng4 questionnaires and the Self-Rating Anxiety Scale were used. 1 School of Nursing, Guangxi University of Results: During the COVID-19 pandemic, the prevalence rate of anxiety among women was Chinese Medicine, Nanning, 530200, People’s Republic of China; 2School of 36.77%, and some adaptation of behavior was observed. Logistic regression analysis showed Nursing, Xiangnan University, Chenzhou, that pregnant women who had an annual household income of less than $7,000, were 423000, People’s Republic of China; primiparous, went out for prenatal examination, wanted to self-monitor during pregnancy 3Nursing School, Hunan University of Medicine, Huaihua, 418000, People’s but did not know how to do it, believed that they should be strictly isolated at home and Republic of China; 4Nursing Department, cancel prenatal examinations, and expected to receive pregnancy healthcare through tele­ The First Affiliated Hospital of Guangxi consultation services showed a higher risk of anxiety.
    [Show full text]