DELAY MANAGEMENT and DISPATCHING in RAILWAYS 272 TWAN DOLLEVOET Passenger Railway Transportation Plays a Crucial Role in the Mobility in Europe
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Talking Book Topics November-December 2016
Talking Book Topics November–December 2016 Volume 82, Number 6 About Talking Book Topics Talking Book Topics is published bimonthly in audio, large-print, and online formats and distributed at no cost to participants in the Library of Congress reading program for people who are blind or have a physical disability. An abridged version is distributed in braille. This periodical lists digital talking books and magazines available through a network of cooperating libraries and carries news of developments and activities in services to people who are blind, visually impaired, or cannot read standard print material because of an organic physical disability. The annotated list in this issue is limited to titles recently added to the national collection, which contains thousands of fiction and nonfiction titles, including bestsellers, classics, biographies, romance novels, mysteries, and how-to guides. Some books in Spanish are also available. To explore the wide range of books in the national collection, visit the NLS Union Catalog online at www.loc.gov/nls or contact your local cooperating library. Talking Book Topics is also available in large print from your local cooperating library and in downloadable audio files on the NLS Braille and Audio Reading Download (BARD) site at https://nlsbard.loc.gov. An abridged version is available to subscribers of Braille Book Review. Library of Congress, Washington 2016 Catalog Card Number 60-46157 ISSN 0039-9183 About BARD Most books and magazines listed in Talking Book Topics are available to eligible readers for download. To use BARD, contact your cooperating library or visit https://nlsbard.loc.gov for more information. -

March Wk01 Combined ARB
ILLINOIS WORKERS' COMPENSATION COMMISSION PAGE 1 C A S E H E A R I N G S Y S T E M MAUREEN PULIA 004 ARBITRATION CALL FOR QUINCY 42 004 ON 3/3/2021 SEQ CASE NBR PETITIONER NAME RESPONDENT NAME C O N N E C T E D C A S E S ACCIDENT PETITIONER ATTORNEY RESPONDENT ATTORNEY ↓ ↓ ↓ ↓ DATE ************************************************************************************ 1 03WC 03770 BUTLER, APRIL ADECCO EMPLOYMENT SERVICE 2/12/2011 THOMAS R LICHTEN NYHAN BAMBRICK KINZI 2 06WC 44900 TAYLOR, SHARON SOI, ILLINOIS VETERANS HO 4/9/2027 BERG & ROBESON ASSISTANT ATTORNEY G 3 08WC 23817 DORSEY, SHEILA ILLINI COMMUNITY HOSPITAL 8/1/2011 LAMARCA LAW OFFICES, PC NYHAN BAMBRICK KINZI 4 09WC 24313 STAPP, TROY RAIL CREW XPRESS 8/10/1930 THOMAS R LICHTEN 5 09WC 36074 WEMHOENER, SANDY K ILLINOIS VETERAN HOMES C O N N E C T E D C A S E S 7/4/2021 BERG & ROBESON ASSISTANT ATTORNEY G 09WC036075 12WC010594 14WC012250 6 09WC 49401 TAYLOR, SHARON ILLINOIS VETERANS HOME 5/7/2011 BERG & ROBESON ASSISTANT ATTORNEY G 7 10WC 45351 MEYER, WILLIAM G CCE C O N N E C T E D C A S E S 8/2/2028 THOMAS R LICHTEN BRADY, CONNOLLY & MA 10WC045352 10WC045353 8 12WC 22789 SIMMONS, RICHARD IDOT DISTRICT 6 12/4/2011 RIDGE & DOWNES LLC ASSISTANT ATTORNEY G 9 12WC 43805 CLARK, BRANDY LEE BLESSING HOSPITAL 12/9/2024 THOMAS R LICHTEN NYHAN BAMBRICK KINZI 10 13WC 04017 MORRISON, ANDREW C ILLINOIS VETERAN'S HOME C O N N E C T E D C A S E S 12/11/1930 GERALD TIMMERWILKE ASSISTANT ATTORNEY G 13WC004018 11 14WC 00548 WILLIS, CYNTHIA S NIEMANN FOODS INC KANOSKI BRESNEY SCHOLZ LOOS PALMER E 12 14WC 38789 SAXBERY, MARY A QUINCY PUBLIC SCHOOL DIST KATZ FRIEDMAN EAGLE ET AL BRYCE DOWNEY & LENKO 13 14WC 40062 BLENTLINGER-MARSHALL, NAN ST OF IL, QUINCY VETERANS CONNOR LAW OFFICES ASSISTANT ATTORNEY G 14 15WC 09029 MOON, CHANDLER DOT FOODS INC STEPHEN P. -

Hearing Dates Are Subject to Continuance Or Cancellation
Hearing dates are subject to continuance or cancellation. Dockets are subject to daily update. Check this site regularly for updates or changes. This docket is current as of 9/22/2017. To Search for Information such as case number or attorney name click on "Binocular" or "Find". After entering the information you want in the "Find What", click on "Find". To continue searching, click on "Find Again". Search by attorney name and firm name/agency. -

See Who Attended
Company Name First Name Last Name Job Title Country 24Sea Gert De Sitter Owner Belgium 2EN S.A. George Droukas Data analyst Greece 2EN S.A. Yannis Panourgias Managing Director Greece 3E Geert Palmers CEO Belgium 3E Baris Adiloglu Technical Manager Belgium 3E David Schillebeeckx Wind Analyst Belgium 3E Grégoire Leroy Product Manager Wind Resource Modelling Belgium 3E Rogelio Avendaño Reyes Regional Manager Belgium 3E Luc Dewilde Senior Business Developer Belgium 3E Luis Ferreira Wind Consultant Belgium 3E Grégory Ignace Senior Wind Consultant Belgium 3E Romain Willaime Sales Manager Belgium 3E Santiago Estrada Sales Team Manager Belgium 3E Thomas De Vylder Marketing & Communication Manager Belgium 4C Offshore Ltd. Tom Russell Press Coordinator United Kingdom 4C Offshore Ltd. Lauren Anderson United Kingdom 4Cast GmbH & Co. KG Horst Bidiak Senior Product Manager Germany 4Subsea Berit Scharff VP Offshore Wind Norway 8.2 Consulting AG Bruno Allain Président / CEO Germany 8.2 Consulting AG Antoine Ancelin Commercial employee Germany 8.2 Monitoring GmbH Bernd Hoering Managing Director Germany A Word About Wind Zoe Wicker Client Services Manager United Kingdom A Word About Wind Richard Heap Editor-in-Chief United Kingdom AAGES Antonio Esteban Garmendia Director - Business Development Spain ABB Sofia Sauvageot Global Account Executive France ABB Jesús Illana Account Manager Spain ABB Miguel Angel Sanchis Ferri Senior Product Manager Spain ABB Antoni Carrera Group Account Manager Spain ABB Luis andres Arismendi Gomez Segment Marketing Manager Spain -

Listed Alphabetically
Listed Alphabetically Please arrive at 540 W Madison Street 20 minutes prior to your start time. Avoid the lines on event day and visit Packet Pick-Up on Friday or Saturday in the Presidential Towers lobby. When your wave number is called, please report to the Climber Line-Up Area at 540 W Madison Street. You will then be escorted, with your wave, to Presidential Towers. Bib No Wave Start Time Towers Last Name First Name Team Name 618 25 9:10 a.m. X2 Abraham Ryanne Assurance Rock Stars 254 10 7:55 a.m. X4 Acevedo Mildred Dream Seekers 1471 POLICE 12:15 p.m. X4 Acevedo Janete The Band of Brothers 1386 53 11:35 a.m. X4 Acker Ralph 76 2 7:15 a.m. X4 Adams Rachael Mesirow IT Climbs 1074 41 10:35 a.m. X4 Adams Todd The Adams Family 1075 41 10:35 a.m. X4 Adams Sheridan The Adams Family 1100 41 10:35 a.m. X4 Adams Loleta Move Your Body 50 + 1126 42 10:40 a.m. X4 Adams Robin Climb for Nick 395 16 8:25 a.m. X2 Adams Smith Kristen KSD 835 34 9:55 a.m. X4 Adamski Sabina Cant Stop Stairing 1120 42 10:40 a.m. X4 Aguero Andres Victorious Lungs 974 37 10:15 a.m. X4 Aguilar Sonia Team Medtronic 1302 50 11:20 a.m. X4 Albergo Danielle Protiviti 1166 44 10:50 a.m. X4 Alcantar Luna Ramiro 260 10 7:55 a.m. X4 Aleman Claudia Dream Seekers 255 10 7:55 a.m. -

Active-Warrants-02022018.Pdf
Last Name First Name Middle Name Date of Birth Warrant Type Violations ABBOTT PATRICK REYES 11/19/1993 MISD FTA ON SPEEDING ABDELLATIF FARES A 3/7/1982 MISD FTA-SPEEDING ABRAHAM CHRYN MARIE 7/22/1957 MISD FTOCO VAHCL CBO ABUDARAHIM MESHARI MOHAMMED 12/22/1992 MISD FTA-NO PROOF LIABILITY INS-ASP, SPEEDING ACHORD SHANNA BOUTTE 9/19/1982 MISD FTA-NO CHILD RESTRAINT ACOSTA AUGUSTIN SANTOS JR 9/24/1965 MISD FTA-SPEEDING, DWLS CBO ADAMS CALVIN DEMARK 1/5/1972 MISD FTOCOX2-DWI,IMPLIED CONSENT,POSS OF MARIJUANA, DISORDERLY CONDUCT ADAMS SHANNON RENE 3/30/1971 MISD FTOCOX2-NO DL ADAMS RAY CHARLES 6/14/1981 MISD FTOCO ON DWDLS ADANI ANTHONY JAMES 8/28/1984 MISD FTA SPEEDING CBO AGUILAR GABRIEL ABILA 2/28/1966 FEL FTOCO-CHILD SUPPORT CBO AGUILAR VICTOR RUIZ 7/23/1983 MISD FTA/NO DL CBO AGUILAR-GARZA JESUS E 11/2/1987 MISD FTA-NO DL, NO CHILD RESTRAINT AGUILAR-MARTINEZ GERMAN RAUL 12/2/1983 MISD FTA-NO DL, NO PROOF OF LIABILITY INS-ASP, NO SEAT BELT AGUILAR-TELLO WENDY JANET 12/5/1986 MISD FTA,NO DL, NO PROOF INS, CBO AHN JIN HWAN 8/12/1964 MISD FTA-NO DL, SPEEDING, NO PROOF OF LIABILITY INS-ASP CBO AIKIN AUSTIN KYLE 3/9/1992 MISD FTOCO,SPEEDING/DWLS AKIN DUSTIN KEITH 4/2/1984 CS FTOCO- CHILD SUPPORT CASH BOND AKIN GLENN ALLEN 9/7/1962 MISD FTOCO FTA NO INSURANCE NO DL AKINS PATRICA / / MISD FTA-FAILURE TO VACATE CBO ALANIZ CHELSEA MARIE 5/1/1989 MISD FTA-NO VEHICLE LICENSE (TAGS) CBO ALANIZ CHRISTOPHER LEE 12/25/1984 FEL PROB VIOL ON B&E, REVO X2 ALBARRAN CORIA JONATHAN 5/23/1985 MISD ftoco ALBERTY ASHLY SHANAYE 12/7/1991 MISD FTOCO,FTA,CURFEW VIOLATION,CBO -

Commencement Flyer
FPO UNIVERSITY OF MIAMI COMMENCEMENT2020 SPRING AND SUMMER UNIVERSITY OF MIAMI COMMENCEMENT2020 SPRING AND SUMMER Graduate School School of Architecture College of Arts and Sciences Patti and Allan Herbert Business School School of Communication School of Education and Human Development College of Engineering Rosenstiel School of Marine and Atmospheric Science Leonard M. Miller School of Medicine Phillip and Patricia Frost School of Music School of Nursing and Health Studies Message from the President JULIO FRENK To the Class of 2020, Congratulations! You are now prepared to undertake the next stage of your personal and professional development. Your education has equipped you with a unique skill set enriched by the experiences you have gained here at the University of Miami. The relationships you have forged with faculty, advisers, and fellow students have not only strengthened our community, but will undoubtedly be a source of community and strength throughout your career. I have always had an unwavering belief in your ability to persevere, but you have truly exhibited in an outstanding way the characteristics of caring and resilient ’Canes in the face of challenges such as hurricanes and now, the COVID-19 pandemic. This unprecedented emergency, which for the time being has transformed learning and upended life as we know it, forced the postponement of our spring commencement ceremonies until December. But that in no way affects your degree status, nor our immense pride in your accomplishments. I know you must feel frustration and disappointment at not being able to celebrate together at this time. If you choose to return in December, we will celebrate then. -

Closely Intertwined for Centuries
IllusterMarch 2021 How can we make sure Utrecht stays accessible, healthy and inclusive? Creating tomorrow, together with Mapping air quality our alumni UNIVERSITY AND CITY Closely intertwined for centuries Professor of University History Leen Dorsman explains FOREWORD Anniversary Contents during a pandemic The inter- 22 ‘I decided to his year, Utrecht University (UU) and connected UMC Utrecht will be celebrating 385 years only write things of science and academia in Utrecht. Due to COVID 19 all the get-togethers and 10 nature of I understood celebrations will have to be held in an Talternative manner or be postponed until later. VR headsets for University myself’ What a contrast to the festivities in 1986. It was my first ‘real’ job: organising the celebration of the 350th anniver- patients with sary of our university. In addition to experienced staff and city and clever academics, young people nearing graduation — brain damage myself included — were asked to help with the organisa- tion as well. I think of that period often. It was hard graft: Rutger Bregman a hectic schedule, deadlines, juggling multiple tasks and Alumnus of the Year working late often. But there was also plenty of humour and a strong sense of camaraderie. I gained lifelong friendships during that time. At the opening, Queen Beatrix specifically wanted to meet the young employees. We were so very proud. When I look at the picture taken of us together, it always brings back happy memories. Like then, the current anniversary year is Publication details 12 4 The big picture all about the connection to society, 6 Short with ‘Creating tomorrow together’ Illuster is a Utrecht University and Utrecht University Fund The Utrecht publication. -
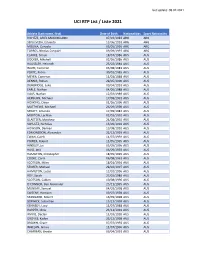
UCI RTP List / Liste 2021
last update: 08.07.2021 UCI RTP List / Liste 2021 Athlete (Last name, first) Date of Birth Nationalities Sport Nationality RICHEZE, ARIEL MAXIMILIANO 07/03/1983 ARG ARG SEPULVEDA, Eduardo 13/06/1991 ARG ARG MOLINA, Gonzalo 05/05/1995 ARG ARG TORRES, Nicolas Exequiel 09/09/1997 ARG ARG CLARKE, Simon 18/07/1986 AUS AUS DOCKER, Mitchell 02/10/1986 AUS AUS HAUSSLER, Heinrich 25/02/1984 AUS AUS WURF, Cameron 03/08/1983 AUS AUS PORTE, Richie 30/01/1985 AUS AUS MEYER, Cameron 11/01/1988 AUS AUS DENNIS, Rohan 28/05/1990 AUS AUS DURBRIDGE, Luke 09/04/1991 AUS AUS EARLE, Nathan 04/06/1988 AUS AUS HAAS, Nathan 12/03/1989 AUS AUS HEPBURN, Michael 17/08/1991 AUS AUS HOSKING, Chloe 01/10/1990 AUS AUS MATTHEWS, Michael 26/09/1990 AUS AUS SPRATT, Amanda 17/09/1987 AUS AUS MORTON, Lachlan 02/01/1992 AUS AUS GLAETZER, Matthew 24/08/1992 AUS AUS SCHULTZ, Nicholas 13/09/1994 AUS AUS HOWSON, Damien 13/08/1992 AUS AUS EDMONDSON, Alexander 22/12/1993 AUS AUS EWAN, Caleb 11/07/1994 AUS AUS POWER, Robert 11/05/1995 AUS AUS HINDLEY, Jai 05/05/1996 AUS AUS HAIG, Jack 06/09/1993 AUS AUS HAMILTON, Christopher 18/05/1995 AUS AUS COOKE, Carol 06/08/1961 AUS AUS SCOTSON, Miles 18/01/1994 AUS AUS STORER, Michael 28/02/1997 AUS AUS HAMILTON, Lucas 12/02/1996 AUS AUS ROY, Sarah 27/02/1986 AUS AUS SCOTSON, Callum 10/08/1996 AUS AUS O'CONNOR, Ben Alexander 25/11/1995 AUS AUS MUNDAY, Samuel 04/03/1998 AUS AUS SWEENY, Harrison 09/07/1998 AUS AUS STANNARD, Robert 16/09/1998 AUS AUS BERWICK, Sebastian 15/12/1999 AUS AUS KENNEDY, Lucy 11/07/1988 AUS AUS HARPER, Chris 23/11/1994 -

City of Memphis Employee Salaries August 2021 Division Employee
City Of Memphis Employee Salaries August 2021 Division Employee Name Job Title Annual Salary Hourly/Per Category Event Rate City Attorney Little, Brandon Claims Analyst N/A 15.00 Part-Time City Attorney Fulton, Eddie Internship Urban Fellow N/A 12.00 Part-Time City Attorney Garvins, Tracie Denise Permits_Licenses Spec N/A 15.00 Part-Time City Attorney Lee, Karen Yvette Permits_Licenses Spec N/A 15.00 Part-Time City Attorney Felder, Vivian A. Administrative Asst 40,562.34 N/A Regular City Attorney Kirkwood, LaKenya Administrative Asst 40,562.34 N/A Regular City Attorney Bearden, Joyce Winton Administrative Asst 40,562.34 N/A Regular City Attorney Rodgers, Delthia Alarm Billing Spec 36,241.92 N/A Regular City Attorney Lacy, Kirby Alarm Data Spec 36,241.92 N/A Regular City Attorney Bradley, Rickey A. Alarm Project Analyst 47,435.96 N/A Regular City Attorney Chen, Lan Asst City Attorney 70,709.08 N/A Regular City Attorney Fletcher, Joseph M Asst City Attorney 80,000.18 N/A Regular City Attorney Gibbons, William L. Jr. Asst City Attorney 76,748.88 N/A Regular City Attorney Kelley, Christopher Lawrence Asst City Attorney 70,709.08 N/A Regular City Attorney Burrow, Latonya Sue Chief Ethics Officer 49,673.52 N/A Regular City Attorney Bibbs, Carlos A. City Attorney Asst Sr 99,346.78 N/A Regular City Attorney Chambliss, Prince C. Jr. City Attorney Asst Sr 99,346.78 N/A Regular City Attorney Davis, Barbaralette G. City Attorney Asst Sr 106,870.40 N/A Regular City Attorney Foster, Freeman B City Attorney Asst Sr 97,580.60 N/A Regular City Attorney Graham, George W. -

Commencement Committees
Commencement MAY 2021 WELCOME FROM THE PRESIDENT Dear Friends: It is with a mixture of happiness, pride, and confidence that I write to you on this occasion of the culmination of your years of effort and achievement at the University of Connecticut. Many times in the past 12 months I have had reason to recall the observation of the Greek Stoic philosopher Epictetus: “Happiness and freedom begin with one principle: some things are within your control, and some are not.” This is a principle we can truly say has been affirmed for everyone in the world since the spring of 2020. Certainly, it is a principle that was not lost on you, as you responded to events outside your control with the creativity, determination, and perseverance that came to characterize UConn during this time. Great challenges beget great achievements, and your achievement as students here shine as brightly as any in the 140- year history of our University. You now continue your journey in the world not just prepared, but empowered: empowered by the knowledge that you have it within yourself to face any obstacle, and overcome it. This is a special class, its ranks filled with scholars of all disciplines and leaders on issues from climate action to racial justice. One of the pleasures I look forward to in the coming years is learning of how you will apply your UConn experience to transforming our world – hopefully, learning about it from you in person, on visits back to your alma mater. As we move closer toward a return to a semblance of life as we knew it before the pandemic, I know it will become easier to put the last year into the context of your entire time at UConn. -

SUSTAINABLE LAND MANAGEMENT and RESTORATION in the MIDDLE EAST and NORTH AFRICA REGION Issues, Challenges, and Recommendations
SUSTAINABLE LAND MANAGEMENT AND RESTORATION IN THE MIDDLE EAST AND NORTH AFRICA REGION Issues, Challenges, and Recommendations Fall 2019 Environmnt, Nturl Rsourcs & Blu Econom 64270_SLM_CVR.indd 3 11/6/19 12:38 PM SUSTAINABLE LAND MANAGEMENT AND RESTORATION IN THE MIDDLE EAST AND NORTH AFRICA REGION ISSUES, CHALLENGES, AND RECOMMENDATIONS 10116-SLM_64270.indd 1 11/19/19 1:37 PM © 2019 International Bank for Reconstruction and Development/The World Bank 1818 H Street NW Washington, DC 20433 Telephone: 202-473-1000 Internet: www.worldbank.org This work is a product of the staff of The World Bank with external contributions. The findings, interpretations, and conclusions expressed in this work do not necessarily reflect the views of The World Bank, its Board of Executive Direc- tors, or the governments they represent. The World Bank does not guarantee the accuracy of the data included in this work. The boundaries, colors, denomina- tions, and other information shown on any map in this work do not imply any judgment on the part of The World Bank concerning the legal status of any territory or the endorsement or acceptance of such boundaries. Rights and Permissions The material in this work is subject to copyright. The World Bank encourages dissemination of its knowledge, this work may be reproduced, in whole or in part, for noncommercial purposes as long as full attribution to this work is given. Attribution—Please cite the work as follows: World Bank. 2019. Sustainable Land Management and Restoration in the Middle East and North Africa Region—Issues, Challenges, and Recommendations. Washington, DC. Any queries on rights and licenses, including subsidiary rights, should be addressed to: World Bank Publications The World Bank Group 1818 H Street NW Washington, DC 20433 USA Fax: 202-522-2625 10116-SLM_64270.indd 2 11/19/19 1:37 PM TABLE OF CONTENTS Acknowledgments .