DOCSLIB.ORG

Barkochba Or 20Q (Twenty Questions) – the Game Against the Magic of Words Laszlo Pitlik, Laszlo Pitlik (Jun), Matyas Pitlik, Marcell Pitlik (MY-X Team)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Barkochba Or 20Q (Twenty Questions) – the Game Against the Magic of Words Laszlo Pitlik, Laszlo Pitlik (Jun), Matyas Pitlik, Marcell Pitlik (MY-X Team) Barkochba or 20Q (Twenty Questions) – The game against the magic of words Laszlo Pitlik, Laszlo Pitlik (jun), Matyas Pitlik, Marcell Pitlik (MY-X team) Abstract: This article demonstrates a similarity-based rule system for evaluating 20Q-games. 20Q- games and taxonomies (like plant and/or animal taxonomies) are useful supporters in order to be capable of explaining what is an expert system, why a single abstraction (like human words) can not be defined with an arbitrary exactness, why an appropriate definition has to have two layers: one for a direct description and an other one about exclusions of parallel terms/objects (like in the taxonomies). The KNUTH’s principle expects that each real knowledge-like phenomenon should be transformed into source code. Expert systems are the lowest level of structured descriptions being prepared for deriving words like in a 20Q-game. Keywords: taxonomy, expert system, similarity, evaluation rule set Introduction This paper is the newest part of the series about experiences of the QuILT-based education processes. Previous articles can be downloaded here: • https://miau.my-x.hu/miau/quilt/Definitions_of_knowledge.docx + annexes like: o https://miau.my-x.hu/miau/quilt/demo_questions_to_important_messages.docx o https://miau.my-x.hu/mediawiki/index.php/QuILT-IK045-Diary o https://miau.my-x.hu/mediawiki/index.php/Vita:QuILT-IK045-Diary o https://miau.my-x.hu/mediawiki/index.php/QuILT-IK059-Diary o https://miau.my-x.hu/mediawiki/index.php/Vita:QuILT-IK059-Diary • https://miau.my-x.hu/miau/quilt/reality_driven_education.docx + annexes like: o https://miau.my-x.hu/miau/quilt/chained-translations-legal-slang.docx o https://miau.my-x.hu/miau/quilt/demo_chained_translations.docx o https://miau.my-x.hu/miau/quilt/demos_chained_translations.docx o https://miau.my-x.hu/miau/quilt/forum_details.docx o https://miau.my-x.hu/mediawiki/index.php/QuILT-IK057-Diary o https://miau.my-x.hu/mediawiki/index.php/Vita:QuILT-IK057-Diary • https://miau.my-x.hu/miau/quilt/Exercises_for_critical_thinking_and_doing.docx • https://miau.my-x.hu/miau/quilt/st1_all.docx • (https://miau.my-x.hu/miau/quilt/20Q.docx) The running experimental education (where the experimental characteristics belongs to the international frames and not for the methodology as such) tries to support the shifting of paradigms from the classic teaching (e.g. based on the magic of words) towards to AI-based approaches where the KNUTH’s principle can be realized in an objective way. The first attempts about the definition of the word of knowledge made possible to derive that neither a good definition could be created, nor the huge volume of parallel definition could be ranked – because no rule system for evaluation of the available definitions could be created. Parallel, there are a lot of log-data about the Moodle-activities of the Students and there is a valid question too: Who is the best Student? Yet, there are no valid rule systems to evaluate Student’s activities. In ideal case, a valid rule system would be created by Students so, that each Student would suggest at least one variable being objective measurable about the activities of Students. This question about the best Student should always have a solution – in the most cases a subjective one (c.f. general scoring systems in the schools – without the using of the anti-discriminative principle: Each Student can have the same evaluation value based on a lot of performance variables (like subjects/competences). As it can be seen in a clear way: the basic problem is (in both cases like log-data and/or set of potential definitions) the lack of the objective/valid rule systems because this makes impossible to handle problems in a target-oriented/objectivized way. About the 20Q-games in general In case of the question “What is the number between 1-100 being chosen in a randomized way?”, the mathematical interpretation delivers a clear answer: https://math.stackexchange.com/questions/512994/guessing-a-number-between-1-and-100-in-7- guesses-or-less - The maximal number of the questions is 7. If somebody derive the numbers of the necessary questions based on the binary approximation for 7 digits with 0 or 1 for each guessable number between 1-100 and these numbers will be added, then we have a lowest sum of questions needed for each guessing from 1 to 100 (step=1). Assumed, that this is a real optimum (=minimum of the sum of the needed questions), then we have a chance to define the mathematics compared e.g. to the social sciences and/or natural/physical sciences. We have already a definition about science/knowledge from KNUTH. A further definition for parts of the science as such can be created as follows: • A problem is a mathematical problem, if the best solution(s) can be derived based on one single evaluation scale (like sum of each necessary questions). • If we could define more than one ranking scale for evaluation of the alternative solutions, then we might not speak about mathematics. In case of the guessing game above-described we could search for the best solution for human beings where not only the total sum of the needed question is a variable being capable of describing expected situation, but it would also be possible to say: the more a strategy leads to wins the better is the strategy. The above- outlined binary strategy is a kind of symmetrical strategy. However, we could create asymmetrical strategies too: e.g. 1. question: Has the searched number just 1 digit? And if we have an answer “YES”, then we will win compared to the binary strategy in case of the lowest values. Similar questions delivering useful asymmetries are e.g. Is the value a prime number? or Contains the value a zero? or each kind of the partibility can lead to the expected effects in the first (or further) level(s). It is important each not pure binary strategy should be defined in advance. Strategies can have mixed characteristics – it means they can combine binary and not binary (symmetrical and asymmetrical) questions. Parallel to the number/ratio of win- positions (compared to the binary strategy), it is also possible to derive the differences between the number of questions for binary and not-binary strategies. The partial rule would be the more is the difference the better is the strategy. We can probably define a lot of further evaluation variables. So, we have a multilayered evaluation problem needing an aggregated evaluation scale for deriving the best strategies. The natural and social sciences can be classified just here and now: o If the multilayered variable come from human beings (it means the variables/words are described in a high abstraction level like knowledge, competence, etc.), then we should speak about social sciences. o If the variables can be measured (like temperature, pressure, etc.), then we should speak about natural sciences. o (If a variable set has both types of the variables, then we can speak about interdisciplinarity.) o (If the measurable variables use terms belonging to human beings like price, income, etc., then we could speak about economics what means economics could belong rather to the natural sciences, than to the social sciences – or even it is a kind of multidisciplinary set of problems.) Relevant question: Are the Wikipedia “definitions” (especially compared to each other) more exact/precise than the above-derived definition based on one single characteristic concerning the used terminology (the type of variables/words/phenomena) or the magic of words can be observed in the single definitions in Wikipedia compared to the above-outlined definition-system where each definition has two layers: a direct one (describing the word as such) and an indirect one (excluding each other parallel terms): • https://en.wikipedia.org/wiki/Social_science (incl. economics) • https://en.wikipedia.org/wiki/Natural_science The 20Q-game can be seen as a kind of generalized version of the guessing game for numbers where the number of the potential solutions can be unlimited. In a limited case of words (see partial taxonomies) it is relevant to ensure, that each question makes the number of the potential solutions step by step fewer. If the number of the potential options in case of a taxonomy in each level is the same value (c.f. Kingdom / Division / Class / Subclass / Series (Order) / Family / Genus / Species / Varieties), and this value would be the 7, then we could speak about a numeral system of the base of 7. The taxonomies can not ensure the above-mentioned sameness. The taxonomies are a kind of asymmetric question systems compared to the above-outlined binary question system as mathematical optimum for searching numbers. Relevant remark: The 20Q-game needs question being answerable with yes or no, but this expectation can not enforce to handle in a binary way: e.g. Is the searched animal a vertebrate animal? (yes/no). BUT: we do not know about relationships to the other options in the DIVISION/PHYLUM level (c.f. https://www.toppr.com/guides/biology/diversity-in-living- organisms/animal-kingdom/). Conclusion: The taxonomy experts could not create a binary (question) system for centuries – not a single asymmetrical one. But a kind of approximately symmetric approach could be created in case of the taxonomies tending to be a numeral system on the base of higher than 2: If somebody knows how many objects are totally available, then on each level (digit), an estimation can be made e.g. what kind of divisions (phylum) together covers ca. the one half of the objects? This aggregated way can be used level by level in the taxonomy.
Load more

Recommended publications
  • 12 Janvier.Indd
    SALUT LES JEUNES! POUR LES PETITS The rule of thumb we all learned when teaching our youngest language learners is that the length of any activity should be calculated by one minute per one year of age of our students. It is a pretty reliable measure, and, as we have noticed recently, the ability of children to focus seems to be weakening with the constant exposure to small bites of information on television and other electronic media. We need to be able to provide multiple activities for a class of very young students, so it is helpful to have a bag of tricks on hand to resort to in order to keep our younger classes moving. The following are two quick games that can be incorporated into your young classes—and they work with older students as well! PAS MOI! My fi rst graders never tire of this game! The only materials you need are enough index cards for the class. Write on all but one: “PAS MOI” and on one “C’EST MOI.” Once you have made the cards, they are available for the rest of the year! LINGUISTIC GOAL: Re- inforcement of “IL S’APPELLE...” and “ELLE S’APPELLE....” THE GAME: Choose one student to do the guessing. Distribute cards to ev- eryone else, making sure they don’t show anyone what is on the card. Folding cards in half helps. The student guessing has three chances (or as many as you wish) to guess who has the C’EST MOI card. Students must use correctly “IL” and “ELLE” and French names if you have assigned them.
    [Show full text]
  • Wee Deliver: the In-School Postal Service. an Introductional Guide to the Postal Service's Wee Deliver In-School Literacy Program
    DOCUMENT RESUME ED 448 442 CS 217 256 TITLE Wee Deliver: The In-School Postal Service. An Introductional Guide to the Postal Service's Wee Deliver In-School Literacy Program.. INSTITUTION Postal Service, Washington, DC. PUB DATE 1997-00-00 NOTE 44p. PUB TYPE Guides Classroom Teacher (052) EDRS PRICE MF01/PCO2 Plus Postage. DESCRIPTORS Elementary Education; Job Skills; *Letters (Correspondence); *Literacy; *Reading Skills; *School Activities; *Writing (Composition) IDENTIFIERS *Post Office ABSTRACT Suggesting that schools can provide valuable reading and writing practice for their students through the implementation of a school post office program, this booklet describes the United States Postal Service's "Wee Deliver" program and provides some materials to get the program started. Participants may model their school after a town by naming streets and assigning addresses. Jobs can then be posted and filled through an application and interview process, with students selected based on achievement and attendance, thereby strengthening student motivation to do well. Students will learn real life skills by performing tasks, being on time for work and developing teamwork. Contains 41 references, a sample news release, application, and employment examination, and sample letter formats and certifications. (EF) Reproductions supplied by EDRS are the best that can be made from the original document. CS I I An introductional guide to the Postal Service's Wee Deliver In-School Literacy Program U.S. DEPARTMENT OF EDUCATION Office of Educational Research and Improvement EDUCATIONAL RESOURCES INFORMATION CENTER (ERIC) This document has been reproduced as received from the person or organization originating it. Minor changes have been made to improve reproduction quality.
    [Show full text]
  • 24 More Corporate Party Games
    24 More Corporate Party Games Loosen up that necktie. It’s time for fun. Games are great for corporate gatherings because they can work as icebreakers and encourage players to mingle. They force people to loosen up and can help you realize the goal of your event. Plus, they will give participants something to giggle with their colleagues for years to come. You simply cannot have too many corporate party games in your back pocket. Company anniversaries, annual outings, VIP birthdays, holidays and other special occasions are going to populate your calendar, and here are some more ideas to help you celebrate. Everyone in a large group of professionals can enjoy these games: co-workers, clients, and even senior staff. Consider the guest list and have a few games (or 24) up your sleeve. Need a little help? Strategic Event Design specializes in helping you achieve the goal of your event, whether that is closing a sale or simply having a little fun. We work with you and your staff to come up with customized games and events that help achieve your goal. Find out more at StrategicEventDesign.com. 1. Blobs and Lines GREAT FOR: AN EARLY MORNING ICEBREAKER This “get to know you” game would be appropriate for any group of people, especially in an office setting. This is an easy format that encourages people get to know each other quickly. The game leader has a list of ways to gather in blobs or line up. It could be lining up in order of birthday, or alphabetically in order of last name.
    [Show full text]
  • Hat Guessing Games
    Hat Guessing Games Steve Butler∗ Mohammad T. Hajiaghayi† Robert D. Kleinberg†‡§ Tom Leighton†¶ Abstract Hat problems have become a popular topic in recreational mathematics. In a typical hat problem, each of n players tries to guess the color of the hat they are wearing by looking at the colors of the hats worn by some of the other players. In this paper we consider several variants of the problem, united by the common theme that the guessing strategies are required to be deterministic and the objective is to maximize the number of correct answers in the worst case. We also summarize what is currently known about the worst-case analysis of deterministic hat-guessing problems with a finite number of players. Key words: hat game; deterministic strategies; sight graph; Tutte-Berge formula; hypercube AMS Mathematics Subject Classification: 91A12; 05C20 1 Introduction Consider the following game. There are n distinguishable players and one adversary. The adversary will place on the heads of the players hats of k different colors, at which point players are allowed to see all hats but their own. No communication is allowed. Each player then makes a private guess as to what hat they are wearing. The goal of the players is to maximize the number of correct guesses. To help players maximize their correct guesses, the players are allowed to meet before the hats are placed on their heads and to determine a public deterministic strategy (public in that everyone, including the adversary, knows the strategy and deterministic in that the guesses are determined ∗Department of Mathematics, University of California, San Diego, La Jolla, CA 92093, U.S.A., Email: [email protected].
    [Show full text]
  • Hundreds of College Athletes Were Asked to Think Back: "What Is Your Worst Memory from Playing Youth and High School Sports?"
    What Makes A Nightmare Sports Parent -- And What Makes A Great One Hundreds of college athletes were asked to think back: "What is your worst memory from playing youth and high school sports?" Their overwhelming response: "The ride home from games with my parents." The informal survey lasted three decades, initiated by two former longtime coaches who over time became staunch advocates for the player, for the adolescent, for the child. Bruce E. Brown and Rob Miller of Proactive Coaching LLC are devoted to helping adults avoid becoming a nightmare sports parent, speaking at colleges, high schools and youth leagues to more than a million athletes, coaches and parents in the last 12 years. Those same college athletes were asked what their parents said that made them feel great, that amplified their joy during and after a ballgame. Their overwhelming response: "I love to watch you play." There it is, from the mouths of babes who grew up to become college and professional athletes. Whether your child is just beginning T-ball or is a travel-team soccer all-star or survived the cuts for the high school varsity, parents take heed. The vast majority of dads and moms that make rides home from games miserable for their children do so inadvertently. They aren't stereotypical horrendous sports parents, the ones who scream at referees, loudly second-guess coaches or berate their children. They are well-intentioned folks who can't help but initiate conversation about the contest before the sweat has dried on their child's uniform. In the moments after a game, win or lose, kids desire distance.
    [Show full text]
  • Gameplay Fun!
    Create New Rules to Old Games One way to keep kids entertained is to have them develop and create new playing rules to the board games you already own. This is a great way for kids to be imaginative, inventive, think outside of the box, work together as a team, communicate and problem solve. Tip s: • Everyone must help come up with the new playing rules and be in agreement. • Document (write down) the new rules. • Must set the rules before gameplay begins. • Do not add additional rules, while the game is being played (unless testing out the new rules and making revisions). • They can create an entirely new game using the pieces from several old games. • Create or add new playing cards. • Make a new game spinner. Some examples: • Monopoly 1) Bid for Start Order -- Going first is a definite advantage because you can buy properties before anyone else gets there. So why shouldn't you have to pay for this advantage? At the start of the game, bid for the first position, then second, etc. In cases where no one wishes to bid, a die roll is used to determine the order. 2) Once Around the Board -- As an alternative to bidding for player order, don't let anyone purchase property until they pass Go once. This will somewhat even out the advantage of going first. 3) Movement Cards -- Give each player a set of cards numbered from 1 to 6. On each roll, a player uses one card and rolls one die. That player then moves the total of both.
    [Show full text]
  • Sosa on Knowledge, Judgment and Guessing
    Sosa on Knowledge, Judgment and Guessing J. Adam Carter Penultimate draft. Forthcoming in Synthese Abstract In Chapter 3 of Judgment and Agency, Ernest Sosa (2015) expli- cates the concept of a fully apt performance. In the course of doing so, he draws from illustrative examples of practical performances and applies lessons drawn to the case of cognitive performances, and in particular, to the cognitive performance of judging. Sosa’s examples in the practical sphere are rich and instructive. But there is, I will argue, an interesting disanalogy between the practical and cognitive examples he relies on. Ultimately, I think the source of the disanalogy is a problematic picture of the cognitive performance of guessing and its connection to knowledge and defeat. Once this critical line of ar- gument is advanced, an alternative picture of guessing, qua cognitive performance, is articulated, one which avoids the problems discussed, and yet remains compatible with Sosa’s broader framework. 1 Introduction The topic of this paper is a particular kind of cognitive performance— guessing. As Sosa (2015) sees it, guessing is like judging, but not quite. Both guessing and judging have an alethic aim. When we guess, as well as when we judge, we aim to get it right. But judgment, on Sosa’s view, does not aim merely to get it right. Judgment has a further epistemic aim, which is to get it right aptly. And getting it right aptly involves competent risk assessment. 1 Competent risk assessment—and not just hitting the relevant target any old way—is obviously important when engaged in sports, such as basketball.
    [Show full text]
  • Matter Guessing Game
    5.5A: Classifying Matter Matter and Energy Matter Guessing Game Project: Materials: Create your own matter - Colored Pencils guessing game! - Index Cards (30) Instructions: 1. Brainstorm: Begin by thinking about how matter is classified. You are going to make your own matter guessing game! This game will be like the party game, Taboo. Begin by making a list of the different forms of matter that you learned about in this lesson. Try to think of at least 30. 2. Label: Now transfer your list to index cards by writing one form of matter at the top of each card. Underneath this title, provide information about the physical properties of each form of matter including: mass, magnetism, physical state, relative density, solubility in water, and electrical conductivity. Here is a sample card: Iron (Fe) - Gray -Metal -Magnetic -Solid -Soft / Ductile -Not Water Soluble -Good Conductor of Heat and Electricity 5.5A: Classifying Matter Matter and Energy Matter Guessing Game Instructions (continued): 3. Decorate: When you are finished with these descriptions, turn your index cards over and draw a question mark on the back of each card. Then use your colored pencils to decorate the background. You can draw whatever you want. Just make sure that your design is consistent from index card to index card so that you will not be able to tell which card is which. 4. Play: Your deck of cards is ready! Begin by dividing your players into two teams. You can play this game with as many people as you can find! Each team will take turns nominating someone from their team to be the ‘giver’.
    [Show full text]
  • GAMES – for JUNIOR OR SENIOR HIGH YOUTH GROUPS Active
    GAMES – FOR JUNIOR OR SENIOR HIGH YOUTH GROUPS Active Games Alka-Seltzer Fizz: Divide into two teams. Have one volunteer on each team lie on his/her back with a Dixie cup in their mouth (bottom part in the mouth so that the opening is facing up). Inside the cup are two alka-seltzers. Have each team stand ten feet away from person on the ground with pitchers of water next to the front. On “go,” each team sends one member at a time with a mouthful of water to the feet of the person lying on the ground. They then spit the water out of their mouths, aiming for the cup. Once they’ve spit all the water they have in their mouth, they run to the end of the line where the next person does the same. The first team to get the alka-seltzer to fizz wins. Ankle Balloon Pop: Give everyone a balloon and a piece of string or yarn. Have them blow up the balloon and tie it to their ankle. Then announce that they are to try to stomp out other people's balloons while keeping their own safe. Last person with a blown up balloon wins. Ask The Sage: A good game for younger teens. Ask several volunteers to agree to be "Wise Sages" for the evening. Ask them to dress up (optional) and wait in several different rooms in your facility. The farther apart the Sages are the better. Next, prepare a sheet for each youth that has questions that only a "Sage" would be able to answer.
    [Show full text]
  • Applied Epistemology and Understanding in Information Studies
    PUBLISHED QUARTERLY BY THE UNIVERSITY OF BORÅS, SWEDEN VOL. 22 NO. 4, DECEMBER, 2017 Contents | Author index | Subject index | Search | Home Applied epistemology and understanding in information studies Tim Gorichanaz Introduction. Applied epistemology allows information studies to benefit from developments in philosophy. In information studies, epistemic concepts are rarely considered in detail. This paper offers a review of several epistemic concepts, focusing on understanding, as a call for further work in applied epistemology in information studies. Method. A hermeneutic literature review was conducted on epistemic concepts in information studies and philosophy. Relevant research was retrieved and reviewed iteratively as the research area was refined. Analysis. A conceptual analysis was conducted to determine the nature and relationships of the concepts surveyed, with an eye toward synthesizing conceptualizations of understanding and opening future research directions. Results. The epistemic aim of understanding is emerging as a key research frontier for information studies. Two modes of understanding (hermeneutic and epistemological) were brought into a common framework. Conclusions. Research on the concept of understanding in information studies will further naturalistic information research and provide coherence to several strands of philosophic thought. What is information studies for? Presumably, the products and processes that result from information research are intended for some purpose. Information involves intellectual activity, and so it would seem that information products and processes contribute to some epistemic aims (i.e., goals related to knowing), among other possible aims. These aims are generally left implicit; explicating them, however, can clarify the contribution of a given study, product or service. It seems that information studies has long assumed knowledge as its default epistemic aim; understanding has emerged as an intriguing alternative in recent years, necessitating reconsideration of epistemic frameworks.
    [Show full text]
  • Sneak It In! Gotta Go Fast Virtual Scattergories “A Twist of Charades”
    Virtual Happy Hour Games Sneak It In! The group gets divided into smaller teams through breakout rooms. Depending on the size of the original group, you could split up into 2-6 teams. From there each team has to come up with a word or phrase that they need to sneak into the original group conversation without any of the other teams guessing what their word/phrase is. After a few minutes of brainstorming individually, each group comes back together as one. The goal is to incorporate your team’s word/phrase into the conversation as many times as possible without the other teams figuring out what your word/phrase is. The team who sneaks it in the most amount of times or doesn’t get caught by the end of the happy hour wins the game! Gotta Go Fast This game will be an indoor scavenger hunt. A host will call out a name of a common household object and the first participant who runs to collect the item, bring it back to show it on screen, and type the name of the item in the chat box will win that round. This is a good game to get people moving around out of their seat and laughing! Virtual Scattergories Similar to the popular board game, there is a list of items everyone needs to think and write on their sheet of paper. The answers must start with the same letter that is established at the beginning of each round. What makes this unique is companies and groups can create their own lists and have fun with their coworkers/friends! If people are doing this with their friends, they can create lists with many inside jokes and have a lot of laughs! “A Twist of Charades” We’re taking charades to a new level by reversing it! In this version, everyone in the group will act out the word on the selected card while a single person in the group tries to guess the word.
    [Show full text]
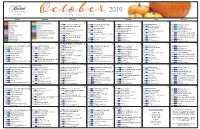
  • Activities Calendar
    2019 ACTIVITIES CALENDAR Sunday Monday Tuesday Wednesday Thursday Friday Saturday 1 2 3 4 5 10:00 B Resistance Weight Exercise (A) 10:00 B Communion & Prayers (A) 10:00 B Balloon Volleyball (C) 9:00 LI Shabbat Services 10:00 B Morning Cardio (C) 10:00 B Chair Yoga w/ Janice (C) 10:30 BT Banks and Post Office (M) 10:15 B Muscle Hustle (A) 11:00 B Exercise w/ Michael Levenson 11:00 B Big Boggle (C) 10:00 BT Riverhead Outlets (M) 10:30 B Word Scramble (A) 10:30 BT Stop and Shop (G) 11:00 CK Women’s Group (C) 10:00 B Tone & Burn (C) 11:00 LI Resident-Run Rosary 11:15 C The Worldly Traveler: Venice (A) 11:15 B Big Boggle (A) 2:00 C Afternoon Matinee 11:00 C Series Showcase: Father Brown 2:00 C Saturday Matinee 2:00 C Cinema Matinee 2:00 BT Marshals (M) 2:00 C Cinema Matinee 11:15 B Anagrams (C) 2:00 BT CVS (M) 2:15 AR Fall Wreath Workshop (CA) 2:15 B Round Circle Sing Along (P) 2:15 B Supreme Court Mock Proceeding 2:00 C Cinema Matinee B B 3:00 B Loaded Questions Social (C) 2:15 Tin Lizzie Ford Motor Q & A (C) (C) 2:15 Taboo (C) 2:15 B Wacky Wordies (C) 3:00 B Piano Social w/ J.K. Hodge 3:00 B Hoop Shot Social (C) 3:00 B Skeeball Social (C) 3:00 B Horse Racing Social (C) 3:15 AR Fall Jewelry Workshop (S) 4:00 BR Bingo (C) 4:00 BR Bingo (C) 4:00 BR Bingo (C) 4:00 BR Bingo (C) 4:00 BR Bingo (C) 7:00 B Improve Comedy Night (P) 7:00 B On Broadway (C) 7:00 B Team Game: Trouble (C) 7:00 B Heads Up! Guessing Game (C) 7:00 B Trivial Pursuit (C) 6 7 Yom Kippur Begins at Sundown 8 9 10 11 12 8:30 BT Mass at St.
    [Show full text]