A Transformational Approach to Jazz Harmony
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Harmony Crib Sheets
Jazz Harmony Primer General stuff There are two main types of harmony found in modern Western music: 1) Modal 2) Functional Modal harmony generally involves a static drone, riff or chord over which you have melodies with notes chosen from various scales. It’s common in rock, modern jazz and electronic dance music. It predates functional harmony, too. In some types of modal music – for example in jazz - you get different modes/chord scale sounds over the course of a piece. Chords and melodies can be drawn from these scales. This kind of harmony is suited to the guitar due to its open strings and retuning possibilities. We see the guitar take over as a songwriting instrument at about the same time as the modes become popular in pop music. Loop based music also encourages this kind of harmony. It has become very common in all areas of music since the late 20th century under the influence of rock and folk music, composers like Steve Reich, modal jazz pioneered by Miles Davis and John Coltrane, and influences from India, the Middle East and pre-classical Western music. Functional harmony is a development of the kind of harmony used by Bach and Mozart. Jazz up to around 1960 was primarily based on this kind of harmony, and jazz improvisation was concerned with the improvising over songs written by the classically trained songwriters and film composers of the era. These composers all played the piano, so in a sense functional harmony is piano harmony. It’s not really guitar shaped. When I talk about functional harmony I’ll mostly be talking about ways we can improvise and compose on pre-existing jazz standards rather than making up new progressions. -

Riemann's Functional Framework for Extended Jazz Harmony James
Riemann’s Functional Framework for Extended Jazz Harmony James McGowan The I or tonic chord is the only chord which gives the feeling of complete rest or relaxation. Since the I chord acts as the point of rest there is generated in the other chords a feeling of tension or restlessness. The other chords therefore must 1 eventually return to the tonic chord if a feeling of relaxation is desired. Invoking several musical metaphors, Ricigliano’s comment could apply equally well to the tension and release of any tonal music, not only jazz. Indeed, such metaphors serve as essential points of departure for some extended treatises in music theory.2 Andrew Jaffe further associates “tonic,” “stability,” and “consonance,” when he states: “Two terms used to refer to the extremes of harmonic stability and instability within an individual chord or a chord progression are dissonance and consonance.”3 One should acknowledge, however, that to the non-jazz reader, reference to “tonic chord” implicitly means triad. This is not the case for Ricigliano, Jaffe, or numerous other writers of pedagogical jazz theory.4 Rather, in complete indifference to, ignorance of, or reaction against the common-practice principle that only triads or 1 Ricigliano 1967, 21. 2 A prime example, Berry applies the metaphor of “motion” to explore “Formal processes and element-actions of growth and decline” within different musical domains, in diverse stylistic contexts. Berry 1976, 6 (also see 111–2). An important precedent for Berry’s work in the metaphoric dynamism of harmony and other parameters is found in the writings of Kurth – particularly in his conceptions of “sensuous” and “energetic” harmony. -
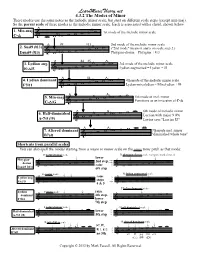
View Printable PDF of 4.2 the Modes of Minor
LearnMusicTheory.net 4.3.2 The Modes of Minor These modes use the same notes as the melodic minor scale, but start on different scale steps (except min-maj). So the parent scale of these modes is the melodic minor scale. Each is associated with a chord, shown below. 1. Min-maj 1st mode of the melodic minor scale C- w wmw ^ & w wmbw w w b9 §13 2nd mode of the melodic minor scale 2. Susb9 (§13) wmw w ("2nd mode" means it starts on scale step 2.) Dsusb9 (§13) & wmbw w w w Phrygian-dorian = Phyrgian + §13 #4 #5 3. Lydian aug. mbw 3rd mode of the melodic minor scale wmw w Lydian augmented = Lydian + #5 Eb ^ #5 & bw w w w #4 4. Lydian dominant 4th mode of the melodic minor scale w wmbw w F7#11 & w w w wm Lydian-mixolydian = Mixolydian + #4 5. Min-maj w w 5th mode of mel. minor wmw wmbw Functions as an inversion of C- C- ^ /G & w w ^ 6th mode of melodic minor 6. Half-diminished w w m w wmbw w Locrian with major 9 (§9) A-7b5 (§9) & w w Levine says "Locrian #2" w 7. Altered dominant wmbw w w w 7th mode mel. minor B7alt & wm w "diminished whole tone" Shortcuts from parallel scales You can also spell the modes starting from a major or minor scale on the same tonic pitch as that mode: D natural minor scale D phrygian-dorian scale (compare marked notes) lower Phrygian- I I 2nd step, I I dorian w bw w w raise _ w nw w w Dsusb9 (§13) & w w w _ & bw w w w 6th step _ w Eb major scale Eb lydian augmented scale Lydian aug. -

Jazz Lines Publications Fall Catalog 2009
Jazz lines PubLications faLL CataLog 2009 Vocal and Instrumental Big Band and Small Group Arrangements from Original Manuscripts & Accurate Transcriptions Jazz Lines Publications PO Box 1236 Saratoga Springs NY 12866 USA www.ejazzlines.com [email protected] 518-587-1102 518-587-2325 (Fax) KEY: I=Instrumental; FV=Female Vocal; MV=Male Vocal; FVQ=Female Vocal Quartet; FVT= Femal Vocal Trio PERFORMER / TITLE CAT # DESCRIPTION STYLE PRICE FORMAT ARRANGER Here is the extended version of I've Got a Gal in Kalamazoo, made famous by the Glenn Miller Orchestra in the film Orchestra Wives. This chart differs significantly from the studio recorded version, and has a full chorus band intro, an interlude leading to the vocals, an extra band bridge into a vocal reprise, plus an added 24 bar band section to close. At five and a half minutes long, it's a (I'VE GOT A GAL IN) VOCAL / SWING - LL-2100 showstopper. The arrangement is scored for male vocalist plus a backing group of 5 - ideally girl, 3 tenors and baritone, and in the GLENN MILLER $ 65.00 MV/FVQ DIFF KALAMAZOO Saxes Alto 2 and Tenor 1 both double Clarinets. The Tenor solo is written on the 2nd Tenor part and also cross-cued on the male vocal part. The vocal whistling in the interlude is cued on the piano part, and we have written out the opening Trumpet solo in full. Trumpets 1-4: Eb6, Bb5, Bb5, Bb5; Trombones 1-4: Bb4, Ab4, Ab4, F4; Male Vocal: Db3 - Db4 (8 steps): Vocal key: Db to Gb. -

Cds by Composer/Performer
CPCC MUSIC LIBRARY COMPACT DISCS Updated May 2007 Abercrombie, John (Furs on Ice and 9 other selections) guitar, bass, & synthesizer 1033 Academy for Ancient Music Berlin Works of Telemann, Blavet Geminiani 1226 Adams, John Short Ride, Chairman Dances, Harmonium (Andriessen) 876, 876A Adventures of Baron Munchausen (music composed and conducted by Michael Kamen) 1244 Adderley, Cannonball Somethin’ Else (Autumn Leaves; Love For Sale; Somethin’ Else; One for Daddy-O; Dancing in the Dark; Alison’s Uncle 1538 Aebersold, Jamey: Favorite Standards (vol 22) 1279 pt. 1 Aebersold, Jamey: Favorite Standards (vol 22) 1279 pt. 2 Aebersold, Jamey: Gettin’ It Together (vol 21) 1272 pt. 1 Aebersold, Jamey: Gettin’ It Together (vol 21) 1272 pt. 2 Aebersold, Jamey: Jazz Improvisation (vol 1) 1270 Aebersold, Jamey: Major and Minor (vol 24) 1281 pt. 1 Aebersold, Jamey: Major and Minor (vol 24) 1281 pt. 2 Aebersold, Jamey: One Dozen Standards (vol 23) 1280 pt. 1 Aebersold, Jamey: One Dozen Standards (vol 23) 1280 pt. 2 Aebersold, Jamey: The II-V7-1 Progression (vol 3) 1271 Aerosmith Get a Grip 1402 Airs d’Operettes Misc. arias (Barbara Hendricks; Philharmonia Orch./Foster) 928 Airwaves: Heritage of America Band, U.S. Air Force/Captain Larry H. Lang, cond. 1698 Albeniz, Echoes of Spain: Suite Espanola, Op.47 and misc. pieces (John Williams, guitar) 962 Albinoni, Tomaso (also Pachelbel, Vivaldi, Bach, Purcell) 1212 Albinoni, Tomaso Adagio in G Minor (also Pachelbel: Canon; Zipoli: Elevazione for Cello, Oboe; Gluck: Dance of the Furies, Dance of the Blessed Spirits, Interlude; Boyce: Symphony No. 4 in F Major; Purcell: The Indian Queen- Trumpet Overture)(Consort of London; R,Clark) 1569 Albinoni, Tomaso Concerto Pour 2 Trompettes in C; Concerto in C (Lionel Andre, trumpet) (also works by Tartini; Vivaldi; Maurice André, trumpet) 1520 Alderete, Ignacio: Harpe indienne et orgue 1019 Aloft: Heritage of America Band (United States Air Force/Captain Larry H. -

Sendung, Sendedatum
WDR 3 Jazz & World, 24. Februar 2018 Persönlich mit Götz Alsmann 13:04-15:00 Stand: 23. Februar 2018 E-Mail: [email protected] WDR JazzRadio: http://jazz.wdr.de Moderation: Götz Alsmann Redaktion: Bernd Hoffmann 22:04-24:00 Laufplan 1. Tempo’s Tempo K/T: Nino Tempo 2:33 NINO TEMPO NCB 1050 LP: The Girl Can’t Help It 2. Sweet And Lovely K/T: Gus Arnheim/ Nappy Lemare 4:25 COLEMAN HAWKINS Pablo 2310890; LC: 03254 LP: Jazz Dance 3. Why Was I Born K/T: Jerome Kern/ Oscar Hammerstein 8:25 GENE AMMONS & Verve 2578; LC: 00383 SONNY STITT LP: Boss Tenors In Orbit 4. Wheel of Fortune K/T: Benny Benjamin/ George Davis Weiss 2:50 THE FOUR FLAMES Specialty 423 Single 5. Le Papillon K/T: Edvard Grieg 2:57 CLAUDE THORNHILL Circle 19 CD: Claude Thornhill 1941 & 1947 6. Träumerei K/T: Robert Schumann 2:12 CLAUDE THORNHILL wie Titel 5 7. Robbins’ Nest K/T: Sir Charles Thompson 3:59 CLAUDE THRONHILL Hindsight 108; LC: 00171 LP: The Uncollected Claude Thornhill 1947 8. Just About This Time K/T: LouisPrima/ PaulCunningham/ 3:59 Last Night Sidney Miller CLAUDE THORNHILL wie Titel 7 9. Love Me Love K/T: Wolfe /Lee 2:30 FRAN WARREN MGM 3394; LC: 00383 LP: Mood Indigo 10. Donna Lee K/T: Charlie Parker 2:27 CLAUDE THORNHILL wie Titel 7 11. Penthouse Serenade K/T: Val Burton/ Will Jason 2:45 HELEN O’CONNELL Hindsight 228; LC: 00171 LP: The Uncollected Helen O’Connell 1953 Dieses Manuskript ist ausschließlich zum persönlichen, privaten Gebrauch bestimmt. -

Charles Ruggiero's "Tenor Attitudes": an Analytical Approach to Jazz
Louisiana State University LSU Digital Commons LSU Doctoral Dissertations Graduate School 2016 Charles Ruggiero's "Tenor Attitudes": An Analytical Approach to Jazz Styles and Influences Nicholas Vincent DiSalvio Louisiana State University and Agricultural and Mechanical College, [email protected] Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_dissertations Part of the Music Commons Recommended Citation DiSalvio, Nicholas Vincent, "Charles Ruggiero's "Tenor Attitudes": An Analytical Approach to Jazz Styles and Influences" (2016). LSU Doctoral Dissertations. 1. https://digitalcommons.lsu.edu/gradschool_dissertations/1 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Doctoral Dissertations by an authorized graduate school editor of LSU Digital Commons. For more information, please [email protected]. CHARLES RUGGIERO’S “TENOR ATTITUDES”: AN ANALYTICAL APPROACH TO JAZZ STYLES AND INFLUENCES A Written Document Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for the degree of Doctor of Musical Arts in The School of Music by Nicholas Vincent DiSalvio B.M., Rowan University, 2009 M.M., Illinois State University, 2013 May 2016 For my wife Pagean: without you, I could not be where I am today. ii ACKNOWLEDGEMENTS I would first like to thank my committee for their patience, wisdom, and guidance throughout the writing and revising of this document. I extend my heartfelt thanks to Dr. Griffin Campbell and Dr. Willis Delony for their tireless work with and belief in me over the past three years, as well as past professors Dr. -

Allan Holdsworth Schille Reshaping Harmony
BJØRN ALLAN HOLDSWORTH SCHILLE RESHAPING HARMONY Master Thesis in Musicology - February 2011 Institute of Musicology| University of Oslo 3001 2 2 Acknowledgment Writing this master thesis has been an incredible rewarding process, and I would like to use this opportunity to express my deepest gratitude to those who have assisted me in my work. Most importantly I would like to thank my wonderful supervisors, Odd Skårberg and Eckhard Baur, for their good advice and guidance. Their continued encouragement and confidence in my work has been a source of strength and motivation throughout these last few years. My thanks to Steve Hunt for his transcription of the chord changes to “Pud Wud” and helpful information regarding his experience of playing with Allan Holdsworth. I also wish to thank Jeremy Poparad for generously providing me with the chord changes to “The Sixteen Men of Tain”. Furthermore I would like to thank Gaute Hellås for his incredible effort of reviewing the text and providing helpful comments where my spelling or formulations was off. His hard work was beyond what any friend could ask for. (I owe you one!) Big thanks to friends and family: Your love, support and patience through the years has always been, and will always be, a source of strength. And finally I wish to acknowledge Arne Torvik for introducing me to the music of Allan Holdsworth so many years ago in a practicing room at the Grieg Academy of Music in Bergen. Looking back, it is obvious that this was one of those life-changing moments; a moment I am sincerely grateful for. -

From King Records Month 2018
King Records Month 2018 = Unedited Tweets from Zero to 180 Aug. 3, 2018 Zero to 180 is honored to be part of this year's celebration of 75 Years of King Records in Cincinnati and will once again be tweeting fun facts and little known stories about King Records throughout King Records Month in September. Zero to 180 would like to kick off things early with a tribute to King session drummer Philip Paul (who you've heard on Freddy King's "Hideaway") that is PACKED with streaming audio links, images of 45s & LPs from around the world, auction prices, Billboard chart listings and tons of cool history culled from all the important music historians who have written about King Records: “Philip Paul: The Pulse of King” https://www.zeroto180.org/?p=32149 Aug. 22, 2018 King Records Month is just around the corner - get ready! Zero to 180 will be posting a new King history piece every 3 days during September as well as October. There will also be tweeting lots of cool King trivia on behalf of Xavier University's 'King Studios' historic preservation collaborative - a music history explosion that continues with this baseball-themed celebration of a novelty hit that dominated the year 1951: LINK to “Chew Tobacco Rag” Done R&B (by Lucky Millinder Orchestra) https://www.zeroto180.org/?p=27158 Aug. 24, 2018 King Records helped pioneer the practice of producing R&B versions of country hits and vice versa - "Chew Tobacco Rag" (1951) and "Why Don't You Haul Off and Love Me" (1949) being two examples of such 'crossover' marketing. -

Harmonic Expectation in Twelve-Bar Blues Progressions Bryn Hughes
Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2011 Harmonic Expectation in Twelve-Bar Blues Progressions Bryn Hughes Follow this and additional works at the FSU Digital Library. For more information, please contact [email protected] THE FLORIDA STATE UNIVERSITY COLLEGE OF MUSIC HARMONIC EXPECTATION IN TWELVE-BAR BLUES PROGRESSIONS By BRYN HUGHES A dissertation submitted to the College of Music in partial fulfillment of the requirements for the degree of Doctor of Philosophy Degree Awarded: Summer Semester, 2011 The members of the committee approve the dissertation of Bryn Hughes defended on July 1, 2011. ___________________________________ Nancy Rogers Professor Directing Dissertation ___________________________________ Denise Von Glahn University Representative ___________________________________ Matthew Shaftel Committee Member ___________________________________ Clifton Callender Committee Member Approved: _____________________________________ Evan Jones, Chair, Department of Music Theory and Composition _____________________________________ Don Gibson, Dean, College of Music The Graduate School has verified and approved the above-named committee members. ii To my father, Robert David Moyse, for teaching me about the blues, and to the love of my life, Jillian Bracken. Thanks for believing in me. iii ACKNOWLEDGEMENTS Before thanking anyone in particular, I would like to express my praise for the Florida State University music theory program. The students and faculty provided me with the perfect combination of guidance, enthusiasm, and support to allow me to succeed. My outlook on the field of music theory and on academic life in general was profoundly shaped by my time as a student at FSU. I would like to express my thanks to Richard Parks and Catherine Nolan, both of whom I studied under during my time as a student at the University of Western Ontario and inspired and motivated me to make music theory a career. -

The Evolution of Ornette Coleman's Music And
DANCING IN HIS HEAD: THE EVOLUTION OF ORNETTE COLEMAN’S MUSIC AND COMPOSITIONAL PHILOSOPHY by Nathan A. Frink B.A. Nazareth College of Rochester, 2009 M.A. University of Pittsburgh, 2012 Submitted to the Graduate Faculty of The Kenneth P. Dietrich School of Arts and Sciences in partial fulfillment of the requirements for the degree of Doctor of Philosophy University of Pittsburgh 2016 UNIVERSITY OF PITTSBURGH THE KENNETH P. DIETRICH SCHOOL OF ARTS AND SCIENCES This dissertation was presented by Nathan A. Frink It was defended on November 16, 2015 and approved by Lawrence Glasco, PhD, Professor, History Adriana Helbig, PhD, Associate Professor, Music Matthew Rosenblum, PhD, Professor, Music Dissertation Advisor: Eric Moe, PhD, Professor, Music ii DANCING IN HIS HEAD: THE EVOLUTION OF ORNETTE COLEMAN’S MUSIC AND COMPOSITIONAL PHILOSOPHY Nathan A. Frink, PhD University of Pittsburgh, 2016 Copyright © by Nathan A. Frink 2016 iii DANCING IN HIS HEAD: THE EVOLUTION OF ORNETTE COLEMAN’S MUSIC AND COMPOSITIONAL PHILOSOPHY Nathan A. Frink, PhD University of Pittsburgh, 2016 Ornette Coleman (1930-2015) is frequently referred to as not only a great visionary in jazz music but as also the father of the jazz avant-garde movement. As such, his work has been a topic of discussion for nearly five decades among jazz theorists, musicians, scholars and aficionados. While this music was once controversial and divisive, it eventually found a wealth of supporters within the artistic community and has been incorporated into the jazz narrative and canon. Coleman’s musical practices found their greatest acceptance among the following generations of improvisers who embraced the message of “free jazz” as a natural evolution in style. -

Jazzflits 01 09 2003 - 01 09 2021
1 19de JAARGANG, NR. 361 16 AUGUSTUS 2021 IN DIT NUMMER: 1 BERICHTEN 5 JAZZ OP DE PLAAT Eve Beuvens, Steve Cole, Flat Earth Society Orchestra, Ben van de Dungen, Gerry Gibbs e.a. EN VERDER (ONDER MEER): 10 Lee Morgan (Erik Marcel Frans) 16 Europe Jazz Media Chart Augustus 18 J AAR JAZZFLITS 01 09 2003 - 01 09 2021 NR. 362 KOMT 13 SEPT. UIT ONAFHANKELIJK JAZZPERIODIEK SINDS 2003 BERICHTEN CORONA-EDITIE FESTIVAL GENT JAZZ TREKT 20.000 BEZOEKERS In de tien dagen dat Gent Jazz ‘Back to Live’ duurde (van 9 tot en met 18 juli), passeerden zo’n twintigdui- zend mensen de festivalkassa. Van- wege de coronacrisis was op het laatste moment een speciale editie van het jaarlijkse zomerfestival in elkaar gezet met veel Belgische mu- sici. Maar ook de pianisten Monty Alexander, Tigran Hamasyan en ac- cordeonist Richard Galliano kwamen naar Gent. Festivaldirecteur Ber- trand Flamang sprak na afloop van een succesvol evenement. Cassandra Wilson tijdens het North Sea Jazz Festival 2015. (Foto: Joke Schot) Flamang: “In mei leek het er nog op dat deze editie niet zou doorgaan. Maar op CASSANDRA WILSON, STANLEY CLARKE twee maanden tijd zijn we erin geslaagd EN BILLY HART BENOEMD TOT NEA JAZZ MASTER om een coronaveilig evenement op po- ten te zetten.” Bezoekers konden zich Drummer Billy Hart, Bassist Stanley Clarke en zangeres niet vrij bewegen. Ze zaten per bubbel Cassandra Wilson zijn Benoemd tot NEA Jazz Master aan stoelen en tafels onder een giganti- 2022. Saxofonist Donald Harrison ontvangt de A.B. Spell- man NEA Jazz Masters Fellowship for Jazz Advocacy.