DOCSLIB.ORG

Asymmetric Transmitter Binding Sites of Fetal Muscle Acetylcholine Receptors Shape Their Synaptic Response

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Asymmetric Transmitter Binding Sites of Fetal Muscle Acetylcholine Receptors Shape Their Synaptic Response Asymmetric transmitter binding sites of fetal muscle acetylcholine receptors shape their synaptic response Tapan K. Nayak and Anthony Auerbach1 Department of Physiology and Biophysics, State University of New York, Buffalo, NY 14214 Edited by Jean-Pierre Changeux, Institut Pasteur, Paris, France, and approved July 3, 2013 (received for review May 1, 2013) Neuromuscular acetylcholine receptors (AChRs) have two trans- sites are functionally equivalent, but in the fetal subtype, the α−γ mitter binding sites: at α−δ and either α−γ (fetal) or α–e (adult) site has a higher affinity for ACh and provides more energy for subunit interfaces. The γ-subunit of fetal AChRs is indispensable gating than α−δ/e. Simulations of end plate currents suggest the for the proper development of neuromuscular synapses. We esti- differences in activation properties between e- and γ-AChR that mated parameters for acetylcholine (ACh) binding and gating from may impact synaptic development. single channel currents of fetal mouse AChRs expressed in tissue- cultured cells. The unliganded gating equilibrium constant is smaller Results and less voltage-dependent than in adult AChRs. However, the Definitions and Models. AChRs undergo a global, reversible allo- α−γ binding site has a higher affinity for ACh and provides more steric transition between closed (C) and open channel (O) states. binding energy for gating compared with α−e; therefore, the dili- This complex reaction includes numerous changes in structure ganded gating equilibrium constant at −100 mV is comparable for and dynamics at the binding sites (that set the affinity for ago- both receptor subtypes. The −2.2 kcal/mol extra binding energy nist), side chains and domains throughout the protein (that set from α−γ compared with α−δ and α−e is accompanied by a higher the equilibrium constant), and narrow regions of the pore (that resting affinity for ACh, mainly because of slower transmitter dis- set the ionic conductance). We use “gating” to refer to every- sociation. End plate current simulations suggest that the higher thing that happens in C↔O, either with or without agonists at affinity and increased energy from α−γ are essential for generat- the binding sites. Agonist binding to AChRs is also a complex ing synaptic responses at low pulse [ACh]. reaction that requires both diffusion of the ligand and a change in protein conformation (23). We use “binding” to refer to ev- allostery | cholinergic | nicotinic | kinetics erything that happens in the formation of a liganded complex. The binding and gating energies reported below are the sums of the energy changes for all of the microscopic steps within each of ertebrate neuromuscular acetylcholine receptors (AChRs) these multifaceted processes. are ligand-gated ion channels comprised of five subunits: two V The model used for estimating the parameters is shown in α(1) and one each of β, δ, and either γ or e. In most species, the Fig. 1A. The free energy difference, O vs. C, is ΔG , where n is γ-subunit is replaced by e during postnatal development. Elec- n trical activity in muscle cells induced by the neurotransmitter the number of bound agonists (A). The horizontal arrows rep- resent ligand binding at two sites. The free energy for binding to acetylcholine (ACh) is important for the molecular maturation fi Δ α−γ e α−δ γ e the lower-af nity C state is GLA (either / or ) and the of -to -AChRs (1, 2). fi Δ Δ γ higher-af nity O state is GHA. GB is the net binding free Without -subunit, neuromuscular synapses do not develop Δ = Δ − Δ ΔΔ properly (3) and are abnormal in innervation patterns (4) and energy from each ligand ( GB GHA GLA; really a G). muscle fiber-type composition (5). In mice, the γ-subunit KO is From detailed balance, lethal (6), and in humans, mutations in the cholinergic receptor, Δ = Δ + Δ + Δ : [1] nicotinic, gamma (CHRNG) gene that encodes for γ-subunit are G2 G0 GB1 GB2 associated with lethal forms of multiple pterygium and Escobar – The gating energy with two bound agonists is equal to the in- syndromes (7 9). fi AChRs have two transmitter binding sites located in the ex- trinsic gating energy plus the binding energy from two af nity Δ tracellular domain at α–δ and α–γ/e-subunit interfaces. In adult changes. GB is proportional to the log of the coupling constant Δ AChRs, the α−δ and α−e sites are equal and independent insofar (the C vs. O equilibrium dissociation constant ratio), and G0 is as each has the same affinity for ACh and supplies the same proportional to the log of the allosteric constant (the gating Δ amount of binding energy for gating (10). In fetal AChRs, the equilibrium constant in the absence of agonists). GB is the free fi two binding sites are asymmetric with regard to agonist affinity, energy generated by the af nity change for the agonist at each with estimates for the ratio of resting equilibrium dissociation transmitter binding site that ultimately contributes to the in- constants for ACh ranging from ∼5- (11, 12) to >100-fold (13, creased relative stability of A2O vs. A2C. We estimated binding 14). γ-AChRs also have a longer open channel lifetime, a smaller and gating rate constants from single channel interval durations, + unitary conductance, and a lower Ca2 permeability than equilibrium constants from the rate constant ratios, and energies e-AChRs (15–17). by taking the log of the equilibrium constants [ΔG = −0.59 Fetal AChRs hold a special place in the history of ion channel lnKeq (kcal/mol)]. biophysics. The first single channel recordings from cells were of ΔGWT fi γ-AChRs (18). They were also the first ion channels to be ana- 0 . Our rst step was to estimate the energy difference be- lyzed according to a thermodynamic cycle, which required quan- tween C and O with only water present at the two transmitter tifying constitutive activity in the absence of agonists (19). These pioneering studies of single channel currents from mouse myo- tubes led to the estimate that the unliganded gating equilibrium Author contributions: T.K.N. and A.A. designed research; T.K.N. performed research; T.K.N. − constant of γ-AChRs is ∼1.6 × 10 6. γ-AChRs were also the first and A.A. analyzed data; and T.K.N. and A.A. wrote the paper. channels for which the rate and equilibrium constants for closed The authors declare no conflict of interest. channel binding and liganded gating were measured (13, 20–22). This article is a PNAS Direct Submission. We have used improved methods of analysis to extend these 1To whom correspondence should be addressed. E-mail: [email protected]. γ studies of -AChRs with regard to both the rate constants and This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10. thermodynamics of activation. In adult AChRs, the two binding 1073/pnas.1308247110/-/DCSupplemental. 13654–13659 | PNAS | August 13, 2013 | vol. 110 | no. 33 www.pnas.org/cgi/doi/10.1073/pnas.1308247110 Downloaded by guest on October 1, 2021 is +10.5 kcal/mol. Some but not all of the offset in the γ- vs. e-lines in Fig. 2B can be attributed to different voltage sensitiv- ities of the two subtypes. Fig. 2C shows constitutive activity of WT γ-AChRs measured in the absence of agonists at −100 mV. From the distribution of WT = ; ± −1 open interval durations, b0 2 546 635 s (mean open time ∼ μ WT 400 s). E0 is the ratio of the forward/backward gating rate WT = : × −4 −1 constants, and therefore, we calculate that f0 1 32 10 s (each unliganded γ-AChR opens spontaneously about 11 times/d). For comparison, the gating rate constants at −100 mV in e-AChRs Fig. 1. Models and mutations. (A) Front plane is a thermodynamic cycle for WT = × −4 −1 ∼ WT = ; −1 one binding site. Thick lines are the physiological two-site scheme. (B) Side are f0 67 10 s ( 600 times/d) and b0 8 800 s chain substitutions at homologous positions in e- and γ-AChRs are equiva- (meanopentime∼ 110 μs) (Table 2). The γ→e-subunit sub- lent. Plot of ΔΔG2 (kcal/mol) in fetal vs. adult AChRs for 11 different point stitution increases both the forward and backward gating rate mutations (open, choline; filled, ACh). Locations of the residues are shown in constants but to different extents; therefore, the unliganded Fig. S1A. Slope of the regression = 0.93 ± 0.04 (R2 = 0.98). gating equilibrium constant is also increased. ACh ACh ΔG2 and ΔGB . We next measured the total energy from the fi Δ WT binding sites. It is dif cult to estimate G0 directly, because affinity changes for ACh at both the α−δ and α−γ binding sites. without agonists, WT γ-AChRs rarely open. However, by using Δ ACh Our approach was to measure G2 , and then, armed with combinations of background mutations that increase constitutive knowledge to ΔGWT, we calculate ðΔGACh + ΔGAChÞ using Eq. 1. Δ WT 0 B1 B2 activity, it is possible to estimate G0 by extrapolation (24, 25). At high [ACh], intracluster activity reflects mainly A C↔A O Δ 2 2 If the only effect of each mutation is to make G0 less positive gating. To facilitate gating rate constant measurements, we (more favorable for opening) and if each mutation acts inde- depolarized the membrane to +70 mV (to reduce channel block Δ WT pendently, then G0 can be estimated from measurements of by the agonist) and added background mutations that increased ΔΔ ACh ACh their effects on the energy of diliganded gating ( G2).
Load more

Recommended publications
  • Familial Cortical Myoclonus Caused by Mutation in NOL3 by Jonathan Foster Rnsseil DISSERTATION Submitted in Partial Satisfaction
    Familial Cortical Myoclonus Caused by Mutation in NOL3 by Jonathan Foster Rnsseil DISSERTATION Submitted in partial satisfaction of the requirements for the degree of DOCTOR OF PHILOSOPHY in Biomedical Sciences in the Copyright 2013 by Jonathan Foster Russell ii I dedicate this dissertation to Mom and Dad, for their adamantine love and support iii No man has earned the right to intellectual ambition until he has learned to lay his course by a star which he has never seen—to dig by the divining rod for springs which he may never reach. In saying this, I point to that which will make your study heroic. For I say to you in all sadness of conviction, that to think great thoughts you must be heroes as well as idealists. Only when you have worked alone – when you have felt around you a black gulf of solitude more isolating than that which surrounds the dying man, and in hope and in despair have trusted to your own unshaken will – then only will you have achieved. Thus only can you gain the secret isolated joy of the thinker, who knows that, a hundred years after he is dead and forgotten, men who never heard of him will be moving to the measure of his thought—the subtile rapture of a postponed power, which the world knows not because it has no external trappings, but which to his prophetic vision is more real than that which commands an army. -Oliver Wendell Holmes, Jr. iv ACKNOWLEDGMENTS I am humbled by the efforts of many, many others who were essential for this work.
    [Show full text]
  • Ion Channels
    UC Davis UC Davis Previously Published Works Title THE CONCISE GUIDE TO PHARMACOLOGY 2019/20: Ion channels. Permalink https://escholarship.org/uc/item/1442g5hg Journal British journal of pharmacology, 176 Suppl 1(S1) ISSN 0007-1188 Authors Alexander, Stephen PH Mathie, Alistair Peters, John A et al. Publication Date 2019-12-01 DOI 10.1111/bph.14749 License https://creativecommons.org/licenses/by/4.0/ 4.0 Peer reviewed eScholarship.org Powered by the California Digital Library University of California S.P.H. Alexander et al. The Concise Guide to PHARMACOLOGY 2019/20: Ion channels. British Journal of Pharmacology (2019) 176, S142–S228 THE CONCISE GUIDE TO PHARMACOLOGY 2019/20: Ion channels Stephen PH Alexander1 , Alistair Mathie2 ,JohnAPeters3 , Emma L Veale2 , Jörg Striessnig4 , Eamonn Kelly5, Jane F Armstrong6 , Elena Faccenda6 ,SimonDHarding6 ,AdamJPawson6 , Joanna L Sharman6 , Christopher Southan6 , Jamie A Davies6 and CGTP Collaborators 1School of Life Sciences, University of Nottingham Medical School, Nottingham, NG7 2UH, UK 2Medway School of Pharmacy, The Universities of Greenwich and Kent at Medway, Anson Building, Central Avenue, Chatham Maritime, Chatham, Kent, ME4 4TB, UK 3Neuroscience Division, Medical Education Institute, Ninewells Hospital and Medical School, University of Dundee, Dundee, DD1 9SY, UK 4Pharmacology and Toxicology, Institute of Pharmacy, University of Innsbruck, A-6020 Innsbruck, Austria 5School of Physiology, Pharmacology and Neuroscience, University of Bristol, Bristol, BS8 1TD, UK 6Centre for Discovery Brain Science, University of Edinburgh, Edinburgh, EH8 9XD, UK Abstract The Concise Guide to PHARMACOLOGY 2019/20 is the fourth in this series of biennial publications. The Concise Guide provides concise overviews of the key properties of nearly 1800 human drug targets with an emphasis on selective pharmacology (where available), plus links to the open access knowledgebase source of drug targets and their ligands (www.guidetopharmacology.org), which provides more detailed views of target and ligand properties.
    [Show full text]
  • Replicated Risk Nicotinic Cholinergic Receptor Genes for Nicotine Dependence
    G C A T T A C G G C A T genes Article Replicated Risk Nicotinic Cholinergic Receptor Genes for Nicotine Dependence Lingjun Zuo 1, Rolando Garcia-Milian 2, Xiaoyun Guo 1,3,4,*, Chunlong Zhong 5,*, Yunlong Tan 6, Zhiren Wang 6, Jijun Wang 3, Xiaoping Wang 7, Longli Kang 8, Lu Lu 9,10, Xiangning Chen 11,12, Chiang-Shan R. Li 1 and Xingguang Luo 1,6,* 1 Department of Psychiatry, Yale University School of Medicine, New Haven, CT 06510, USA; [email protected] (L.Z.); [email protected] (C.-S.R.L.) 2 Curriculum & Research Support Department, Cushing/Whitney Medical Library, Yale University School of Medicine, New Haven, CT 06510, USA; [email protected] 3 Shanghai Mental Health Center, Shanghai 200030, China; [email protected] 4 Department of Cellular and Molecular Physiology, Yale University School of Medicine, New Haven, CT 06510, USA 5 Department of Neurosurgery, Ren Ji Hospital, School of Medicine, Shanghai Jiao Tong University, Shanghai 200127, China 6 Biological Psychiatry Research Center, Beijing Huilongguan Hospital, Beijing 100096, China; [email protected] (Y.T.); [email protected] (Z.W.) 7 Department of Neurology, Shanghai First People’s Hospital, Shanghai Jiao Tong University, Shanghai 200080, China; [email protected] 8 Key Laboratory for Molecular Genetic Mechanisms and Intervention Research on High Altitude Diseases of Tibet Autonomous Region, Xizang Minzu University School of Medicine, Xianyang, Shanxi 712082, China; [email protected] 9 Provincial Key Laboratory for Inflammation and Molecular Drug Target, Medical
    [Show full text]
  • Arthrogryposis and Congenital Myasthenic Syndrome Precision Panel
    Arthrogryposis and Congenital Myasthenic Syndrome Precision Panel Overview Arthrogryposis or arthrogryposis multiplex congenita (AMC) is a group of nonprogressive conditions characterized by multiple joint contractures found throughout the body at birth. It usually appears as a feature of other neuromuscular conditions or part of systemic diseases. Primary cases may present prenatally with decreased fetal movements associated with joint contractures as well as brain abnormalities, decreased muscle bulk and polyhydramnios whereas secondary causes may present with isolated contractures. Congenital Myasthenic Syndromes (CMS) are a clinically and genetically heterogeneous group of disorders characterized by impaired neuromuscular transmission. Clinically they usually present with abnormal fatigability upon exertion, transient weakness of extra-ocular, facial, bulbar, truncal or limb muscles. Severity ranges from mild, phasic weakness, to disabling permanent weakness with respiratory difficulties and ultimately death. The mode of inheritance of these diseases typically follows and autosomal recessive pattern, although dominant forms can be seen. The Igenomix Arthrogryposis and Congenital Myasthenic Syndrome Precision Panel can be as a tool for an accurate diagnosis ultimately leading to a better management and prognosis of the disease. It provides a comprehensive analysis of the genes involved in this disease using next-generation sequencing (NGS) to fully understand the spectrum of relevant genes involved, and their high or intermediate penetrance.
    [Show full text]
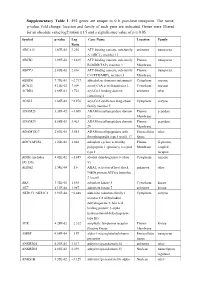
  • Supplementary Table 1
    Supplementary Table 1. 492 genes are unique to 0 h post-heat timepoint. The name, p-value, fold change, location and family of each gene are indicated. Genes were filtered for an absolute value log2 ration 1.5 and a significance value of p ≤ 0.05. Symbol p-value Log Gene Name Location Family Ratio ABCA13 1.87E-02 3.292 ATP-binding cassette, sub-family unknown transporter A (ABC1), member 13 ABCB1 1.93E-02 −1.819 ATP-binding cassette, sub-family Plasma transporter B (MDR/TAP), member 1 Membrane ABCC3 2.83E-02 2.016 ATP-binding cassette, sub-family Plasma transporter C (CFTR/MRP), member 3 Membrane ABHD6 7.79E-03 −2.717 abhydrolase domain containing 6 Cytoplasm enzyme ACAT1 4.10E-02 3.009 acetyl-CoA acetyltransferase 1 Cytoplasm enzyme ACBD4 2.66E-03 1.722 acyl-CoA binding domain unknown other containing 4 ACSL5 1.86E-02 −2.876 acyl-CoA synthetase long-chain Cytoplasm enzyme family member 5 ADAM23 3.33E-02 −3.008 ADAM metallopeptidase domain Plasma peptidase 23 Membrane ADAM29 5.58E-03 3.463 ADAM metallopeptidase domain Plasma peptidase 29 Membrane ADAMTS17 2.67E-04 3.051 ADAM metallopeptidase with Extracellular other thrombospondin type 1 motif, 17 Space ADCYAP1R1 1.20E-02 1.848 adenylate cyclase activating Plasma G-protein polypeptide 1 (pituitary) receptor Membrane coupled type I receptor ADH6 (includes 4.02E-02 −1.845 alcohol dehydrogenase 6 (class Cytoplasm enzyme EG:130) V) AHSA2 1.54E-04 −1.6 AHA1, activator of heat shock unknown other 90kDa protein ATPase homolog 2 (yeast) AK5 3.32E-02 1.658 adenylate kinase 5 Cytoplasm kinase AK7
    [Show full text]
  • Resequencing of Nicotinic Acetylcholine Receptor Genes and Association of Common and Rare Variants with the Fagerstro¨M Test for Nicotine Dependence
    Neuropsychopharmacology (2010) 35, 2392–2402 & 2010 Nature Publishing Group All rights reserved 0893-133X/10 $32.00 www.neuropsychopharmacology.org Resequencing of Nicotinic Acetylcholine Receptor Genes and Association of Common and Rare Variants with the Fagerstro¨m Test for Nicotine Dependence 1,4 1 2 2 1 Jennifer Wessel , Sarah M McDonald , David A Hinds , Renee P Stokowski , Harold S Javitz , 2 1 2 1 2 1 Michael Kennemer , Ruth Krasnow , William Dirks , Jill Hardin , Steven J Pitts , Martha Michel , 1 2 3 1 ,1 Lisa Jack , Dennis G Ballinger , Jennifer B McClure , Gary E Swan and Andrew W Bergen* 1 2 3 Center for Health Sciences, SRI International, Menlo Park, CA, USA; Perlegen Sciences, Mountain View, CA, USA; Group Health Research 4 Institute, Seattle, WA, USA; Department of Public Health, Indiana University School of Medicine, Indianapolis, IN, USA Common single-nucleotide polymorphisms (SNPs) at nicotinic acetylcholine receptor (nAChR) subunit genes have previously been associated with measures of nicotine dependence. We investigated the contribution of common SNPs and rare single-nucleotide variants (SNVs) in nAChR genes to Fagerstro¨m test for nicotine dependence (FTND) scores in treatment-seeking smokers. Exons of 10 genes were resequenced with next-generation sequencing technology in 448 European-American participants of a smoking cessation trial, and CHRNB2 and CHRNA4 were resequenced by Sanger technology to improve sequence coverage. A total of 214 SNP/SNVs were identified, of which 19.2% were excluded from analyses because of reduced completion rate, 73.9% had minor allele frequencies o5%, and 48.1% were novel relative to dbSNP build 129.
    [Show full text]
  • Profile of the Nicotinic Cholinergic Receptor Alpha 7 Subunit Gene Expression Is Associated with Response to Varenicline Treatment
    Profile of the nicotinic cholinergic receptor alpha 7 subunit gene expression is associated with response to varenicline treatment Juliana Rocha Santos1, Paulo Roberto Xavier Tomaz1, Jaqueline Scholz2, Patrícia Viviane Gaya2, Tânia Ogawa Abe2, José Eduardo Krieger1, Alexandre Costa Pereira1, Paulo Caleb Júnior Lima Santos3* 1 Laboratory of Genetics and Molecular Cardiology, Instituto do Coracao (InCor), Hospital das Clinicas HCFMUSP, Faculdade de Medicina, Universidade de Sao Paulo, Sao Paulo, Brazil. 2 Smoking Cessation Program Department, Instituto do Coracao (InCor), Hospital das Clinicas HCFMUSP, Faculdade de Medicina, Universidade de Sao Paulo, Sao Paulo, Brazil. 3 Department of Pharmacology – Escola Paulista de Medicina, Universidade Federal de Sao Paulo, EPM-Unifesp, Sao Paulo, Brazil. Supplementary table 1 - Median values of ∆CT genes according with time periods and outcome groups Resistant T0 Resistant T2 Resistant T4 ∆CT IC 95% ∆CT IC 95% ∆CT IC 95% CHRNA5 8.18 (7.32 – 8.70) 8.45 (7.48 – 8.87) 7.67 (7.27 – 9.05) CHRNA7 6.62 (6.17 – 6.97) 8.02 (7.07 – 8.48) 7.19 (6.96 – 7.86) CHRNG 6.20 (5.79 – 6.95) 6.47 (6.01 – 6.68) 6.63 (6.02 – 7.02) COMT 4.67 (4.40– 5.01) 4.80 (4.43 – 5.03) 4.87 (4.52 – 5.24) Success T0 Success T2 Success T4 ∆CT IC 95% ∆CT IC 95% ∆CT IC 95% CHRNA5 8.32 (7.38 – 9.17) 7.07 (6.53 – 8.96) 8.37 (7.54 – 8.82) CHRNA7 7.26 (6.11 – 8.42) 7.04 (6.40 – 7.79) 7.38 (6.76 – 8.20) CHRNG 6.82 (6.19 – 7.74) 6.83 (6.56 – 7.33) 6.59 (6.25 – 7.03) COMT 4.88 (4.30 – 5.11) 4.58 (4.33 -5.15) 4.81 (4.48 – 5.16) ∆CT = (CT target gene – CThousekeepings genes mean).
    [Show full text]
  • The Neuromuscular Junction Is a Focal Point of Mtorc1 Signaling in Sarcopenia
    ARTICLE https://doi.org/10.1038/s41467-020-18140-1 OPEN The neuromuscular junction is a focal point of mTORC1 signaling in sarcopenia Daniel J. Ham 1,4, Anastasiya Börsch1,4, Shuo Lin1, Marco Thürkauf1, Martin Weihrauch1, Judith R. Reinhard1, Julien Delezie1, Fabienne Battilana1, Xueyong Wang2, Marco S. Kaiser 1, Maitea Guridi1, Michael Sinnreich3, Mark M. Rich 2, Nitish Mittal1, Lionel A. Tintignac3, Christoph Handschin 1, Mihaela Zavolan 1,4 & ✉ Markus A. Rüegg 1,4 1234567890():,; With human median lifespan extending into the 80s in many developed countries, the societal burden of age-related muscle loss (sarcopenia) is increasing. mTORC1 promotes skeletal muscle hypertrophy, but also drives organismal aging. Here, we address the question of whether mTORC1 activation or suppression is beneficial for skeletal muscle aging. We demonstrate that chronic mTORC1 inhibition with rapamycin is overwhelmingly, but not entirely, positive for aging mouse skeletal muscle, while genetic, muscle fiber-specific acti- vation of mTORC1 is sufficient to induce molecular signatures of sarcopenia. Through inte- gration of comprehensive physiological and extensive gene expression profiling in young and old mice, and following genetic activation or pharmacological inhibition of mTORC1, we establish the phenotypically-backed, mTORC1-focused, multi-muscle gene expression atlas, SarcoAtlas (https://sarcoatlas.scicore.unibas.ch/), as a user-friendly gene discovery tool. We uncover inter-muscle divergence in the primary drivers of sarcopenia and identify the neuromuscular junction as a focal point of mTORC1-driven muscle aging. 1 Biozentrum, University of Basel, Basel, Switzerland. 2 Department of Neurology, Neuroscience, Cell Biology, and Physiology, Wright State University, Dayton, OH, USA. 3 Department of Biomedicine, Pharmazentrum, University of Basel, Basel, Switzerland.
    [Show full text]
  • GENETIC of ADDICTION: COMMON and UNCOMMON FACTORS Giada Juli1 & Luigi Juli2 1Catanzaro, Italy 2Mental Health Department, Catanzaro, Italy
    Psychiatria Danubina, 2015; Vol. 27, Suppl. 1, pp 383–390 Conference paper © Medicinska naklada - Zagreb, Croatia GENETIC OF ADDICTION: COMMON AND UNCOMMON FACTORS Giada Juli1 & Luigi Juli2 1Catanzaro, Italy 2Mental Health Department, Catanzaro, Italy SUMMARY Epidemiological studies strongly suggest that genetic factors operate at all steps of addictions, including vulnerability to initiation, continued use, and propensity to become dependent. Several studies have been popular to investigate the relative contributions of genetic and environmental factors, including the availability of and exposure to a substance, and shared and unique environments. The genetic influence on addiction has proved to be substantial, and heritabilities for most addictive disorders are moderate to high. In this work we evaluate the current status of data that analyzed genetic contribution in addictions. Key words: addictions- genetic factors-dependence * * * * * INTRODUCTION have analyzed alcohol addiction (or alcohol depen- dence) but the genetic influence have been evaluated Addiction is characterized by a compulsion to take a also for the susceptibility of tobacco addiction (or substance, with goal-directed behavior toward excessive dependence), cannabis, opioids and other psychoactive substance intake and a loss of control in limiting intake. substances. The aim of this review is to summarize the Recently, the Addictive Disorders have been enri- available literature that underly common and un- ched not only by synthetic substances of use/abuse, but common factors in genetic of addictions. also by behaviors capable to promote psychopatho- logical states which are disabling and serious. In fact, ALCOHOL DEPENDENCE (AD) apart from alcohol, tobacco, cocaine, cannabis, heroin and other substances, science has identified new addic- It is known that alcohol dependence (AD) can be tions such as Eating Disorders (Juli 2014), Gambling considered as a familiar trait with well characterized Addiction, Internet and Sex Addiction.
    [Show full text]
  • Pharmacogenomics of Drug Addiction
    FACULDADE DE FARMÁCIA UNIVERSIDADE DE COIMBRA Mestrado em Biotecnologia Farmacêutica Dissertação Pharmacogenomics of Drug Addiction Dissertação apresentada à Faculdade de Farmácia da Universidade de Coimbra, para cumprimento dos requisitos necessários à obtenção do grau de Mestre em Biotecnologia Farmacêutica, realizada sob a orientação científica da Professora Doutora Maria Manuela Monteiro Grazina (Faculdade de Medicina da Universidade de Coimbra) e orientação interna do Professor Doutor Sérgio Simões (Faculdade de Farmácia da Universidade de Coimbra). Carolina Macedo, 2014 Copyright © Carolina Macedo & Manuela Grazina, 2014 Esta cópia da tese é fornecida na condição de que quem a consulta reconhece que os direitos de autor são pertença do autor da tese e do orientador científico e que nenhuma citação ou informação obtida a partir dela pode ser usada ou publicada sem a referência apropriada após autorização pela responsável do estudo, a Professora Doutora Manuela Grazina. This copy of the thesis has been supplied on condition that anyone who consults it is understood to recognize that its copyright belongs to its author and scientific supervisor and that no quotation from the thesis and no information derived from it can be used or published without the appropriate reference upon authorization by the coordinator of the study, Professor Manuela Grazina. Epigraph For every complex problem there is an answer that is clear, simple, and wrong. H. L. Mecken Agradecimentos À Professora Doutora Manuela Grazina por ter aceite orientar a minha dissertação e por me ter proposto este tema tão desafiante e complexo. Ao Professor Doutor Sérgio Simões por ter sido meu co-orientador, pela Faculdade de Farmácia da Universidade de Coimbra.
    [Show full text]
  • Research Article Complex and Multidimensional Lipid Raft Alterations in a Murine Model of Alzheimer’S Disease
    SAGE-Hindawi Access to Research International Journal of Alzheimer’s Disease Volume 2010, Article ID 604792, 56 pages doi:10.4061/2010/604792 Research Article Complex and Multidimensional Lipid Raft Alterations in a Murine Model of Alzheimer’s Disease Wayne Chadwick, 1 Randall Brenneman,1, 2 Bronwen Martin,3 and Stuart Maudsley1 1 Receptor Pharmacology Unit, National Institute on Aging, National Institutes of Health, 251 Bayview Boulevard, Suite 100, Baltimore, MD 21224, USA 2 Miller School of Medicine, University of Miami, Miami, FL 33124, USA 3 Metabolism Unit, National Institute on Aging, National Institutes of Health, 251 Bayview Boulevard, Suite 100, Baltimore, MD 21224, USA Correspondence should be addressed to Stuart Maudsley, [email protected] Received 17 May 2010; Accepted 27 July 2010 Academic Editor: Gemma Casadesus Copyright © 2010 Wayne Chadwick et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Various animal models of Alzheimer’s disease (AD) have been created to assist our appreciation of AD pathophysiology, as well as aid development of novel therapeutic strategies. Despite the discovery of mutated proteins that predict the development of AD, there are likely to be many other proteins also involved in this disorder. Complex physiological processes are mediated by coherent interactions of clusters of functionally related proteins. Synaptic dysfunction is one of the hallmarks of AD. Synaptic proteins are organized into multiprotein complexes in high-density membrane structures, known as lipid rafts. These microdomains enable coherent clustering of synergistic signaling proteins.
    [Show full text]
  • Carrier Screen Genes List
    Gene Disease ABCB11 Cholestasis, progressive familial intrahepatic 2 ABCB11 Cholestasis, benign recurrent intrahepatic, 2 ABCC2 Dubin-Johnson syndrome ABCC8 Diabetes, noninsulin dependent ABCC8 Diabetes, permanent neonatal ABCC8 Hyperinsulinemic hypoglycemia, familial, 1 ABCC8 Hypoglycemia, infantile ABCD1 Adrenoleukodystrophy ACADM Acyl-CoA dehydrogenase, medium chain, deficiency of ACADS Acyl-CoA dehydrogenase, short-chain, deficiency of ACADVL Acyl-CoA dehydrogenase, very long-chain, deficiency of ACAT1 Alpha-methylacetoacetic aciduria ACOX1 Peroxisomal acyl-CoA oxidase deficiency ACTA1 Myopathy congenital, with fiber-type disproportion ACTA1 Nemaline myopathy 3, AD or recessive ADA Severe combined immunodeficiency due to ADA deficiency ADAMTS2 Ehlers-Danlos syndrome AGA Aspartylglucosaminuria AGL Glycogen storage disease IIIa, IIb AGXT Hyperoxaluria, primary, type 1 AHCY Hypermethioninemia with deficiency of S-adenosylhomocysteine hydrolase Autoimmune polyendocrinopathy syndrome , type I, with or without reversible metaphyseal AIRE dysplasia ALDH3A2 Sjogren-Larsson syndrome ALDH4A1 Hyperprolinemia type II ALDOB Fructose intolerance, hereditary ALG6 Congenital disorder of glycosylation, type Ic ALPL Hypophosphatasia AMH Persistent Mullerian duct syndrome, type I AMHR2 Persistent Mullerian duct syndrome, type II AMPD1 Myopathy due to myoadenylate deaminase deficiency AMT Glycine encephalopathy AR Androgen insensitivity AR Androgen insensitivity AR Hypospadias AR Spinal and bulbar muscular atrophy of Kennedy ARG1 Argininemia ARL13B Joubert
    [Show full text]