Scour Prediction at Srisailam Dam (India)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dam Inflow Prediction by Using Artificial Neural Network Reservoir Computing
International Journal of Engineering and Advanced Technology (IJEAT) ISSN: 2249 – 8958, Volume-9 Issue-2, December, 2019 Dam Inflow Prediction by using Artificial Neural Network Reservoir Computing B. Pradeepakumari, Kota Srinivasu Abstract; A multipurpose dam serves multiple modalities like A practical approach for water management is agriculture, hydropower, industry, daily usage. Generally dam presented with case study in work [2]. On the other hand water level and inflow are changing throughout the year. So, [3,4] has highlighted importance of inflow predictions for multipurpose dams require effective water management strategies water management. Classical rainfall and runoff models in place for efficient utilization of water. Discrepancy in water exist, such as empirical, conceptual, physically, and data- management may lead to significant socio-economic losses and may have effect on agriculture patterns in surrounding areas. driven [5,6]. Data-driven models in different fields of water Inflow is one of the dynamic driving factors in water resources with [7,8,9] can be modeled effectively for water management. So accurate inflow forecasting is necessary for management. At the same time, researchers have realized effective water management. complex nature of relationship between rainfall and runoff For inflow forecasting various methods are used by researchers. so various complex models are introduced like fuzzy logic Among them Auto Regressive Integrated Moving Average [10], support vector regression [11], and Artificial Neural (ARIMA) and Artificial Neural Network (ANN) techniques are Networks (ANN) [6,12]. Neural networks have been widely most popular. Both of these techniques have shown significant applied as an effective method for modeling highly contribution in various domains in regards to forecasting. -

6. Water Quality ------61 6.1 Surface Water Quality Observations ------61 6.2 Ground Water Quality Observations ------62 7
Version 2.0 Krishna Basin Preface Optimal management of water resources is the necessity of time in the wake of development and growing need of population of India. The National Water Policy of India (2002) recognizes that development and management of water resources need to be governed by national perspectives in order to develop and conserve the scarce water resources in an integrated and environmentally sound basis. The policy emphasizes the need for effective management of water resources by intensifying research efforts in use of remote sensing technology and developing an information system. In this reference a Memorandum of Understanding (MoU) was signed on December 3, 2008 between the Central Water Commission (CWC) and National Remote Sensing Centre (NRSC), Indian Space Research Organisation (ISRO) to execute the project “Generation of Database and Implementation of Web enabled Water resources Information System in the Country” short named as India-WRIS WebGIS. India-WRIS WebGIS has been developed and is in public domain since December 2010 (www.india- wris.nrsc.gov.in). It provides a ‘Single Window solution’ for all water resources data and information in a standardized national GIS framework and allow users to search, access, visualize, understand and analyze comprehensive and contextual water resources data and information for planning, development and Integrated Water Resources Management (IWRM). Basin is recognized as the ideal and practical unit of water resources management because it allows the holistic understanding of upstream-downstream hydrological interactions and solutions for management for all competing sectors of water demand. The practice of basin planning has developed due to the changing demands on river systems and the changing conditions of rivers by human interventions. -

Chapter 5 Water Resources and Hydrology
Chapter 5 Water Resources and Hydrology 5.1 General Planning for water resources development in a basin requires careful assessment of the available water resources and reasonable needs of the basin in foreseeable future for various purposes such as drinking, irrigation, hydro-power, industries, navigation etc. Hydrological studies are carried out to assess the available quantity of water in a given basin. This chapter deals with the assessment of water balance in the Krishna basin upto the Nagarjunasagar dam site, in the basins lying enroute the link alignment, in the Pennar basin upto the Somasila dam site and simulation study of Nagarjunasagar reservoir. 5.2 Hydrological analysis NWDA has prepared water balance study reports at Nagarjunasagar dam site on river Krishna, Somasila dam site on river Pennar and of the basins lying enroute the link alignment. The methodology adopted by NWDA for computing the water balance of a sub-basin is discussed in the following paragraphs: 5.2.1 Surface water availability Observed flow data at the terminal G&D site and the rainfall observed at various raingauge stations in and around the catchment of a sub-basin are collected. To the observed flows, year-wise upstream utilisations are added to get virgin yields. Weighted rainfall for the catchment upto the G&D site and for the whole sub-basin is worked out. Using these virgin flows and weighted rainfall upto the G&D site, a rainfall - runoff relationship (linear/non-linear) is developed by statistical methods. Using the best fit equation and weighted rainfall for the entire sub-basin, monsoon yields are computed. -

List of Dams in India: State Wise
ambitiousbaba.com Online Test Series List of Dams in India: State Wise State DAM and Location Rajasthan • RanapratapSagar Dam(Chambal River), at Rawatbhata • Mahi Bajaj Sagar Dam (Mahi River) at Banswara district • Bisalpur Dam (Banas River), At Tonk district • Srisailam Dam(Krishna River), at Kurnool Andhra Pradesh district • Somasila Dam (Penna River), at Nellore district • Prakasam Barrage (Krishna River), at Krishna and Guntur • Tatipudi Reservoir(River Gosthani ), at Tatipudi, Vizianagaram • Gandipalem Reservoir (River Penner) • Ramagundam dam (Godavari), in Karimnagar • Dummaguden Dam (river Godavari) Telangana • Nagarjuna Sagar Dam (Krishna river), at Nagarjuna Sagar Nalgonda • Sri Ram Sagar (River Godavari) • Nizam Sagar Dam (Manjira River) • Dindi Reservoir (River Krishna), at Dindi, Mahabubnagar town • Lower Manair Dam (Manair River) • Singur Dam (river Manjira) Bihar • Kohira Dam (Kohira River), at Kaimur district • Nagi Dam (Nagi River), in Jamui District Chhattisgarh • HasdeoBango Dam (Hasdeo River), at Korba district Gujarat • SardarSarovar Dam(Narmada river), at Navagam • Ukai Dam(Tapti River), at Ukai in Tapi district IBPS | SBI | RBI | SEBI | SIDBI | NABARD | SSC CGL | SSC CHSL | AND OTHER GOVERNMENT EXAMS 1 ambitiousbaba.com Online Test Series • Kadana Dam( Mahi River), at Panchmahal district • Karjan Reservoir (Karjan river), at Jitgadh village of Nanded Taluka, Dist. Narmada Himachal Pradesh • Bhakra Dam (Sutlej River) in Bilaspur • The Pong Dam (Beas River ) • The Chamera Dam (River Ravi) at Chamba district J & K -

Dams in Telangana State an Incredible Challenge Confronted In
Dams in Telangana State An Incredible Challenge Confronted in effectively managing the Probable Maximum flood Neelam Sanjeev Reddy Sagar Dam (NSRSP) Location - A Case Study. Presented By: P.Shalini, Assistant Executive Engineer, O/o The Chief Engineer, I&CAD Dept, Govt of Telangana. 1 CONTENTS Page No 1. Introduction 4 1.1 Dams In Telangana State 4 1.2 Projects under Godavari Basin 4 1.3 Projects under Krishna Basin 5 2. Neelam Sanjeev Reddy Sagar Dam 6 2.1 Challenge 6 2.2 The October 2009 Floods 7 3. Rainfall and Water Allocation 7 3.1 Projects on Krishna River 7 3.2 Drought Situation 7 3.3 Flood Situation 8 3.4 Probable Maximum Flood 8 3.5 The Nagarjunsagar Dam 8 3.6 The Prakasam Barrage 8 4. Rainfall Forecast 9 4.1 IMD forecast 9 4.2 CWC forecast 9 4.3 Real Time Monitoring of Flood and 9 Modelling 5. Reference to Course Material 14 6. Summary 15 7. Conclusion 15 2 List of Figures and Maps Page No Fig.1: Main Reservoirs on River Krishna 7 Fig.2: Nagarjun Sagar Dam 8 Fig.3: Prakasam Barrage 8 Fig.4: Max Water level at Srisailam 10 Fig.5: Innundated Power house at Srisailam dam 10 Fig.6: Srisailam dam and reservoir 11 Fig.7: Downstream view of Srisailam dam 11 Fig.8: An ariel view of the Srisailam dam with +896.50 feet at water level 11 Fig.9: Upstream side of Srisailam dam heavy inflows 11 Fig.10: Maximum outflow through spillway at Srisailam dam 11 Fig.11: A view of downstream of Srisailam dam during opening of all 12 gates 11 Fig.12: Map showing Inflows at Srisailam dam between September 30 13 to October 12,2009 Fig.13: Map showing Outflows at Srisailam dam between September 30 13 to October 12, 2009 Fig.14: Map showing gross capacity at Srisailam dam between September 30 13 to October 12, 2009 Fig.15: Possible Inundation Map of Srisailam Dam break 17 3 1. -

Summary Report on Water Use Efficiency Studies for 35 Irrigation Projects
Summary Report On Water Use Efficiency Studies For 35 Irrigation Projects Organized by Performance Overview & Management Improvement Organization Central Water Commission Government of India February, 2016 1 Contents S.No TITLE Page No Prologue 3 I Abbreviations 4 II SUMMARY OF WUE STUDIES 5 ANDHRA PRADESH 1 Bhairavanthippa Project 6-7 2 Gajuladinne (Sanjeevaiah Sagar Project) 8-11 3 Gandipalem project 12-14 4 Godavari Delta System (Sir Arthur Cotton Barrage) 15-19 5 Kurnool-Cuddapah Canal System 20-22 6 Krishna Delta System(Prakasam Barrage) 23-26 7 Narayanapuram Project 27-28 8 Srisailam (Neelam Sanjeeva Reddy Sagar Project)/SRBC 29-31 9 Somsila Project 32-33 10 Tungabadhra High level Canal 34-36 11 Tungabadhra Project Low level Canal(TBP-LLC) 37-39 12 Vansadhara Project 40-41 13 Yeluru Project 42-44 ANDHRA PRADESH AND TELANGANA 14 Nagarjuna Sagar project 45-48 TELANGANA 15 Kaddam Project 49-51 16 Koli Sagar Project 52-54 17 NizamSagar Project 55-57 18 Rajolibanda Diversion Scheme 58-61 19 Sri Ram Sagar Project 62-65 20 Upper Manair Project 66-67 HARYANA 21 Augmentation Canal Project 68-71 22 Naggal Lift Irrigation Project 72-75 PUNJAB 23 Dholabaha Dam 76-78 24 Ranjit Sagar Dam 79-82 UTTAR PRADESH 25 Ahraura Dam Irrigation Project 83-84 26 Walmiki Sarovar Project 85-87 27 Matatila Dam Project 88-91 28 Naugarh Dam Irrigation Project 92-93 UTTAR PRADESH & UTTRAKHAND 29 Pilli Dam Project 94-97 UTTRAKHAND 30 East Baigul Project 98-101 BIHAR 31 Kamla Irrigation project 102-104 32 Upper Morhar Irrigation Project 105-107 33 Durgawati Irrigation -

Blueprint for Godavari River Water Utilisation In
BLUE PRINT FOR GODAVARI RIVER WATER UTILIZATION IN ANDHRA PRADESH N. Sasidhar. Abstract: This paper explains how the unutilized Godavari river water could be put to use fully for irrigation with the help of water powered pump units and pumped storage schemes without proposing inter state dam projects. This paper also proposes how the available water in Godavari and Krishna rivers could be used for irrigating most of upland areas in Telangana and Rayalaseema regions with optimum pumping power. Godavari is the largest river of all peninsular rivers in India. It has a total drainage area of 312,812 square km of which 48.6% lies in Maharashtra, 23.8% in Andhra Pradesh (AP), 18.7% in Chattisgarh, 5.5% in Orissa, 2% in Madhya Pradesh (MP) and 1.4 % in Karnataka. Principal tributaries of Godavari are Pranhita, Indravati and Sabari. All these tributaries drain water from high rainfall areas (i.e. more than 100 cm annual rain fall) except the main river Godavari. These tributaries contribute 80% flow of the total river. The average yearly water flow in Godavari is nearly 110 billion cubic meters. Pranhita drains Vidarbha region and joins the main river near Kaleswaram temple town in AP at 95 meters Mean Sea Level (m MSL). Indravati traverses through parts of Orissa and southern part of Chattisgarh and joins main river upstream of proposed inter state dam project at Inchampalli in AP. Sabari drains from parts of Orissa and Chattisgarh and joins the main river upstream of proposed Polavaram dam in AP. WATER AVAILABILITY: The water available in the upper reaches of Godavari up to Pranhita tributary confluence are fully utilized by Maharashtra, Karnataka and AP by developing various irrigation projects. -

Central Water Commission Special Advisories in Association with Deep Depression 13-10-2020 at 1700 Hrs 1. Meteorological Situation
Central Water Commission Special Advisories in association with Deep Depression 13-10-2020 at 1700 hrs 1. Meteorological Situation Deep Depression crossed north Andhra Pradesh coast close to Kakinada during the early morning of 13th October 2020 and is now seen as a Depression about 95 km west northwest of Kakinada. Due to this extremely heavy to very heavy rainfall (in cm) occurred at the following places: Andhra Pradesh & Yanam - Yanam-25; Amalapuram, Tanuku & Nuzbid-19 each; Tadepalligudem-18; Vijaywada & Bheemunipatnam-16 each; Kaikalur, Palasa, Ichchapuram & Tiruvuru-15 each; Velamanchili-14; Chintalapudi, Sompeta, Gudibada & Mandasa-13 each; Telangana - Sathupalle- 19, Mahabubabad-13 and Odisha - Mohana-14. Basinwise rainfall distribution indicates that Krishna and Godavari Basin have received Excess Rainfall for the second consecutive Day as indicated in the Map below: 1.2 Rainfall forecast for next 5 days issued on 13th October, 2020 (Midday) by IMD Rainfall Forecast Date Extremely heavy Very heavy 13/10/2020 Telangana and adjoining Districts of North Interior Coastal Karnataka and remaining Districts of North Interior Karnataka, South Karnataka Konkan & Goa, Madhya Maharashtra and Marathwada 14/10/2020 Madhya Maharashtra, South Konkan & Goa North Konkan, North Interior Karnataka and Marathwada 2 CWC Advisories Krishna Basin Due to forecasted rainfall, inflows into all dams in Krishna Basin are likely to increase rapidly. Increased Inflows into Narayanpur Dam, Tungabhadra Dam have been witnessed. Due to very heavy rainfall in its catchments, rivers Paleru, Munneru and its tributary Wyra are rising rapidly in Khammam District in Telangana and Krishna District in Andhra Pradesh. Hydrograph of river Wyra at Madhira in Khammam District and river Munneru at Keesara in Krishna District are appended. -

Explaining Basin Closure in the Lower Krishna Basin, South India
RESEARCH REPORT Shifting Waterscapes: 121 Explaining Basin Closure in the Lower Krishna Basin, South India Jean-Philippe Venot, Hugh Turral, Madar Samad and François Molle International Water Management IWMI is a Future Harvest Center Institute supported by the CGIAR Research Reports IWMI’s mission is to improve water and land resources management for food, livelihoods and nature. In serving this mission, IWMI concentrates on the integration of policies, technologies and management systems to achieve workable solutions to real problems—practical, relevant results in the field of irrigation and water and land resources. The publications in this series cover a wide range of subjects—from computer modeling to experience with water user associations—and vary in content from directly applicable research to more basic studies, on which applied work ultimately depends. Some research reports are narrowly focused, analytical and detailed empirical studies; others are wide-ranging and synthetic overviews of generic problems. Although most of the reports are published by IWMI staff and their collaborators, we welcome contributions from others. Each report is reviewed internally by IWMI’s own staff and Fellows, and by external reviewers. The reports are published and distributed both in hard copy and electronically (www.iwmi.org) and where possible all data and analyses will be available as separate downloadable files. Reports may be copied freely and cited with due acknowledgment. Research Report 121 Shifting Waterscapes: Explaining Basin Closure in the Lower Krishna Basin, South India Jean-Philippe Venot, Hugh Turral, Madar Samad and François Molle International Water Management Institute P O Box 2075, Colombo, Sri Lanka i i IWMI receives its principal funding from 58 governments, private foundations, and international and regional organizations known as the Consultative Group on International Agricultural Research (CGIAR). -

Introduction of WRD in AP & Its Development in India
1 Introduction of WRD in AP & its Development in India &AP set up, mandate and functions of various wings of WRD & Organ gram (Dr I Satyanarayana Raju, Former Chief Engineer, CDO, Hyderabad, &Member, TAC-WRD, AP) A. Introduction: The erstwhile Andhra Pradesh is geographically spread in 2.75 lakh Sq Km and accounts for 8.4% of the total geographical area with a population over 80 million.A.P is basically agricultural predominant state and 75% of population depends on agriculture as their livelihood. So also the state is blessed with major rivers viz., Godavari, Krishna, Penna and Vamsadhara and other 36 medium and minor rivers flowing in the state. On 2nd June 2014, the new Telangana state is formed as 29th state of India with the 10 districts of Telangana region and now the rest 13 districts of Coastal Andhra and Rayalaseema remained with residual AP. The Geographical area of this AP is 1, 60,205 Sq.km and population is 4.94 million. It got long coastline of 972 km and annual rainfall ranges 1300-600mm. B. Main Functions of Water Resources Department: The main functions of the Department are: 1) Preparation and implementation of operation and maintenance plans for existing irrigation projects. 2) Improve water management and efficiency by the integrated and coordinated efforts by all line departments. 3) Stabilization of existing ayacut by rehabilitation of the age old projects. 4) Modernization of age old major and medium irrigation projects. 5) Flood management. 6) Restoration and maintenance of river flood banks. 7) Irrigation assessment and assessment of water royalty charges for industrial and other utilization. -
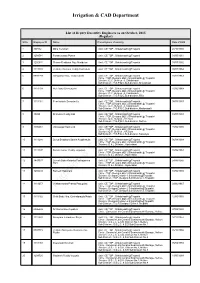
Deputy Executive Engineers As on October, 2015 (Regular)
Irrigation & CAD Department List of Deputy Executive Engineers as on October, 2015 (Regular) S.No. Employee ID Name Present place of working Date of Birth 1 807932 Mitra Yenubari Unit : CE TGP , Srikalahasthi@Tirupathi 20/10/1960 2 1209581 Parameswara Ponna Unit : CE TGP , Srikalahasthi@Tirupathi 01/05/1961 3 1202931 Chinna Reddaiah Raju Mudduluri Unit : CE TGP , Srikalahasthi@Tirupathi 01/07/1962 4 1113203 Venkata Ramana Reddy Kushakula Unit : CE TGP , Srikalahasthi@Tirupathi 08/07/1964 5 0808189 Gangadhar Rao Thalamanchi Unit : CE TGP , Srikalahasthi@Tirupathi 01/07/1963 Circle : TGP,(Designs &QC) Srikalahasthi @ Tirupathi Division : Q.C. Division -3, Srikalahasti Sub Division : T.G.P.Q.C.Sub-division, Srikalahasti 6 1113154 Hari Babu Chimakurthi Unit : CE TGP , Srikalahasthi@Tirupathi 10/06/1964 Circle : TGP,(Designs &QC) Srikalahasthi @ Tirupathi Division : Q.C. Division -3, Srikalahasti Sub Division : T.G.P.Q.C.Sub-division, Piler 7 1113161 Penchalaiah Bommisetty Unit : CE TGP , Srikalahasthi@Tirupathi 08/05/1967 Circle : TGP,(Designs &QC) Srikalahasthi @ Tirupathi Division : Q.C. Division -3, Srikalahasti Sub Division : T.G.P.Q.C.Sub-division, Madanapalli 8 10890 Srinivasa Reddy Kolli Unit : CE TGP , Srikalahasthi@Tirupathi 01/07/1963 Circle : TGP,(Designs &QC) Srikalahasthi @ Tirupathi Division : Q.C. Division , KR Dam Sub Division : T.G.P.Q.C.Sub-division, Nellore 9 1105461 Vidyasagar Kamisetti Unit : CE TGP , Srikalahasthi@Tirupathi 15/06/1965 Circle : TGP,(Designs &QC) Srikalahasthi @ Tirupathi Division : Q.C. Division , KR -

Monthly Current Affairs GK Digest: January 2021
Monthly Current Affairs GK Digest: January 2021 CONTENTS BSSUKM signed MoU with NKJ Biofuel Ltd ................................................................................................................................ 5 DRDO & Indian Navy conducted Trial of SAHAYAK-NG ........................................................................................................ 5 Pimpri Chinchwad Municipal Corporation signed MoU with UNDP India .................................................................... 6 Quantum Random Number Generator (QRNG) ....................................................................................................................... 6 Global Pravasi Rishta Portal and Mobile App .......................................................................................................................... 7 6th Digital India Awards 2020 ...................................................................................................................................................... 7 Appointments and Extension on 2nd January 2021 ............................................................................................................. 8 UN’s FAO Named 4 Asian Tea Cultivation Sites as GIAHS .................................................................................................... 8 Defence Ministry signed Agreement with BEL ........................................................................................................................ 9 PM Modi laid Foundation Stone for Light House