FIRST WORKSHEET (1) Samurai Jack Is My Favorite Cartoon Character
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

PREVIEWS Plus!
READ ABOUT THESE ITEMS AND MORE AT PREVIEWSworld.com When a new item’s so hot it can’t wait to be solicited in the next issue of PREVIEWS, you’ll find it here in PREVIEWS Plus! Here’s your last chance to order some of the hottest comics, toys and merchandise before they come to your comic shop! Order these items from your retailer by MONDAY, OCTOBER 24 PREMIER PUBLISHERS MARVEL COMICS .com world DEADPOOL: BACK IN BLACK #1 DEATH OF X #1 SECOND PRINTING SECOND PRINTING AARON KUDER VARIANT SALVA ESPIN VARIANT (W) Jeff Lemire, Charles Soule (W) Cullen Bunn (A/CA) Salva Espin (A/CA) Aaron Kuder AMAZING SPIDER-MAN #19 CAGE #1 SECOND PRINTING During 1984’s Secret Wars, Deadpool What happened eight months ago that SECOND PRINTING GENNDY TARTAKOVSKY VARIANT was introduced to an alien symbiote who set the Inhumans and X-Men on a collision ALEX ROSS VARIANT (W) Genndy Tartakovsky PREVIEWS went on to become Spider-Man’s black course? Find out here! The Inhumans (W) Dan Slott, Christos Gage (A) Genndy Tartakovsky, Stephen DeStefano costume and, eventually, Venom. Okay, travel to Japan where one of the Terrigen (A) Giuseppe Camuncoli & Various (CA) Genndy Tartakovsky okay, maybe that really happened in Clouds creates a shocking new Inhuman. (CA) Alex Ross From the award-winning creator of Deadpool’s Secret Secret Wars. Point The X-Men travel to Muir Island where the Before “Dead No More”... Someone Dexter’s Laboratory, Samurai Jack, and is, did you know that after Spider-Man second Terrigen Cloud causes something in the Amazing Spider-Man’s orbit dies. -

Please Continue on Back If Needed!
DARK HORSE DC: VERTIGO MARVEL CONT. ANGEL AMERICAN VAMPIRE DEADPOOL BPRD ASTRO CITY FANTASTIC FOUR BUFFY FABLES GHOST RIDER CONAN THE BARBARIAN FAIREST GUARDIANS OF THE GALAXY HELLBOY FBP HAWKEYE MASSIVE SANDMAN INDESTRUCTIBLE HULK "THE" STAR WARS TRILLIUM IRON MAN STAR WARS - Brian Wood Classic UNWRITTEN IRON PATRIOT STAR WARS LEGACY WAKE LOKI STAR WARS DARK TIMES IDW MAGNETO DC COMICS BLACK DYNAMITE MIGHTY AVENGERS ACTION COMICS DOCTOR WHO MIRACLEMAN ADVENTURES OF SUPERMAN G.I. JOE MOON KNIGHT ALL-STAR WESTERN G.I. JOE REAL AMERICAN HERO MS MARVEL ANIMAL MAN G.I. JOE SPECIAL MISSIONS NEW AVENGERS AQUAMAN GHOSTBUSTERS NEW WARRIORS BATGIRL GODZILLA NOVA BATMAN JUDGE DREDD ORIGIN II BATMAN / SUPERMAN MY LITTLE PONY PUNISHER BATMAN / SUPERMAN POWERPUFF GIRLS SAVAGE WOLVERINE BATMAN & ---- SAMURAI JACK SECRET AVENGERS BATMAN 66 STAR TREK SHE HULK BATMAN BEYOND UNIVERSE TEENAGE MNT CLASSICS SILVER SURFER BATMAN LIL GOTHAM TEENAGE MUTANT NINJA TURTLES SUPERIOR FOES OF SPIDERMAN BATMAN: THE DARK KNIGHT TRANSFORMERS More Than Meets Eye SUPERIOR SPIDERMAN BATWING TRANSFORMERS Regeneration One SUPERIOR SPIDERMAN TEAM-UP BATWOMAN TRANSFORMERS Robots in Disguise THOR GOD OF THUNDER BIRDS OF PREY IMAGE THUNDERBOLTS CATWOMAN ALEX & ADA UNCANNY AVENGERS CONSTANTINE BEDLAM UNCANNY X-MEN DETECTIVE COMICS BLACK SCIENCE WOLVERINE EARTH 2 BOUNCE WOLVERINE & THE X-MEN FLASH CHEW X-FORCE GREEN ARROW EAST OF WEST X-MEN GREEN LANTERN ELEPHANTMENT X-MEN LEGACY -

Aug CUSTOMER ORDER FORM
OrdErS PREVIEWS world.com duE th 18 aug 2013 aug COMIC THE SHOP’S PREVIEWSPREVIEWS CATALOG CUSTOMER ORDER FORM CUSTOMER 601 7 Aug13 Cover ROF and COF.indd 1 7/3/2013 3:05:51 PM Available only DEADPOOL: “TACO ENTHUSIAST” from your local BLUE T-SHIRT comic shop! Preorder now! THE WALKING DEAD: STREET FIGHTER: DOCTOR WHO: “THE DIXON BROS.” “THE STREETS” “DON’T BLINK” GLOW ZIP HOODIE RED T-SHIRT IN THE DARK T-SHIRT Preorder now! Preorder now! Preorder now 8 Aug 13 COF Apparel Shirt Ad.indd 1 7/3/2013 10:34:19 AM PrETTY DEADLY #1 ImAgE COmICS THE SHAOLIN COWBOY #1 DArk HOrSE COmICS THE SANDmAN: OVErTUrE #1 DC COmICS / VErTIgO VELVET #1 ELFQUEST SPECIAL: ImAgE COmICS THE FINAL QUEST DArk HOrSE COmICS SAmUrAI JACk #1 IDW PUBLISHINg SUPErmAN/WONDEr mArVEL kNIgHTS: WOmAN #1 SPIDEr-mAN #1 DC COmICS mArVEL COmICS Aug13 Gem Page ROF COF.indd 1 7/3/2013 9:04:01 AM Featured Items COMIC BOOKS & GRAPHIC NOVELS The Fox #1 l ARCHIE COMICS Uber Volume 1 Enhanced HC l AVATAR PRESS Imagine Agents #1 l BOOM! STUDIOS The Shadow Now #1 l D. E./DYNAMITE ENTERTAINMENT Cryptozoic Man #1 l D. E./DYNAMITE ENTERTAINMENT Peanuts Every Sunday 1952-1955 HC l FANTAGRAPHICS BOOKS Battling Boy GN/HC l :01 FIRST SECOND Letter 44 #1 l ONI PRESS 1 1 Ben 10 Omniverse Volume 1: Ghost Ship GN l PERFECT SQUARE X-O Manowar Deluxe HC l VALIANT ENTERTAINMENT Miss Peregrine’s Home For Peculiar Children HC l YEN PRESS BOOKS The Superman Files HC l COMICS Doctor Who 50th Anniversary Anthology l DOCTOR WHO Doctor Who: The Vault: Treasures from the First 50 Years HC l DOCTOR WHO Dc Comics Guide To Creating Comics Sc l HOW-TO Star Trek: Mr. -
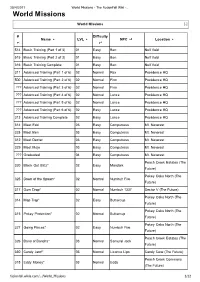
World Missions - the Fusionfall Wiki -… World Missions
20/4/2011 World Missions - The FusionFall Wiki -… World Missions World Missions [-] # Difficulty Name LVL NPC Location 514 Basic Training (Part 1 of 3) 01 Easy Ben Null Void 515 Basic Training (Part 2 of 3) 01 Easy Ben Null Void 316 Basic Training Complete 01 Easy Ben Null Void 311 Advanced Training (Part 1 of 6) 02 Normal Rex Providence HQ 500 Advanced Training (Part 2 of 6) 02 Normal Finn Providence HQ ??? Advanced Training (Part 3 of 6) 02 Normal Finn Providence HQ ??? Advanced Training (Part 4 of 6) 02 Normal Lance Providence HQ ??? Advanced Training (Part 5 of 6) 02 Normal Lance Providence HQ ??? Advanced Training (Part 6 of 6) 02 Easy Lance Providence HQ 313 Advanced Training Complete 02 Easy Lance Providence HQ 314 Meet Edd 03 Easy Computress Mt. Neverest 328 Meet Ben 03 Easy Computress Mt. Neverest 312 Meet Dexter 03 Easy Computress Mt. Neverest 329 Meet Mojo 03 Easy Computress Mt. Neverest ??? Graduated 04 Easy Computress Mt. Neverest Peach Creek Estates (The 320 Black Out Blitz* 02 Easy Mandark Future) Pokey Oaks North (The 325 Dawn of the Spawn* 02 Normal Numbuh Five Future) 317 Gum Drop* 02 Normal Numbuh 1337 Sector V (The Future) Pokey Oaks North (The 314 Map Trap* 02 Easy Buttercup Future) Pokey Oaks North (The 315 Pokey Protection* 02 Normal Buttercup Future) Pokey Oaks North (The 327 Going Places* 02 Easy Numbuh Five Future) Peach Creek Estates (The 326 Band of Bandits* 03 Normal Samurai Jack Future) 330 Candy Jarrr!* 03 Normal Licorice Lips Candy Cove (The Future) Peach Creek Commons 318 Eddy Money* 03 Normal Eddy (The -

Customer Order Form
ORDERS PREVIEWS world.com DUE th 18 FEB 2015 FEB COMIC THE SHOP’S PREVIEWSPREVIEWS CATALOG CUSTOMER ORDER FORM CUSTOMER 601 7 Feb15 Cover ROF and COF.indd 1 1/8/2015 3:45:07 PM Feb15 IFC Future Dudes Ad.indd 1 1/8/2015 9:57:57 AM FEATURED ITEMS COMIC BOOKS & GRAPHIC NOVELS The Shield #1 l ARCHIE COMIC PUBLICATIONS 1 Sonic/Mega Man: Worlds Collide: The Complete Epic TP l ARCHIE COMIC PUBLICATIONS Crossed: Badlands #75 l AVATAR PRESS INC Extinction Parade Volume 2: War TP l AVATAR PRESS INC Lady Mechanika: The Tablet of Destinies #1 l BENITEZ PRODUCTIONS UFOlogy #1 l BOOM! STUDIOS Lumberjanes Volume 1 TP l BOOM! STUDIOS 1 Masks 2 #1 l D. E./DYNAMITE ENTERTAINMENT Jungle Girl Season 3 #1 l D. E./DYNAMITE ENTERTAINMENT Uncanny Season 2 #1 l D. E./DYNAMITE ENTERTAINMENT Supermutant Magic Academy GN l DRAWN & QUARTERLY Rick & Morty #1 l ONI PRESS INC. Bloodshot Reborn #1 l VALIANT ENTERTAINMENT LLC GYO 2-in-1 Deluxe Edition HC l VIZ MEDIA LLC BOOKS Funnybooks: The Improbable Glories of the Best American Comic Books l COMICS Taschen’s The Bronze Age Of DC Comics 1970-1984 HC l COMICS Neil Gaiman: Chu’s Day at the Beach HC l NEIL GAIMAN Darth Vader & Friends HC l STAR WARS MAGAZINES Star Trek: The Official Starships Collection Special #5: Klingon Bird-of-Prey l EAGLEMOSS Ace Magazine #2 l COMICS Ultimate Spider-Man Magazine #3 l COMICS Doctor Who Special #40 l DOCTOR WHO 2 TRADING CARDS Topps 2015 Baseball Series 2 Trading Cards l TOPPS COMPANY APPAREL DC Heroes: Aquaman Navy T-Shirt l PREVIEWS EXCLUSIVE WEAR 2 DC Heroes: Harley Quinn “Cells” -

Happily Ever Ancient
HAPPILY EVER ANCIENT Visions of Antiquity for children in visual media HAPPILY EVER ANCIENT This work is subject to an International Creative Commons License Attribution- NonCommercial-ShareAlike 4.0, for a copy visit: http://creativecommons.org/licenses/by-nc-sa/4.0/ Visions of Antiquity for children in visual media First Edition, December 2020 ...still facing COVID-19. Editor: Asociación para la Investigación y la Difusión de la Arqueología Pública, JAS Arqueología Plaza de Mondariz, 6 28029 - Madrid www.jasarqueologia.es Attribution: In each chapter Cover: Jaime Almansa Sánchez, from nuptial lebetes at the National Archaeological Museum of Athens, Greece. ISBN: 978-84-16725-32-8 Depósito Legal: M-29023-2020 Printer: Service Pointwww.servicepoint.es Impreso y hecho en España - Printed and made in Spain CONTENTS INTRODUCTION: A CONTEMPORARY ANTIQUITY FOR CHILDREN AND YOUNG AUDIENCES IN FILMS AND CARTOONS Julián PELEGRÍN CAMPO 1 FAMILY LOVE AND HAPPILY MARRIAGES: REINVENTING MYTHICAL SOCIETY IN DISNEY’S HERCULES (1997) Elena DUCE PASTOR 19 OVER 5,000,000.001: ANALYZING HADES AND HIS PEOPLE IN DISNEY’S HERCULES Chiara CAPPANERA 41 FROM PLATO’S ATLANTIS TO INTERESTELLAR GATES: THE DISTORTED MYTH Irene CISNEROS ABELLÁN 61 MOANA AND MALINOWSKI: AN ANTHROPOLOGICAL APPROACH TO MODERN ANIMATION Emma PERAZZONE RIVERO 79 ANIMATING ANTIQUITY ON CHILDREN’S TELEVISION: THE VISUAL WORLDS OF ULYSSES 31 AND SAMURAI JACK Sarah MILES 95 SALPICADURAS DE MOTIVOS CLÁSICOS EN LA SERIE ONE PIECE Noelia GÓMEZ SAN JUAN 113 “WHAT A NOSE!” VISIONS OF CLEOPATRA AT THE CINEMA & TV FOR CHILDREN AND TEENAGERS Nerea TARANCÓN HUARTE 135 ONCE UPON A TIME IN MACEDON. -

Introduction
Introduction th My superhero creator is Genndy Tartakovsky, born in Russia on January 17 , 1970 to Boris and Miriam Tartakovsky. Genndy moved with his family to Italy, and from there to Chicago, Illinois. He attended Lane Technical College Prep High School, where he developed an interest in animation. He went on to pursue that interest at the California Institute of the Arts. There he met animators Craig McCracken and Bob Renzetti. His time at Cal Arts set him on his career. His first job in animation was in the country of Spain, where he worked on Batman: The Animated Series. But the decisive turning point in his career was when he was hired by the famed animation studio Hanna-Barbera, for whom Tartakovsky created his first and signature animated series, Dexter’s Laboratory, the story of a smart-alecky boy genius. Tartakovsky then served as Animation Director and Cinematographer for The Powerpuff Girls Movie, working with his good friend, the director, Craig McCracken. Nominated for several Emmy awards, The Powerpuff Girls TV series proved to be prelude to Tartakovsky’s greatest work, Samurai Jack, for which he won several Emmy and other awards. Major Works and Influences Samurai Jack is a story about a samurai warrior who experiences time travel in his effort to defeat the shape-shifting, demon wizard Aku, who had imprisoned Jack’s father. Like most superheroes, Jack has a secret identity, an identity so secret that we never discover his true name. Like most superheroes, Jack also has access to magic, in the form of his katana, a Japanese sword with special powers. -

Shounen from Samurai Dramas to Kung Fu Comedies, Shounen Manga Covers a Broad Range of What's Considered 'Men's Comics' in Japan
Recommended Reading List: Shounen From samurai dramas to kung fu comedies, shounen manga covers a broad range of what's considered 'men's comics' in Japan. But shounen manga can appeal to everyone! If you're a fan of Kurosawa movies, Japanese culture or epics, check out the manga we've gathered here. www.sequentialtart.com Blade of the Immortal Island by Hiroaki Samura by In-Wan Youn and Kyung-Il Yang Dark Horse Comics (www.darkhorse.com) TOKYOPOP (www.tokyopop.com) http://read.sequentialtart.com/?bladeoftheimmortal http://read.sequentialtart.com/?island You'll enjoy this if you like: Blade, Samurai Jack [MATURE READERS] Rin is a young woman looking to avenge the death of her You'll enjoy this if you like: Angel parents. She is joined by Manji, a ronin who has been Won Miho was bored with her life and wanted a change. cursed with immortality until he can kill one thousand evil Her father got her a job on the island of Cheju - a place men. Together, the body count rises. that looks like veritable paradise, but houses dark, unspeakable evils. When she becomes the target of Lone Wolf & Cub demons, who will save her? by Kazuo Koike, Goseki Kojima Dark Horse Comics (www.darkhorse.com) Akira http://read.sequentialtart.com/?lonewolfandcub by Katsuhiro Otomo You'll enjoy this if you like: Akira Kurosawa Dark Horse (www.darkhorse.com) During the dark days of Japan's history, this is the story http://read.sequentiatlart.com/?akira of a samurai who was once the Shogun's executioner. -

2021 February 修正版1223.Xlsx
CARTOON NETWORK February 2021 MON. -FRI. SAT. SUN. 4:00 Grizzy and the Lemmings We Bare Bears 4:00 4:30 The Powerpuff Girls BEN 10 4:30 5:00 Uncle Grandpa The Amazing World of Gumball 5:00 5:30 Sylvester & Tweety Mysteries Oggy & the Cockroaches (season 5) 5:30 6:00 Thomas and Friends 6:00 The Happos Family Season 2 6:30 6:30 Sergeant Keroro(J) Pingu in the City 6:40 7:00 7:00 Uncle Grandpa 7:30 Uncle Grandpa 7:30 8:00 Unikitty! Tom & Jerry series 8:00 8:30 Baby Looney Tunes 9:00 Tom & Jerry series The Amazing World of Gumball 9:00 9:30 Grizzy and the Lemmings 10:00 Thomas and Friends Mao Mao: Heroes of Pure Heart 10:00 10:30 The Happos Family Season 2 DC SUPER HERO GIRLS(Seson6) 10:30 10:40 Pingu in the City 11:00 Oggy & the Cockroaches (season 5) TEEN TiTANS GO! 11:00 11:30 Unikitty! Uncle Grandpa 11:30 12:00 Thomas and Friends 12:00 12:30 The Happos Family Season 2 Grizzy and the Lemmings 12:30 12:40 Pingu in the City 13:00 Dorothy and the Wizard of Oz 13:00 SHIZUKU (J) 13:30 Oggy & the Cockroaches (season 5) 13:30 14:00 Eagle Talon series (J) 14:00 SHIZUKU (J) 14:30 The Powerpuff Girls 14:30 15:00 Buck & Buddy Uncle Grandpa 15:00 15:15 Uncle Grandpa 15:30 The New Looney Tunes Show 15:30 16:00 16:00 Sergeant Keroro(J) Tom & Jerry series 16:30 16:30 17:00 17:00 Adventure Time The Amazing World of Gumball 17:30 17:30 18:00 18:00 The Amazing World of Gumball TEEN TiTANS GO! 18:30 18:30 19:00 Victor and Valentino 19:00 Tom & Jerry series 19:30 We Bare Bears 19:30 20:00 The New Looney Tunes Show 20:00 Sergeant Keroro(J) 20:30 OK KO: Let's Be Heroes! 20:30 21:00 Taffy 21:00 The Amazing World of Gumball 21:30 Oggy & the Cockroaches (season 5) 21:30 22:00 A Destructive God Sits Next to Adventure Time 22:00 Eagle Talon series(J) 22:30 Me(J) Bravest Warriors 22:30 23:00 23:00 23:30 Tom & Jerry series / The Bugs Bunny Show / MGM Cartoons 23:30 0:00 0:00 Samurai Jack remaster ver. -

Looking Back at the Creative Process
IATSE LOCAL 839 MAGAZINE SPRING 2020 ISSUE NO. 9 THE ANIMATION GUILD QUARTERLY SCOOBY-DOO / TESTING PRACTICES LOOKING BACK AT THE CREATIVE PROCESS SPRING 2020 “HAS ALL THE MAKINGS OF A CLASSIC.” TIME OUT NEW YORK “A GAMECHANGER”. INDIEWIRE NETFLIXGUILDS.COM KEYFRAME QUARTERLY MAGAZINE OF THE ANIMATION GUILD, COVER 2 REVISION 1 NETFLIX: KLAUS PUB DATE: 01/30/20 TRIM: 8.5” X 10.875” BLEED: 8.75” X 11.125” ISSUE 09 CONTENTS 12 FRAME X FRAME 42 TRIBUTE 46 FRAME X FRAME Kickstarting a Honoring those personal project who have passed 6 FROM THE 14 AFTER HOURS 44 CALENDAR FEATURES PRESIDENT Introducing The Blanketeers 46 FINAL NOTE 20 EXPANDING THE Remembering 9 EDITOR’S FIBER UNIVERSE Disney, the man NOTE 16 THE LOCAL In Trolls World Tour, Poppy MPI primer, and her crew leave their felted Staff spotlight 11 ART & CRAFT homes to meet troll tribes Tiffany Ford’s from different regions of the color blocks kingdom in an effort to thwart Queen Barb and King Thrash from destroying all the other 28 styles of music. Hitting the road gave the filmmakers an opportunity to invent worlds from the perspective of new fabrics and fibers. 28 HIRING HUMANELY Supervisors and directors in the LA animation industry discuss hiring practices, testing, and the realities of trying to staff a show ethically. 34 ZOINKS! SCOOBY-DOO TURNS 50 20 The original series has been followed by more than a dozen rebooted series and movies, and through it all, artists and animators made sure that “those meddling kids” and a cowardly canine continued to unmask villains. -

Perfect Little Feminists? Young Girls in the US Interpret Gender, Violence, and Friendship in Cartoons
University of South Carolina Scholar Commons Faculty Publications Communication Department 11-2010 Perfect Little eF minists? Young Girls in the US Interpret Gender, Violence, and Friendship in Cartoons Spring-Serenity Duvall University of South Carolina - Aiken, [email protected] Follow this and additional works at: https://scholarcommons.sc.edu/ aiken_communications_facpub Part of the Communication Commons Publication Info Postprint version. Published in Journal of Children and Media, Volume 4, Issue 4, 2010, pages 402-417. Duvall, S. (2010). Perfect little feminists? Young girls in the US interpret gender, violence, and friendship in cartoons. Journal of Children and Media, 4(4), 402-417. © Journal of Children and Media, 2010, Taylor and Francis. This is an Author's Accepted Manuscript of an article published in The Journal of Children and Media, 2010, © Taylor & Francis, available online at: http://www.tandfonline.com/10.1080/17482798.2010.510007 DOI:10.1080/17482798.2010.510007 This Article is brought to you by the Communication Department at Scholar Commons. It has been accepted for inclusion in Faculty Publications by an authorized administrator of Scholar Commons. For more information, please contact [email protected]. Perfect little feminists?: Young girls interpret gender, violence, and friendship in cartoons 1 Perfect little feminists?: Young girls in the U.S. interpret gender, violence, and friendship in cartoons Abstract Girls’ studies has emerged as a dynamic area of scholarship that examines the cultural construction of girlhood, the role that girls play in society, their identity formation, and their representation in media. This paper extends previous research by interviewing young girls about their interactions with each other as they view and interpret animated cartoons. -

Danger, Danger
FINAL-1 Sat, Apr 27, 2019 6:22:37 PM tvupdateYour Weekly Guide to TV Entertainment For the week of May 5 - 11, 2019 Emily Watson stars in “Chernobyl” INSIDE Danger, •Sports highlights Page 2 •TV Word Search Page 2 •Family Favorites Page 4 Hollywood Q&A Page14 danger • On Monday, May 6, join Soviet scientist Valery Legasov (Jared Harris, “The Terror”), nuclear physicist Ulana Khomyuk (Emily Watson, “Genius”) and head of the Bureau for Fuel and Energy of the Soviet Union Boris Shcherbina (Stellan Skarsgård, “River”), as they seek to uncover the truth behind one of the world’s worst man-made catastrophes in the premiere of “Chernobyl,” on HBO. WANTED WANTED MOTORCYCLES, SNOWMOBILES, OR ATVS To advertise here GOLD/DIAMONDS BUY SELL please call ✦ 40 years in business; A+ rating with the BBB. TRADE ✦ For the record, there is only one authentic CASH FOR GOLD, PARTS & ACCESSORIESBay 4 (978) 946-2375 Group Page Shell We Need: SALES & SERVICE Motorsports 5 x 3” Gold • Silver • Coins • Diamonds MASS. MOTORCYCLE1 x 3” We are the ORIGINAL and only AUTHENTIC INSPECTIONS CASH FOR GOLD on the Methuen line, above Enterprise Rent-A-Car 1615 SHAWSHEEN ST., TEWKSBURY, MA at 527 So. Broadway, Rte. 28, Salem, NH • 603-898-2580 978-851-3777 Open 7 Days A Week ~ www.cashforgoldinc.com WWW.BAY4MS.COM FINAL-1 Sat, Apr 27, 2019 6:22:38 PM COMCAST ADELPHIA 2 CHANNEL Kingston Sports Highlights Atkinson Londonderry 10:30 p.m. NESN Red Sox Final Live ESPN Softball NCAA ACC Tournament NESN Baseball MLB Seattle Mariners Salem Sunday Sandown Windham (60) TNT Basketball NBA Playoffs Live Women’s Championship Live at Boston Red Sox Live GUIDE Pelham, 10:55 a.m.