Downscaling Atmospheric Circulation Data for Monsoon Rainfall Forecasting in India
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

33Kv & 11Kv Tripping Information.Xlsx
33KV FEEDERS HAVING MORE THAN 5 TRIPPINGS IN LAST 3 MONTHS IN WEST DISCOM No. of 33KV Feeders No. of 33KV Feeders No. of 33KV Feeders Total No. Of 33KV S.No. Circle having more than 5 having more than 5 having more than 5 Feeders Trippings in Apr-2019 Trippings in May-2019 Trippings in June-2019 1 Indore City 75 0 2 9 2 Indore O&M 122 0 0 11 3 Khandwa 46 0 0 3 4 Burhanpur 21 0 0 0 5 Khargone 71 1 0 7 6 Barwani 33 2 0 0 7 Dhar 65 1 0 7 8 Jhabua 30 0 0 4 Indore Region 463 4 2 41 9 Ujjain 110 0 0 3 10 Dewas 102 1 2 11 11 Shajapur 59 6 0 2 12 Agar 44 0 0 2 13 Ratlam 55 0 0 8 14 Mandsaur 52 1 0 4 15 Neemuch 28 0 0 2 Ujjain Region 450 8 2 32 West Discom 913 12 4 73 11KV FEEDERS HAVING MORE THAN 8 TRIPPINGS IN LAST 3 MONTHS IN WEST DISCOM No. of 11KV Feeders having No. of 11KV Feeders having No. of 11KV Feeders having Total No. Of 11KV more than 8 Trippings in more than 8 Trippings in more than 8 Trippings in June- Feeders S.No. Circle Apr-2019 May-2019 2019 Non- Non- Non- Non- Irrigation Irrigation Irrigation Irrigation Irrigation Irrigation Total Irrigation Total Irrigation Total Feeders Feeders Feeders Feeders Feeders Feeders Feeders Feeders 1 Indore City 451 2 4 0 4 2 0 2 31 0 31 2 Indore O&M 303 304 0 0 0 0 0 0 35 12 47 3 Khandwa 168 184 2 4 6 0 2 2 25 22 47 4 Burhanpur 73 102 1 2 3 0 0 0 2 4 6 5 Khargone 218 284 0 0 0 0 0 0 2 4 6 6 Barwani 137 142 13 3 16 0 0 0 30 14 44 7 Dhar 196 347 0 2 2 1 1 2 63 37 100 8 Jhabua 182 9 0 1 1 1 0 1 45 0 45 Indore Region 1728 1374 20 12 32 4 3 7 233 93 326 9 Ujjain 314 465 3 0 3 2 0 2 28 1 29 10 Dewas 240 334 33 9 42 2 0 2 49 53 102 11 Shajapur 129 215 18 6 24 3 1 4 25 23 48 12 Agar 63 98 7 1 8 5 1 6 15 3 18 13 Ratlam 198 291 15 2 17 2 2 4 46 24 70 14 Mandsaur 226 325 21 6 27 8 3 11 61 43 104 15 Neemuch 138 196 28 14 42 10 0 10 46 46 92 Ujjain Region 1308 1924 125 38 163 32 7 39 270 193 463 West Discom 3036 3298 145 50 195 36 10 46 503 286 789 33KV Feeder wise Trippings Of MPWZ in June-2019 Total Outage Total No. -

O.I.H. Government of India Ministry of Housing & Urban Affairs Lok Sabha Unstarred Question No. 2803 to Be Answered on March
O.I.H. GOVERNMENT OF INDIA MINISTRY OF HOUSING & URBAN AFFAIRS LOK SABHA UNSTARRED QUESTION NO. 2803 TO BE ANSWERED ON MARCH 13, 2018 DEVELOPMENT OF CITIES No.2803 SHRI LAXMI NARAYAN YADAV: Will the Minister of HOUSING AND URBAN AFFAIRS be pleased to state: (a) the proposals for the development of cities forwarded by the State Government of Madhya Pradesh to the Union Government during the last three years; (b) the names of the cities and the nature of work to which the said schemes are related to; and (c) the action taken so far by the Union Government on the said proposals along with the final outcome thereof? ANSWER THE MINISTER OF STATE ((INDEPENDENT CHARGE) OF THE MINISTRY OF HOUSING & URBAN AFFAIRS (SHRI HARDEEP SINGH PURI) (a) to (c) Urban Development is a State subject. The Ministry of Housing and Urban Affairs facilitates and assists States/Union Territories (UTs), including Madhya Pradesh, in this endeavour through its various Missions- Swachh Bharat Mission (SBM), Atal Mission for Rejuvenation and Urban Transformation (AMRUT), Smart Cities Mission (SCM), Pradhan Mantri Awas Yogana(Urban)(PMAY-U) and through Metro Rail Projects to improve urban infrastructure to improve the quality of life in cities and towns covered under these Mission. List of such cities/towns in the State of Madhya Pradesh along with details of funds released are in Annexure. Under the Missions the Central Government approves the State Plans and provides the Central Assistance to the States. The projects are designed, approved and executed by the States/UTs and the Cities. Annexure Annexure referred to in reply to part (a) to (c) of Lok Sabha Unstarred Question No 2803 regarding ‘Development of Cities’ for answer on 13 March,2018 Atal Mission for Rejuvenation and Urban Transformation(AMRUT) Cities covered under AMRUT Sl.No. -

Madhya Pradesh Administrative Divisions 2011
MADHYA PRADESH ADMINISTRATIVE DIVISIONS 2011 U T KILOMETRES 40 0 40 80 120 T N Porsa ! ! ! Ater Ambah Gormi Morena ! P Bhind P A ! BHIND MORENA ! Mehgaon! A ! Ron Gohad ! Kailaras Joura Mihona Sabalgarh ! ! P ! ! Gwalior H ! Dabra Seondha ! GWALIOR ! Lahar R Beerpur Vijaypur ! ! Chinour Indergarh Bhitarwar DATIA Bhander ! T SHEOPUR Datia ! Sheopur Pohri P P P ! ! Narwar R Karahal Shivpuri A ! Karera Badoda P SHIVPURI ! S ! N!iwari D D ! ! Pichhore Orchh!a Gaurihar ! D Nowgong E ! Prithvipur Laundi Kolaras ! Chandla Jawa ! D TIKAMGARHPalera ! ! ! ! Teonthar A ! ! Jatara ! ! Maharajpur Khaniyadhana ! Sirmour Bad!arwas Mohangarh P ! Ajaigarh ! Naigarhi S ! ! Majhgawan ! REWA ! ! ! Chhatarpur Rajnagar ! Semaria ! ! Khargapur Birsinghpur Mangawan Hanumana Singoli Bamori Isagarh Chanderi ! CHHATARPUR (Raghurajnagar) ! Guna ! P Baldeogarh P Kotar (Huzur) Maugan!j Shadhora Panna P ! Raipur-Karchuliyan ! Chitrangi ! ASHOKNAGAR Tikamgarh Bijawar ! Rampur P ! J Jawad P ! ! DevendranagarNago!d !Gurh Sihawal ! ! P Baghelan ! Churhat GUNA Bada Malhera ! ! P H NEEMUCH Bhanpura Ashoknagar ! !Gunnor (Gopadbanas) ! I Raghogarh N Ghuwara D ! SATNA I ! ! A P ! Manasa ! Mungaoli PANNA Unchahara !Amarpatan Rampur Naikin Neemuch ! ! ! Amanganj SINGRAULI ! Aron ! Shahgarh Buxwaha ! Pawai SIDHI ! Kumbhraj Bina ! ! Ram!nagar !Majhauli Deosar Jiran Malhargarh Garoth Hatta ! ! Kurwai ! Shahnagar Maihar P ! ! Maksoodanga!rh Malthon Batiyagarh ! MANDSAUR ! ! ! Beohari Singrauli Mandsaur Shamgarh Jirapur ! Chachaura Lateri Sironj Khurai Raipura ! ! ! A ! P ! ! ! ! -

List of Eklavya Model Residential Schools in India (As on 20.11.2020)
List of Eklavya Model Residential Schools in India (as on 20.11.2020) Sl. Year of State District Block/ Taluka Village/ Habitation Name of the School Status No. sanction 1 Andhra Pradesh East Godavari Y. Ramavaram P. Yerragonda EMRS Y Ramavaram 1998-99 Functional 2 Andhra Pradesh SPS Nellore Kodavalur Kodavalur EMRS Kodavalur 2003-04 Functional 3 Andhra Pradesh Prakasam Dornala Dornala EMRS Dornala 2010-11 Functional 4 Andhra Pradesh Visakhapatanam Gudem Kotha Veedhi Gudem Kotha Veedhi EMRS GK Veedhi 2010-11 Functional 5 Andhra Pradesh Chittoor Buchinaidu Kandriga Kanamanambedu EMRS Kandriga 2014-15 Functional 6 Andhra Pradesh East Godavari Maredumilli Maredumilli EMRS Maredumilli 2014-15 Functional 7 Andhra Pradesh SPS Nellore Ozili Ojili EMRS Ozili 2014-15 Functional 8 Andhra Pradesh Srikakulam Meliaputti Meliaputti EMRS Meliaputti 2014-15 Functional 9 Andhra Pradesh Srikakulam Bhamini Bhamini EMRS Bhamini 2014-15 Functional 10 Andhra Pradesh Visakhapatanam Munchingi Puttu Munchingiputtu EMRS Munchigaput 2014-15 Functional 11 Andhra Pradesh Visakhapatanam Dumbriguda Dumbriguda EMRS Dumbriguda 2014-15 Functional 12 Andhra Pradesh Vizianagaram Makkuva Panasabhadra EMRS Anasabhadra 2014-15 Functional 13 Andhra Pradesh Vizianagaram Kurupam Kurupam EMRS Kurupam 2014-15 Functional 14 Andhra Pradesh Vizianagaram Pachipenta Guruvinaidupeta EMRS Kotikapenta 2014-15 Functional 15 Andhra Pradesh West Godavari Buttayagudem Buttayagudem EMRS Buttayagudem 2018-19 Functional 16 Andhra Pradesh East Godavari Chintur Kunduru EMRS Chintoor 2018-19 Functional -

List of Functional School in 2011-12 Madhya Pradesh S No. District
List of Functional School in 2011-12 Madhya Pradesh S No. District Block 1 Ashok Nagar Mungaoli 2 Ashok Nagar Eshagarh 3 Bhopal Berasia 4 Burhanpur Khaknar 5 Burhanpur Burhanpur 6 Chhatarpur Gaurihar 7 Chhatarpur Bijawar 8 Chhatarpur Buxwaha 9 Chhindwara Tamia 10 Chhindwara Amarwada 11 Chhindwara Parasia 12 Chhindwara Jamai 13 Gwalior Bhitarwar 14 Gwalior Ghatigaon 15 Harda Khirkiya 16 Hoshangabad Sohagpur 17 Hoshangabad Babai 18 Hoshangabad Bankhedi 19 Jabalpur Shahpura 20 Khandwa Harsud 21 Khandwa Pamdhana 22 Khandwa Baladi (Killod) 23 Panna Panna 24 Panna Pawai 25 Sagar Banda 26 Sagar Bina 27 Sagar Khurai 28 Sagar Malthon 29 Sagar Shahgarh 30 Vidisha Basoda 31 Vidisha Nataran 32 Vidisha Sirong 33 Vidisha Latari Alirajpur ( Jhabua Dist in 34 Alirajpur MDM List ) Bhabra(Jhabua Dist in MDM 35 Alirajpur List ) Jobat(Jhabua Dist in MDM 36 Alirajpur List ) Katthiwada(Jhabua Dist in 37 Alirajpur MDM List ) Sondwa (Jhabua Dist in MDM 38 Alirajpur List ) Udaigarh(Jhabua Dist in MDM 39 Alirajpur List ) Anuppur (SHAHDOL is in 40 Anuppur MDM list ) Jaithahri((SHAHDOL is in 41 Anuppur MDM list ) Kotma(SHAHDOL is in MDM 42 Anuppur list ) Pushaprajgarh(SHAHDOL is 43 Anuppur in MDM list ) 44 Balaghat Baihar 45 Balaghat Birsa 46 Barwani Barwani 47 Barwani Niwali 48 Barwani Pansemal 49 Barwani Pati 50 Barwani Rajpur 51 Barwani Sendhwa 52 Betul Bhimpur 53 Betul Ghoradongari 54 Betul Shahpur 55 Chhindwara Harrai 56 Damoh Tendukheda 57 Dewas Kannod 58 Dewas Khategaon 59 Dhar Badnawar 60 Dhar Bagh 61 Dhar Dahi 62 Dhar Dhar 63 Dhar Dharampuri 64 Dhar Gandhwani -

LIST of MINING PROJECTS - MPSEAC PENDING S.No
LIST OF MINING PROJECTS - MPSEAC PENDING S.No. Case No Category Name of Project Proponent Activity 1 59/2008 1(a) Agrawal Mineral process, Manganese ore mine 5.00 ha. Gwari-wadhana, 1(a) NagpurRoad , Chhindwara M.P. Teh-Sausar, Distt-Chhindwara M.P. 2 70/20081 1(a) M/s Ismail & Sons MissionChowk, Lime stone mine 10-748 ha. Village Bhatgaon (a) Katni M.P. Sunehra Teh-Murwada Katni M.P. 3 99/2008 1(a) M/s Nirmala Minerals Dubiyara Iron Ore Mine 32.375 ha. at 1(a) PathalewardKatni M.P. DubiyaraTalluka-Sihora Jabalpur M.P. 4 104/2008 1(a) Anand mining corporation Dubiyara-Tikaria Iron ore mine 26.00 ha at Village 1(a) Pathakward, Katni- M.P. Dubiyara Tikaria Jabalpur 5 411/2009 1(a) Shri Kishore Kumar Station Road , Limestone & Dolomite mine 5.605 ha. 6200 TPA 1(a) Katni-M.P. at Village- Chandan Teh- Murwara, Distt-Katni- M.P. 6 412/2009 1(a) M/s Kamal lime Industries Station Lime stone & Dolomite mine 7.205 11500 TPA at 1(a) Road Katni-M.P. Village ChandanTeh-Murwara Katni-M.P. 7 434/2009 1(a) Smt. Rekha Sharma 192, Second Laterite, clay and Red ochre deposit mine 6.83 ha. 1(a) Floor, Rachna Nagar Bhopal-M.P. at village Salebhar Teh- Bahoriband, Distt-Katni- M.P. 8 472/2009 1(a) N.M. Dubash Stone & Lime Co. Pvt Lime stone & Dolomite mine 7.42 ha. production 1(a) Ltd Station Raod, Maihar Satna capacity 1.6 lakhs TPA at village Kachhgawan, –M.P. -

Final Population Totals, Series-24
Census of India 2001 Series 24 : Madhya Pradesh FINAL POPULATION TOTALS (State, District, Tehsil and Town) Prabhal(ar Bansod Of the Indian Administrative Service Director of Census Operations, Madhya Pradesh Bhopal Websltl:: http://www.censlJsmdia.net/ © All rights reserved wIth Government of India Data Product Number 23-006-Cen-Book Preface The final population data presented in this publication IS based on the processing and tabulation of actual data captured from each and every 202 million household schedules. In the past censuses the final population totals and their basIc characteristics at the lowest geographical levels popularly known as the Village/town Primary Census Abstract was compiled manually. The generation of Primary Census Abstract for the Census 2001 is a fully computerized exercise starting from the automatic capture of data from the Household Schedule through scanning to the compilation of Primary Census Abstract. ThiS publication titled "Final Population Totals" is only a prelude to the Primary Census Abstract. The publication, which has only one table, presents data on the total population, the Scheduled Castes population and the Scheduled Tribes population by sex at the state, district, tehsll and town levels. The vitlage-wise data IS being made available In electronic format It is expected to be a useful ready reference document for data users who are only Interested to know the basic population totals. ThiS publrcatlon IS brought out by Office of the Registrar General, India (ORGI) centrally, I am happy to acknowledge the dedicated efforts of Mr Prabhakar Bansod, Director of Census Operations, Madhya Pradesh and his team and my colleagues in the ORG! in bringing out thiS publication. -
![MADHYA PRADESH BHOJ (OPEN) UNIVERSITY, BHOPAL RUN DATE: 21-Oct-2019 FINAL ROLL LIST of BA (3YDC) SECOND YEAR 2019 (OLD) [ MODE : ODL ]](https://docslib.b-cdn.net/cover/8513/madhya-pradesh-bhoj-open-university-bhopal-run-date-21-oct-2019-final-roll-list-of-ba-3ydc-second-year-2019-old-mode-odl-1388513.webp)
MADHYA PRADESH BHOJ (OPEN) UNIVERSITY, BHOPAL RUN DATE: 21-Oct-2019 FINAL ROLL LIST of BA (3YDC) SECOND YEAR 2019 (OLD) [ MODE : ODL ]
MADHYA PRADESH BHOJ (OPEN) UNIVERSITY, BHOPAL RUN DATE: 21-Oct-2019 FINAL ROLL LIST OF BA (3YDC) SECOND YEAR 2019 (OLD) [ MODE : ODL ] STUDY CENTRE : RGMMC, BAKTARA, DIST.- SEHORE (MP) (0101) REG. CENTRE : BHOPAL (01) S.No. ROLL NO NAME/S/D/W OF Sex/Catg Status Subjects 1 14010108070 SACHIN CHOUHAN/RAJESH CHOUHAN M/OBC SUPP. FC 2 15010108063 RANJEET CHOUHAN/MOHAN SINGH M/OBC SUPP. FC 3 15010108105 KIRAN KUSHWAHA/BALAKDAS F/OBC SUPP. FC 4 15010108127 MANOJ KUMAR/HARI SINGH CHOUHAN M/OBC SUPP. FC 5 16010108014 SUMIT KUMAR/DHRUV SINGH M/OBC SUPP. FC 6 16010108022 RINKI DUBEY/VISHANU PRASAD F/UR SUPP. FC 7 16010108024 POOJA SAHU/SANTOSH KUMAR F/OBC SUPP. FC 8 16010108029 DEEPA CHOUHAN/PRADEEP CHOUHAN F/OBC SUPP. FC STUDY CENTRE SUMMARY : RGMMC, BAKTARA, DIST.- SEHORE (MP) (0101) Total Fresh Suppli/ATKT EX Male Female UR OBC SC ST 8 0 8 0 4 4 1 7 0 0 ODL : OPEN AND DISTANCE LEARNING Page 1 of 220 MADHYA PRADESH BHOJ (OPEN) UNIVERSITY, BHOPAL RUN DATE: 21-Oct-2019 FINAL ROLL LIST OF BA (3YDC) SECOND YEAR 2019 (OLD) [ MODE : ODL ] STUDY CENTRE : RGMMC, MACHALPUR, DIST.- RAJGARH (MP) (0104) REG. CENTRE : BHOPAL (01) S.No. ROLL NO NAME/S/D/W OF Sex/Catg Status Subjects 1 16010408015 SANJAY RAO/RAMESH M/OBC SUPP. FC 2 16010408016 PRAKASH DANGI/RAM SINGH DANGI M/OBC SUPP. FC 3 16010408028 KAVITA KUMARI VERMA/MOHAN LAL F/SC SUPP. FC 4 16010408044 SUNIL KUMAR/JAGDISH PRASAD M/OBC SUPP. FC 5 16010408052 DEEPAK KUMAR GOUR/RAMESH CHANDRA GOUR M/OBC SUPP. -
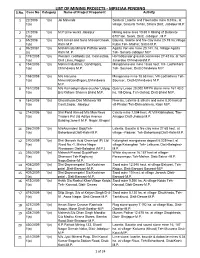
LIST of MINING PROJECTS - MPSEIAA PENDING S.No
LIST OF MINING PROJECTS - MPSEIAA PENDING S.No. Case No Category Name of Project Proponent Activity 1 22/2008 1(a) Jai Minerals Sindursi Laterite and Haematite mine 9.0 ha.. at 1(a) village, Sindursi Tehsil, Sihora Distt. Jabalpur M.P. 2 27/2008 1(a) M.P Lime works Jabalpur Mining lease area 10.60 h Mining of Dolomite 1(a) 6707 ton. Seoni, Distt. Jabalpur , M.P 3 65/2008 1(a) M/s Ismail and Sons MissionChowk, Bauxite, laterite and fire clay mine 25.19 ha.Village 1(a) Katni M.P . Kubin Teh- Maihar, Satna M.P. 4 96/20081 1(a) M/sNirmala Minaral Pathale ward- Agaria Iron ore mine 20.141. ha. Village Agaria (a) Katni M. P. Teh- Sehora Jabalpur M.P 5 119/2008 1(a) Western coalfields Ltd, Coal estate, Harradounder ground coal mines 27-45 ha. at Teh- 1(a) Civil Lines, Nagpur Junerdeo ChhindwaraM.P. 6 154/2008 1(a) Mohini Industries, Gandhiganj, Manganese ore mine 18.68 hect. Vill- Lodhikhera 1(a) Chhindwara M.P. Teh- Souncer, Distt.Chindwara M.P. 7 158/2008 1(a) M/s Haryana Manganese mine 18.68 hect. Vill-Lodhikhera Teh- 1(a) MineralsGandhiganj,Chhindwara Souncer, Distt-Chhindwara M.P. M.P. 8 161/2008 1(a) M/s Kamadigiri store crusher Udyog Quarry Lease 20,000 MTPA stone mine 161 43.0 1(a) Brij Kishore Sharma Bhind M.P. ha. Vill-Dang, Teh-Gohad, Distt-Bhind M.P. 9 184/2008 1(a) Ghanshyam Das Mahawar 95 Fireclay, Laterite & silica's and mine 8.00 hact.at 1(a) Cantt.Sadar, Jabalpur vill-Pindari Teh-Dhimarkhera, Katni M.P. -

Status of Equity Grant Scheme As on 30.10.2014 Details of the FPO's
Status of Equity Grant Scheme as on 30.10.2014 How many applications have been made for the EGS? 20 How many applications have been made for the CGF? 1 What is the status of the applications under EGS. No. of applications Received 20 Sanctioned i) Released Funds 6 ii) Due for release of funds 1 iii) Documentation awaited 1 Due Diligence report awaited 6 Due for PSC 1 PSC done 1 Under Correspondance 3 Rejected 1 20 Details of the FPO's who have applied for EGS S.No. Name of Organisation Address State Funds Status disbursed (Rs. In lakhs) 1 Ram Rahim Producer Co. Ltd. Basanti Bai Madhya Pradesh 9.55 Released and all necessary Sisodiya documents received. File Garden, Closed Bagli, District Dewas, M.P. 455227 2 Petlawad Tribal Farmer Producer Company Ltd. Thandla Madhya Pradesh 6.00 Released Road, Petlawad, Dist. Jhabua, M.P.- 457773 3 Devbhumi Natural Products Producers Co. Ltd., Plot No. Uttarakhand Due for release 15; Old SBI Lane, Mohabbew al Industrial Area, Dehradun- 248110, Uttarakhan 4 Nimad Farmers Producer Co. Ltd., Neard Jila Madhya Pradesh 8.48 Released Sahkari Bank, Julwaniya Road, Ojahr, Teh. Rajpur, Dist- Barwani, M.P.- 451449 5 Bijawar Producer Co. Ltd. Mahal Madhya Pradesh 6.10 Released Road, Near Guest House, Bijawar, M.P- 471405 6 Alirajpur Tribal farmer Producer Co. Ltd. Narmada Madhya Pradesh 1.00 Released Colony, Opposite MPEB Alirajpur Road, Jobat, Alirajpur, M.P.- 7 Ranapur Tribal Mahila Producer Co. Ltd Jawahar457990 Madhya Pradesh 5.85 Released Marg, Kalika Mata Mandir Road, Ranapur, Jhabua, 8 Patitpaban Tribal Farmer Producer Co. -
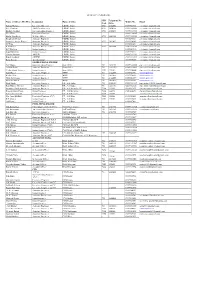
STD Telephone No
MPPKVVCL INDORE(IR) STD Telephone No. Name of Officer (Mr./Mrs.) Designation Name of Office Mobile No. Email Code Office Sanjay Mohase Executive Director ED[IR], Indore 0731 2422052 8989983763 [email protected] B.L.Chouhan Addl Chief Engineer ED[IR], Indore 0731 2424958 89899-84106 [email protected] Kishore Katthar Superintending Engineer ED[IR], Indore 0731 2424235 89899-83736 [email protected] H.A. Khan Executive Engineer ED[IR], Indore 89899-83605 [email protected] Mudit Upadhyay Welfare Officer ED[IR], Indore 0731 2423342 89899-84110 [email protected] Bhagirath Mehar Assistant Engineer ED[IR], Indore 9098674131 [email protected] Suryadev Jaydev Rasen Assistant Engineer ED[IR], Indore 0731 2421432 8989990148 [email protected] J.P.Tare Assistant Engineer ED[IR], Indore 8989983691 [email protected] P.M.Dusane Assistant Engineer (CC) ED[IR], Indore 0731 2423344 89899-83689 [email protected] K.C.Malviya Junior Engineer ED[IR], Indore 8989983840 [email protected] Kapil Bhartiya Junior Engineer ED[IR], Indore 8989990177 [email protected] Gunjan Sharma AM[HR] ED[IR], Indore 89899-91284 [email protected] Rupali Gokhale AM[HR] ED[IR], Indore 89899-91291 [email protected] Renu Pawar LawAssistant ED[IR], Indore 8989990669 [email protected] STORE CIRCLE INDORE. N.C.Gupta Superintending Engineer Store Office 731 2423111 89899-84300 [email protected] Ashish Shroff Assistant Engineer Store Office 731 2422150 89899-83813 [email protected] Mehar Singh Singaria Junior Engineer Store Office -
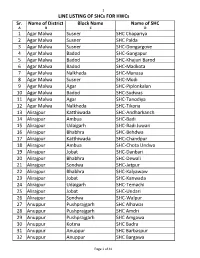
HWC-SHC Allotment List for CCCH
1 LINE LISTING OF SHCs FOR HWCs Sr. Name of District Block Name Name of SHC A B C D 1 Agar Malwa Susner SHC Chapariya 2 Agar Malwa Susner SHC Palda 3 Agar Malwa Susner SHC-Dongargove 4 Agar Malwa Badod SHC-Gangapur 5 Agar Malwa Badod SHC-Khajuri Barod 6 Agar Malwa Badod SHC-Madkota 7 Agar Malwa Nalkheda SHC-Manasa 8 Agar Malwa Susner SHC-Modi 9 Agar Malwa Agar SHC-Piplonkalan 10 Agar Malwa Badod SHC-Sudwas 11 Agar Malwa Agar SHC-Tanodiya 12 Agar Malwa Nalkheda SHC-Tikona 13 Alirajpur Katthiwada SHC-Andharkanch 14 Alirajpur Ambua SHC-Badi 15 Alirajpur Udaigarh SHC-Badi Juwari 16 Alirajpur Bhabhra SHC-Behdwa 17 Alirajpur Katthiwada SHC-Chandpur 18 Alirajpur Ambua SHC-Chota Undwa 19 Alirajpur Jobat SHC-Danbari 20 Alirajpur Bhabhra SHC-Dewali 21 Alirajpur Sondwa SHC-Jetpur 22 Alirajpur Bhabhra SHC-Kalyawaw 23 Alirajpur Jobat SHC-Kanwada 24 Alirajpur Udaigarh SHC-Temachi 25 Alirajpur Jobat SHC-Undari 26 Alirajpur Sondwa SHC-Walpur 27 Anuppur Pushprajgarh SHC Alhawar 28 Anuppur Pushprajgarh SHC Amdri 29 Anuppur Pushprajgarh SHC Amgawa 30 Anuppur Kotma SHC Badra 31 Anuppur Anuppur SHC Barbaspur 32 Anuppur Anuppur SHC Bargawa Page 1 of 41 2 LINE LISTING OF SHCs FOR HWCs Sr. Name of District Block Name Name of SHC 33 Anuppur Jaithari SHC Beend 34 Anuppur Kotma SHC Beiharbandh 35 Anuppur Pushprajgarh SHC Bilaspur 36 Anuppur Kotma SHC Chaka 37 Anuppur Jaithari SHC Choi 38 Anuppur Jaithari SHC Chorbhdhi 39 Anuppur Jaithari SHC Chulha 40 Anuppur Kotma SHC Dhangawa 41 Anuppur Pushprajgarh SHC Gonda 42 Anuppur Jaithari SHC Gorshi 43 Anuppur Anuppur