A System for Typesetting Mathematics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mandoc: Becoming the Main BSD Manual Toolbox
mandoc: becoming the main BSD manual toolbox BSDCan 2015, June 13, Ottawa Ingo Schwarze <[email protected]> Cynthia Livingston’sOTTB “Bedifferent” (c) 2013 C. Livingston (with permission) > Ingo Schwarze: mandoc page 2: INTROI BSDCan 2015, June 13, Ottawa Brief history of UNIX documentation • The key point: All documentation in one place and one format. Easy to find, uniform and easy to read and write. Be correct, complete, concise. • 1964: RUNOFF/roffmarkup syntax by Jerome H. Saltzer,MIT. Unobtrusive,diff(1)-friendly,easy to hand-edit, simple tools, high quality output. • 1971: Basic manual structure by Ken Thompson and Dennis Ritchie for the AT&T Version 1 UNIX manuals, Bell Labs. • 1979: man(7) physical markup language for AT&T Version 7 UNIX. • 1989: mdoc(7) semantic markup by Cynthia Livingston for 4.3BSD-Reno. Powerful, self-contained, portable. • 1989: GNU troffbyJames Clarke. • 2001: mdoc(7) rewrite by Werner Lemberg and Ruslan Ermilovfor groff-1.17. • 2008: mandoc(1) started by Kristaps Dzonsons. • 2010: mandoc(1) is the only documentation formatter in the OpenBSD base system. • 2014: mandoc(1) used by default in OpenBSD, FreeBSD, NetBSD, illumos. 16:19:30 What is the mandoc toolbox? → < > Ingo Schwarze: mandoc page 3: INTROIIBSDCan 2015, June 13, Ottawa What is the mandoc toolbox? User perspective:man(1), the manual viewer One comprehensive tool! Normal operation always proceeds in three steps: 1. Find one or more manuals in the file system or using a database by manual name — man(1) — or by search query — apropos(1) =man -k The result of this step can be printed out with man -w. -

Unix Programmer's Manual
There is no warranty of merchantability nor any warranty of fitness for a particu!ar purpose nor any other warranty, either expressed or imp!ied, a’s to the accuracy of the enclosed m~=:crials or a~ Io ~helr ,~.ui~::~::.j!it’/ for ~ny p~rficu~ar pur~.~o~e. ~".-~--, ....-.re: " n~ I T~ ~hone Laaorator es 8ssumg$ no rO, p::::nS,-,,.:~:y ~or their use by the recipient. Furln=,, [: ’ La:::.c:,:e?o:,os ~:’urnes no ob~ja~tjon ~o furnish 6ny a~o,~,,..n~e at ~ny k:nd v,,hetsoever, or to furnish any additional jnformstjcn or documenta’tjon. UNIX PROGRAMMER’S MANUAL F~ifth ~ K. Thompson D. M. Ritchie June, 1974 Copyright:.©d972, 1973, 1974 Bell Telephone:Laboratories, Incorporated Copyright © 1972, 1973, 1974 Bell Telephone Laboratories, Incorporated This manual was set by a Graphic Systems photo- typesetter driven by the troff formatting program operating under the UNIX system. The text of the manual was prepared using the ed text editor. PREFACE to the Fifth Edition . The number of UNIX installations is now above 50, and many more are expected. None of these has exactly the same complement of hardware or software. Therefore, at any particular installa- tion, it is quite possible that this manual will give inappropriate information. The authors are grateful to L. L. Cherry, L. A. Dimino, R. C. Haight, S. C. Johnson, B. W. Ker- nighan, M. E. Lesk, and E. N. Pinson for their contributions to the system software, and to L. E. McMahon for software and for his contributions to this manual. -

Typing Documents on the UNIX System: Using the –Ms and –Mcs
Typing Documents on the UNIX System: Using the ±ms and ±mcs Macros with Troff² L. L. Cherry M. E. Lesk AT&T Bell Laboratories Murray Hill, New Jersey 07974 ABSTRACT This document describes a set of easy-to-use macros for preparing documents on the UNIX operating system. The macros provide facilities for paragraphs, sections headings (optionally with automatic numbering), page titles, footnotes, equations, tables, two-column for- mat, and several formats of cover pages for papers. This memo includes, as an appendix, the text of ``A Guide to Preparing Documents with ±ms and ±mcs,'' which contains additional examples of features of ±ms. Introduction. This memorandum describes a package of commands to produce papers using the troff formatting program. As with other formatting programs, text is prepared interspersed with formatting commands. However, this package, which itself is written in troff commands, provides higher-level commands than those pro- vided with the basic troff program. A separate set of macros, ±mcs, produces an official AT&T style internal docu- ment cover sheet. The ±mcs macros automatically invoke the ±ms macros. Although the basic ±ms macros work with nroff, the ±mcs macros do not. Macro names were selected in ±mcs to avoid collisions with the original ±ms macros and thereby maintain backward compatibility. This document reflects the new macros. The commands available in this package are listed in Appendix A; the cover sheet commands and their order are in Appendix B. Text. Type normally, except that instead of indenting for paragraphs, place a line reading ``.PP'' before each paragraph. This will produce indenting and extra space. -

UNIX™ System V DOCUMENTER's WORKBENCH™ Volume ONE
___ALTOS _ UNIX™ SySTEM V DOCUMENTER'S WORKBENCH™ VOlUME ONE INTROduCTioN ANd TEXT FORMATTERS REfERENCE UNIX™ System V DOCUMENTER'S WORKBENCH™ Volume One ACKNOW'LBDGBMEN'rS The Altos logo, as it appears in this manual, is a registered trademark of Altos Computer Systems. DOCUMENTER IS WORKBENCH™ is a trademark of AT&T Technologies. IMPRINT@ and IMAGEN® are registered trademarks of the IMAGEN Corporation. TEKTRONIX® is a registered trademark of Tektronics, Inc. TELETYPE™ is a trademark of AT&T Teletype Corporation. TRENDATA® is a registered trademark of Trendata Corporation. UNIX™ is a tr ademark of AT &'1' Bell Labor at or ies. CONTENTS Chapter 1 DOCUMENTER'S WORKBENCH SOFTWARE Chapter 2 DOCUMENT PREPARATION APPENDIX USER REFERENCE MANUAL - i - Chapter 1 DOCUMENTER'S WORKBENCH SOFTWARE PAGE INTRODUCTION............................................... 1-1 HOW TO USE THIS BOOK. • . • . .. 1-2 I!.. 1 ,J Chapter 1 DOCUMENTER'S WORKBENCH SOFTWARE INTRODUCTION This book is the introductory volume of a set of documents that provide information about the DOCUMENTER'S WORKBENCH software on the UNIX* system. Other books in this series are: 307-151 Text Formatters Reference-provides a reference covering the text formatters nroff, troff (device independent), otroff (old troff), and sroff. 307 -152 Macro Packages Reference-provides a reference for the macro packages mm (memorandum macros), sroff/mm (mm macros for the sroff formatter), and mv (view graph macros). 307-153 Preprocessors Reference-provides a reference for the preprocessors tbl, pic, and eqn/neqn. This book is both an introduction to the DOCUMENTER'S WORKBENCH software and a DOCUMENTER'S WORKBENCH software command reference manual. Chapter 2 contains introductory material on some of the software, and the appendix provides pages describing the various commands that are part of the DOCUMENTER'S WORKBENCH software. -

History of Computing at Bell Labs
COMPUTING AT BELL LABS Kedar Namjoshi December 18, 2014 COPYRIGHT © 2013 ALCATEL-LUCENT. ALL RIGHTS RESERVED. EARLY HISTORY: COMPUTERS FROM TELEPHONE RELAYS The Bell Labs Model IV (~1946) George Stibitz Claude Shannon with “Theseus” (1950) “It can add, subtract, multiply and divide, remember answers and use A Symbolic Analysis of Relay and Switching them later …” Circuits, MIT Masters’ thesis, 1937 Boolean Logic = Relay Circuits 2 COPYRIGHT © 2013 ALCATEL-LUCENT. ALL RIGHTS RESERVED. THE BIRTH OF UNIX Unix (1970s) An explosion of creativity “Little languages” and software tools with enduring influence make awk grep lex yacc sed troff eqn S Unix (1969-71) Ken Thompson and Dennis Ritchie “… a system around which a fellowship can form.” “… the size constraint has encouraged not only economy but a certain elegance of design.” 3 COPYRIGHT © 2013 ALCATEL-LUCENT. ALL RIGHTS RESERVED. C, C++, AND S C++ (1979-83) Bjarne Stroustrup “When I joined I was basically told to “do something interesting” … ” C (1969-73) Dennis Ritchie S (1976-) John Chambers “C is quirky, flawed, and an enormous success.” “We were concerned to support serious data analysis… ” 4 COPYRIGHT © 2013 ALCATEL-LUCENT. ALL RIGHTS RESERVED. ALGORITHMS Karmarkar: Interior-Point Linear Programming (1984) Highly Influential Books Aho-Hopcroft-Ullman Garey-Johnson 5 COPYRIGHT © 2013 ALCATEL-LUCENT. ALL RIGHTS RESERVED. OFFSHOOTS Functional Programming: Standard ML of New Jersey (1989 - ) Formal Verification: SPIN and COSPAN (1980-) Distributed Operating Systems Plan 9 (1989 - ) Quantum Computing Shor, Willet, Grover (1994 - ) 6 COPYRIGHT © 2013 ALCATEL-LUCENT. ALL RIGHTS RESERVED. THE SECRET “The management principles here are that you hire bright people and you introduce them to the environment, and you give them general directions as to what sort of thing is wanted, and you give them lots of freedom. -

Domain-Specific Languages
Domain-specific languages • also called application specific languages, little languages • narrow domain of applicability • not necessarily programmable or Turing-complete – often declarative, not imperative • sometimes small enough that you could build one yourself • examples: – regular expressions – shell – XML, HTML, troff, (La)TEX, Markdown: markup langauges – SQL: database access – R: statistics – AMPL: mathematical optimization – Verilog: circuit design and verification – … Example: Markup / document preparation languages • illustrates topics of 333 in a different setting – tools – language design (good and bad); notation – evolution of software systems; maintenance – personal interest, research area for 10-20 years, heavy use in books • examples: – roff and related early formatters – nroff (Unix man command still uses it) – troff – TEX – HTML, etc. Unix document preparation: *roff • text interspersed with formatting commands on separate lines .sp 2! .in 5! This is a paragraph … • originally just ASCII output, fixed layout, singlecolumn • nroff: macros, a event mechanism for page layout (Turing complete) • troff: version of nroff for phototypesetters – adds features for size, font, precise positioning, bigger character sets – originally by Joe Ossanna (~1972); inherited by BWK ~1977 • photypesetter produces output on photographic paper or film • first high-quality output device at a reasonable price (~$15K) – predates laser printers by 5-10 years – predates Postscript (1982) by 10 years, PDF (1993) by 21 years – klunky, slow, messy, expensive media • very complex program, very complex language – language reflects many of the weirdnesses of first typesetter – macro packages make it usable by mortals for standard tasks • troff + phototypesetter enables book-quality output – Elements of Programming Style, Software Tools, K&R, … Extension to complex specialized material • mathematics – called “penalty copy” in the printing industry • tables • drawings • graphs • references • indexes • etc. -

Using Groff with the -Ms Macro Package
Using groff with the -ms MacroPackage Larry Kollar [email protected] This document describes the GNU re-implementation of the popular groff-ms macro package. The -ms macros are suitable for reports, letters, books, user manuals, and so forth. The package provides macros for coverpages, section headings, paragraphs, lists, foot- notes, pagination, and a table of contents. This document provides both tutorial and reference material. It also discusses dif- ferences from the AT&T -ms macros, both omissions and additions. 1. Introduction The original -ms macros were included with AT&T troff as well as the -man macros. While the -man package is intended for brief documents that can be read on-line as well as printed, the -ms macros are suitable for longer documents that are meant to be printed rather than read on-line. The -ms macro package included with -groff is a complete, bottom-up re-implementation. Several macros (specific to AT&T or Berkeley) are not included, while several newcommands are. See Differ- ences from AT&T -ms,later in this document, for more information. 1.1. Basic information Most number registers have a default unit of measurement. Specifying a unit explicitly does not cause anyproblems, and can avoid problems in complexsituations. The following are typical units: Unit Description iinches ccentimeters ppoints (about 1/72") vline height nwidth of a letter ‘‘n’’inthe current font mwidth of a letter ‘‘M’’inthe current font Ppica (1/6") Youset number registers by using the .nr request; for example: .nr PS 12 2v0.1, April 2001 2. General structureofan -ms document The -ms macro package expects a certain amount of structure, but not as much as packages such as -man or -mdoc. -

A System for Typesetting Mathematics
-- -- A System for Typesetting Mathematics Brian W. Kernighan and Lorinda L. Cherry Bell Laboratories Murray Hill, New Jersey 07974 ABSTRACT This paper describes the design and implementation of a system for typesetting mathemat- ics. The language has been designed to be easy to learn and to use by people (for example, secretaries and mathematical typists) who know neither mathematics nor typesetting. Experience indicates that the language can be learned in an hour or so, for it has few rules and fewer excep- tions. For typical expressions, the size and font changes, positioning, line drawing, and the like necessary to print according to mathematical conventions are all done automatically. For exam- ple, the input sum from i=0 to in®nity x sub i = pi over 2 produces ∞ π __ Σxi = i =0 2 The syntax of the language is speci®ed by a small context-free grammar; a compiler- compiler is used to make a compiler that translates this language into typesetting commands. Output may be produced on either a phototypesetter or on a terminal with forward and reverse half-line motions. The system interfaces directly with text formatting programs, so mixtures of text and mathematics may be handled simply. This paper is a revision of a paper originally published in CACM, March, 1975. 1. Introduction limits in the preceding example showed in its simplest ``Mathematics is known in the trade as form. This is carried further by dif®cult, or penalty, copy because it is slower, more b +________________ 1 dif®cult, and more expensive to set in type than any a 0 b 2 a +____________ other kind of copy normally occurring in books and 1 b +________ 3 journals.'' [1] a 2 . -
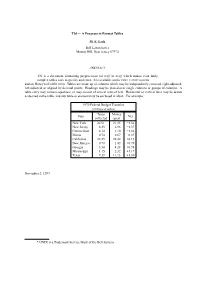
Tbl — a Program to Format Tables M. E. Lesk Bell Laboratories Murray
Tbl — A Program to Format Tables M. E. Lesk Bell Laboratories Murray Hill, New Jersey 07974 ABSTRACT Tbl is a document formatting preprocessor for troff or nroff which makes even fairly complex tables easy to specify and enter. It is available on the PDP-11 UNIX* system and on Honeywell 6000 GCOS. Tables are made up of columns which may be independently centered, right-adjusted, left-adjusted, or aligned by decimal points. Headings may be placed over single columns or groups of columns. A table entry may contain equations, or may consist of several rows of text. Horizontal or vertical lines may be drawn as desired in the table, and any table or element may be enclosed in a box. For example: 1970 Federal Budget Transfers (in billions of dollars) Taxes Money State Net collected spent New York 22.91 21.35 −1.56 New Jersey 8.33 6.96 −1.37 Connecticut 4.12 3.10 −1.02 Maine 0.74 0.67 −0.07 California 22.29 22.42 +0.13 New Mexico 0.70 1.49 +0.79 Georgia 3.30 4.28 +0.98 Mississippi 1.15 2.32 +1.17 Te xas 9.33 11.13 +1.80 November 2, 1997 * UNIX is a Trademark/Service Mark of the Bell System -- -- Tbl — A Program to Format Tables M. E. Lesk Bell Laboratories Murray Hill, New Jersey 07974 Introduction. Tbl turns a simple description of a table into a troff or nroff [1] program (list of commands) that prints the table. Tbl may be used on the PDP-11 UNIX [2] system and on the Honeywell 6000 GCOS system. -

FOREWORD the Attached Paper Appeared As Part of a Workshop Session of Tutorial Lectures Held at the PRO- TEXT I Conference in Late 1984
FOREWORD The attached paper appeared as part of a Workshop session of tutorial lectures held at the PRO- TEXT I Conference in late 1984. The lecture was an informal presentation telling the story of how the University of Nottingham equipped itself — just prior to the era of PostScript and “desk- top publishing” — to typeset all of its examination papers ‘in house’. On a personal level, my vol- unteering to lead this project triggered an interest in computerised typesetting which later devel- oped into a new direction in my computer science research interests. This ‘new direction’ has now lasted for more than 20 years and has grown to encompass almost all aspects of a subject now called ‘document engineering’. The paper is of some historical interest, if only to note that the equipment we used cost us the staggering sum of £80,000 in 1982. Nowadays comparable quality, and much greater speed, could be obtained from a computer and laser-printer combination costing about one twentieth of that amount. The key factors in the success of our project, in those very early days, were the willingness of the University not only to buy the necessary typesetters and computers but also to purchase a source code licence for the device-independent version of troff. This latter item, at £4000, was not cheap but it has done sterling service and is still in use, some 20 years later, in the School of Computer Science. Above all, the device independent troff, (unlike the original version of troff which was for the second-generation GSI CAT typesetter only) proved to be readily adaptable to a variety of typesetters and laser-printers. -

A Research UNIX Reader: Annotated Excerpts from the Programmer's
AResearch UNIX Reader: Annotated Excerpts from the Programmer’sManual, 1971-1986 M. Douglas McIlroy ABSTRACT Selected pages from the nine research editions of the UNIX®Pro grammer’sManual illustrate the development of the system. Accompanying commentary recounts some of the needs, events, and individual contributions that shaped this evolution. 1. Introduction Since it beganatthe Computing Science Research Center of AT&T Bell Laboratories in 1969, the UNIX system has exploded in coverage, in geographic distribution and, alas, in bulk. It has brought great honor to the primary contributors, Ken Thompson and Dennis Ritchie, and has reflected respect upon many others who have built on their foundation. The story of howthe system came to be and howitgrewand prospered has been told manytimes, often embroidered almost into myth. Still, aficionados seem neverto tire of hearing about howthings were in that special circle where the system first flourished. This collection of excerpts from the nine editions of the research UNIX Programmer’sManual has been chosen to illustrate trends and some of the lively give-and-take—or at least the tangible results thereof—that shaped the system. It is a domestic study,aimed only at capturing the way things were in the system’soriginal home. To look further afield would require a tome, not a report, and possibly a more dis- passionate scholar,not an intimate participant. The rawreadings are supplemented by my own recollec- tions as corrected by the memories of colleagues. The collection emphasizes development up to the Seventh Edition (v7*) in 1979, providing only occasional peeks ahead to v8 and v9. -

Making Pictures with GNU PIC
Making Pictures With GNU PIC Eric S. Raymond <[email protected]> ABSTRACT The pic language is a troff extension that makes it easy to create and alter box-and- arrowdiagrams of the kind frequently used in technical papers and textbooks. This paper is both an introduction to and reference for gpic(1), the implementation distributed by the Free Software Foundation for use with groff(1). 1. Introduction to PIC 1.1. WhyPIC? The pic language provides an easy way to write procedural box-and-arrowdiagrams to be included in troff documents. The language is sufficiently flexible to be quite useful for state charts, Petri-net diagrams, flowcharts, simple circuit schematics, jumper layouts, and other kinds of illustration involving repetitive uses of simple geometric forms and splines. Because these descriptions are procedural and object-based, theyare both compact and easy to modify. The gpic(1) implementation of pic is distributed by the Free Software Foundation for use with their groff(1) implementation of troff.Because both implementations are widely available in source form for free, theyare good bets for writing very portable documentation. 1.2. PIC Versions The original 1984 pre-ditroff(1) version of pic is long obsolete. The rewritten 1991 version is still available as part of the Documenter’sWork Bench module of System V. Where differences between Documenter’sWork Bench (1991) pic and GNU pic need to be described, original pic is referred to as "DWB pic". Details on the history of the program are givenatthe end of this document. In this document, the gpic(1) extensions will be marked as such.