FLOOD FREQUENCY ANALYSIS for KOSI RIVER at ITS BARRAGE SITE Radha Krishan1 and L.B
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Kosi Embankment Breach in Nepal: Need for a Paradigm Shift in Responding to Floods
SPECIAL ARTICLE Kosi Embankment Breach in Nepal: Need for a Paradigm Shift in Responding to Floods Ajaya Dixit The breach of the Kosi embankment in Nepal in n 18 August 2008, a flood control embankment along the August 2008 marked the failure of conventional ways Kosi River in Nepal terai breached and most of its mon- soon discharge and sediment load began flowing over an of controlling floods. After discussing the physical O area once kept flood-secure by the eastern Kosi embankment. Soon characteristics of the Kosi River and the Kosi barrage a disaster had unfolded in Sunsari district of Nepal terai and in six project, this paper suggests that the high sediment districts of north-east Bihar of India: Supaul, Madhepura, Saharsa, content of the Kosi River implies a major risk to the Arariya, Purniya and Khagariya. About 50,000 Nepalis and a stag- gering 3.5 million Indians (people of Bihar) were affected. A few proposed Kosi high dam and its ability to control floods died but the exact death toll is not known. The extent of the adverse in Bihar. It concludes by proposing the need for a effects of the widespread inundation on the dependent social and paradigm shift in dealing with the risks of floods. economic systems is only gradually becoming evident. Cloudbursts, landslides, mass movements, mud flows and flash floods are common in the mountains during the monsoon. In the plains of southern Nepal, northern Uttar Pradesh, Bihar, West Bengal and Bangladesh, rivers augmented by monsoon rains overflow their banks. Sediment eroded from the upper moun- tains is transported to the lower reaches and deposited on valleys and on the plains. -

Flood Management Strategy for Ganga Basin Through Storage
Flood Management Strategy for Ganga Basin through Storage by N. K. Mathur, N. N. Rai, P. N. Singh Central Water Commission Introduction The Ganga River basin covers the eleven States of India comprising Bihar, Jharkhand, Uttar Pradesh, Uttarakhand, West Bengal, Haryana, Rajasthan, Madhya Pradesh, Chhattisgarh, Himachal Pradesh and Delhi. The occurrence of floods in one part or the other in Ganga River basin is an annual feature during the monsoon period. About 24.2 million hectare flood prone area Present study has been carried out to understand the flood peak formation phenomenon in river Ganga and to estimate the flood storage requirements in the Ganga basin The annual flood peak data of river Ganga and its tributaries at different G&D sites of Central Water Commission has been utilised to identify the contribution of different rivers for flood peak formations in main stem of river Ganga. Drainage area map of river Ganga Important tributaries of River Ganga Southern tributaries Yamuna (347703 sq.km just before Sangam at Allahabad) Chambal (141948 sq.km), Betwa (43770 sq.km), Ken (28706 sq.km), Sind (27930 sq.km), Gambhir (25685 sq.km) Tauns (17523 sq.km) Sone (67330 sq.km) Northern Tributaries Ghaghra (132114 sq.km) Gandak (41554 sq.km) Kosi (92538 sq.km including Bagmati) Total drainage area at Farakka – 931000 sq.km Total drainage area at Patna - 725000 sq.km Total drainage area of Himalayan Ganga and Ramganga just before Sangam– 93989 sq.km River Slope between Patna and Farakka about 1:20,000 Rainfall patten in Ganga basin -

World Bank Document
Water Policy 15 (2013) 147–164 Public Disclosure Authorized Ten fundamental questions for water resources development in the Ganges: myths and realities Claudia Sadoffa,*, Nagaraja Rao Harshadeepa, Donald Blackmoreb, Xun Wuc, Anna O’Donnella, Marc Jeulandd, Sylvia Leee and Dale Whittingtonf aThe World Bank, Washington, USA *Corresponding author. E-mail: [email protected] bIndependent consultant, Canberra, Australia cNational University of Singapore, Singapore dDuke University, Durham, USA Public Disclosure Authorized eSkoll Global Threats Fund, San Francisco, USA fUniversity of North Carolina at Chapel Hill and Manchester Business School, Manchester, UK Abstract This paper summarizes the results of the Ganges Strategic Basin Assessment (SBA), a 3-year, multi-disciplinary effort undertaken by a World Bank team in cooperation with several leading regional research institutions in South Asia. It begins to fill a crucial knowledge gap, providing an initial integrated systems perspective on the major water resources planning issues facing the Ganges basin today, including some of the most important infrastructure options that have been proposed for future development. The SBA developed a set of hydrological and economic models for the Ganges system, using modern data sources and modelling techniques to assess the impact of existing and potential new hydraulic structures on flooding, hydropower, low flows, water quality and irrigation supplies at the basin scale. It also involved repeated exchanges with policy makers and opinion makers in the basin, during which perceptions of the basin Public Disclosure Authorized could be discussed and examined. The study’s findings highlight the scale and complexity of the Ganges basin. In par- ticular, they refute the broadly held view that upstream water storage, such as reservoirs in Nepal, can fully control basin- wide flooding. -

LIST of INDIAN CITIES on RIVERS (India)
List of important cities on river (India) The following is a list of the cities in India through which major rivers flow. S.No. City River State 1 Gangakhed Godavari Maharashtra 2 Agra Yamuna Uttar Pradesh 3 Ahmedabad Sabarmati Gujarat 4 At the confluence of Ganga, Yamuna and Allahabad Uttar Pradesh Saraswati 5 Ayodhya Sarayu Uttar Pradesh 6 Badrinath Alaknanda Uttarakhand 7 Banki Mahanadi Odisha 8 Cuttack Mahanadi Odisha 9 Baranagar Ganges West Bengal 10 Brahmapur Rushikulya Odisha 11 Chhatrapur Rushikulya Odisha 12 Bhagalpur Ganges Bihar 13 Kolkata Hooghly West Bengal 14 Cuttack Mahanadi Odisha 15 New Delhi Yamuna Delhi 16 Dibrugarh Brahmaputra Assam 17 Deesa Banas Gujarat 18 Ferozpur Sutlej Punjab 19 Guwahati Brahmaputra Assam 20 Haridwar Ganges Uttarakhand 21 Hyderabad Musi Telangana 22 Jabalpur Narmada Madhya Pradesh 23 Kanpur Ganges Uttar Pradesh 24 Kota Chambal Rajasthan 25 Jammu Tawi Jammu & Kashmir 26 Jaunpur Gomti Uttar Pradesh 27 Patna Ganges Bihar 28 Rajahmundry Godavari Andhra Pradesh 29 Srinagar Jhelum Jammu & Kashmir 30 Surat Tapi Gujarat 31 Varanasi Ganges Uttar Pradesh 32 Vijayawada Krishna Andhra Pradesh 33 Vadodara Vishwamitri Gujarat 1 Source – Wikipedia S.No. City River State 34 Mathura Yamuna Uttar Pradesh 35 Modasa Mazum Gujarat 36 Mirzapur Ganga Uttar Pradesh 37 Morbi Machchu Gujarat 38 Auraiya Yamuna Uttar Pradesh 39 Etawah Yamuna Uttar Pradesh 40 Bangalore Vrishabhavathi Karnataka 41 Farrukhabad Ganges Uttar Pradesh 42 Rangpo Teesta Sikkim 43 Rajkot Aji Gujarat 44 Gaya Falgu (Neeranjana) Bihar 45 Fatehgarh Ganges -

The Sediment Load of Indian Rivers — an Update
Erosion and Sediment Yield: Global and Regional Perspectives (Proceedings of the Exeter Symposium, July 1996). IAHS Publ. no. 236, 1996. 183 The sediment load of Indian rivers — an update V. SUBRAMANIAN School of Environmental Studies, Jawaharlal Nehru University, New Delhi 110 067, India Abstract This paper summarizes recent information collected on sediment transport in Indian rivers. It reveals the major contribution which Indian rivers make to the total amount of sediment delivered to the ocean at a global scale, but also highlights the large temporal and spatial variability of riverine sediment transport in the Indian sub-continent. This variability is evident not only in the quantity of the sediment transported but also in the size and mineralogical characteristics of the sediment loads. INTRODUCTION The present estimate of global sediment discharge at 15-16 X 10161 year"1 (Walling & Webb, 1983) is perhaps an underestimated value due to undetermined values for several minor catchments (Milliman &Meybeck, 1995). Nevertheless, it is now well recognized that the Pacific Oceanic islands and South and Southeast Asia constitute a single geographic region which contributes nearly 80% of the global sediment budget. Over the years, considerable data have been collected concerning sediment transport in several Indian rivers. For example, Abbas & Subramanian (1984) estimated the sediment load of the Ganges at Farraka Barrage to be 1235 t km"2 year"1, which is 8 times the world average erosion rate (1501 km“2 year"1) calculated by Milliman & Meade (1983). To improve our understanding of sediment transport processes in South Asia, there is a need to examine recently collected information. -

Constructing Reservoir Dams in Deglacierizing Regions of the Nepalese Himalaya the Geneva Challenge 2018
Constructing reservoir dams in deglacierizing regions of the Nepalese Himalaya The Geneva Challenge 2018 Submitted by: Dinesh Acharya, Paribesh Pradhan, Prabhat Joshi 2 Authors’ Note: This proposal is submitted to the Geneva Challenge 2018 by Master’s students from ETH Zürich, Switzerland. All photographs in this proposal are taken by Paribesh Pradhan in the Mount Everest region (also known as the Khumbu region), Dudh Koshi basin of Nepal. The description of the photos used in this proposal are as follows: Photo Information: 1. Cover page Dig Tsho Glacial Lake (4364 m.asl), Nepal 2. Executive summary, pp. 3 Ama Dablam and Thamserku mountain range, Nepal 3. Introduction, pp. 8 Khumbu Glacier (4900 m.asl), Mt. Everest Region, Nepal 4. Problem statement, pp. 11 A local Sherpa Yak herder near Dig Tsho Glacial Lake, Nepal 5. Proposed methodology, pp. 14 Khumbu Glacier (4900 m.asl), Mt. Everest valley, Nepal 6. The pilot project proposal, pp. 20 Dig Tsho Glacial Lake (4364 m.asl), Nepal 7. Expected output and outcomes, pp. 26 Imja Tsho Glacial Lake (5010 m.asl), Nepal 8. Conclusions, pp. 31 Thukla Pass or Dughla Pass (4572 m.asl), Nepal 9. Bibliography, pp. 33 Imja valley (4900 m.asl), Nepal [Word count: 7876] Executive Summary Climate change is one of the greatest challenges of our time. The heating of the oceans, sea level rise, ocean acidification and coral bleaching, shrinking of ice sheets, declining Arctic sea ice, glacier retreat in high mountains, changing snow cover and recurrent extreme events are all indicators of climate change caused by anthropogenic greenhouse gas effect. -

Damage from the April-May 2015 Gorkha Earthquake Sequence in the Solukhumbu District (Everest Region), Nepal David R
Damage from the april-may 2015 gorkha earthquake sequence in the Solukhumbu district (Everest region), Nepal David R. Lageson, Monique Fort, Roshan Raj Bhattarai, Mary Hubbard To cite this version: David R. Lageson, Monique Fort, Roshan Raj Bhattarai, Mary Hubbard. Damage from the april-may 2015 gorkha earthquake sequence in the Solukhumbu district (Everest region), Nepal. GSA Annual Meeting, Sep 2016, Denver, United States. hal-01373311 HAL Id: hal-01373311 https://hal.archives-ouvertes.fr/hal-01373311 Submitted on 28 Sep 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. DAMAGE FROM THE APRIL-MAY 2015 GORKHA EARTHQUAKE SEQUENCE IN THE SOLUKHUMBU DISTRICT (EVEREST REGION), NEPAL LAGESON, David R.1, FORT, Monique2, BHATTARAI, Roshan Raj3 and HUBBARD, Mary1, (1)Department of Earth Sciences, Montana State University, 226 Traphagen Hall, Bozeman, MT 59717, (2)Department of Geography, Université Paris Diderot, 75205 Paris Cedex 13, Paris, France, (3)Department of Geology, Tribhuvan University, Tri-Chandra Campus, Kathmandu, Nepal, [email protected] ABSTRACT: Rapid assessments of landslides Valley profile convexity: Earthquake-triggered mass movements (past & recent): Traditional and new construction methods: Spectrum of structural damage: (including other mass movements of rock, snow and ice) as well as human impacts were conducted by many organizations immediately following the 25 April 2015 M7.8 Gorkha earthquake and its aftershock sequence. -
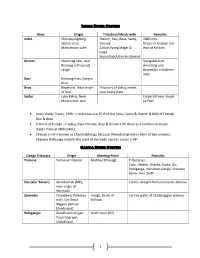
1 Indus River System River Origin Tributries/Meets with Remarks
Indus River System River Origin Tributries/Meets with Remarks Indus Chemayungdung Jhelum, Ravi, Beas, Satluj, 2880 Kms Glacier near Chenab Drains in Arabian sea Mansarovar Lake Zaskar,Syang,Shigar & east of Karachi Gilgit Shyok,Kabul,Kurram,Gomal Jhelum Sheshnag lake, near Navigable b/w Beninag in Pirpanjal Anantnag and range Baramulla in Kashmir vally Ravi Rohtang Pass, Kangra Distt. Beas Beaskund, Near origin Tributary of Satluj, meets of Ravi near Kapurthala Satluj Lake Rakas, Near Enters HP near Shipki Mansarovar lake La Pass Indus Water Treaty, 1960 :-> India can use 20 % of the Indus, Satluj & Jhelum & 80% of Chenab Ravi & Beas 5 Rivers of Punjab :-> Satluj, Ravi, Chenab, Beas & Jhelum ( All these as a combined stream meets Indus at Mithankot) Chenab in HP is known as Chandrabhanga because Chenab originate in form of two streams: Chandra & Bhanga on both the sides of the Bada Laccha La pass in HP. Ganga River System Ganga Tributary Origin Meeting Point Remarks Yamuna Yamunotri Glaciar Allahbad (Prayag) Tributaries: Tons, Hindon, Sharda, Kunta, Gir, Rishiganga, Hanuman Ganga, Chambal, Betwa, Ken, Sindh Son (aka ‘Savan’) Amarkantak (MP), Comes straight from peninsular plateau near origin of Narmada Damodar Chandawa, Palamau Hoogli, South of Carries water of Chotanagpur plateau distt. On Chota Kolkata Nagpur plateau (Jharkhand) Ramganga: Doodhatoli ranges, Ibrahimpur (UP) Pauri Gharwal, Uttrakhand 1 Gandak Nhubine Himal Glacier, Sonepur, Bihar It originates as ‘Kali Gandak’ Tibet-Mustang border Called ‘Narayani’ in Nepal nepal Bhuri Gandak Bisambharpur, West Khagaria, Bihar Champaran district Bhagmati Where three headwater streams converge at Bāghdwār above the southern edge of the Shivapuri Hills about 15 km northeast of Kathmandu Kosi near Kursela in the Formed by three main streams: the Katihar district Tamur Koshi originating from Mt. -

Journal of Integrated Disaster Risk Manangement
IDRiM(2013)3(1) ISSN: 2185-8322 DOI10.5595/idrim.2013.0061 Journal of Integrated Disaster Risk Management Original paper Determination of Threshold Runoff for Flood Warning in Nepalese Rivers 1 2 Dilip Kumar Gautam and Khadananda Dulal Received: 05/02/2013 / Accepted: 08/04/2013 / Published online: 01/06/2013 Abstract The Southern Terai plain area of Nepal is exposed to recurring floods. The floods, landslides and avalanches in Nepal cause the loss of lives of about 300 people and damage to properties worth about 626 million NPR annually. Consequently, the overall development of the country has been adversely affected. The flood risk could be significantly reduced by developing effective operational flood early warning systems. Hence, a study has been conducted to assess flood danger levels and determine the threshold runoff at forecasting stations of six major rivers of Nepal for the purpose of developing threshold-stage based operational flood early warning system. Digital elevation model data from SRTM and ASTER supplemented with measured cross-section data and HEC-RAS model was used for multiple profile analysis and inundation mapping. Different inundation scenarios were generated for a range of flood discharge at upstream boundary and flood threshold levels or runoffs have been identified for each river, thus providing the basis for developing threshold-stage based flood early warning system in these rivers. Key Words Flood, danger level, threshold runoff, hydrodynamic model, geographic information system 1. INTRODUCTION Nepal's Terai region is the part of the Ganges River basin, which is one of the most disaster-prone regions in the world. -

Ganges Strategic Basin Assessment
Public Disclosure Authorized Report No. 67668-SAS Report No. 67668-SAS Ganges Strategic Basin Assessment A Discussion of Regional Opportunities and Risks Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized GANGES STRATEGIC BASIN ASSESSMENT: A Discussion of Regional Opportunities and Risks b Report No. 67668-SAS Ganges Strategic Basin Assessment A Discussion of Regional Opportunities and Risks Ganges Strategic Basin Assessment A Discussion of Regional Opportunities and Risks World Bank South Asia Regional Report The World Bank Washington, DC iii GANGES STRATEGIC BASIN ASSESSMENT: A Discussion of Regional Opportunities and Risks Disclaimer: © 2014 The International Bank for Reconstruction and Development / The World Bank 1818 H Street NW Washington, DC 20433 Telephone: 202-473-1000 Internet: www.worldbank.org All rights reserved 1 2 3 4 14 13 12 11 This volume is a product of the staff of the International Bank for Reconstruction and Development / The World Bank. The findings, interpretations, and conclusions expressed in this volume do not necessarily reflect the views of the Executive Directors of The World Bank or the governments they represent. The World Bank does not guarantee the accuracy of the data included in this work. The boundaries, colors, denominations, and other information shown on any map in this work do not imply any judgment on part of The World Bank concerning the legal status of any territory or the endorsement or acceptance of such boundaries. Rights and Permissions The material in this publication is copyrighted. Copying and/or transmitting portions or all of this work without permission may be a violation of applicable law. -

Introduction
CHAPTER - I INTRODUCTION 1.0 Background Ministry of Water Resources, Government of India in the year 2004 decided to undertake comprehensive assessment of feasibility of linking of the rivers of the country starting with southern rivers in a fully consultative manner and to explore the feasibility of intrastate river links of the country. Accordingly, proposal for inclusion of prefeasibility / feasibility studies of intrastate links aspect in NWDA's mandate was put up for consideration in Special General Meeting of NWDA Society held on June 28, 2006 and it was decided to incorporate this function in NWDA's mandate. Finally, MoWR vide Resolution dated November 30, 2006 modified the functions of NWDA Society to include preparation of prefeasibility/feasibility studies of intrastate links. The functions of NWDA were further modified vide MoWR Resolution dated May 19, 2011 to undertake the work of preparation of Detailed Project Reports (DPRs) of intrastate links also by NWDA. Further, the Gazette notification of the enhanced mandate was issued on June 11, 2011. In the meantime, on the basis of approval conveyed by MoWR in June, 2005, NWDA requested all the State Governments to identify the intrastate link proposals in their States and send details to NWDA for their prefeasibility / feasibility studies. Bihar responded to NWDA's request vide letter No. PMC-5(IS)-01/2006-427, Patna dated May 15, 2008 and submitted their proposals. Subsequently, a meeting was held between the officers of Water Resource Department (WRD), Government of Bihar and NWDA on June 16, 2008 in Patna. In the said meeting, Government of Bihar requested NWDA to prepare the prefeasibility reports of six intrastate links out of which two were irrigation schemes. -

Geomorphological Studies and Flood Risk Assessment of Kosi River Basin Using Remote 2011-13 Sensing and Gis Techniques
Contents List of Tables ............................................................................................................................... 4 Lists of Figures ............................................................................................................................ 5 1. Introduction ........................................................................................................................ 7 1.1 General .......................................................................................................................... 7 1.2 Flood Risk Concept ....................................................................................................... 7 1.3 Background and Motivation ....................................................................................... 12 1.4 Research Questions and Objectives ............................................................................ 13 1.5 Study Area .................................................................................................................. 14 1.6 Organization of Thesis Chapters ................................................................................. 14 2. Literature Review ............................................................................................................. 16 2.1 General ........................................................................................................................ 16 2.2 Geomorphic Controls of Floods .................................................................................