DOCSLIB.ORG

Dictionary Budget: 11

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Dictionary Budget: 11 USOO7609179B2 (12) United States Patent (10) Patent No.: US 7,609,179 B2 Diaz-Gutierrez et al. (45) Date of Patent: Oct. 27, 2009 (54) METHOD FOR COMPRESSED DATAWITH (56) References Cited REDUCED DICTIONARY SIZES BY CODING U.S. PATENT DOCUMENTS VALUE PREFIXES 5,363,098 A * 1 1/1994 Antoshenkov ............... 341.95 6,518,895 B1 2/2003 Weiss et al. (75) Inventors: Pablo Diaz-Gutierrez, Granada (ES); 6,529,912 B2 * 3/2003 Satoh et al. ................. 707/101 Vijayshankar Raman, Sunnyvale, CA 7,088,271 B2 * 8/2006 Marpe et al. ................ 341,107 (US); Garret Swart, Palo Alto, CA (US) * cited by examiner Assignee: International Business Machines Primary Examiner Peguy Jean Pierre (73) (74) Attorney, Agent, or Firm—IP Authority, LLC; Ramraj Corporation, Armonk, NY (US) Soundararajan (*) Notice: Subject to any disclaimer, the term of this patent is extended or adjusted under 35 (57) ABSTRACT U.S.C. 154(b) by 0 days. The speed of dictionary based decompression is limited by the cost of accessing random values in the dictionary. If the (21) Appl. No.: 11/970,844 size of the dictionary can be limited so it fits into cache, decompression is made to be CPU bound rather than memory bound. To achieve this, a value prefix coding scheme is pre (22) Filed: Jan. 8, 2008 sented, wherein value prefixes are stored in the dictionary to get good compression from Small dictionaries. Also pre sented is an algorithm that determines the optimal entries for (65) Prior Publication Data a value prefix dictionary. Once the dictionary fits in cache, decompression speed is often limited by the cost of mispre US 2009/O174583 A1 Jul. 9, 2009 dicted branches during Huffman code processing. A novel way is presented to quantize Huffman code lengths to allow (51) Int. C. code processing to be performed with few instructions, no H03M 7/38 (2006.01) branches, and very little extra memory. Also presented is an algorithm for code length quantization that produces the opti (52) U.S. Cl. ........................................... 341/51: 341/50 mal assignment of Huffman codes and show that the adverse (58) Field of Classification Search ................... 341/50, effect of quantization on the compression ratio is quite Small. 341/106, 65, 67,78, 79 See application file for complete search history. 15 Claims, 8 Drawing Sheets Dictionary budget: 11 () ) (E Column 1 Column 2 Column 3 Column 4 U.S. Patent Oct. 27, 2009 Sheet 1 of 8 US 7,609,179 B2 Aouenbeu U.S. Patent US 7,609,179 B2 U.S. Patent Oct. 27, 2009 Sheet 3 of 8 US 7,609,179 B2 U.S. Patent Oct. 27, 2009 Sheet 4 of 8 US 7,609,179 B2 U.S. Patent Oct. 27, 2009 Sheet 5 of 8 US 7,609,179 B2 U.S. Patent Oct. 27, 2009 Sheet 6 of 8 US 7,609,179 B2 U.S. Patent Oct. 27, 2009 Sheet 7 of 8 US 7,609,179 B2 4. U.S. Patent Oct. 27, 2009 Sheet 8 of 8 US 7,609,179 B2 ?un00en?eA NHELLVdBG.OOHLÐNETTEGOO US 7,609,179 B2 1. 2 METHOD FOR COMPRESSED DATA WITH memory of the processor. The straightforward approach to REDUCED DICTIONARY SIZES BY CODING limiting the size of the dictionary is to place only a Subset of VALUE PREFIXES the values in the dictionary and to place any values missing from the dictionary directly in the input, in lined. While this BACKGROUND OF THE INVENTION simple approach improves the memory behavior, it decreases the compression ratio, making the compression far less effec 1. Field of Invention tive and decreasing the data transfer speed. This is especially The present invention relates generally to the field of true when the on-chip memory is Small. encoding. More specifically, the present invention is related Once the dictionary fits in the on-chip memory of the to a method for compressing data with reduced dictionary 10 processor, the next bottleneck in processing compressed data sizes by coding value prefixes. is caused by mispredicted branches during decompression. 2. Discussion of Related Art This occurs because traditional Huffman code processing With the success of multi-core CPUs and data parallelism executes one or more unpredictable branches for each code it in GPUs, modern processors are once again gaining process processes. A branch is unpredictable if it is taken or not taken ing capability at the same rate that they are gaining transistors. 15 with similar probability. Each mispredicted branch can take However, access to memory has not been improving as the processor dozens of cycles to recover (see, for example, quickly. This has led to a resurgence of interest in compres the paper to Sprangle et al. entitled, “Increasing processor Sion, not only because it saves disk space and network band performance by implementing deeper pipelines”). width, but because it makes good use of limited size memo The entropy coding of data was one of the founding topics ries and allows data to be transferred more efficiently through in Information theory, and Huffman's seminal work (in the the data pathways of the processor and I/O system. The focus paper entitled, “A method for the construction of minimum on using compression for increasing speed rather than capac redundancy codes') on entropy coding broke the ground for ity means that there is a new focus on the speed at which data all that followed. Huffman codes separately encode each can be decompressed. The speed of decompression is gener value as a bit string that can be compared and manipulated ally of more interest that the speed of compression because 25 independently from the rest of the data. many data items are read mostly, that is they are compressed Most work on fixed size dictionaries has been done in the and written once, but read and decompressed many times. context of online adaptive dictionary maintenance as embod A standard compression technique is dictionary coding. ied in LZ compression (see, for example, the paper to Lempel The idea is to place Some frequent values in a dictionary, and et al. entitled, “On the complexity of finite sequences”), assign them codewords, which are shorter (i.e., take fewer bits 30 where the dictionary is constantly changing in response to the to represent) than the corresponding values. Then, occur data that has been compressed so far. In LZ compression and rences of these values in a data set can be replaced by the most of its variants, the dictionary is built over a window, a codewords. This technique has been well studied and is fixed size sequence of previously scanned characters that are widely used in different forms: a common example is Huff searched during compression for repeating strings and man Coding. 35 retained during decompression to be used by the dictionary. A The drawback with this standard dictionary coding is that primary topic of interest in this field is online item replace dictionaries can get very large when the domain has many ment algorithms, which determines when to replace an exist distinct values. For example, ifa column in a database of retail ing dictionary entry with a new entry or when to change the transactions contains dates, then some dates might be much Huffman code associated with an entry. This problem has more common than others (say weekends, or days before 40 been shown to be difficult (for example, see paper to Agostino major holidays), so dictionary coding might be considered. et al. entitled, “Bounded size dictionary compression: Sck— But the number of distinct dates can run intens of thousands. completeness and nc algorithms'). However, dictionary based compression—the most com Length-limited coding is a generalization of fixed size mon and effective form of compression—has a problem when dictionaries in which codes may have lengths between 1 and running on modern processors: Compression replaces values 45 Some integer L. One of the longest lasting contributions in the on the sequentially accessed input stream with shorter codes area is the paper to Larmore et al. entitled, "A fast algorithm that have to be looked up in a dictionary. This converts cheap for optimal length-limited Huffman Codes,” which intro sequential accesses from the input stream into what is argu duces an O(nL) algorithm for computing optimal compres ably the most expensive instruction on a modern processor: a sion codes of bounded length L. In a more system-specific random read from main memory to access the value in the 50 approach described in the paper to Liddell et al. entitled, dictionary. "Length-restricted coding using modified probability distri Random reads are expensive because they generally miss butions, optimally restricts the length of compression codes in the cache, access only a small portion of the cache line, and to a size that fits in a word of the underlying architecture. Like are not amenable to pre-fetching see paper to Baer et al. An the papers to Milidiu et al. (entitled, “Efficient implementa effective on-chip preloading scheme to reduce data access 55 tion of the WARM-UP algorithm for the construction of penalty'. One load instruction can cause the processor to length-restricted prefix codes' and “In-place length-re stall for hundreds of cycles waiting for the result to arrive stricted prefix coding'), they also provide heuristics that run from memory, which, has been getting slower as CPUs have significantly faster than the algorithm, as described in the gotten faster. With simultaneous multi-threading (SMT) the paper to Larmore et al. entitled, "A fast algorithm for optimal processor can overlap its resources by running a second hard 60 length-limited Huffman Codes, while suffering little loss in ware thread while the first thread waits for the load to com compression performance.
Load more

Recommended publications
  • HARD DRIVES How Is Data Read and Stored on a Hard Drive?
    HARD DRIVES Alternatively referred to as a hard disk drive and abbreviated as HD or HDD, thehard drive is the computer's main storage media device that permanently stores all data on the computer. The hard drive was first introduced on September 13, 1956 and consists of one or more hard drive platters inside of air sealed casing. Most computer hard drives are in an internal drive bay at the front of the computer and connect to themotherboard using either ATA, SCSI, or a SATA cable and power cable. Below, is a picture of what the inside of a hard drive looks like for a desktop and laptop hard drive. As can be seen in the above picture, the desktop hard drive has six components: the head actuator, read/write actuator arm, read/write head, spindle, and platter. On the back of a hard drive is a circuit board called the disk controller. Tip: New users often confuse memory (RAM) with disk drive space. See our memory definition for a comparison between memory and storage. How is data read and stored on a hard drive? Data sent to and from the hard drive is interpreted by the disk controller, which tells the hard drive what to do and how to move the components within the drive. When the operating system needs to read or write information, it examines the hard drives File Allocation Table (FAT) to determine file location and available areas. Once this has been determined, the disk controller instructs the actuator to move the read/write arm and align the read/write head.
    [Show full text]
  • Efficient In-Memory Indexing with Generalized Prefix Trees
    Efficient In-Memory Indexing with Generalized Prefix Trees Matthias Boehm, Benjamin Schlegel, Peter Benjamin Volk, Ulrike Fischer, Dirk Habich, Wolfgang Lehner TU Dresden; Database Technology Group; Dresden, Germany Abstract: Efficient data structures for in-memory indexing gain in importance due to (1) the exponentially increasing amount of data, (2) the growing main-memory capac- ity, and (3) the gap between main-memory and CPU speed. In consequence, there are high performance demands for in-memory data structures. Such index structures are used—with minor changes—as primary or secondary indices in almost every DBMS. Typically, tree-based or hash-based structures are used, while structures based on prefix-trees (tries) are neglected in this context. For tree-based and hash-based struc- tures, the major disadvantages are inherently caused by the need for reorganization and key comparisons. In contrast, the major disadvantage of trie-based structures in terms of high memory consumption (created and accessed nodes) could be improved. In this paper, we argue for reconsidering prefix trees as in-memory index structures and we present the generalized trie, which is a prefix tree with variable prefix length for indexing arbitrary data types of fixed or variable length. The variable prefix length enables the adjustment of the trie height and its memory consumption. Further, we introduce concepts for reducing the number of created and accessed trie levels. This trie is order-preserving and has deterministic trie paths for keys, and hence, it does not require any dynamic reorganization or key comparisons. Finally, the generalized trie yields improvements compared to existing in-memory index structures, especially for skewed data.
    [Show full text]
  • Fast Binary and Multiway Prefix Searches for Packet Forwarding
    Computer Networks 51 (2007) 588–605 www.elsevier.com/locate/comnet Fast binary and multiway prefix searches for packet forwarding Yeim-Kuan Chang * Department of Computer Science and Information Engineering, National Cheng Kung University, Tainan, Taiwan, ROC Received 24 June 2005; received in revised form 24 January 2006; accepted 12 May 2006 Available online 21 June 2006 Responsible Editor: J.C. de Oliveira Abstract Backbone routers with tens-of-gigabits-per-second links are indispensable communication devices to deploy on the Inter- net. The IP lookup operation is the most critical task that must be improved in routers. In this paper, we first present a systematic method to compare prefixes of different lengths. The list of prefixes can then be sorted and stored in a sequential array, which is contrary to the linked lists used in most of trie-based structures. Next, fast binary and multiway prefix searches assisted by auxiliary prefixes are proposed. We also developed a 32-bit representation to encode the prefixes of different lengths. For the large routing tables currently available on the Internet, the proposed multiway prefix search can achieve the worst-case number of memory accesses of three and four if the sizes of the CPU cache lines are 64 bytes and 32 bytes, respectively. The IPv4 simulation results show that the proposed prefix searches outperform the existing IP lookup schemes in terms of lookup times and memory consumption. The simulations using IPv6 routing tables also show the performance advantages of the proposed binary prefix searches. We also analyze the performance of the existing lookup schemes by con- currently considering the lookup speed, the update speed, and the memory consumption.
    [Show full text]
  • Parallel-Prefix Structures for Binary and Modulo
    PARALLEL-PREFIX STRUCTURES FOR BINARY AND MODULO f2n − 1; 2n; 2n + 1g ADDERS By JUN CHEN Bachelor of Science in Information and Control Engineering Shanghai Jiao Tong University Shanghai, China 2000 Master of Science in Electrical Engineering Illinois Institute of Technology Chicago, IL, U.S.A. 2004 Submitted to the Faculty of the Graduate College of Oklahoma State University in partial fulfillment of the requirements for the Degree of DOCTOR OF PHILOSOPHY December, 2008 PARALLEL-PREFIX STRUCTURES FOR BINARY AND MODULO f2n − 1; 2n; 2n + 1g ADDERS Dissertation Approved: Dr. James E. Stine Dissertation Advisor Dr. Louis G. Johnson Dr. Sohum Sohoni Dr. Hermann G. W. Burchard Dr. A. Gordon Emslie Dean of the Graduate College ii ACKNOWLEDGMENTS First, I would like to thank my advisor, Dr. James E. Stine, for his continuous efforts on helping me with the work through a Ph.D. degree. His enthusiasm in teaching, positive thinking, along with his strong professional strengths, guided me towards the completion of this degree. My family's support is also greatly appreciated. This work cannot be done without the support from my parents Guangzhao Chen and Shengyuan Chen and sister Yu Chen. I am very proud of being able to work with Ivan, my fellow at VLSI Computer Archi- tecture Group (VCAG). Thanks also go to Johannes Grad, an alumni of Illinois Institute of Technology, who helped me much on EDA tools. Finally, I would like to thank all the committee members, Dr. Johnson, Dr. Sohoni, Dr. Burchard and Dr. Stine. Thank you all for everything you have done to help through.
    [Show full text]
  • Megabyte from Wikipedia, the Free Encyclopedia
    Megabyte From Wikipedia, the free encyclopedia The megabyte is a multiple of the unit byte for digital information storage or transmission with two different values depending on context: 1 048 576 bytes (220) generally for computer memory;[1][2] and one million bytes (106, see prefix mega-) generally for computer storage.[1][3] The IEEE Standards Board has decided that "Mega will mean 1 000 000", with exceptions allowed for the base-two meaning.[3] In rare cases, it is used to mean 1000×1024 (1 024 000) bytes.[3] It is commonly abbreviated as Mbyte or MB (compare Mb, for the megabit). Multiples of bytes Contents SI decimal prefixes Binary IEC binary prefixes Name Value usage Name Value 1 Definition (Symbol) (Symbol) 2 Examples of use 3 10 10 3 See also kilobyte (kB) 10 2 kibibyte (KiB) 2 4 References megabyte (MB) 106 220 mebibyte (MiB) 220 5 External links gigabyte (GB) 109 230 gibibyte (GiB) 230 terabyte (TB) 1012 240 tebibyte (TiB) 240 Definition petabyte (PB) 1015 250 pebibyte (PiB) 250 exabyte (EB) 1018 260 exbibyte (EiB) 260 The term "megabyte" is commonly used to mean either zettabyte (ZB) 1021 270 zebibyte (ZiB) 270 10002 bytes or 10242 bytes. This originated as yottabyte (YB) 1024 280 yobibyte (YiB) 280 compromise technical jargon for the byte multiples that needed to be expressed by the powers of 2 but lacked See also: Multiples of bits · Orders of magnitude of data a convenient name. As 1024 (210) approximates 1000 (103), roughly corresponding SI multiples began to be used for binary multiples.
    [Show full text]
  • Bits, Bytes and Digital Information
    Today’s lecture Understand the difference between analogue Bits, bytes and and digital information Convert between decimal numbers and binary digital numbers information Lecture 2 – COMPSCI111/111G SS 2018 Analogue vs digital information Encoding information Information in the real world is continuous Real world information is stored by a computer Continuous signal using numbers Weight Visual information shown 11111111111111111111111 01111111111111111111111 00001111111111111111111 Real Weight 00000011111111111111111 00000000011111111111111 44444000001111111111111 75444000000011111111111 Information stored by a computer is digital 55554401000000111111111 33367544000000011111111 Represented by discrete numbers 22283554444000000111111 99928357544000000011111 99999233657504000001111 99999983666554400000011 Weight 99999928338674400000001 shown Image Pixels 1. Give each pixel colour a number. 2. Let the computer draw the numbers as Real Weight coloured pixels (eg. black = 0). Encoding information Numbers and Computing Sound information Numbers are used to represent all information manipulated by a computer. Sound Computers use the binary number system: ― Binary values are either 0 or 1. Waveform Samples 1. Give each sample a number (height of We use the decimal number system: green box). ― 0 to 9 are decimal values. 2. Let the computer move the loudspeaker membrane according to the samples. Number Systems Positional Notation Base: Any number can be expressed as: ― Specifies the number of digits used by the system. ― Binary is base 2. ― Decimal is base 10. ∗ ∗ ⋯ ∗ Positional notation: where is the digit at position , and is the ― Describes how numbers are written. base. ⋯ Most significant digit Least significant digit Decimal Examples Storing Decimal Numbers in a Computer 657 Series of dials: 6∗10 5∗10 7∗10 ― Each dial goes from 0 to 9. Information is stored digitally: 600 50 7 657 ― Finite number of states – 10 per dial.
    [Show full text]
  • Optimizing Parallel Prefix Operations for the Fermi Architecture
    CHAPTER Optimizing Parallel Prefix Operations for the Fermi Architecture 3 Mark Harris and Michael Garland The NVIDIA Fermi GPU architecture introduces new instructions designed to facilitate basic, but important, parallel primitives on per-thread predicates, as well as instructions for manipulating and querying bits within a word. This chapter demonstrates the application of these instructions in the construction of efficient parallel algorithm primitives such as reductions, scans, and segmented scans of binary or Boolean data. 3.1 INTRODUCTION TO PARALLEL PREFIX OPERATIONS Scan (also known as parallel prefix sums), is a fundamental parallel building block that can form the basis of many efficient parallel algorithms, including sorting, computational geometry algorithms such as quickhull, and graph algorithms such as minimum spanning tree, to name just a few [1]. Given an input sequence of values A [a0,a1,a2,:::,an] D and an arbitrary binary associative operator that we denote , the scan operation produces the output sequence ⊕ S scan. ,A/ [a0,a0 a1,a0 a1 a2,:::,a0 an]. D ⊕ D ⊕ ⊕ ⊕ ⊕ ··· ⊕ This scan is inclusive because each element si has accumulated values from all elements aj where j i. A related operation is the exclusive scan, where only elements with j < i are accumulated: ≤ X exclusive scan. ,p,A/ [p,p a0,p a0 a1,:::,p an 1]. D ⊕ D ⊕ ⊕ ⊕ ⊕ ··· ⊕ − The exclusive scan operator requires an additional prefix value p, which is often assumed to be the identity value for the operator . As a concrete example, applying⊕ inclusive scan with the operator to the input sequence [3 1 7 0 4 1 6 3] produces the result [3 4 11 11 15 16 22C 25]; applying exclusive scan with prefix p 0 to the same input produces the result [0 3 4 11 11 15 16 22].
    [Show full text]
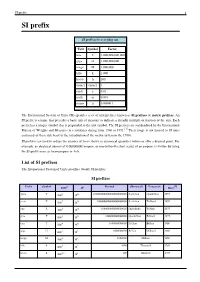
  • SI Prefix 1 SI Prefix
    SI prefix 1 SI prefix SI prefixes in everyday use Text Symbol Factor tera T 1,000,000,000,000 giga G 1,000,000,000 mega M 1,000,000 kilo k 1,000 hecto h 100 (none) (none) 1 centi c 0.01 milli m 0.001 micro μ 0.00000 1 The International System of Units (SI) specifies a set of unit prefixes known as SI prefixes or metric prefixes. An SI prefix is a name that precedes a basic unit of measure to indicate a decadic multiple or fraction of the unit. Each prefix has a unique symbol that is prepended to the unit symbol. The SI prefixes are standardized by the International Bureau of Weights and Measures in resolutions dating from 1960 to 1991.[1] Their usage is not limited to SI units and many of these date back to the introduction of the metric system in the 1790s. SI prefixes are used to reduce the number of zeros shown in numerical quantities before or after a decimal point. For example, an electrical current of 0.000000001ampere, or one-billionth (short scale) of an ampere, is written by using the SI-prefix nano as 1nanoampere or 1nA. List of SI prefixes The International System of Units specifies twenty SI prefixes: SI prefixes [2] Prefix Symbol 1000m 10n Decimal Short scale Long scale Since yotta Y 10008 1024 1000000000000000000000000 Septillion Quadrillion 1991 zetta Z 10007 1021 1000000000000000000000 Sextillion Trilliard 1991 exa E 10006 1018 1000000000000000000 Quintillion Trillion 1975 peta P 10005 1015 1000000000000000 Quadrillion Billiard 1975 tera T 10004 1012 1000000000000 Trillion Billion 1960 giga G 10003 109 1000000000 Billion
    [Show full text]
  • Memory Devices and Systems
    A-PDF Split DEMO : Purchase from www.A-PDF.com to remove the watermark CHAPTER ❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚13 ❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚❘❙❚ Memory Devices and Systems OUTLINE CHAPTER OBJECTIVES 13.1 Basic Memory Upon successful completion of this chapter, you will be able to: Concepts • Describe basic memory concepts of address and data. 13.2 Random Access • Understand how latches and flip-flops act as simple memory devices and Read/Write Memory sketch simple memory systems based on these devices. (RAM) • Distinguish between random access read/write memory (RAM) and read 13.3 Read Only Memory only memory (ROM). (ROM) • Describe the uses of tristate logic in data bussing. 13.4 Sequential Memory: • Sketch the circuits of static and dynamic RAM cells. FIFO and LIFO • Sketch a block diagram of a static or dynamic RAM chip. 13.5 Dynamic RAM Modules • Describe various types of ROM cells and arrays: mask-programmed, UV erasable, and electrically erasable. 13.6 Memory Systems • Use various types of ROM in simple applications, such as digital function generation. • Describe the basic configuration of flash memory. • Describe the basic configuration and operation of two types of sequential memory: first-in-first-out (FIFO) and last-in-first-out (LIFO). • Describe how dynamic RAM is configured into high capacity memory modules. • Sketch a basic memory system, consisting of several memory devices, an address and a data bus, and address decoding circuitry. • Represent the location of various memory device addresses on a system memory map. • Recognize and eliminate conditions leading to bus contention in a memory system. • Expand memory capacity by parallel bussing and CPLD-based decoding.
    [Show full text]
  • Units in the VO Version REC-1.0
    International Virtual Observatory Alliance Units in the VO Version REC-1.0 IVOA Recommendation 1.0 This version: http://www.ivoa.net/Documents/VOUnits/20140523/ Latest version: http://www.ivoa.net/Documents/VOUnits/ Previous versions: http://www.ivoa.net/Documents/VOUnits/20140513/ Editor(s): Sébastien Derrière and Norman Gray Authors: Markus Demleitner Sébastien Derrière Norman Gray Mireille Louys François Ochsenbein code.google.com/p/volute, rev2670, 2014-07-02 19:42:18 +0100 (Wed, 02 Jul 2014) Contents 1 Introduction (informative)6 1.1 Units in the VO Architecture..................6 1.2 Adopted terms and notations..................8 1.3 Purpose of this document....................8 1.4 What this document will not do.................9 2 The VOUnits syntax (normative) 10 2.1 String representation and encoding............... 11 2.2 Parsing unit strings – overview................. 11 2.3 Base units............................. 12 2.4 Known units........................... 12 2.5 Binary units............................ 13 2.6 Scale factors............................ 13 2.7 Astronomy symbols........................ 15 2.8 Other symbols, and other remarks............... 17 2.9 Mathematical expressions containing symbols......... 18 2.10 The numerical scale-factor.................... 19 2.11 Quoting unknown units..................... 20 2.12 General rationale (informative)................. 20 2.12.1 Deviations from other syntaxes............. 20 2.12.2 Restrictions to ASCII.................. 21 2.12.3 Other units, and unit-like expressions......... 21 3 Use cases and applications (informative) 22 3.1 Unit parsing............................ 22 3.2 Libraries.............................. 22 3.3 Unit conversion and quantity transformation.......... 23 3.4 Query languages......................... 23 3.5 Broader use in the VO...................... 24 A Current use of units (informative) 26 A.1 IAU 1989............................
    [Show full text]
  • Introduction
    “Computing is not about computers anymore. It is about living. We have seen computers move out of giant air-conditioned rooms into closets, then onto desktops, and now into our laps and pockets. But this is not the end. Like a force of nature, the digital age cannot be denied or stopped. The information superhighway may be mostly hype today, but it is an understatement about tomorrow. It will exist beyond people’s wildest predictions. We are not waiting on any invention. It is here. It is now. It is almost genetic in its nature, in that each generation will become more digital than the preceding one.” —Nicholas Negroponte, professor of media technology at MIT CHAPTER 1 Introduction 1.1 OVERVIEW r. Negroponte is among many who see the computer revolution as if it were D a force of nature. This force has the potential to carry humanity to its digi- tal destiny, allowing us to conquer problems that have eluded us for centuries, as well as all of the problems that emerge as we solve the original problems. Com- puters have freed us from the tedium of routine tasks, liberating our collective creative potential so that we can, of course, build bigger and better computers. As we observe the profound scientific and social changes that computers have brought us, it is easy to start feeling overwhelmed by the complexity of it all. This complexity, however, emanates from concepts that are fundamentally very simple. These simple ideas are the ones that have brought us to where we are today and are the foundation for the computers of the future.
    [Show full text]
  • Data Representation
    Handout 1 Data Representation Copyright c 2017 Brian Levine and Clay Shields In this handout, we are going to provide some basic information about digital systems that you need to know to understand much of the rest of the material. If you have had prior courses in computer systems, some of the topics here will be familiar. If you haven't then it might not be, but don't worry. It is not rocket science, just computer science. We are going to give you a glimpse of how computers work. We will show you what puts the \digital" in digital systems and how computers process information. We will also teach you a few principles of cryptography, which allows us to make sure that information is kept secret or unaltered. Finally, we will introduce some forensic tools so that you can use them in exercises, and on your own computer, as the course goes on. 1.1 It's All Just a Bunch of Bits A computer is a tool that processes information. We know from experience that it can handle text documents, music, video, and a wide variety of other types of files. The way that the computer handles all these disparate formats is to store them all in a common encoding that the computer can work with efficiently. This encoding, which is the native encoding of all digital devices, is called binary. In binary, everything is represented in ones and zeros, each of which is called a bit. Any number, any date, any program, any song or movie on the computer is a sequence of bits.
    [Show full text]