DOCSLIB.ORG

Theory and Applications of Monte Carlo Simulations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Theory and Applications of Monte Carlo Simulations Theory and Applications of Monte Carlo Simulations Victor (Wai Kin) Chan (Ed.) InTech, 364 pp. ISBN: 978-953-51-1012-5 The book ‘Theory and Applications of Monte Carlo Simulations’ is an excellent reference for researchers interested in exploring the full potential of Monte Carlo Simulations (MCS). The book focuses on the latest advances and applications of (MCS). It presents eleven chapters that show to which extent sampling techniques can be exploited to solve complex problems or analyze complex systems in a variety of engineering and science topics. The book explores most of the issues and topics in MCS including goodness of fit, uncertainty evaluation, variance reduction, optimization, and statistical estimation. All these concepts are extensively discussed and examples of solutions are given in order to help both researchers and practitioners. Perhaps the most valuable parts of the book are the examples of ground- breaking applications of MCS in financial systems modeling and estimation of transition behavior of organic molecules, but every single chapter teaches at least one new application or explains a useful concept about MCS. The aim of this book is to combine knowledge of MCS from diverse fields to facilitate research and new applications of MCS. Any creative researcher will be able to take advantage of the presented techniques and can find plenty of applications in their scientific field. Monte Carlo Simulations Monte Carlo simulations are an extensive class of computational algorithms that rely on repeated random sampling to obtain numerical results. One runs simulations a large number of times over in order to obtain the distribution of an unknown probabilistic entity. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to obtain a closed-form expression, or infeasible to apply a deterministic algorithm, as it also happens in medical and socioeconomic issues. Monte Carlo methods are mainly used in three distinct problem classes: optimization, numerical integration and generation of draws from a probability distribution. MCS are particularly useful in modeling phenomena with significant uncertainty in inputs such as the calculation of risk in business and evaluation of multidimensional definite integrals with complicated boundary conditions. In applications such as oil exploration problems, Monte Carlo–based predictions of failure, cost overruns and schedule overruns are routinely better than human intuition or alternative methods. The modern version of the Monte Carlo method was first applied in the late 1940s by Stanislaw Ulam, while he was working on nuclear weapons projects at the Los Alamos National Laboratory. MCS tend to follow this pattern: First a domain of possible inputs is defined, then inputs are randomly generated from a probability distribution over the domain. 45 A deterministic computation on the inputs is performed and finally the results are aggregated There is no consensus about the definition of MCS. Sawilowsky establishes a classification of three different concepts: Simulation, a Monte Carlo method, and a Monte Carlo simulation: a simulation is a representation of reality, a Monte Carlo method is a technique that can be used to solve a mathematical or statistical problem, and a Monte Carlo simulation (MCS) uses repeated sampling to determine the properties of some phenomenon or behavior. It is important to distinguish between these three concepts. An example of a simulation is to use a uniform distribution [0,1] to figure out the number of tails and heads when the number obtained is higher or lower than 0.5. A Monte Carlo method would be to toss a number of coins and compute the ratio of heads vs. tails a number of times to determine the behaviour of this variable. A MCS would be to use a large number of random uniform variables to simulate the behavior of tossing a coin. As it can be seen, these three concepts are related but they are different. MCS sample probability distribution for each variable of the system to produce a large number of possible outcomes. The results are analyzed to get probabilities of each different outcome. The main difference with traditional ‘what if’ analysis is MCS can provide samples in the very low probability regions and it makes possible a better analysis of the phenomenon under study. Thus, MCS are particularly helpful for simulating situations with considerable uncertainty in inputs and systems with a significant number of coupled degrees of freedom. Book insights The book begins with a chapter that develops a platform in Matlab that allows users to test eleven different kinds of distributions in their datasets and add new types of distributions. The correct identification of the underlying distribution is a key issue prior to data analysis and comparison with previous researches with different parameters. The Kolmogorov- Smirnov test is widely used as it is conservative but it is not always the most appropriate test. As the authors show, it is always advisable to use MCS in order to correctly identify the distribution of the data with a higher likelihood than other conventional methods. In addition to data analysis, MCS can improve the estimation of measurement uncertainties using the law of propagation of uncertainties that is based on several assumptions that are not always applicable. As chapter 2 explains the main errors are the following: There is significant non-linearity in a portion of processes that make unacceptable Taylor series analysis. The central limit is not always valid as data does not tend to a Normal distribution in all the cases. Conventional methods need to compute the degrees of freedom and sometimes this calculation is arbitrary and therefore inadequate. In this way, MCS can cope with broader problems related to uncertainties in measurement and replicate the results of other approaches for simple models. Then, their usage would be highly advisable. 46 Chapter 3 shows how MCS can be divided between exact and approximate schemes. Exact schemes capture the whole length of the sample size and the approximate methods truncate the covariance structure to obtain robust results. These schemes are applied to a specific example in a finance model but it could be easily applied to a number of models with time dependence. MCS allows computing long-range time dependence under different assumptions and makes it possible to get to the optimal result in terms of accuracy, robustness and computing speed in the case of big data being involved in the analysis. The fourth chapter presents a procedure to find robust solutions to dynamic line layout problems. This approach finds solutions that achieve minimum criteria for each scenario and estimates the form of the volume distance distribution of each parameter. Nonlinear variables are not a problem for this approach and a limited number of random samples are usually enough to reach a value sufficiently near to the global optimal solution. The sort of problems that this method is capable of solving can be unmanageable with common computational tools and it can be used in a large number of scenarios. Self-consistent event biasing schemes for MCS are also studied in the book. Three- dimensional Monte Carlo device simulator (MCDS 3-D) and the associated models/kernels such as event biasing and effective quantum potential are used in the computation of bias of subatomic particles. This method has the potential to simulate a high number of chemical, biological and social problems with a high degree of accuracy while still including the desired degree of randomness. The accuracy, precision and relative error in MCS are also commented on chapter 7. The main variable of the analysis is accuracy, but precision should also be taken into account. In most of the occasions there is a trade-off between accuracy and precision and the researcher should choose the appropriate parameters to optimize the results. The variance reduction is a main goal to achieve better results when applying MCS. Figure 1. Schematic diagram of the definition for accuracy and precision Source: Theory and Applications of Monte Carlo Simulations, page 159 47 In addition, random walk based kinetic MCS can describe diffusion and trafficking in biological systems. Each object, for example a molecule, can be randomly sampled and then the possible movements can be simulated according to predefined probabilities. The applications include complex systems of rules of cellular signaling, as extensively studied in chapter 10. The last chapter describes, with an example, how MCS is also used to differentiate tissues in medical tests that only show small differences between carcinomas and fibroglandular tissue, thus improving the diagnosis. In summary, this book is an excellent reference on the new fields of application of MCS, a highly adaptable technique that allow studying multiple problems in different areas of knowledge. The theoretical and applied examples described in the book are valuable not only to researchers in the fields of the related examples but also to any researcher in biological systems, physics, engineering and social sciences. However, this book is not a guide for beginners to MCS and previous knowledge is required to follow most of its contents. The book is published under a Creative Commons 3.0 license and is freely available at www.intechopen.com/books/theory-and-applications-of-monte-carlo-simulations By Irene Begoña Lara Universidad Autónoma de Madrid 48 .
Load more

Recommended publications
  • The Savvy Survey #16: Data Analysis and Survey Results1 Milton G
    AEC409 The Savvy Survey #16: Data Analysis and Survey Results1 Milton G. Newberry, III, Jessica L. O’Leary, and Glenn D. Israel2 Introduction In order to evaluate the effectiveness of a program, an agent or specialist may opt to survey the knowledge or Continuing the Savvy Survey Series, this fact sheet is one of attitudes of the clients attending the program. To capture three focused on working with survey data. In its most raw what participants know or feel at the end of a program, he form, the data collected from surveys do not tell much of a or she could implement a posttest questionnaire. However, story except who completed the survey, partially completed if one is curious about how much information their clients it, or did not respond at all. To truly interpret the data, it learned or how their attitudes changed after participation must be analyzed. Where does one begin the data analysis in a program, then either a pretest/posttest questionnaire process? What computer program(s) can be used to analyze or a pretest/follow-up questionnaire would need to be data? How should the data be analyzed? This publication implemented. It is important to consider realistic expecta- serves to answer these questions. tions when evaluating a program. Participants should not be expected to make a drastic change in behavior within the Extension faculty members often use surveys to explore duration of a program. Therefore, an agent should consider relevant situations when conducting needs and asset implementing a posttest/follow up questionnaire in several assessments, when planning for programs, or when waves in a specific timeframe after the program (e.g., six assessing customer satisfaction.
    [Show full text]
  • Evolution of the Infographic
    EVOLUTION OF THE INFOGRAPHIC: Then, now, and future-now. EVOLUTION People have been using images and data to tell stories for ages—long before the days of the Internet, smartphones, and Excel. In fact, the history of infographics pre-dates the web by more than 30,000 years with the earliest forms of these visuals being cave paintings that helped early humans find food, resources, and shelter. But as technology has advanced, so has our ability to tell meaningful stories. Here’s a look into the evolution of modern infographics—where they’ve been, how they’ve evolved, and where they’re headed. Then: Printed, static infographics The 20th Century introduced the infographic—a staple for how we communicate, visualize, and share information today. Early on, these print graphics married illustration and data to communicate information in a revolutionary way. ADVANTAGE Design elements enable people to quickly absorb information previously confined to long paragraphs of text. LIMITATION Static infographics didn’t allow for deeper dives into the data to explore granularities. Hoping to drill down for more detail or context? Tough luck—what you see is what you get. Source: http://www.wired.co.uk/news/archive/2012-01/16/painting- by-numbers-at-london-transport-museum INFOGRAPHICS THROUGH THE AGES DOMO 03 Now: Web-based, interactive infographics While the first wave of modern infographics made complex data more consumable, web-based, interactive infographics made data more explorable. These are everywhere today. ADVANTAGE Everyone looking to make data an asset, from executives to graphic designers, are now building interactive data stories that deliver additional context and value.
    [Show full text]
  • Using Survey Data Author: Jen Buckley and Sarah King-Hele Updated: August 2015 Version: 1
    ukdataservice.ac.uk Using survey data Author: Jen Buckley and Sarah King-Hele Updated: August 2015 Version: 1 Acknowledgement/Citation These pages are based on the following workbook, funded by the Economic and Social Research Council (ESRC). Williamson, Lee, Mark Brown, Jo Wathan, Vanessa Higgins (2013) Secondary Analysis for Social Scientists; Analysing the fear of crime using the British Crime Survey. Updated version by Sarah King-Hele. Centre for Census and Survey Research We are happy for our materials to be used and copied but request that users should: • link to our original materials instead of re-mounting our materials on your website • cite this as an original source as follows: Buckley, Jen and Sarah King-Hele (2015). Using survey data. UK Data Service, University of Essex and University of Manchester. UK Data Service – Using survey data Contents 1. Introduction 3 2. Before you start 4 2.1. Research topic and questions 4 2.2. Survey data and secondary analysis 5 2.3. Concepts and measurement 6 2.4. Change over time 8 2.5. Worksheets 9 3. Find data 10 3.1. Survey microdata 10 3.2. UK Data Service 12 3.3. Other ways to find data 14 3.4. Evaluating data 15 3.5. Tables and reports 17 3.6. Worksheets 18 4. Get started with survey data 19 4.1. Registration and access conditions 19 4.2. Download 20 4.3. Statistics packages 21 4.4. Survey weights 22 4.5. Worksheets 24 5. Data analysis 25 5.1. Types of variables 25 5.2. Variable distributions 27 5.3.
    [Show full text]
  • Monte Carlo Likelihood Inference for Missing Data Models
    MONTE CARLO LIKELIHOOD INFERENCE FOR MISSING DATA MODELS By Yun Ju Sung and Charles J. Geyer University of Washington and University of Minnesota Abbreviated title: Monte Carlo Likelihood Asymptotics We describe a Monte Carlo method to approximate the maximum likeli- hood estimate (MLE), when there are missing data and the observed data likelihood is not available in closed form. This method uses simulated missing data that are independent and identically distributed and independent of the observed data. Our Monte Carlo approximation to the MLE is a consistent and asymptotically normal estimate of the minimizer ¤ of the Kullback- Leibler information, as both a Monte Carlo sample size and an observed data sample size go to in¯nity simultaneously. Plug-in estimates of the asymptotic variance are provided for constructing con¯dence regions for ¤. We give Logit-Normal generalized linear mixed model examples, calculated using an R package that we wrote. AMS 2000 subject classi¯cations. Primary 62F12; secondary 65C05. Key words and phrases. Asymptotic theory, Monte Carlo, maximum likelihood, generalized linear mixed model, empirical process, model misspeci¯cation 1 1. Introduction. Missing data (Little and Rubin, 2002) either arise naturally|data that might have been observed are missing|or are intentionally chosen|a model includes random variables that are not observable (called latent variables or random e®ects). A mixture of normals or a generalized linear mixed model (GLMM) is an example of the latter. In either case, a model is speci¯ed for the complete data (x; y), where x is missing and y is observed, by their joint den- sity f(x; y), also called the complete data likelihood (when considered as a function of ).
    [Show full text]
  • Interactive Statistical Graphics/ When Charts Come to Life
    Titel Event, Date Author Affiliation Interactive Statistical Graphics When Charts come to Life [email protected] www.theusRus.de Telefónica Germany Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 2 www.theusRus.de What I do not talk about … Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 3 www.theusRus.de … still not what I mean. Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 4 www.theusRus.de Interactive Graphics ≠ Dynamic Graphics • Interactive Graphics … uses various interactions with the plots to change selections and parameters quickly. Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 4 www.theusRus.de Interactive Graphics ≠ Dynamic Graphics • Interactive Graphics … uses various interactions with the plots to change selections and parameters quickly. • Dynamic Graphics … uses animated / rotating plots to visualize high dimensional (continuous) data. Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 4 www.theusRus.de Interactive Graphics ≠ Dynamic Graphics • Interactive Graphics … uses various interactions with the plots to change selections and parameters quickly. • Dynamic Graphics … uses animated / rotating plots to visualize high dimensional (continuous) data. 1973 PRIM-9 Tukey et al. Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 4 www.theusRus.de Interactive Graphics ≠ Dynamic Graphics • Interactive Graphics … uses various interactions with the plots to change selections and parameters quickly. • Dynamic Graphics … uses animated / rotating plots to visualize high dimensional (continuous) data.
    [Show full text]
  • Questionnaire Analysis Using SPSS
    Questionnaire design and analysing the data using SPSS page 1 Questionnaire design. For each decision you make when designing a questionnaire there is likely to be a list of points for and against just as there is for deciding on a questionnaire as the data gathering vehicle in the first place. Before designing the questionnaire the initial driver for its design has to be the research question, what are you trying to find out. After that is established you can address the issues of how best to do it. An early decision will be to choose the method that your survey will be administered by, i.e. how it will you inflict it on your subjects. There are typically two underlying methods for conducting your survey; self-administered and interviewer administered. A self-administered survey is more adaptable in some respects, it can be written e.g. a paper questionnaire or sent by mail, email, or conducted electronically on the internet. Surveys administered by an interviewer can be done in person or over the phone, with the interviewer recording results on paper or directly onto a PC. Deciding on which is the best for you will depend upon your question and the target population. For example, if questions are personal then self-administered surveys can be a good choice. Self-administered surveys reduce the chance of bias sneaking in via the interviewer but at the expense of having the interviewer available to explain the questions. The hints and tips below about questionnaire design draw heavily on two excellent resources. SPSS Survey Tips, SPSS Inc (2008) and Guide to the Design of Questionnaires, The University of Leeds (1996).
    [Show full text]
  • STANDARDS and GUIDELINES for STATISTICAL SURVEYS September 2006
    OFFICE OF MANAGEMENT AND BUDGET STANDARDS AND GUIDELINES FOR STATISTICAL SURVEYS September 2006 Table of Contents LIST OF STANDARDS FOR STATISTICAL SURVEYS ....................................................... i INTRODUCTION......................................................................................................................... 1 SECTION 1 DEVELOPMENT OF CONCEPTS, METHODS, AND DESIGN .................. 5 Section 1.1 Survey Planning..................................................................................................... 5 Section 1.2 Survey Design........................................................................................................ 7 Section 1.3 Survey Response Rates.......................................................................................... 8 Section 1.4 Pretesting Survey Systems..................................................................................... 9 SECTION 2 COLLECTION OF DATA................................................................................... 9 Section 2.1 Developing Sampling Frames................................................................................ 9 Section 2.2 Required Notifications to Potential Survey Respondents.................................... 10 Section 2.3 Data Collection Methodology.............................................................................. 11 SECTION 3 PROCESSING AND EDITING OF DATA...................................................... 13 Section 3.1 Data Editing ........................................................................................................
    [Show full text]
  • Improving Critical Thinking Through Data Analysis*
    Midwest Manufacturing Accounting Conference Improving Critical Thinking Through Data Analysis* Kurt Reding May 17, 2018 *This presentation is based on the article, “Improving Critical Thinking Through Data Analysis,” published in the June 2017 issue of Strategic Finance. Outline . Critical thinking . Diagnostic data analysis . Merging critical thinking with diagnostic data analysis 2 Critical Thinking . “Bosses Seek ‘Critical Thinking,’ but What Is That?” (emphasis added) “It’s one of those words—like diversity was, like big data is— where everyone talks about it but there are 50 different ways to define it,” says Dan Black, Americas director of recruiting at the accounting firm and consultancy EY. (emphasis added) “Critical thinking may be similar to U.S. Supreme Court Justice Porter Stewart’s famous threshold for obscenity: You know it when you see it,” says Jerry Houser, associate dean and director of career services at Williamette University in Salem, Ore. (emphasis added) http://www.wsj.com/articles/bosses-seek-critical-thinking-but-what-is-that-1413923730 3 Critical Thinking . Critical thinking is not… − Going-through-the-motions thinking. − Quick thinking. 4 Critical Thinking . Proposed definition: Critical thinking is a manner of thinking that employs curiosity, creativity, skepticism, analysis, and logic, where: − Curiosity means wanting to learn, − Creativity means viewing information from multiple perspectives, − Skepticism means maintaining a ‘trust but verify’ mindset; − Analysis means systematically examining and evaluating evidence, and − Logic means reaching well-founded conclusions. 5 Critical Thinking . Although some people are innately more curious, creative, and/or skeptical than others, everyone can exercise these personal attributes to some degree. Likewise, while some people are naturally better analytical and logical thinkers, everyone can improve these skills through practice, education, and training.
    [Show full text]
  • Data Visualization in Exploratory Data Analysis: an Overview Of
    DATA VISUALIZATION IN EXPLORATORY DATA ANALYSIS: AN OVERVIEW OF METHODS AND TECHNOLOGIES by YINGSEN MAO Presented to the Faculty of the Graduate School of The University of Texas at Arlington in Partial Fulfillment of the Requirements for the Degree of MASTER OF SCIENCE IN INFORMATION SYSTEMS THE UNIVERSITY OF TEXAS AT ARLINGTON December 2015 Copyright © by YINGSEN MAO 2015 All Rights Reserved ii Acknowledgements First I would like to express my deepest gratitude to my thesis advisor, Dr. Sikora. I came to know Dr. Sikora in his data mining course in Fall 2013. I knew little about data mining before taking this course and it is this course that aroused my great interest in data mining, which made me continue to pursue knowledge in related field. In Spring 2015, I transferred to thesis track and I appreciated Dr. Sikora’s acceptance to be my thesis adviser, which made my academic research possible. Because this is my first time diving myself into academic research, I’m thankful for Dr. Sikora for his valuable guidance and patience throughout the thesis. Without his precious support this thesis would not have been possible. I also would like to thank the members of my Master committee, Dr. Wang and Dr. Zhang, for their insightful advices, and the kind acceptance for being my committee members at the last moment. November 17, 2015 iii Abstract DATA VISUALIZATION IN EXPLORATORY DATA ANALYSIS: AN OVERVIEW OF METHODS AND TECHNOLOGIES Yingsen Mao, MS The University of Texas at Arlington, 2015 Supervising Professor: Riyaz Sikora Exploratory data analysis (EDA) refers to an iterative process through which analysts constantly ‘ask questions’ and extract knowledge from data.
    [Show full text]
  • Exploratory Data Analysis
    Copyright © 2011 SAGE Publications. Not for sale, reproduction, or distribution. 530 Data Analysis, Exploratory The ultimate quantitative extreme in textual data Klingemann, H.-D., Volkens, A., Bara, J., Budge, I., & analysis uses scaling procedures borrowed from McDonald, M. (2006). Mapping policy preferences II: item response theory methods developed originally Estimates for parties, electors, and governments in in psychometrics. Both Jon Slapin and Sven-Oliver Eastern Europe, European Union and OECD Proksch’s Poisson scaling model and Burt Monroe 1990–2003. Oxford, UK: Oxford University Press. and Ko Maeda’s similar scaling method assume Laver, M., Benoit, K., & Garry, J. (2003). Extracting that word frequencies are generated by a probabi- policy positions from political texts using words as listic function driven by the author’s position on data. American Political Science Review, 97(2), some latent scale of interest and can be used to 311–331. estimate those latent positions relative to the posi- Leites, N., Bernaut, E., & Garthoff, R. L. (1951). Politburo images of Stalin. World Politics, 3, 317–339. tions of other texts. Such methods may be applied Monroe, B., & Maeda, K. (2004). Talk’s cheap: Text- to word frequency matrixes constructed from texts based estimation of rhetorical ideal-points (Working with no human decision making of any kind. The Paper). Lansing: Michigan State University. disadvantage is that while the scaled estimates Slapin, J. B., & Proksch, S.-O. (2008). A scaling model resulting from the procedure represent relative dif- for estimating time-series party positions from texts. ferences between texts, they must be interpreted if a American Journal of Political Science, 52(3), 705–722.
    [Show full text]
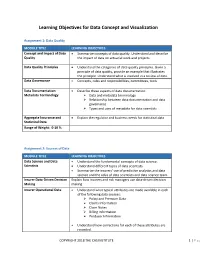
  • Learning Objectives for Data Concept and Visualization
    Learning Objectives for Data Concept and Visualization Assignment 1: Data Quality MODULE TITLE LEARNING OBJECTIVES Concept and Impact of Data • Summarize concepts of data quality. Understand and describe Quality the impact of data on actuarial work and projects. Data Quality Principles • Understand the categories of data quality principles. Given a principle of data quality, provide an example that illustrates the principle. Understand what is involved in a review of data. Data Governance • Concepts, roles and responsibilities, committees, tools Data Documentation: • Describe these aspects of data documentation: Metadata Terminology Data and metadata terminology Relationship between data documentation and data governance Types and uses of metadata for data scientists Aggregate Insurance and • Explain the regulator and business needs for statistical data Statistical Data Range of Weight: 0-10 % Assignment 2: Sources of Data MODULE TITLE LEARNING OBJECTIVES Data Science and Data • Understand the fundamental concepts of data science. Scientists • Understand different types of data scientists. • Summarize the insurers’ use of predictive analytics and data science and the roles of data scientists and data science team. Insurer Data-Driven Decision Explain how insurers and risk managers use data-driven decision Making making Insurer Operational Data • Understand what typical attributes are made available in each of the following data sources: Policy and Premium Data Claims Information Claim Notes Billing Information Producer Information • Understand how corrections for each of these attributes are recorded. COPYRIGHT 2018 THE CAS INSTITUTE 1 | Pag • Understand timing of collection and updating. Understand how quality can change over time. The Value of Statistical Plan • Understand why insurance companies produce statistical files, Data typical attributes in stat files and the advantages and disadvantages of using stat files over operational data.
    [Show full text]
  • Statistical Graphics Considerations January 7, 2020
    Statistical Graphics Considerations January 7, 2020 https://opr.princeton.edu/workshops/65 Instructor: Dawn Koffman, Statistical Programmer Office of Population Research (OPR) Princeton University 1 Statistical Graphics Considerations Why this topic? “Most of us use a computer to write, but we would never characterize a Nobel prize winning writer as being highly skilled at using a word processing tool. Similarly, advanced skills with graphing languages/packages/tools won’t necessarily lead to effective communication of numerical data. You must understand the principles of effective graphs in addition to the mechanics.” Jennifer Bryan, Associate Professor Statistics & Michael Smith Labs, Univ. of British Columbia. http://stat545‐ubc.github.io/block015_graph‐dos‐donts.html 2 “... quantitative visualization is a core feature of scientific practice from start to finish. All aspects of the research process from the initial exploration of data to the effective presentation of a polished argument can benefit from good graphical habits. ... the dominant trend is toward a world where the visualization of data and results is a routine part of what it means to do science.” But ... for some odd reason “ ... the standards for publishable graphical material vary wildy between and even within articles – far more than the standards for data analysis, prose and argument. Variation is to be expected, but the absence of consistency in elements as simple as axis labeling, gridlines or legends is striking.” 3 Kieran Healy and James Moody, Data Visualization in Sociology, Annu. Rev. Sociol. 2014 40:5.1‐5.5. What is a statistical graph? “A statistical graph is a visual representation of statistical data.
    [Show full text]