Forecasting Serve Performance in Professional Tennis Matches
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ADCTF Annual Report 2018
THE AUSTRALIAN DAVIS CUP 2018 TENNIS FOUNDATION ANNUAL ABN 90 004 905 060 Approved by Tennis Australia REPORT THE AUSTRALIAN DAVIS CUP TENNIS FOUNDATION Annual Report 2018 1 THE AUSTRALIAN DAVIS CUP TENNIS FOUNDATION Annual Report 2018 2 THE AUSTRALIAN DAVIS CUP TENNIS FOUNDATION ABN 90 004 905 060 NOTICE OF ANNUAL GENERAL MEETING Notice is hereby given that the forty-seventh Annual General Meeting of The Australian Davis Cup Tennis Foundation will be held in the Clubhouse of the Royal South Yarra Lawn Tennis Club, Williams Road North, Toorak, on Tuesday 27th November 2018 at 8.00pm. BUSINESS 1. To receive, consider and if thought fit, to adopt the Directors' Report, the Directors' Declaration, the Statement of Financial Position as at 30th June 2018, the Statement of Comprehensive Income, the Statement of Cash Flows and the Statement of Changes in Equity for the year ended 30th June 2018 together with the Auditor's Report thereon. 2. To elect four (4) Directors to replace those persons retiring in accordance with the Constitution. 3. To transact any other business that, being lawfully brought forward, is accepted by the Chairman for discussion. BY ORDER OF THE BOARD Alan J Cobb. Honorary Secretary. Melbourne, 1st October, 2018 THE AUSTRALIAN DAVIS CUP TENNIS FOUNDATION Annual Report 2018 1 PROXIES A Member entitled to attend and vote at the Meeting is entitled to appoint one proxy to attend and vote in his or her stead. A proxy must be a Member. The form for the appointment of a proxy is available on application to the Honorary Secretary and must be lodged with the Honorary Secretary no later than 48 hours prior to the scheduled commencement of the Meeting. -

ATP Challenger Tour by the Numbers
ATP MEDIA INFORMATION Updated: 20 September 2021 2021 ATP CHALLENGER BY THE NUMBERS Match Wins Leaders W-L Titles 1) Benjamin Bonzi FRA 49-11 6 2) Tomas Martin Etcheverry ARG 38-13 2 3) Zdenek Kolar CZE 29-18 3 4) Holger Rune DEN 28-7 3 5) Kacper Zuk POL 26-11 1 Nicolas Jarry CHI 26-12 1 7) Sebastian Baez ARG 25-5 3 Altug Celikbilek TUR 25-10 2 Juan Manuel Cerundolo ARG 25-10 3 Tomas Barrios Vera CHI 25-11 1 11) Jenson Brooksby USA 23-3 3 Gastao Elias POR 23-12 1 Win Percentage Leaders W-L Pct. Titles 1) Jenson Brooksby USA 23-3 88.5 3 2) Sebastian Baez ARG 25-5 83.3 3 3) Benjamin Bonzi FRA 49-11 81.7 6 4) Holger Rune DEN 28-7 80.0 3 5) Zizou Bergs BEL 19-6 76.0 3 6) Federico Coria ARG 18-6 75.0 1 7) Tomas Martin Etcheverry ARG 38-13 74.5 2 8) Arthur Rinderknech FRA 18-7 72.0 1 Botic van de Zandschulp NED 18-7 72.0 0 *Minimum 20 matches played* Singles Title Leaders ----- By Surface ----- Player Total Clay Grass Hard Carpet Benjamin Bonzi FRA 6 1 5 Sebastian Baez ARG 3 3 Zizou Bergs BEL 3 1 2 Jenson Brooksby USA 3 1 2 Juan Manuel Cerundolo ARG 3 3 Tallon Griekspoor NED 3 3 Zdenek Kolar CZE 3 3 Holger Rune DEN 3 3 Franco Agamenone ITA 2 2 Daniel Altmaier GER 2 2 Altug Celikbilek TUR 2 2 Mitchell Krueger USA 2 2 Tomas Martin Etcheverry ARG 2 2 Mats Moraing GER 2 2 Carlos Taberner ESP 2 2 Bernabe Zapata Miralles ESP 2 2 53 tied with 1 title each Winners by Age: 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 0 0 6 7 8 4 7 10 13 13 4 3 7 5 3 1 0 3 0 1 0 1 0 0 Youngest Final: Juan Manuel Cerundolo (19) d. -

Doubles Final (Seed)
2016 ATP TOURNAMENT & GRAND SLAM FINALS START DAY TOURNAMENT SINGLES FINAL (SEED) DOUBLES FINAL (SEED) 4-Jan Brisbane International presented by Suncorp (H) Brisbane $404780 4 Milos Raonic d. 2 Roger Federer 6-4 6-4 2 Kontinen-Peers d. WC Duckworth-Guccione 7-6 (4) 6-1 4-Jan Aircel Chennai Open (H) Chennai $425535 1 Stan Wawrinka d. 8 Borna Coric 6-3 7-5 3 Marach-F Martin d. Krajicek-Paire 6-3 7-5 4-Jan Qatar ExxonMobil Open (H) Doha $1189605 1 Novak Djokovic d. 1 Rafael Nadal 6-1 6-2 3 Lopez-Lopez d. 4 Petzschner-Peya 6-4 6-3 11-Jan ASB Classic (H) Auckland $463520 8 Roberto Bautista Agut d. Jack Sock 6-1 1-0 RET Pavic-Venus d. 4 Butorac-Lipsky 7-5 6-4 11-Jan Apia International Sydney (H) Sydney $404780 3 Viktor Troicki d. 4 Grigor Dimitrov 2-6 6-1 7-6 (7) J Murray-Soares d. 4 Bopanna-Mergea 6-3 7-6 (6) 18-Jan Australian Open (H) Melbourne A$19703000 1 Novak Djokovic d. 2 Andy Murray 6-1 7-5 7-6 (3) 7 J Murray-Soares d. Nestor-Stepanek 2-6 6-4 7-5 1-Feb Open Sud de France (IH) Montpellier €463520 1 Richard Gasquet d. 3 Paul-Henri Mathieu 7-5 6-4 2 Pavic-Venus d. WC Zverev-Zverev 7-5 7-6 (4) 1-Feb Ecuador Open Quito (C) Quito $463520 5 Victor Estrella Burgos d. 2 Thomaz Bellucci 4-6 7-6 (5) 6-2 Carreño Busta-Duran d. -

Twilight Doubles Pennant Winners VETSET Is the Newsletter of Tennis Sen- Iors ACT Incorporated
TENNIS SENIORS ACT INC WINTER ISSUE JUNE 2016 PREFACE Twilight Doubles Pennant Winners VETSET is the newsletter of Tennis Sen- iors ACT Incorporated. However the views expressed in the newsletter are not necessarily those of the committee. Membership fees for 2016/17 are due on 1 July - only $20. A membership form can be found on page 12 or on the web- site. The 2015/16 Committee comprises: President Pat Moloney (6262 3727) Vice President Graham Smith (6161 5352) Secretary Gail Jones (6254 4240) Treasurer Peter Breugelmans (6258 4261) Asst Secretary Kerry Scarlett (6291 5233) Committee John Greenup (6254 5263) The winners - Kerry Scarlett, Graeme Ainsworth, Leonie Ainsworth, Cameron Colin Lyons (0434 531 449) Steele with Vice President Graham Smith and their winnings. Full story page 8. Barbara McCluskey (6241 4402) Warren Muller (6231 0825) Annual General Meeting Website: www.tennisseniors.org.au/act The Tennis Seniors AGM will be held on Wednesday 7 September at 6.00pm, venue to be advised. Mark this date in your diary. Inside Page President’s Report 2 Vacancy for President and Secretary Charity Day 2 Alzheimer’s Australia ACT 2 Pat Moloney and Gail Jones are not standing for re-election as President and Secre- Adelaide 2017 (SA17) 3 tary at the AGM. They consider they have been there long enough and it is time 2016 World Young Seniors 3 for someone else to take over the positions and bring in some new thoughts and Tributes 4,5 ideas into the Committee. Further information can be obtained from Gail. Pat is Visitors from NZ 5 currently away on holidays and returning mid-August. -

ADCTF Annual Report 2013
THE AUSTRALIAN DAVIS CUP 2013 TENNIS FOUNDATION ANNUAL Approved by Tennis Australia REPORT THE AUSTRALIAN DAVIS CUP TENNIS FOUNDATION annual report 2013 1 THE AUSTRALIAN DAVIS CUP TENNIS FOUNDATION annual report 2013 2 THE AUSTRALIAN DAVIS CUP TENNIS FOUNDATION ABN 90 004 905 060 NOTICE OF ANNUAL GENERAL MEETING Notice is hereby given that the forty-second Annual General Meeting of The Australian Davis Cup Tennis Foundation will be held in the Clubhouse of the Royal South Yarra Lawn Tennis Club, Williams Road North, Toorak, on Thursday, 28th November 2013 at 8.00pm. BUSINESS 1. To receive, consider and if thought fit, to adopt the Directors' Report, the Directors' Declaration, the Statement of Financial Position as at 30th June 2013, the Statement of Comprehensive Income, the Statement of Cash Flows and the Statement of Changes in Equity for the year ended 30th June 2013 together with the Auditor's Report thereon. 2. To elect A President Two Vice-Presidents An Honorary Secretary An Honorary Treasurer and not less than three or more than seven other Directors. 3. Special Business To consider, and if though fit, to pass the following resolution as a special resolution:- “That the Foundation adopt the Constitution made available to members on the Foundations website, tabled and signed by the Chairman and marked ”A”, for the purposes of identification in place of its existing constitution.” 4. To transact any other business that, being lawfully brought forward, is accepted by the Chairman for discussion. BY ORDER OF THE BOARD Graeme K Cumbrae-Stewart OAM Honorary Secretary. Melbourne, 7th October, 2013 PROXIES A Member entitled to attend and vote at the Meeting is entitled to appoint one proxy to attend and vote in his or her stead. -

2020 Media Guide
2020 Media Guide Feb. 14-16 Feb. 15-23 YellowTennisBall.com 2020 QUICK FACTS EXECUTIVE STAFF ATP TOUR 250 EVENT DATES Tournament Director.................Mark Baron Main Draw .......................................Feb. 17-23 February 14-23, 2020 Tournament Chairman .............. Ivan Baron 16-Player Qualifying: ..................Feb. 15-16 Executive Director ......................John Butler Main Draw ....32 singles, 16-team doubles EVENT HISTORY Dir. Business Development, Sponsor Singles Format .......Best of 3 tie-break sets ATP 250: 28th Annual Liaison & Ticketing ...................Adam Baron Doubles Format ...............2 sets to 6 games ATP Champions Tour: 12th Annual Dir. Social Media, Volunteers, VolleyGirls, (no-ad scoring) with regular tie-break 6-6 22nd Year in Delray Beach Sponsor Relations ................... Marlena Hall Match tie-break at one-set each Assistant Special Events and Ticketing (1st team to 10 pts, win by 2) TITLE SPONSOR Manager ...............................Alexis Crenshaw Total Prize Money ........................... $673,655 City of Delray Beach Singles Winner ....................................$97,585 PRESENTING SPONSOR SUPPORT STAFF Doubles Winners................................$34,100 VITACOST.com Ball Kids Coordinator ................Monica Sica 2019 Singles Champion ........... Radu Albot Media Dir ........Natalie Milkolich-Cintorino 2019 Doubles Champions .............................. TOURNAMENT DIRECTOR Public Relations ...................................BlueIvy Bob & Mike Bryan Mark S. Baron -

2018-19 Baylor Men's Tennis Media Almanac
2018-19 BAYLOR MEN’S TENNIS MEDIA ALMANAC 10th Edition, Baylor Athletics Communications BAYLOR UNIVERSITY DEPARTMENT OF ATHLETICS 1500 South University Parks Drive Waco, TX 76706 254-710-1234 www.BaylorBears.com Facebook: BaylorAthletics Twitter: @BaylorAthletics CREDITS EDITORS Cody Soto, Kyle Robarts COMPILATION Cody Soto PHOTOGRAPHY Robbie Rogers, Matthew Minard Baylor Photography © 2019, Baylor University Department of Athletics BAYLOR UNIVERSITY MISSION STATEMENT The mission of Baylor University is to educate men and women for worldwide leadership and service by integrating academic excellence and Christian commitment within a caring community. BAYLOR ATHLETICS MISSION STATEMENT To support the overall mission of the University by providing a nationally competitive intercollegiate athletics program that attracts, nurtures and graduates student-athletes who, under the guidance of a high-quality staff, pursue excellence in their respective sports, while representing Baylor with character and integrity. Consistent with the Christian values of the University, the department will carry out this mission in a way that reflects fair and equitable opportunities for all student-athletes and staff. Baylor University is an equal opportunity institution whose programs, services, activities and operations are without discrimina- tion as to sex, color, or national origin, and are not opposed to qualified handicapped persons. 2018-19 BAYLOR MEN’S TENNIS MEDIA ALMANAC @BAYLORMTENNIS TABLE OF CONTENTS INTRODUCTION QUICK FACTS INTRODUCTION INTRODUCTION HISTORY Quick Facts/Media Information 1 All-Time Results 20-28 UNIVERSITY INFORMATION Athletics Communications 2 Yearly Records 29 Location: Waco, Texas Schedule 3 Series Records 30-34 Chartered: 1845, by the Republic of Texas University Administration 4 NCAA Tournament History/Apperances 35-48 Enrollment: 16,959 Director of Athletics 5 Letterwinners 49 President: Dr. -

Hotel- Trends Von Der Adria Bis Zum Gardasee Interviewstich Mit Dem Turnierdirektor Zu Seinem Diesjährigen Jubiläum
DEUTSCHLAND 7,– EURO | ÖSTERREICH 8,– EURO TENNIS, REISEN UND LIFESTYLE DOMINIC THIEM ZURÜCK AM ROTHENBAUM Der Österreicher will das Turnier unbedingt gewinnen AUS TRADITION INNOVATIV Der Technologiekonzern Panasonic feiert seinen 100. Geburtstag PURES SYLT-FEELING Es lebe der Strandkorb MICHAEL HOTEL- TRENDS VON DER ADRIA BIS ZUM GARDASEE INTERVIEWSTICH MIT DEM TURNIERDIREKTOR ZU SEINEM DIESJÄHRIGEN JUBILÄUM OFFIZIELLES MAGAZIN DER GERMAN OPEN AM ROTHENBAUM GAME CHANGING DELIVERY. Wollen Sie wissen, warum die Top-Spieler der Welt so erfolgreich sind? In der FedEx ATP Performance Zone auf atpworldtour.com können Sie Ergebnisse analysieren, Rekorde vergleichen und entdecken, was Erfolg wirklich ausmacht. fedex.com/atp4 rothenbaum Magazin GRUSSWORT beginnen möchte ich mit dem Wichtigsten: Ich möchte mich bei sönlich sehr traurig, Euch allen für zehn Jahre Treue, Respekt, Leidenschaft und fan- dass nun meine tastische Unterstützung bedanken. In der ganzen Zeit wart Ihr fast 40-jährige einzigartig und seid es immer noch. Verbindung mit diesem Tur- Vor zehn Jahren sind wir angetreten, um ein am Boden liegendes nier zu Ende Turnier zu retten. Ein Event, das vom DTB Anfang der 2000er geht. Und es Jahre über viele Jahre hinweg falsch und schlecht ausgerichtet und ist menschlich vermarktet wurde. Ich habe immer an die Idee geglaubt, an die sehr enttäu- GAME Geschichte und an die Unterstützung der vielen Menschen in die- schend, dass mir ser Stadt, die das Turnier und seine Tradition lieben und sich ihm die derzeit Verant- verbunden fühlen. Am Anfang war es harte Arbeit. Aber mit dem wortlichen auf Sei- damaligen DTB-Präsidenten Herrn von Waldenfels und dem Ge- ten des DTB nie eine CHANGING schäftsführer Herrn Kroeker hatten wir beim Verband handelnde Wertschätzung für das MIC H Personen, die an uns und unsere Vision glaubten. -

Teenage Tennis Players with the Best Chance to Become Grand Slam Champions
Teenage Tennis Players with the Best Chance to Become Grand Slam Champions Could American Taylor Fritz be another Juan Martin del Potro? Is Borna Coric the next Novak Djokovic? Will Switzerland's Belinda Bencic one day hoist as many major trophies as her compatriot Martina Hingis? Could Naomi Osaka surpass Kei Nishikori as Japan's best hope of winning a Grand Slam? Simply being one of the highest-ranked teens on the ATP World Tour or WTA Tour doesn't automatically qualify a player as a future Slam winner. American Catherine Bellis is having her best year and is ranked No. 115. However, she doesn't make the list because she lacks the size and serve of what has become the prototypical Slam winner in the women's game. So, who are the quick studies? The following are teenagers with the best chance of becoming Grand Slam champions. Jelena Ostapenko, Francis Tiafoe and Jared Donaldson get honorable mentions. Latvia's Ostapenko, 19, is ranked No. 46. This year she reached the final in Doha, Qatar, and has wins over Caroline Wozniacki, Petra Kvitova and Svetlana Kuznetsova. Nina Pantic of Tennis.com wrote, "The 5'10" Ostapenko has an aggressive baseliner’s style of play, combined with just enough patience to wait for the right opportunity." Tiafoe, 18, is among a handful of players hoping to end the Grand Slam drought for American men. After surviving a five-set match against Tiafoe at the U.S. Open, John Isner told reporters the teen's "backhand is world-class," per ESPN's Greg Garber. -
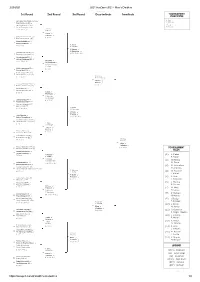
2/20/2021 2021 Ausopen 2021 - Men's Doubles
2/20/2021 2021 AusOpen 2021 - Men's Doubles COVIDSafe Information 1st Round 2nd Round 3rd Round Quarterfinals Semifinals TOURNAMENT CHAMPION R. Ram Juan Sebastian Cabal (COL) (1) 1 J. Salisbury Robert Farah (COL) (1) Nikoloz Basilashvili (GEO) I. Dodig 2 Andre Begemann (GER) F. Polasek J. Cabal 65-77 78-66 6-4 R. Farah A. Bublik A. Golubev Salvatore Caruso (ITA) (A) 6-4 6-4 3 Emil Ruusuvuori (FIN) (A) Alexander Bublik (KAZ) 4 Andrey Golubev (KAZ) A. Bublik 78-66 7-5 A. Golubev M. Arevalo M. Middelkoop Marcelo Demoliner (BRA) 64-77 77-63 6-3 5 Santiago Gonzalez (MEX) Marcelo Arevalo (ESA) 6 Matwe Middelkoop (NED) 61-77 78-66 6-3 M. Arevalo M. Middelkoop M. Kecmanovic C. Ruud (SRB) Miomir Kecmanovic 6-3 6-1 7 Casper Ruud (NOR) Robin Haase (NED) (13) 8 Oliver Marach (AUT) (13) M. Arevalo 6-3 1-6 6-0 M. Middelkoop J. Murray B. Soares Jeremy Chardy (FRA) (12) 6-3 6-4 9 Fabrice Martin (FRA) (12) Simone Bolelli (ITA) 10 Maximo Gonzalez (ARG) 6-3 6-4 S. Bolelli M. Gonzalez L. Sonego A. Vavassori (ITA) Lorenzo Sonego 6-2 77-65 11 Andrea Vavassori (ITA) Romain Arneodo (MON) 12 Benoit Paire (FRA) S. Bolelli 67-79 6-2 6-4 M. Gonzalez J. Murray B. Soares Laslo Djere (SRB) 13 65-77 6-2 6-4 Stefano Travaglia (ITA) Andrew Harris (AUS) (WC) 14 Alexei Popyrin (AUS) (WC) L. Djere 6-3 6-4 S. Travaglia J. Murray B. Soares Marcos Giron (USA) 6-1 6-2 15 Cameron Norrie (GBR) Jamie Murray (GBR) (6) 16 Bruno Soares (BRA) (6) J. -

Seven's Summer of Tennis Set to Sizzle
Seven’s Summer of Tennis set to sizzle LIVE and FREE streaming all summer via a brand new Mobile App experience 7Tennis, including 16 TV courts at Australian Open (10 December 2015) Seven will serve up all the big stars of the tennis world, including Federer, Djokovic, Nadal, Williams, Stosur, Kyrgios and Tomic, on all platforms again allowing viewers to watch live and free anywhere, anytime, on any device. From the Hopman Cup in Perth and the Brisbane International, to Sydney’s APIA International and the Kooyong Classic in Melbourne, all roads on Seven this summer lead to the first Grand Slam of 2016, the Australian Open. In addition to live and exclusive match coverage on Channel 7 and 7TWO, fans will be able to watch every tournament during the Summer of Tennis streamed live on mobile, tablet and PC via 7Tennis. This exclusive live and free online coverage through a brand new 7Tennis app will also allow fans to watch the match of their choice from any TV court throughout the summer – as well as the 7 / 7TWO/7mate broadcast. Fans will also get to choose from up to 16 TV courts at the Australian Open at any one time. And more than just live streaming, viewers will be able to catch up on match highlights, follow players on social media, interact with other fans and keep an eye on live scores. So whether it’s on free-to-air TV, or 7Tennis, Seven will deliver the most comprehensive and compelling coverage of the Australian tennis summer ever seen. -

DELRAY BEACH ATP 250 SINGLES SEEDS (Thru 2020)
(DELRAY BEACH ATP 250 SINGLES SEEDS (thru 2020 2020 1. Nick Kyrgios WD (Withdrew before tournament) 2. Milos Raonic SF 3. Taylor Fritz 1R 4. Reilly Opelka W 5. John Millman 1R 6. Ugo Humbert SF 7. Adrian Mannarino 1R 8. Radu Albot 1R 2019 1. Juan Martin del Potro QF (Lost to Mackenzie McDonald) 2. John Isner SF 3. Frances Tiafoe 1R 4. Steve Johnson QF 5. John Millman 1R 6. Andreas Seppi QF 7. Taylor Fritz 1R 8. Adrian Mannarino QF 2018 1. Jack Sock 2R (Lost to Reilly Opelka) 2. Juan Martin del Potro 2R 3. Kevin Anderson WD 4. Sam Querrey 1R 5. Nick Kyrgios WD 6. John Isner 2R 7. Adrian Mannarino WD 8. Hyeon Chung QF 9. Milos Raonic 2R 2017 1. Milos Raonic F (Lost to Jack Sock) 2. Ivo Karlovic 1R 3. Jack Sock W 4. Sam Querrey QF 5. Steve Johnson QF 6. Bernard Tomic 1R 7. Juan Martin del Potro SF 8. Kyle Edmund QF 2016 1. Kevin Anderson 1R (Lost to Austin Krajicek) 2. Bernard Tomic 1R 3. Ivo Karlovic 1R 4. Grigor Dimitrov SF 5. Jeremy Chardy QF 6. Steve Johnson 2R 7. Donald Young 2R 8. Adrian Mannarino QF 2015 (Kevin Anderson 2R (Lost to Yen-Hsun Lu .1 2. John Isner 1R 3. Alexandr Dolgopolov QF 4. Ivo Karlovic W 5. Adrian Mannarino SF 6. Sam Querrey 1R 7. Steve Johnson QF 8. Viktor Troicki 2R 2014 1. Tommy Haas 2R (Lost to Q Steve Johnson) 2. John Isner SF 3. Kei Nishikori 2R 4. Kevin Anderson F 5.