Astronomy Through the Ages 1 Early History and Greek Astronomy
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mathematicians
MATHEMATICIANS [MATHEMATICIANS] Authors: Oliver Knill: 2000 Literature: Started from a list of names with birthdates grabbed from mactutor in 2000. Abbe [Abbe] Abbe Ernst (1840-1909) Abel [Abel] Abel Niels Henrik (1802-1829) Norwegian mathematician. Significant contributions to algebra and anal- ysis, in particular the study of groups and series. Famous for proving the insolubility of the quintic equation at the age of 19. AbrahamMax [AbrahamMax] Abraham Max (1875-1922) Ackermann [Ackermann] Ackermann Wilhelm (1896-1962) AdamsFrank [AdamsFrank] Adams J Frank (1930-1989) Adams [Adams] Adams John Couch (1819-1892) Adelard [Adelard] Adelard of Bath (1075-1160) Adler [Adler] Adler August (1863-1923) Adrain [Adrain] Adrain Robert (1775-1843) Aepinus [Aepinus] Aepinus Franz (1724-1802) Agnesi [Agnesi] Agnesi Maria (1718-1799) Ahlfors [Ahlfors] Ahlfors Lars (1907-1996) Finnish mathematician working in complex analysis, was also professor at Harvard from 1946, retiring in 1977. Ahlfors won both the Fields medal in 1936 and the Wolf prize in 1981. Ahmes [Ahmes] Ahmes (1680BC-1620BC) Aida [Aida] Aida Yasuaki (1747-1817) Aiken [Aiken] Aiken Howard (1900-1973) Airy [Airy] Airy George (1801-1892) Aitken [Aitken] Aitken Alec (1895-1967) Ajima [Ajima] Ajima Naonobu (1732-1798) Akhiezer [Akhiezer] Akhiezer Naum Ilich (1901-1980) Albanese [Albanese] Albanese Giacomo (1890-1948) Albert [Albert] Albert of Saxony (1316-1390) AlbertAbraham [AlbertAbraham] Albert A Adrian (1905-1972) Alberti [Alberti] Alberti Leone (1404-1472) Albertus [Albertus] Albertus Magnus -

Implementing Eratosthenes' Discovery in the Classroom: Educational
Implementing Eratosthenes’ Discovery in the Classroom: Educational Difficulties Needing Attention Nicolas Decamp, C. de Hosson To cite this version: Nicolas Decamp, C. de Hosson. Implementing Eratosthenes’ Discovery in the Classroom: Educational Difficulties Needing Attention. Science and Education, Springer Verlag, 2012, 21 (6), pp.911-920. 10.1007/s11191-010-9286-3. hal-01663445 HAL Id: hal-01663445 https://hal.archives-ouvertes.fr/hal-01663445 Submitted on 18 Dec 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Sci & Educ DOI 10.1007/s11191-010-9286-3 Implementing Eratosthenes’ Discovery in the Classroom: Educational Difficulties Needing Attention Nicolas De´camp • Ce´cile de Hosson Ó Springer Science+Business Media B.V. 2010 Abstract This paper presents a critical analysis of the accepted educational use of the method performed by Eratosthenes to measure the circumference of Earth which is often considered as a relevant means of dealing with issues related to the nature of science and its history. This method relies on a number of assumptions among which the parallelism of sun rays. The assumption of sun rays parallelism (if it is accurate) does not appear spontaneous for students who consider sun rays to be divergent. -

Astronomy and Hipparchus
CHAPTER 9 Progress in the Sciences: Astronomy and Hipparchus Klaus Geus Introduction Geography in modern times is a term which covers several sub-disciplines like ecology, human geography, economic history, volcanology etc., which all con- cern themselves with “space” or “environment”. In ancient times, the definition of geography was much more limited. Geography aimed at the production of a map of the oikoumene, a geographer was basically a cartographer. The famous scientist Ptolemy defined geography in the first sentence of his Geographical handbook (Geog. 1.1.1) as “imitation through drafting of the entire known part of the earth, including the things which are, generally speaking, connected with it”. In contrast to chorography, geography uses purely “lines and label in order to show the positions of places and general configurations” (Geog. 1.1.5). Therefore, according to Ptolemy, a geographer needs a μέθοδος μαθεματική, abil- ity and competence in mathematical sciences, most prominently astronomy, in order to fulfil his task of drafting a map of the oikoumene. Given this close connection between geography and astronomy, it is not by default that nearly all ancient “geographers” (in the limited sense of the term) stood out also as astronomers and mathematicians: Among them Anaximander, Eudoxus, Eratosthenes, Hipparchus, Poseidonius and Ptolemy are the most illustrious. Apart from certain topics like latitudes, meridians, polar circles etc., ancient geography also took over from astronomy some methods like the determina- tion of the size of the earth or of celestial and terrestrial distances.1 The men- tioned geographers Anaximander, Eudoxus, Hipparchus, Poseidonius and Ptolemy even constructed instruments for measuring, observing and calculat- ing like the gnomon, sundials, skaphe, astrolabe or the meteoroscope.2 1 E.g., Ptolemy (Geog. -

Models for Earth and Maps
Earth Models and Maps James R. Clynch, Naval Postgraduate School, 2002 I. Earth Models Maps are just a model of the world, or a small part of it. This is true if the model is a globe of the entire world, a paper chart of a harbor or a digital database of streets in San Francisco. A model of the earth is needed to convert measurements made on the curved earth to maps or databases. Each model has advantages and disadvantages. Each is usually in error at some level of accuracy. Some of these error are due to the nature of the model, not the measurements used to make the model. Three are three common models of the earth, the spherical (or globe) model, the ellipsoidal model, and the real earth model. The spherical model is the form encountered in elementary discussions. It is quite good for some approximations. The world is approximately a sphere. The sphere is the shape that minimizes the potential energy of the gravitational attraction of all the little mass elements for each other. The direction of gravity is toward the center of the earth. This is how we define down. It is the direction that a string takes when a weight is at one end - that is a plumb bob. A spirit level will define the horizontal which is perpendicular to up-down. The ellipsoidal model is a better representation of the earth because the earth rotates. This generates other forces on the mass elements and distorts the shape. The minimum energy form is now an ellipse rotated about the polar axis. -

Anaximander and the Problem of the Earth's Immobility
Binghamton University The Open Repository @ Binghamton (The ORB) The Society for Ancient Greek Philosophy Newsletter 12-28-1953 Anaximander and the Problem of the Earth's Immobility John Robinson Windham College Follow this and additional works at: https://orb.binghamton.edu/sagp Recommended Citation Robinson, John, "Anaximander and the Problem of the Earth's Immobility" (1953). The Society for Ancient Greek Philosophy Newsletter. 263. https://orb.binghamton.edu/sagp/263 This Article is brought to you for free and open access by The Open Repository @ Binghamton (The ORB). It has been accepted for inclusion in The Society for Ancient Greek Philosophy Newsletter by an authorized administrator of The Open Repository @ Binghamton (The ORB). For more information, please contact [email protected]. JOHN ROBINSON Windham College Anaximander and the Problem of the Earth’s Immobility* N the course of his review of the reasons given by his predecessors for the earth’s immobility, Aristotle states that “some” attribute it I neither to the action of the whirl nor to the air beneath’s hindering its falling : These are the causes with which most thinkers busy themselves. But there are some who say, like Anaximander among the ancients, that it stays where it is because of its “indifference” (όμοιότητα). For what is stationed at the center, and is equably related to the extremes, has no reason to go one way rather than another—either up or down or sideways. And since it is impossible for it to move simultaneously in opposite directions, it necessarily stays where it is.1 The ascription of this curious view to Anaximander appears to have occasioned little uneasiness among modern commentators. -

1.1 Eratosthenes Measures the Earth (Copyright: Bryan Dorner All Rights Reserved)
1.1 Eratosthenes Measures the Earth (Copyright: Bryan Dorner all rights reserved) How big is the Earth? The mathematician Eratosthenes (276-195 BCE) lived in the city of Alexandria in northern Egypt near the place where the Nile river empties into the Mediterranean. Eratosthenes was chief librarian at the Alexandria museum and one of the foremost scholars of the day - second only to Archimedes (who many consider one of the two or three best mathematicians ever to have lived). The city of Alexandria had been founded about one hundred years earlier by Alexander the Great whose conquests stretched from Egypt, through Syria, Babylonia, and Persia to northern India and central Asia. As the Greeks were also called Hellenes, the resulting empire was known as the Hellenistic empire and the following period in which Greek culture was dominant is called the Hellenistic age. The Hellenistic age saw a considerable exchange of culture between the conquering Greeks and the civilizations of the lands they controlled. It is from about this period that the predominantly geometric mathematics of the Greeks shows a computational aspect borrowed from the Babylonians. Some of the best mathematics we have inherited comes from just such a blend of contributions from diverse cultures. Eratosthenes is known for his simple but accurate measurement of the size of the earth. The imprint of Babylon (modern Iraq) as well as Greece can be seen in his method. He did not divide the arc of a circle into 360 parts as the Babylonians did, but into 60 equal parts. Still, the use of 60 reveals the influence of the Babylonian number system - the sexagesimal system - which was based on the number 60 in the same way ours is based on the number 10. -

Meet the Philosophers of Ancient Greece
Meet the Philosophers of Ancient Greece Everything You Always Wanted to Know About Ancient Greek Philosophy but didn’t Know Who to Ask Edited by Patricia F. O’Grady MEET THE PHILOSOPHERS OF ANCIENT GREECE Dedicated to the memory of Panagiotis, a humble man, who found pleasure when reading about the philosophers of Ancient Greece Meet the Philosophers of Ancient Greece Everything you always wanted to know about Ancient Greek philosophy but didn’t know who to ask Edited by PATRICIA F. O’GRADY Flinders University of South Australia © Patricia F. O’Grady 2005 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise without the prior permission of the publisher. Patricia F. O’Grady has asserted her right under the Copyright, Designs and Patents Act, 1988, to be identi.ed as the editor of this work. Published by Ashgate Publishing Limited Ashgate Publishing Company Wey Court East Suite 420 Union Road 101 Cherry Street Farnham Burlington Surrey, GU9 7PT VT 05401-4405 England USA Ashgate website: http://www.ashgate.com British Library Cataloguing in Publication Data Meet the philosophers of ancient Greece: everything you always wanted to know about ancient Greek philosophy but didn’t know who to ask 1. Philosophy, Ancient 2. Philosophers – Greece 3. Greece – Intellectual life – To 146 B.C. I. O’Grady, Patricia F. 180 Library of Congress Cataloging-in-Publication Data Meet the philosophers of ancient Greece: everything you always wanted to know about ancient Greek philosophy but didn’t know who to ask / Patricia F. -

Eudoxus Erin Sondgeroth 9/1/14
Eudoxus Erin Sondgeroth 9/1/14 There were many brilliant mathematicians from the time period of 500 BC until 300 BC, including Pythagoras and Euclid. Another fundamental figure from that era was Greek mathematician Eudoxus of Cnidus. Eudoxus was born in Cnidus (present-day Turkey) in approximately 408 BC and died in 355 BC at the age of 53. Eudoxus studied math under Archytus in Tarentum, medicine under Philistium in Sicily, astronomy in Egytpt, and philosophy and rhetoric under Plato in Athens. After his many years of studying, Eudoxus established his own school at Cyzicus, where had many pupils. In 365 BC Eudoxus moved his school to Athens in order to work as a colleague of Plato. It was during this time that Eudoxus completed some of his best work and the reasoning for why he is considered the leading mathematician and astronomer of his day. In the field of astronomy, Eudoxus`s best-known work was his planetary model. This model had a spherical Earth that was at rest in the center of the universe and twenty-seven concentric spheres that held the fixed stars, sun, moon, and other planets that moved in orbit around the Earth. While this model has clearly been disproved, it was a prominent model for at least fifty years because it explained many astronomical phenomenon of that time, including the sunrise and sunset, the fixed constellations, and movement of other planets in orbits. Luckily, Eudoxus`s theories had much more success in the field of mathemat- ics. Many of his proposition, theories, and proofs are common knowledge in the math world today. -

9 · the Growth of an Empirical Cartography in Hellenistic Greece
9 · The Growth of an Empirical Cartography in Hellenistic Greece PREPARED BY THE EDITORS FROM MATERIALS SUPPLIED BY GERMAINE AUJAe There is no complete break between the development of That such a change should occur is due both to po cartography in classical and in Hellenistic Greece. In litical and military factors and to cultural developments contrast to many periods in the ancient and medieval within Greek society as a whole. With respect to the world, we are able to reconstruct throughout the Greek latter, we can see how Greek cartography started to be period-and indeed into the Roman-a continuum in influenced by a new infrastructure for learning that had cartographic thought and practice. Certainly the a profound effect on the growth of formalized know achievements of the third century B.C. in Alexandria had ledge in general. Of particular importance for the history been prepared for and made possible by the scientific of the map was the growth of Alexandria as a major progress of the fourth century. Eudoxus, as we have seen, center of learning, far surpassing in this respect the had already formulated the geocentric hypothesis in Macedonian court at Pella. It was at Alexandria that mathematical models; and he had also translated his Euclid's famous school of geometry flourished in the concepts into celestial globes that may be regarded as reign of Ptolemy II Philadelphus (285-246 B.C.). And it anticipating the sphairopoiia. 1 By the beginning of the was at Alexandria that this Ptolemy, son of Ptolemy I Hellenistic period there had been developed not only the Soter, a companion of Alexander, had founded the li various celestial globes, but also systems of concentric brary, soon to become famous throughout the Mediter spheres, together with maps of the inhabited world that ranean world. -

10 · Greek Cartography in the Early Roman World
10 · Greek Cartography in the Early Roman World PREPARED BY THE EDITORS FROM MATERIALS SUPPLIED BY GERMAINE AUJAe The Roman republic offers a good case for continuing to treat the Greek contribution to mapping as a separate CONTINUITY AND CHANGE IN THEORETICAL strand in the history ofclassical cartography. While there CARTOGRAPHY: POLYBIUS, CRATES, was a considerable blending-and interdependence-of AND HIPPARCHUS Greek and Roman concepts and skills, the fundamental distinction between the often theoretical nature of the Greek contribution and the increasingly practical uses The extent to which a new generation of scholars in the for maps devised by the Romans forms a familiar but second century B.C. was familiar with the texts, maps, satisfactory division for their respective cartographic in and globes of the Hellenistic period is a clear pointer to fluences. Certainly the political expansion of Rome, an uninterrupted continuity of cartographic knowledge. whose domination was rapidly extending over the Med Such knowledge, relating to both terrestrial and celestial iterranean, did not lead to an eclipse of Greek influence. mapping, had been transmitted through a succession of It is true that after the death of Ptolemy III Euergetes in well-defined master-pupil relationships, and the pres 221 B.C. a decline in the cultural supremacy of Alex ervation of texts and three-dimensional models had been andria set in. Intellectual life moved to more energetic aided by the growth of libraries. Yet this evidence should centers such as Pergamum, Rhodes, and above all Rome, not be interpreted to suggest that the Greek contribution but this promoted the diffusion and development of to cartography in the early Roman world was merely a Greek knowledge about maps rather than its extinction. -

``Mathematics'' and ``Physics'' in the Science of Harmonics
NISSUNA UMANA INVESTIGAZIONE SI PUO DIMANDARE VERA SCIENZIA S’ESSA NON PASSA PER LE MATEMATICHE DIMOSTRAZIONI LEONARDO DA VINCI vol. 4 no. 3-4 2016 Mathematics and Mechanics of Complex Systems STEFANO ISOLA “MATHEMATICS” AND “PHYSICS” IN THE SCIENCE OF HARMONICS msp MATHEMATICS AND MECHANICS OF COMPLEX SYSTEMS Vol. 4, No. 3-4, 2016 dx.doi.org/10.2140/memocs.2016.4.213 ∩ MM “MATHEMATICS” AND “PHYSICS” IN THE SCIENCE OF HARMONICS STEFANO ISOLA Some aspects of the role that the science of harmonics has played in the history of science are discussed in light of Russo’s investigation of the history of the concepts of “mathematics” and “physics”. 1. The rambling route of the ancient scientific method In several places in Russo’s writings on the history of science, one can find en- lightening discussions about the meanings of the concepts of “physics” and “math- ematics”, along with the particular notions of truth involved in them; see, e.g., [58, Chapter 6.6; 60, Chapter 15; 56; 57]. Both terms derive from the Greek: the original meaning of the former was the investigation of everything that lives, grows or, more generally, comes into existence, whereas the latter referred to all that is studied, thus deriving its meaning not from its content but from its method. In the Hellenistic period, the term “physics” continued to be used to indicate that sector of philosophy that addressed nature (the other sectors being ethics and logic), thus corresponding to what came to be called “natural philosophy” in modern times. On the other hand, the term “mathematics” was used to indicate all the disciplines (including geometry, arithmetic, harmonics, astronomy, optics, mechanics, hydro- statics, pneumatics, geodesy and mathematical geography) that shared the same method of investigation, based on the construction of theories by which “theorems” are proved, leaning on explicitly stated initial assumptions. -
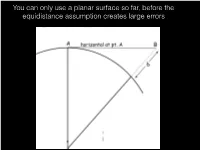
You Can Only Use a Planar Surface So Far, Before the Equidistance Assumption Creates Large Errors
You can only use a planar surface so far, before the equidistance assumption creates large errors Distance error from Kiester to Warroad is greater than two football fields in length So we assume a spherical Earth P. Wormer, wikimedia commons Longitudes are great circles, latitudes are small circles (except the Equator, which is a GC) Spherical Geometry Longitude Spherical Geometry Note: The Greek letter l (lambda) is almost always used to specify longitude while f, a, w and c, and other symbols are used to specify latitude Great and Small Circles Great circles splits the Small circles splits the earth into equal halves earth into unequal halves wikipedia geography.name All lines of equal longitude are great circles Equator is the only line of equal latitude that’s a great circle Surface distance measurements should all be along a great circle Caliper Corporation Note that great circle distances appear curved on projected or flat maps Smithsonian In GIS Fundamentals book, Chapter 2 Latitude - angle to a parallel circle, a small circle parallel to the Equatorial great circle Spherical Geometry Three measures: Latitude, Longitude, and Earth Radius + height above/ below the sphere (hp) How do we measure latitude/longitude? Well, now, GNSS, but originally, astronomic measurements: latitude by north star or solar noon angles, at equinox Longitude Measurement Method 1: The Earth rotates 360 degrees in a day, or 15 degrees per hour. If we know the time difference between 2 points, and the longitude of the first point (Greenwich), we can determine the longitude at our current location. Method 2: Create a table of moon-star distances for each day/time of the year at a reference location (Greenwich observatory) Measure the same moon-star distance somewhere else at a standard or known time.