DOCSLIB.ORG

Modelling the Liquid-Water Vein System Within Polar Ice Sheets As a Potential Microbial Habitat

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modelling the Liquid-Water Vein System Within Polar Ice Sheets As a Potential Microbial Habitat Earth and Planetary Science Letters 333–334 (2012) 238–249 Contents lists available at SciVerse ScienceDirect Earth and Planetary Science Letters journal homepage: www.elsevier.com/locate/epsl Modelling the liquid-water vein system within polar ice sheets as a potential microbial habitat K.G. Srikanta Dani a,1, Heidy M. Mader a,n, Eric W. Wolff b, Jemma L. Wadham c a School of Earth Sciences, University of Bristol, Wills Memorial Building, Queen’s Road, Bristol BS8 1RJ, UK b British Antarctic Survey, High Cross, Madingley Road, Cambridge CB3 0ET, UK c School of Geographical Sciences, University of Bristol, University Road, Bristol BS8 1SS, UK article info abstract Article history: Based on the fundamental and distinctive physical properties of polycrystalline ice Ih, the chemical and Received 12 October 2011 temperature profiles within the polar ice sheets, and the observed selective partitioning of bacteria into Received in revised form liquid water filled veins in the ice, we consider the possibility that microbial life could survive and be 21 March 2012 sustained within glacial systems. Here, we present a set of modelled vertical profiles of vein diameter, Accepted 6 April 2012 vein chemical concentration, and vein water volume variability across a range of polar ice sheets using Editor: G. Henderson Available online 22 May 2012 their ice core chemical profiles. A sensitivity analysis of VeinsInIce1.0, the numerical model used in this study shows that the ice grain size and the local borehole temperature are the most significant factors Keywords: that influence the intergranular liquid vein size and the amount of freeze-concentrated impurities polar ice cores partitioned into the veins respectively. Model results estimate the concentration and characteristics of polycrystalline ice the chemical broth in the veins to be a potential extremophilic microbial medium. The vein sizes are psychrophilic bacterial metabolism vein system estimated to vary between 0.3 mmto8mm across the vertical length of many polar ice sheets and they temperature depression may contain up to 2 mL of liquid water per litre of solid ice. The results suggest that these veins in polar ice sheets could accommodate populations of psychrophilic and hyperacidophilic ultra-small bacteria and in some regions even support the habitation of unicellular eukaryotes. This highlights the importance of understanding the potential impact of englacial microbial metabolism on polar ice core chemical profiles and provides a model for similar extreme habitats elsewhere in the universe. & 2012 Elsevier B.V. All rights reserved. 1. Introduction Fig. 1(a)–(e) shows the geometry of the intergranular vein system found in natural polycrystalline ice Ih (hexagonal ice) that The presence of bacteria and archaea in glaciers and ice sheets makes up the bulk of temperate glaciers and polar ice sheets on has been reported by numerous researchers (Abyzov, 1993; Karl Earth (Nye and Frank, 1973). The liquid water phase exists in solid et al., 1999; Siegert et al., 2001; Foght et al., 2004; Gaidos et al., ice because the ice lattice tends to reject foreign ions (impurities) 2004; Abyzov et al., 2005; Kastovska et al., 2007; Hodson et al., as water is frozen. In other words, the solubility of compounds in 2008). For many years it was thought that the extremely low the individual ice grains is generally very low and the expelled temperatures within natural ice deposits on Earth and the lack of foreign ions from the growing grains remain in the liquid water liquid water, light and nutrients in them presented too harsh an and become more concentrated with decreasing temperature. environment to sustain any form of life. More recently however it Ultimately, an ice polycrystal is formed which contains an inter- has been proposed that the intergranular aqueous vein system connected network of highly concentrated water-filled veins found in ice could provide a habitat capable of sustaining around ice grains and films on grain boundaries. microbial life (Price, 2000; Mader et al., 2006; Rohde and Price, Experiments have demonstrated that microorganisms partition 2007) on Earth and that similar habitats might exist on other icy preferentially to the veins during grain growth (Fig. 1(f)–(i), Mader heavenly bodies such as Mars and some icy moons of Jupiter and et al., 2006; Amato et al., 2009). Even at extreme sub-zero tempera- Saturn (Price, 2002, 2007; Parkinson et al., 2008; Newman et al., tures in the veins, bacteria can find both liquid water and much 2009). higher concentrations of nutrients (impurities) than the average impurity concentration estimated in bulk ice. Moreover, some psychrophilic microbes show active growth at temperatures as low n Corresponding author. Tel.: þ44 0117 9545445. as À12 1C(Breezee et al., 2004). Some are shown to be metabolically E-mail address: [email protected] (H.M. Mader). 1 Present address: Department of Biological Sciences, Macquarie University, active down to À20 1C(Gilichinsky, 2002; Price and Sowers, 2004) North Ryde, Sydney, NSW 2109, Australia. and À39 1C(Bakermans, 2008). However, the mechanisms that 0012-821X/$ - see front matter & 2012 Elsevier B.V. All rights reserved. http://dx.doi.org/10.1016/j.epsl.2012.04.009 K.G.S. Dani et al. / Earth and Planetary Science Letters 333–334 (2012) 238–249 239 Fig. 1. Ice vein geometry and partitioning of microbes into liquid veins in ice (for a detailed figure caption with explained notations, please see supplementary material 1. (a) SEM of a typical ice vein cross section at a triple junction (crystal edge). (b) Diagram of a vein cross-section. (c) Semi-regular truncated octahedron (represents an ice grain) and a sketch of vein network surrounding it (after Price, 2000). (d and e) Transmitted white lightphotographs of the vein system in laboratory-grown ice (from Mader, 1992a); veins are 100 mm across. It is a curious point to note that tetrahedral geometry of nodes complements the inherent structural tendency towards stability of water molecules that cluster to form hydrogen bonds in a tetrahedral geometry. (f) Light and (g) fluorescence micrographs showing 1.9 mm fluorescent beads (size equivalent of bacteria) lined up along an ice vein running into a node (from Mader et al., 2006). (h) Bright field and (i) 510–560 nm epifluorescent micrographs showing yeast cells (44 mm) within an ice vein triple junction of size 410 mm (reproduced with permission from Amato et al., 2009). The scale on (f) applies to all the 4 photographs. enable maintenance of microbial intracellular fluidity at subzero A sensitivity analysis of the numerical model (VeinsInIce1.0) temperatures remain uncertain (Russel, 2006). There are very limited allows us to draw inferences about the relative impact of the experimental and/or modelled data on the interaction of ice bio- parameters tested in the model on the features of the habitat. For chemistry and the microbial activities at extremely low temperatures ice veins to develop in polycrystalline ice, the deposited snow has (below À20 1C) within glacier ice (Rivkina et al., 2000; Junge et al., to be preserved and compressed over several hundred years, 2004; Bakermans, 2008). which is not observed in shallow perennial snowpacks (up to Inorganic impurities from polar ice cores have been studied in 50 m deep) and some temperate glaciers, which are mostly detail in the scientific literature because they can act as proxies characterised as either superficial fresh snow or firn ice. The for palaeoclimate reconstructions (e.g., Wolff et al., 2006, 2010). polar ice sheets are volumetrically the most significant on earth. It is known that temperature and chemical concentrations in For these reasons we consider only deep (100–3000 m) polar ice natural polycrystalline ice regulate the intergranular vein size sheets for our analysis to establish the conditions in the veins. (Mader, 1992b; Paterson, 1994) and hence control their water volume and potential microbial population carrying capacities. Furthermore the chemical concentrations control the diffusion rates of chemical impurities through grain boundaries and veins 2. Definitions and ultimately govern the microbial metabolic reactions, which in turn could impact on vein chemistry. Anomalies observed in polar In the following sections, it is important to distinguish care- ice core gas records (e.g. N2O, CH4) have been attributed to fully between various symbols and terms that are used to refer to potential in situ microbial activity (Sowers, 2001; Tung et al., impurity concentration. 2005). In addition, some models suggest that the rate of down- The bulk impurity concentration C is given by the total mass of ward diffusion of impurities along the liquid veins within ice impurity (usually given in moles) divided by the total ice volume sheets could be significantly more than the rate of rheological ice (grainsþveinsþgrain boundary films). In this paper the term bulk is flow in ice sheets and this can lead to a major displacement of always used for concentrations averaged across the total ice volume climate signals trapped in ice cores (Hubbard et al., 2003; Rempel in this way. The vein impurity concentration is cv and is simply the et al., 2001; Rempel and Wettlaufer, 2003). total mass of impurity that partitions to the veins divided by the We utilise selected site-specific data sets on temperature and total vein volume. It is assumed that this is also the impurity chemical impurity profiles of polar ice cores and combine these concentration in the grain boundary films. We can define an datasets with a numerical model (VeinsInIce1.0) that encapsulates associated bulk veinþfilm impurity concentration Cb which is the our knowledge of the physical properties of the vein system to total mass of impurity that partitions to the veins and films divided calculate vertical profiles of vein diameter, vein impurity con- by the total ice volume.
Load more

Recommended publications
  • Ice Ic” Werner F
    Extent and relevance of stacking disorder in “ice Ic” Werner F. Kuhsa,1, Christian Sippela,b, Andrzej Falentya, and Thomas C. Hansenb aGeoZentrumGöttingen Abteilung Kristallographie (GZG Abt. Kristallographie), Universität Göttingen, 37077 Göttingen, Germany; and bInstitut Laue-Langevin, 38000 Grenoble, France Edited by Russell J. Hemley, Carnegie Institution of Washington, Washington, DC, and approved November 15, 2012 (received for review June 16, 2012) “ ” “ ” A solid water phase commonly known as cubic ice or ice Ic is perfectly cubic ice Ic, as manifested in the diffraction pattern, in frequently encountered in various transitions between the solid, terms of stacking faults. Other authors took up the idea and liquid, and gaseous phases of the water substance. It may form, attempted to quantify the stacking disorder (7, 8). The most e.g., by water freezing or vapor deposition in the Earth’s atmo- general approach to stacking disorder so far has been proposed by sphere or in extraterrestrial environments, and plays a central role Hansen et al. (9, 10), who defined hexagonal (H) and cubic in various cryopreservation techniques; its formation is observed stacking (K) and considered interactions beyond next-nearest over a wide temperature range from about 120 K up to the melt- H-orK sequences. We shall discuss which interaction range ing point of ice. There was multiple and compelling evidence in the needs to be considered for a proper description of the various past that this phase is not truly cubic but composed of disordered forms of “ice Ic” encountered. cubic and hexagonal stacking sequences. The complexity of the König identified what he called cubic ice 70 y ago (11) by stacking disorder, however, appears to have been largely over- condensing water vapor to a cold support in the electron mi- looked in most of the literature.
    [Show full text]
  • A Primer on Ice
    A Primer on Ice L. Ridgway Scott University of Chicago Release 0.3 DO NOT DISTRIBUTE February 22, 2012 Contents 1 Introduction to ice 1 1.1 Lattices in R3 ....................................... 2 1.2 Crystals in R3 ....................................... 3 1.3 Comparingcrystals ............................... ..... 4 1.3.1 Quotientgraph ................................. 4 1.3.2 Radialdistributionfunction . ....... 5 1.3.3 Localgraphstructure. .... 6 2 Ice I structures 9 2.1 IceIh........................................... 9 2.2 IceIc........................................... 12 2.3 SecondviewoftheIccrystalstructure . .......... 14 2.4 AlternatingIh/Iclayeredstructures . ........... 16 3 Ice II structure 17 Draft: February 22, 2012, do not distribute i CONTENTS CONTENTS Draft: February 22, 2012, do not distribute ii Chapter 1 Introduction to ice Water forms many different crystal structures in its solid form. These provide insight into the potential structures of ice even in its liquid phase, and they can be used to calibrate pair potentials used for simulation of water [9, 14, 15]. In crowded biological environments, water may behave more like ice that bulk water. The different ice structures have different dielectric properties [16]. There are many crystal structures of ice that are topologically tetrahedral [1], that is, each water molecule makes four hydrogen bonds with other water molecules, even though the basic structure of water is trigonal [3]. Two of these crystal structures (Ih and Ic) are based on the same exact local tetrahedral structure, as shown in Figure 1.1. Thus a subtle understanding of structure is required to differentiate them. We refer to the tetrahedral structure depicted in Figure 1.1 as an exact tetrahedral structure. In this case, one water molecule is in the center of a square cube (of side length two), and it is hydrogen bonded to four water molecules at four corners of the cube.
    [Show full text]
  • Arxiv:2004.08465V2 [Cond-Mat.Stat-Mech] 11 May 2020
    Phase equilibrium of liquid water and hexagonal ice from enhanced sampling molecular dynamics simulations Pablo M. Piaggi1 and Roberto Car2 1)Department of Chemistry, Princeton University, Princeton, NJ 08544, USA a) 2)Department of Chemistry and Department of Physics, Princeton University, Princeton, NJ 08544, USA (Dated: 13 May 2020) We study the phase equilibrium between liquid water and ice Ih modeled by the TIP4P/Ice interatomic potential using enhanced sampling molecular dynamics simulations. Our approach is based on the calculation of ice Ih-liquid free energy differences from simulations that visit reversibly both phases. The reversible interconversion is achieved by introducing a static bias potential as a function of an order parameter. The order parameter was tailored to crystallize the hexagonal diamond structure of oxygen in ice Ih. We analyze the effect of the system size on the ice Ih-liquid free energy differences and we obtain a melting temperature of 270 K in the thermodynamic limit. This result is in agreement with estimates from thermodynamic integration (272 K) and coexistence simulations (270 K). Since the order parameter does not include information about the coordinates of the protons, the spontaneously formed solid configurations contain proton disorder as expected for ice Ih. I. INTRODUCTION ture forms in an orientation compatible with the simulation box9. The study of phase equilibria using computer simulations is of central importance to understand the behavior of a given model. However, finding the thermodynamic condition at II. CRYSTAL STRUCTURE OF ICE Ih which two or more phases coexist is particularly hard in the presence of first order phase transitions.
    [Show full text]
  • Modeling the Ice VI to VII Phase Transition
    Modeling the Ice VI to VII Phase Transition Dawn M. King 2009 NSF/REU PROJECT Physics Department University of Notre Dame Advisor: Dr. Kathie E. Newman July 31, 2009 Abstract Ice (solid water) is found in a number of different structures as a function of temperature and pressure. This project focuses on two forms: Ice VI (space group P 42=nmc) and Ice VII (space group Pn3m). An interesting feature of the structural phase transition from VI to VII is that both structures are \self clathrate," which means that each structure has two sublattices which interpenetrate each other but do not directly bond with each other. The goal is to understand the mechanism behind the phase transition; that is, is there a way these structures distort to become the other, or does the transition occur through the breaking of bonds followed by a migration of the water molecules to the new positions? In this project we model the transition first utilizing three dimensional visualization of each structure, then we mathematically develop a common coordinate system for the two structures. The last step will be to create a phenomenological Ising-like spin model of the system to capture the energetics of the transition. It is hoped the spin model can eventually be studied using either molecular dynamics or Monte Carlo simulations. 1 Overview of Ice The known existence of many solid states of water provides insight into the complexity of condensed matter in the universe. The familiarity of ice and the existence of many structures deem ice to be interesting in the development of techniques to understand phase transitions.
    [Show full text]
  • 11Th International Conference on the Physics and Chemistry of Ice, PCI
    11th International Conference on the Physics and Chemistry of Ice (PCI-2006) Bremerhaven, Germany, 23-28 July 2006 Abstracts _______________________________________________ Edited by Frank Wilhelms and Werner F. Kuhs Ber. Polarforsch. Meeresforsch. 549 (2007) ISSN 1618-3193 Frank Wilhelms, Alfred-Wegener-Institut für Polar- und Meeresforschung, Columbusstrasse, D-27568 Bremerhaven, Germany Werner F. Kuhs, Universität Göttingen, GZG, Abt. Kristallographie Goldschmidtstr. 1, D-37077 Göttingen, Germany Preface The 11th International Conference on the Physics and Chemistry of Ice (PCI- 2006) took place in Bremerhaven, Germany, 23-28 July 2006. It was jointly organized by the University of Göttingen and the Alfred-Wegener-Institute (AWI), the main German institution for polar research. The attendance was higher than ever with 157 scientists from 20 nations highlighting the ever increasing interest in the various frozen forms of water. As the preceding conferences PCI-2006 was organized under the auspices of an International Scientific Committee. This committee was led for many years by John W. Glen and is chaired since 2002 by Stephen H. Kirby. Professor John W. Glen was honoured during PCI-2006 for his seminal contributions to the field of ice physics and his four decades of dedicated leadership of the International Conferences on the Physics and Chemistry of Ice. The members of the International Scientific Committee preparing PCI-2006 were J.Paul Devlin, John W. Glen, Takeo Hondoh, Stephen H. Kirby, Werner F. Kuhs, Norikazu Maeno, Victor F. Petrenko, Patricia L.M. Plummer, and John S. Tse; the final program was the responsibility of Werner F. Kuhs. The oral presentations were given in the premises of the Deutsches Schiffahrtsmuseum (DSM) a few meters away from the Alfred-Wegener-Institute.
    [Show full text]
  • 2Growth, Structure and Properties of Sea
    Growth, Structure and Properties 2 of Sea Ice Chris Petrich and Hajo Eicken 2.1 Introduction The substantial reduction in summer Arctic sea ice extent observed in 2007 and 2008 and its potential ecological and geopolitical impacts generated a lot of attention by the media and the general public. The remote-sensing data documenting such recent changes in ice coverage are collected at coarse spatial scales (Chapter 6) and typically cannot resolve details fi ner than about 10 km in lateral extent. However, many of the processes that make sea ice such an important aspect of the polar oceans occur at much smaller scales, ranging from the submillimetre to the metre scale. An understanding of how large-scale behaviour of sea ice monitored by satellite relates to and depends on the processes driving ice growth and decay requires an understanding of the evolution of ice structure and properties at these fi ner scales, and is the subject of this chapter. As demonstrated by many chapters in this book, the macroscopic properties of sea ice are often of most interest in studies of the interaction between sea ice and its environment. They are defi ned as the continuum properties averaged over a specifi c volume (Representative Elementary Volume) or mass of sea ice. The macroscopic properties are determined by the microscopic structure of the ice, i.e. the distribution, size and morphology of ice crystals and inclusions. The challenge is to see both the forest, i.e. the role of sea ice in the environment, and the trees, i.e. the way in which the constituents of sea ice control key properties and processes.
    [Show full text]
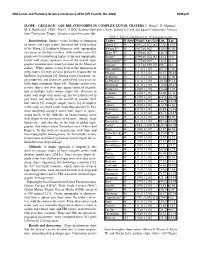
  • Slope - Geologic Age Relationships in Complex Lunar Craters C
    49th Lunar and Planetary Science Conference 2018 (LPI Contrib. No. 2083) 2399.pdf SLOPE - GEOLOGIC AGE RELATIONSHIPS IN COMPLEX LUNAR CRATERS C. Rojas1, P. Mahanti1, M. S. Robinson1, LROC Team1, 1LROC Science Operation Center, School of Earth and Space Exploration, Arizona State University, Tempe, Arizona ([email protected]) Table 1: List of complex craters. *Copernican craters Introduction: Impact events leading to formation Crater D (km) Model Age (Ga) Lon Lat of basins and large craters dominate the early history Moore F* 24 0.041∓0.012 [8] 37.30 185.0 of the Moon [1] leading to kilometer scale topographic Wiener F* 30 0.017∓0.002 149.9740.90 variations on the lunar surface, with smaller crater [2], Klute W* 31 0.090∓0.007 216.7037.98 progressively introducing higher frequency topography. Necho* 37 0.080∓0.024 [8] 123.3 –5.3 Crater wall slopes represent most of the overall topo- Aristarchus* 40 0.175∓0.0095 312.5 23.7 graphic variation since many locations on the Moon are Jackson* 71 0.147∓0.038 [9] 196.7 22.1 craters. While impact events lead to the formation of McLaughlin 75 3.7∓0.1 [10] 267.1747.01 steep slopes [3], they are also primarily responsible for Pitiscus 80 3.8∓0.1 [10] 30.57 -50.61 landform degradation [4]. During crater formation, tar- Al-Biruni 80 3.8∓0.1 [10] 92.62 18.09 get properties and processes controlling structural sta- La Pérouse 80 3.6∓0.1 [10] -10.66 76.18 bility limit maximum slopes [4].
    [Show full text]
  • Mechanical Characterization Via Full Atomistic Simulation: Applications to Nanocrystallized Ice
    Mechanical Characterization via Full Atomistic Simulation: Applications to Nanocrystallized Ice A thesis presented By Arvand M.H. Navabi to The Department of Civil and Environmental Engineering in partial fulfillment of the requirements for the degree of Master of Science in the field of Civil Engineering Northeastern University Boston, Massachusetts August, 2016 Submitted to Prof. Steven W. Cranford Acknowledgements I acknowledge generous support from my thesis advisor Dr. Steven W. Cranford whose encouragement and availability was crucial to this thesis and also my parents for allowing me to realize my own potential. The simulations were made possible by LAMMPS open source program. Visualization has been carried out using the VMD visualization package. 3 Abstract This work employs molecular dynamic (MD) approaches to characterize the mechanical properties of nanocrystalline materials via a full atomistic simulation using the ab initio derived ReaxFF potential. Herein, we demonstrate methods to efficiently simulate key mechanical properties (ultimate strength, stiffness, etc.) in a timely and computationally inexpensive manner. As an illustrative example, the work implements the described methodology to perform full atomistic simulation on ice as a material platform, which — due to its complex behavior and phase transitions upon pressure, heat exchange, energy transfer etc. — has long been avoided or it has been unsuccessful to ascertain its mechanical properties from a molecular perspective. This study will in detail explain full atomistic MD methods and the particulars required to correctly simulate crystalline material systems. Tools such as the ReaxFF potential and open-source software package LAMMPS will be described alongside their fundamental theories and suggested input methods to simulate further materials, encompassing both periodic and finite crystalline models.
    [Show full text]
  • Ice-Seven (Ice VII)
    Ice-seven (Ice VII) Ice-seven (ice VII) [1226] is formed from liquid water above 3 GPa by lowering its temperature to ambient temperatures (see Phase Diagram). It can be obtained at low temperature and ambient pressure by decompressing (D2O) ice-six below 95 K and is metastable over a wide range of pressure, transforming into LDA above 120 K [948]. Note that in this structural diagram the hydrogen bonding is ordered whereas in reality it is random (obeying the 'ice rules': two hydrogen atoms near each oxygen, one hydrogen atom on each O····O bond). As the H-O-H angle does not vary much from that of the isolated molecule, the hydrogen bonds are not straight (although shown so in the figures). The Ice VII unit cell, which forms cubic crystal ( , 224; Laue class symmetry m-3m) consists of two interpenetrating cubic ice lattices with hydrogen bonds passing through the center of the water hexamers and no connecting hydrogen-bonds between lattices. It has a density of about 1.65 g cm- 3 (at 2.5 GPa and 25 °C [8]), which is less than twice the cubic ice density as the intra-network O····O distances are 8% longer (at 0.1 MPa) to allow for the interpenetration. The cubic crystal (shown opposite) has cell dimensions 3.3501 Å (a, b, c, 90º, 90º, 90º; D2O, at 2.6 GPa and 22 °C [361]) and contains two water molecules. All molecules experience identical molecular environments. The hydrogen bonding is disordered and constantly changing as in hexagonal ice but ice-seven undergoes a proton disorder-order transition to ice-eight at about 5 °C; ice-seven and ice-eight having identical structures apart from the proton ordering.
    [Show full text]
  • © Cambridge University Press Cambridge
    Cambridge University Press 978-0-521-80620-6 - Creep and Fracture of Ice Erland M. Schulson and Paul Duval Index More information Index 100-year wave force, 336 friction and fracture, 289, 376 60° dislocations, 17, 82, 88 indentation failure, 345 microstructure, 45, 70, 237, 255, 273 abrasion, 337 multiscale fracture and frictional accommodation processes of basal slip, 165 sliding, 386 acoustic emission, 78, 90, 108 nested envelopes, 377 across-column cleavage cracks, 278 pressure–area relationship, 349, 352 across-column confinement, 282 S2 growth texture, 246, 273 across-column cracks, 282, 306, SHEBA faults, 371 across-column loading, 275 SHEBA stress states, 377 across-column strength, 246, 249, 275 Arctic Ocean, 1, 45, 190, 361 activation energy, 71, 84, 95, 111, 118, 131 aspect ratio, 344 activation volume, 114, 182 atmospheric ice, 219, 221, 241, 243 activity of pyramidal slip systems, 158 atmospheric icing, 31 activity of slip systems, 168 atmospheric impurities, 113 adiabatic heating, 291, 348 atomic packing factor, 9 adiabatic softening, 291 audible report, 240 affine self-consistent model, 160 avalanches, 206 air bubbles, 38 air-hydrate crystals, 37 bands, 89 albedo, 363 basal activity, 162 aligned first-year sea ice, 246 basal dislocations, 77 along-column confinement, 282 basal planes, 214, along-column confining stress, 282, basal screw dislocations, 77, 87 along-column strength, 244, 275 basal shear bands, 163 ammonia dihydrate, 181 basal slip, 18, 77, 127, 228 ammonia–water system, 186 basal slip lines, 77 amorphous forms
    [Show full text]
  • Hexagonal Ice (Ice Ih)
    Hexagonal Ice (Ice Ih) Some physical properties Ice nucleation and growth Is ice slippery? Hexagonal ice (ice Ih) [1969]. is the form of all natural snow and ice on Earth (see Phase Diagram), as evidenced in the six-fold symmetry in ice crystals grown from water vapor (that is, snow flakes). Hexagonal ice (Space group P63/mmc, 194; symmetry D6h, Laue class symmetry 6/mmm; analogous to β-tridymite silica or lonsdaleite) possesses a fairly open low-density structure, where the packing efficiency is low (~1/3) compared with simple cubic (~1/2) or face centered cubic (~3/4) structuresa (and in contrast to face centered cubic close packed solid hydrogen sulfide). The crystals may be thought of as consisting of sheets lying on top of each other. The basic structure consists of a hexameric box where planes consist of chair-form hexamers (the two horizontal planes, opposite) or boat-form hexamers (the three vertical planes, opposite). In this diagram the hydrogen bonding is shown ordered whereas in reality it is random,b as protons can move between (ice) water molecules at temperatures above about 130 K [1504]. The water molecules have a staggered arrangement of hydrogen bonding with respect to three of their neighbors, in the plane of the chair-form hexamers. The fourth neighbor (shown as vertical links opposite) has an eclipsed arrangement of hydrogen bonding. There is a small deviation from ideal hexagonal symmetry as the unit cellc is 0.3 % shorter in the c- direction (in the direction of the eclipsed hydrogen bonding, shown as vertical links in the figures).
    [Show full text]
  • Ages of Large Lunar Impact Craters and Implications for Bombardment During the Moon’S Middle Age ⇑ Michelle R
    Icarus 225 (2013) 325–341 Contents lists available at SciVerse ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus Ages of large lunar impact craters and implications for bombardment during the Moon’s middle age ⇑ Michelle R. Kirchoff , Clark R. Chapman, Simone Marchi, Kristen M. Curtis, Brian Enke, William F. Bottke Southwest Research Institute, 1050 Walnut Street, Suite 300, Boulder, CO 80302, United States article info abstract Article history: Standard lunar chronologies, based on combining lunar sample radiometric ages with impact crater den- Received 20 October 2012 sities of inferred associated units, have lately been questioned about the robustness of their interpreta- Revised 28 February 2013 tions of the temporal dependance of the lunar impact flux. In particular, there has been increasing focus Accepted 10 March 2013 on the ‘‘middle age’’ of lunar bombardment, from the end of the Late Heavy Bombardment (3.8 Ga) until Available online 1 April 2013 comparatively recent times (1 Ga). To gain a better understanding of impact flux in this time period, we determined and analyzed the cratering ages of selected terrains on the Moon. We required distinct ter- Keywords: rains with random locations and areas large enough to achieve good statistics for the small, superposed Moon, Surface crater size–frequency distributions to be compiled. Therefore, we selected 40 lunar craters with diameter Cratering Impact processes 90 km and determined the model ages of their floors by measuring the density of superposed craters using the Lunar Reconnaissance Orbiter Wide Angle Camera mosaic. Absolute model ages were computed using the Model Production Function of Marchi et al.
    [Show full text]