Twar: Introducing a Method to Actually Calculate Wins Above Replacement
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Detroit Tigers Game Notes
DETROIT TIGERS GAME NOTES WORLD SERIES CHAMPIONS: 1935, 1945, 1968, 1984 Detroit Tigers Media Rela ons Department • Comerica Park • Phone (313) 471-2000 • Fax (313) 471-2138 • Detroit, MI 48201 www. gers.com • @ gers, @TigresdeDetroit, @DetroitTigersPR Detroit Tigers (9-14-4) at Philadelphia Phillies (10-15-1) Thursday, March 22, 2018 • Spectrum Field, Clearwater, FL • 1:05 p.m. ET LHP MaƩ hew Boyd (3-0, 4.50) vs. RHP Jake Arrieta (No Record) TV: MLB.TV • Radio: None RECENT RESULTS: The Tigers dropped a 3-2 decision to the Atlanta Braves on Wednesday night at Champion NUMERICAL ROSTER Stadium in Kissimmee. Mikie Mahtook belted a solo home run, his fi rst of the spring, while Niko Goodrum, 1 José Iglesias INF Leonys Mar n, Victor Reyes and Ronny Rodriguez each went 1x3 in the loss. Francisco Liriano started for 8 Mikie Mahtook OF Detroit, allowing two runs on four hits with fi ve walks and four strikeouts in 5.0 innings. Chad Bell and Drew 9 Nicholas Castellanos OF VerHagen each pitched a scoreless inning in relief with one strikeout. Warwick Saupold took the loss a er 12 Leonys Mar n OF giving up one run on one hit with one walk and one strikeout in 1.0 inning. The Tigers remain on the road 14 Alexi Amarista INF today as they travel to Clearwater to face the Philadelphia Phillies. 21 JaCoby Jones OF 22 Victor Reyes OF 24 Miguel Cabrera INF ROSTER MOVES: Prior to today's game, the Tigers announced the following roster moves: 27 Jordan Zimmermann RHP - Op oned LHP's Chad Bell and Blaine Hardy to Triple A Toledo 30 Alex Wilson RHP - Reassigned -

Today's Starting Lineups
BOSTON RED SOX (62-39) vs. TORONTO BLUE JAYS (49-47) Tuesday, July 27, 2021 ● Fenway Park, Boston, MA TORONTO BLUE JAYS AVG HR RBI PLAYER POS 1 2 3 4 5 6 7 8 9 10 11 12 AB R H RBI .236 8 15 4-George Springer CF .328 32 80 27-Vladimir Guerrero Jr. 1B .275 24 62 10-Marcus Semien 2B .296 18 67 11-Bo Bichette SS .296 15 59 37-Teoscar Hernández DH .263 11 41 13-Lourdes Gurriel Jr. LF .256 18 63 15-Randal Grichuk RF .220 7 25 8-Cavan Biggio L 3B .255 3 8 30-Alejando Kirk C R H E LOB PITCHERS DEC IP H R ER BB SO HR WP HB P/S GAME DATA 38-Robbie Ray, LHP (8-5, 3.12) Official Scorer: Loren Foxx 1st Pitch: Temp: Game Time: Attendance: 4-George Springer, OF 19-Dave Hudgens (Bench) 38-Robbie Ray, LHP 68-Jordan Romano, RHP TOR Bench TOR Bullpen 5-Santiago Espinal, INF 20-Luis Rivera (Third Base) 39-Kirby Yates, RHP^ 69-Tommy Milone, LHP^ 6-Alek Manoah, RHP* 22-Steven Matz, LHP 40-Peter Walker (Pitching) 74-Breyvic Valera, INF (S) Left Left 7-Reese McGuire, C (L) 25-Charlie Montoyo (Manager) 41-Rafael Dolis, RHP 90-Adam Cimber, RHP 7-Reese McGuire 52-Tayler Saucedo 8-Cavan Biggio, INF (L) 26-Matt Buschmann (Bullpen) 48-Ross Stripling, RHP 99-Hyun Jin Ryu, LHP 56-Ryan Borucki 9-Danny Jansen, C* 27-Vladimir Guerrero Jr., INF 52-Tayler Saucedo, LHP Right 58-Tim Mayza 10-Marcus Semien, INF 30-Alejando Kirk, C 53-Mark Budzinski (First Base) * 10-day IL 5-Santiago Espinal 60-Kirby Snead 11-Bo Bichette, INF 31-Thomas Hatch, RHP 56-Ryan Borucki, LHP ^ 60-day IL 13-Lourdes Gurriel Jr., OF 33-Trevor Richards, RHP 57-Trent Thornton, RHP #COVID-19 Related IL Switch Right 14-Corey Dickerson, OF (L)* 34-Tyler Chatwood, RHP* 58-Tim Mayza, LHP 15-Randal Grichuk, OF 35-David Phelps, RHP^ 60-Kirby Snead, LHP 74-Breyvic Valera 33-Trevor Richards 17-John Schneider (Coach) 36-A.J. -

Boston Red Sox 5, New York Yankees 3
WORLD SERIES CHAMPIONS (9): 1903, 1912, 1915, 1916, 1918, 2004, 2007, 2013, 2018 AMERICAN LEAGUE CHAMPIONS (14): 1903, 1904, 1912, 1915, 1916, 1918, 1946, 1967, 1975, 1986, 2004, 2007, 2013, 2018 AMERICAN LEAGUE EAST DIVISION CHAMPIONS (10): 1975, 1986, 1988, 1990, 1995, 2007, 2013, 2016, 2017, 2018 AMERICAN LEAGUE WILD CARD (7): 1998, 1999, 2003, 2004, 2005, 2008, 2009 @BOSTONREDSOXPR • HTTP://PRESSROOM.REDSOX.COM • @SOXNOTES BOSTON RED SOX 5, NEW YORK YANKEES 3 Friday, June 25, 2021 • Fenway Park, Boston, MA 1 2 3 4 5 6 7 8 9 R H E PITCH COUNTS New York 0 3 0 0 0 0 0 0 0 3 9 2 RED SOX Boston 3 0 1 0 0 0 0 1 X 5 7 1 Pitcher # (Strikes) Win: Whitlock (3-1) Loss: Germán (4-5) Save: Barnes (16) Martín Pérez 67 (44) Time of Game: 3:37 Attendance: 36,869 (1st sellout) Weather: 66°, E at 6 mph Hirokazu Sawamura 20 (10) Yankees HR: None Garrett Whitlock 33 (21) Adam Ottavino 13 (10) Red Sox HR: None Matt Barnes 19 (14) YANKEES RED SOX NOTES (45-31) Pitcher # (Strikes) Domingo Germán 72 (46) THE RED SOX are 4-0 vs. NYY this season, out-scoring the Yankees, 23-13, during the season series. Lucas Luetge 40 (19) Jonathan Loaisiga 21 (15) Are 3-4 in their last 7 games, but 13-8 in their last 21...Are 21-14 at home since getting swept by BAL to begin the season. Zack Britton 11 (7) 4 Sox relievers combined to toss 5.1 scoreless innings: Sawamura (1.1 IP), Whitlock (2.0), Ottavino (1.0), and Barnes (1.0). -

November, 2006
By the Numbers Volume 16, Number 4 The Newsletter of the SABR Statistical Analysis Committee November, 2006 Review Academic Research: Errors and Official Scorers Charlie Pavitt The author describes a recent academic study investigating the change in error rates over time, and speculating on the role of the official scorer in the “home field advantage” for errors. This is one of a series of reviews of sabermetric articles published in academic journals. It is part of a project of mine to collect and catalog sabermetric research, and I would appreciate learning of and receiving copies of any studies of which I am unaware. Please visit the Statistical Baseball Research Bibliography at www.udel.edu/communication/pavitt/biblioexplan.htm . Use it for your research, and let me know what is missing. per game, used as a proxy for team speed, were positively related David E. Kalist and Stephen J. Spurr, Baseball with errors; others have previously noticed the speed/error Errors, Journal of Quantitative Analysis in association. Sports, Volume 2, Issue 4, Article 3 Interestingly, the National League has consistently “boasted” more errors than the American League; the authors are unsure In its short existence, JQAS has shown a tendency to present why, but comparisons both before and after the appearance of the articles that are long on method but short on interesting designated hitter in the junior circuit indicate that this is probably substance (case in point, another piece in Volume 2 Issue 4 not the reason. relevant to the tired old topic of within-league parity). Kalist and Spurr’s effort is a welcome change. -

San Francisco Giants
SAN FRANCISCO GIANTS 2016 END OF SEASON NOTES 24 Willie Mays Plaza • San Francisco, CA 94107 • Phone: 415-972-2000 sfgiants.com • sfgigantes.com • sfgiantspressbox.com • @SFGiants • @SFGigantes • @SFG_Stats THE GIANTS: Finished the 2016 campaign (59th in San Francisco and 134th GIANTS BY THE NUMBERS overall) with a record of 87-75 (.537), good for second place in the National NOTE 2016 League West, 4.0 games behind the first-place Los Angeles Dodgers...the 2016 Series Record .............. 23-20-9 season marked the 10th time that the Dodgers and Giants finished in first and Series Record, home ..........13-7-6 second place (in either order) in the NL West...they also did so in 1971, 1994 Series Record, road ..........10-13-3 (strike-shortened season), 1997, 2000, 2003, 2004, 2012, 2014 and 2015. Series Openers ...............24-28 Series Finales ................29-23 OCTOBER BASEBALL: San Francisco advanced to the postseason for the Monday ...................... 7-10 fourth time in the last sevens seasons and for the 26th time in franchise history Tuesday ....................13-12 (since 1900), tied with the A's for the fourth-most appearances all-time behind Wednesday ..................10-15 the Yankees (52), Dodgers (30) and Cardinals (28)...it was the 12th postseason Thursday ....................12-5 appearance in SF-era history (since 1958). Friday ......................14-12 Saturday .....................17-9 Sunday .....................14-12 WILD CARD NOTES: The Giants and Mets faced one another in the one-game April .......................12-13 wild-card playoff, which was added to the MLB postseason in 2012...it was the May .........................21-8 second time the Giants played in this one-game playoff and the second time that June ...................... -

Sabermetrics: the Past, the Present, and the Future
Sabermetrics: The Past, the Present, and the Future Jim Albert February 12, 2010 Abstract This article provides an overview of sabermetrics, the science of learn- ing about baseball through objective evidence. Statistics and baseball have always had a strong kinship, as many famous players are known by their famous statistical accomplishments such as Joe Dimaggio’s 56-game hitting streak and Ted Williams’ .406 batting average in the 1941 baseball season. We give an overview of how one measures performance in batting, pitching, and fielding. In baseball, the traditional measures are batting av- erage, slugging percentage, and on-base percentage, but modern measures such as OPS (on-base percentage plus slugging percentage) are better in predicting the number of runs a team will score in a game. Pitching is a harder aspect of performance to measure, since traditional measures such as winning percentage and earned run average are confounded by the abilities of the pitcher teammates. Modern measures of pitching such as DIPS (defense independent pitching statistics) are helpful in isolating the contributions of a pitcher that do not involve his teammates. It is also challenging to measure the quality of a player’s fielding ability, since the standard measure of fielding, the fielding percentage, is not helpful in understanding the range of a player in moving towards a batted ball. New measures of fielding have been developed that are useful in measuring a player’s fielding range. Major League Baseball is measuring the game in new ways, and sabermetrics is using this new data to find better mea- sures of player performance. -

2015 Playoff Contenders Baseball Group Break Team Checklist
2015 Playoff Contenders Baseball Group Break Team Checklist Card Pro Team Player Set Team Pictured # Assignment Grayson Long Prospect Ticket 49 Texas A&M Aggies Angels Jahmai Jones Draft Ticket 40 Los Angeles Angels Angels Matt Thaiss USA Baseball Tickets SP 56 USA College Angels Taylor Ward College Ticket 29 Fresno State Bulldogs Angels Taylor Ward Collegiate Connections Signatures 19 Fresno State Bulldogs Angels Taylor Ward USA Baseball Tickets 26 USA College Angels A.J. Reed Alumni Ink 1 Kentucky Wildcats Astros A.J. Reed Old School Colors Signatures 21 Kentucky Wildcats Astros Alex Bregman College Ticket 3 LSU Tigers Astros Alex Bregman Collegiate Connections Signatures 7 LSU Tigers Astros Alex Bregman School Colors Signatures 14 LSU Tigers Astros Alex Bregman USA Baseball Tickets SP 7 USA College Astros Brett Phillips Prospect Ticket SP 3 Houston Astros Astros Craig Biggio Alumni Ink 21 Seton Hall Pirates Astros Craig Biggio Old School Colors Signatures 4 Seton Hall Pirates Astros Daz Cameron Draft Ticket 2 Houston Astros Astros Daz Cameron USA Baseball Tickets 19 USA 18U Astros Kyle Tucker Draft Ticket 4 Houston Astros Astros Kyle Tucker USA Baseball Tickets SSP 32 USA 15U Astros Riley Ferrell College Ticket 23 TCU Horned Frogs Astros Riley Ferrell Collegiate Connections Signatures 15 TCU Horned Frogs Astros Riley Ferrell Collegiate Connections Signatures 16 TCU Horned Frogs Astros Riley Ferrell USA Baseball Tickets 14 USA College Astros Teoscar Hernandez Prospect Ticket 36 Houston Astros Astros A.J. Puk USA Baseball Tickets SP -
Baseball Record Book
2018 BASEBALL RECORD BOOK BIG12SPORTS.COM @BIG12CONFERENCE #BIG12BSB CHAMPIONSHIP INFORMATION/HISTORY The 2018 Phillips 66 Big 12 Baseball Championship will be held at Chickasaw Bricktown Ballpark, May 23-27. Chickasaw Bricktown Ballpark is home to the Los Angeles Dodgers Triple A team, the Oklahoma City Dodgers. Located in OKC’s vibrant Bricktown District, the ballpark opened in 1998. A thriving urban entertainment district, Bricktown is home to more than 45 restaurants, many bars, clubs, and retail shops, as well as family- friendly attractions, museums and galleries. Bricktown is the gateway to CHAMPIONSHIP SCHEDULE Oklahoma City for tourists, convention attendees, and day trippers from WEDNESDAY, MAY 23 around the region. Game 1: Teams To Be Determined (FCS) 9:00 a.m. Game 2: Teams To Be Determined (FCS) 12:30 p.m. This year marks the 19th time Oklahoma City has hosted the event. Three Game 3: Teams To Be Determined (FCS) 4:00 p.m. additional venues have sponsored the championship: All-Sports Stadium, Game 4: Teams To Be Determined (FCS) 7:30 p.m. Oklahoma City (1997); The Ballpark in Arlington (2002, ‘04) and ONEOK Field in Tulsa (2015). THURSDAY MAY 24 Game 5: Game 1 Loser vs. Game 2 Loser (FCS) 9:00 a.m. Past postseason championship winners include Kansas (2006), Missouri Game 6: Game 3 Loser vs. Game 4 Loser (FCS) 12:30 p.m. (2012), Nebraska (1999-2001, ‘05), Oklahoma (1997, 2013), Oklahoma Game 7: Game 1 Winner vs. Game 2 Winner (FCS) 4:00 p.m. State (2004, ‘17), TCU (2014, ‘16), Texas (2002-03, ‘08-09, ‘15), Texas Game 8: Game 3 Winner vs. -

2015 Topps Opening Day Baseball Checklist
BASE 1 Homer Bailey Cincinnati Reds ® 2 Curtis Granderson New York Mets ® 3 Todd Frazier Cincinnati Reds ® 4 Lonnie Chisenhall Cleveland Indians ® 5 Jose Altuve Houston Astros ® 6 Matt Carpenter St. Louis Cardinals ® 7 Matt Garza Milwaukee Brewers ™ 8 Starling Marte Pittsburgh Pirates ® 9 Yu Darvish Texas Rangers ® 10 Pat Neshek Houston Astros ® 11 Anthony Rizzo Chicago Cubs ® 12 Chris Tillman Baltimore Orioles ® 13 Drew Hutchison Toronto Blue Jays® 14 Michael Taylor Washington Nationals® Rookie 15 Gregory Polanco Pittsburgh Pirates® 16 Jake Lamb Arizona Diamondbacks ® Rookie 17 David Ortiz Boston Red Sox® 18 Pablo Sandoval Boston Red Sox ® 19 Adam Jones Baltimore Orioles ® 20 Miguel Cabrera Detroit Tigers ® 21 Evan Gattis Atlanta Braves™ 22 Gerrit Cole Pittsburgh Pirates ® 23 Greg Holland Kansas City Royals ® 24 Tim Lincecum San Francisco Giants ® 25 Jorge Soler Chicago Cubs® Rookie 26 Buster Posey San Francisco Giants ® 27 George Springer Houston Astros ® 28 Jedd Gyorko San Diego Padres ™ 29 John Lackey St. Louis Cardinals® 30 Danny Santana Minnesota Twins® 31 David Wright New York Mets ® 32 Jordan Zimmermann Washington Nationals ® 33 Eric Hosmer Kansas City Royals ® 34 Michael Pineda New York Yankees ® 35 Travis d'Arnaud New York Mets® 36 Clay Buchholz Boston Red Sox ® 37 Chris Archer Tampa Bay Rays ™ 38 Johnny Cueto Cincinnati Reds ® 39 Albert Pujols Angels ® 40 Clayton Kershaw Los Angeles Dodgers ® 41 Carlos Gonzalez Colorado Rockies ™ 42 Anthony Rendon Washington Nationals ® 43 Nick Castellanos Detroit Tigers ® 44 Jonathan Lucroy -

2010 Championship Game Notes Saturday, November 20, 2010 Media Relations CONTACTS: Paul Jensen (480/710-8201, [email protected]) Adam C
2010 Championship Game Notes Saturday, November 20, 2010 Media Relations CONTACTS: Paul Jensen (480/710-8201, [email protected]) Adam C. Nichols (617/448-1942, [email protected]) Pat Kurish (480/628-4446, [email protected]) Media Relations FAX: 602/681-9363 Website: www.mlbfallball.com Facebook: www.facebook.com/MLBFallBall Twitter: @MLBazFallLeague Arizona Fall League East Division Team W L Pct. GB Home Away Div. Streak Last 10 AFL Championship History Scottsdale Scorpions 20 12 .625 - 12-3 8-9 8-5 L1 6-4 2009 Phoenix Desert Dogs 4 Mesa Solar Sox 13 17 .433 6.0 8-7 5-10 3-8 L6 3-7 Peoria Javelinas 5 Phoenix Desert Dogs 11 17 .393 7.0 6-8 5-9 7-5 W3 5-5 2008 Mesa Solar Sox 4 Phoenix Desert Dogs 10 Arizona Fall League West Division 2007 Phoenix Desert Dogs 7 Team W L Pct. GB Home Away Div. Streak Last 10 Surprise Rafters 2 Peoria Javelinas 20 10 .667 - 10-5 10-5 8-4 W1 7-3 Surprise Rafters 17 12 .586 2.5 11-5 6-7 9-3 W4 6-4 2006 Grand Canyon Rafters 2 Phoenix Desert Dogs 6 Peoria Saguaros 9 22 .290 11.5 6-9 3-13 1-11 W1 2-8 2005 Surprise Scorpions 2 Phoenix Desert Dogs 6 AFL Championship Game First-Round Draft Picks The Championship Game will feature nine first-round picks between the teams 2004 Scottsdale Scorpions 2 nd 2B Dustin Ackley (SEA) 2 in ’09 Phoenix Desert Dogs 6 RHP Rex Brothers (COL) 34th in ‘09 2003 Mesa Solar Sox 7 OF Mike Burgess (WSH) 49th in ‘07 st Mesa Desert Dogs 2 IF Charlie Culberson (SF) 51 in ‘07 C Ed Easley (ARI) 61st in ‘07 2002 Peoria Javelinas 7 RHP Josh Fields (SEA) 20th in ‘08 Scottsdale Scorpions 1 IF Conor Gillaspie (SF) 37th in ‘08 OF Bryce Harper (WSH) 1st in ‘10 2001 Phoenix Desert Dogs 12 OF A.J. -
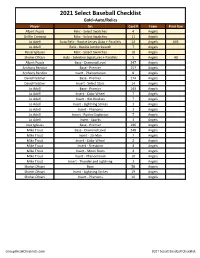
2021 Panini Select Baseball Checklist
2021 Select Baseball Checklist Gold=Auto/Relics Player Set Card # Team Print Run Albert Pujols Relic - Select Swatches 4 Angels Griffin Canning Relic - Select Swatches 11 Angels Jo Adell Auto Relic - Rookie Jersey Auto + Parallels 14 Angels 645 Jo Adell Relic - Rookie Jumbo Swatch 7 Angels Raisel Iglesias Relic - Select Swatches 18 Angels Shohei Ohtani Auto - Selective Signatures + Parallels 5 Angels 40 Albert Pujols Base - Diamond Level 247 Angels Anthony Rendon Base - Premier 157 Angels Anthony Rendon Insert - Phenomenon 8 Angels David Fletcher Base - Premier 174 Angels David Fletcher Insert - Select Stars 14 Angels Jo Adell Base - Premier 143 Angels Jo Adell Insert - Color Wheel 7 Angels Jo Adell Insert - Hot Rookies 7 Angels Jo Adell Insert - Lightning Strikes 1 Angels Jo Adell Insert - Phenoms 3 Angels Jo Adell Insert - Rookie Explosion 7 Angels Jo Adell Insert - Sparks 1 Angels Jose Iglesias Base - Premier 196 Angels Mike Trout Base - Diamond Level 248 Angels Mike Trout Insert - 25-Man 7 Angels Mike Trout Insert - Color Wheel 2 Angels Mike Trout Insert - Firestorm 4 Angels Mike Trout Insert - Moon Shots 4 Angels Mike Trout Insert - Phenomenon 10 Angels Mike Trout Insert - Thunder and Lightning 3 Angels Shohei Ohtani Base 58 Angels Shohei Ohtani Insert - Lightning Strikes 19 Angels Shohei Ohtani Insert - Phenoms 10 Angels GroupBreakChecklists.com 2021 Select Baseball Checklist Player Set Card # Team Print Run Abraham Toro Relic - Select Swatches 1 Astros Alex Bregman Auto - Moon Shot Signatures + Parallels 2 Astros 102 Bryan Abreu -

Links to Recen
Navigation: Jump to content areas:Network Bar & Login Section Navigation Main Blog Content Secondary Sidebar: Links to Recent Stories, FanPosts plus FanShots Masthead The Coyotes news is a mini light right now given that everyone has scattered to the four winds and it is a holiday weekend.12.00 Normal 0 artificial artificial pretended EN-US X-NONE X-NONE Coyotes NewsNo Owner, No Problem? Coyotes Players plus Staff Feel Confident Team Will Return - Five For HowlingJordan reviews the latest in the ownership anecdote.I Freaking Love the Vrb! | The Good, The Bad, The CoyotesYotesgurl aboard #17.The.end | The Checking LineA discern behind at the Coyotes 2010-11 roster.Phoenix Coyotes' Ilya Bryzgalov is no fan of WinnipegRehashing of Bryz's comments from earlier among the week.Series Review: Detroit Red Wings Vs,new nfl jersey. Phoenix Coyotes - SB Nation DetroitIf you absence to relive the horror click the link.Column: Coyotes ought stayThe issue is almost ownership,2012 nike jerseys. I couldn't accede more. (s/t The Yotes Diva)Brownie Points: Hockey wants team surrounded Arizona - East Valley Tribune: SportsJerry Brown thinks the Dogs are staying.More links afterward the bound.News From Around the Hockey WorldKings at Sharks - 04/23/2011 - NHL.com - RecapJonathan Quick lingered busy within the Kings 3-1 win over the Sharks.Nathan Horton lifts Bruins to 2-1 win among double OT to take Game five - Stanley Cup of ChowderBruins take the series adviser.Recap: Capitals 3 Rangers 1 - Japers' RinkCaps clinch the order.ECQF Game five recap: Tampa Bay Lightning five at Pittsburgh Penguins four - Raw ChargeThe Lightning guilt explodes within Pittsburgh.