Competent Goalie Evaluation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Injuries Continue to Plague Jets Seven Wounded Players Missed Saturday's Game
Winnipeg Free Press https://www.winnipegfreepress.com/sports/hockey/jets/injuries-continue-to-keep-jets-in-sick- bay-476497963.html?k=QAPMqC Injuries continue to plague Jets Seven wounded players missed Saturday's game By: Mike McIntyre WASHINGTON — Is there a doctor in the house? It’s been a common refrain for the Winnipeg Jets lately, as they just can’t seem to get close to a full, healthy lineup. Seven players were out due to injury in Saturday’s 2-1 loss in Philadelphia. Here’s what we know about all of them, with further updates expected today as the Jets return to action with a morning skate and then their game in Washington against the Capitals. Mark Scheifele has missed two games with a suspected shoulder injury, and there will be no rushing him back into action. He’s considered day-to-day at this point, and coach Paul Maurice had said last week he was a possibility to play either tonight, or tomorrow in Nashville. But don’t bet on it. Defenceman Toby Enstrom is battling a lower-body issue which kept him out for four games, saw him return in New Jersey last Thursday and then be back out on Saturday. Maurice said it’s a nagging thing that can change day-to-day, so his status is very much a question mark. Defenceman Dmitry Kulikov missed Saturday’s game after getting hurt Thursday in New Jersey. Maurice hasn’t said how long he could be out, only that it’s upper-body. Goalie Steve Mason has been sent back to Winnipeg for further testing on a lower-body injury he suffered late in the game against the New York Rangers last Tuesday, which was his first game back from his second concussion of the season. -

Youngblood Hockey
Youngblood Hockey `2015 NHL Draft Guide @RossyYoungblood @RossyYoungblood YOUNGBLOOD HOCKEY The Starting Lineup Top 150 Player Rankings 3 The player rankings are broken down loosely into talent tiers. With each changing colour, a new tier of players starts. Top 60 Prospect Profiles 8 The “Style Comparison” column is a fun addition to attempt to compare a prospects playing style to a current/past NHLer. It does not indicate that the prospect will have a similar career or be as successful as their comparable. Mock Draft (Three Round) 30 Categorical Rankings 36 2016 NHL Draft Ranking 38 2017 NHL Draft – Watch List 38 Acknowledgements and Stick Taps 39 2 @RossyYoungblood 1. Connor McDavid, LC (Erie, OHL) 2. Jack Eichel, RC (Boston University, Hockey East) 3. Mitch Marner, RW (London, OHL) 4. Noah Hanifin, D (Boston College, Hockey East) 5. Dylan Strome, LC (Erie, OHL) 6. Pavel Zacha, LC (Sarnia, OHL) 7. Lawson Crouse, LW (Kingston, OHL) 8. Ivan Provorov, LD (Brandon, WHL) 9. Mathew Barzal, RC (Seattle, WHL) 10. Zach Werenski, D (University of Michigan, Big Ten) 11. Mikko Rantanen, RW (TPS, Liiga) 12. Kyle Connor, LW (Youngstown, USHL) 13. Timo Meier, RW (Halifax, QMJHL) 14. Denis Guryanov, RW, Toglilatti 2 (MHL) Pavel Zacha has tons of growth left to his game and all the pro tools to become an impact top line player. 15. Travis Konecny, RW (Ottawa, OHL) 16. Nicholas Merkley, C (Kelowna, WHL) 17. Jeremy Bracco, RW (US NTDP, USHL) There's no debate who will be selected 1st overall but 18. Evgeny Svechnikov, RW (Cape Breton, QMJHL) both McDavid and Eichel stand to be franchise 19. -

Columbus Blue Jackets Defenseman Zach Werenski
FOR IMMEDIATE RELEASE: APRIL 20, 2017 COLUMBUS BLUE JACKETS DEFENSEMAN ZACH WERENSKI NAMED A FINALIST FOR CALDER MEMORIAL TROPHY Werenski joins Toronto’s Auston Matthews and Winnipeg’s Patrik Laine as finalists for top rookie award COLUMBUS, OHIO --- Columbus Blue Jackets defenseman Zach Werenski is among three finalists for the Calder Memorial Trophy, given annually to the National Hockey League’s most outstanding rookie as voted on by the Professional Hockey Writers’ Association, the club and NHL announced tonight. Center Auston Matthews of the Toronto Maple Leafs and right wing Patrik Laine of the Winnipeg Jets are the other two finalists. Werenski, 19, led all rookie NHL defensemen in scoring with 11 goals and 36 assists for 47 points with 14 penalty minutes and a +17 plus/minus rating in 78 games this season. His point total also stood seventh in overall rookie scoring, was 13th among all NHL defensemen, set a franchise record for points by a rookie and was the second-highest total by a blueliner in club history (51-James Wisniewski, 2013-14). Historically, he tallied the sixth-most points by a teenage rookie defenseman in NHL history. Columbus’ first pick, eighth overall, in the 2015 NHL Draft, Werenski played two seasons at the University of Michigan from 2014-16 before joining the Lake Erie Monsters, the Blue Jackets’ American League affiliate, in April 2016. He tallied 5-9-14 in 17 playoff games, recording the most assists and points by an 18-year-old in the history of the Calder Cup Playoffs. He finished second among AHL defensemen in playoff scoring to help the Monsters capture the Calder Cup championship. -
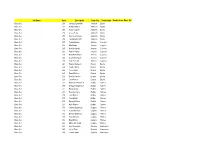
Set Name Card Description Team City Team Name Rookie Auto
Set Name Card Description Team City Team Name Rookie Auto Mem #'d Base Set 251 Hampus Lindholm Anaheim Ducks Base Set 252 Rickard Rakell Anaheim Ducks Base Set 253 Sami Vatanen Anaheim Ducks Base Set 254 Corey Perry Anaheim Ducks Base Set 255 Antoine Vermette Anaheim Ducks Base Set 256 Jonathan Bernier Anaheim Ducks Base Set 257 Tobias Rieder Arizona Coyotes Base Set 258 Max Domi Arizona Coyotes Base Set 259 Alex Goligoski Arizona Coyotes Base Set 260 Radim Vrbata Arizona Coyotes Base Set 261 Brad Richardson Arizona Coyotes Base Set 262 Louis Domingue Arizona Coyotes Base Set 263 Luke Schenn Arizona Coyotes Base Set 264 Patrice Bergeron Boston Bruins Base Set 265 Tuukka Rask Boston Bruins Base Set 266 Torey Krug Boston Bruins Base Set 267 David Backes Boston Bruins Base Set 268 Dominic Moore Boston Bruins Base Set 269 Joe Morrow Boston Bruins Base Set 270 Rasmus Ristolainen Buffalo Sabres Base Set 271 Zemgus Girgensons Buffalo Sabres Base Set 272 Brian Gionta Buffalo Sabres Base Set 273 Evander Kane Buffalo Sabres Base Set 274 Jack Eichel Buffalo Sabres Base Set 275 Tyler Ennis Buffalo Sabres Base Set 276 Dmitry Kulikov Buffalo Sabres Base Set 277 Kyle Okposo Buffalo Sabres Base Set 278 Johnny Gaudreau Calgary Flames Base Set 279 Sean Monahan Calgary Flames Base Set 280 Dennis Wideman Calgary Flames Base Set 281 Troy Brouwer Calgary Flames Base Set 282 Brian Elliott Calgary Flames Base Set 283 Micheal Ferland Calgary Flames Base Set 284 Lee Stempniak Carolina Hurricanes Base Set 285 Victor Rask Carolina Hurricanes Base Set 286 Jordan -

1 Columbus Blue Jackets News Clips July 25-27, 2020 Columbus Blue
Columbus Blue Jackets News Clips July 25-27, 2020 Columbus Blue Jackets PAGE 02: Columbus Dispatch: Four Blue Jackets had `normal’ time off in native Sweden PAGE 04: Columbus Dispatch: Columbus Blue Jackets’ Nathan Gerbe still proving himself PAGE 05: The Athletic: Blue Jackets unsettled, Tortorella irritated, as training camp 2.0 nears end PAGE 08: Sportsnet.ca: Tortorella calls out ‘key people’ as Maple Leafs showdown looms PAGE 11: Columbus Dispatch: Blue Jackets still have lineup decisions to make PAGE 12: Columbus Dispatch: Coach John Tortorella wonders if Columbus Blue Jackets are prepared for series PAGE 14: Columbus Dispatch: Columbus Blue Jackets’ Dubois, Wennberg differ in personality Cleveland Monsters/Prospects NHL/Websites PAGE 16: The Athletic: ‘We don’t expect it to be perfect’: Updates on the NHL’s health and safety plans PAGE 18: The Athletic: What will happen to the NHL playoff handshake line during the pandemic? PAGE 19: The Athletic: ‘To be united is important’ – Inside the NHL’s plan to address racism PAGE 24: Sportsnet.ca: Inside the NHL's incredible effort to ensure the show goes on PAGE 26: Sportsnet.ca: Five stats-based predictions for the 2020 Stanley Cup Playoffs PAGE 29: Sportsnet.ca: Quick Shifts: 'Wild card' Nick Robertson pushes fate to the wire PAGE 35: The Athletic: NHL players share pandemic tales of personal and financial stress PAGE 41: Sportsnet.ca: NHL Playoff Primer: Everything you need to know ahead of post-season PAGE 43: Sportsnet.ca: NHL teams arrive in Toronto, Edmonton ahead of league restart 1 Columbus Dispatch / Four Blue Jackets had `normal’ time off in native Sweden By Adam Jardy – July 25, 2020 The indefinite suspension of the NHL season in March presented choices for the five Swedish players who were with the Blue Jackets at the time. -

Jääkiekon Mm U20 Tshekki
JÄÄKIEKON 26.12.2015 - 5.1.2016 MM U20 TÄMÄ UUSIKSI! Kisojen kaikki ottelut Tulos- ja Pitkävedossa sekä Live-vedossa. Tärkeässä roolissa. Kiitos Veikkauksen pelien pelaajat! ”Jääkiekko on Suomen seuratuin laji ja Leijonat kuin vaikkapa tilastonikkarit, jokaiselle löytyy Suomen suosituin joukkue. Leijonien ja Nuor- oma ruutunsa jos intoa piisaa. Onnistumisen ten Leijonien menestystä arvoturnauksissa elämyksiä ja ilon tunteita voi kokea myös jään jännitetään silmä kovana niin mediassa kuin laidalla. kotisohvilla ympäri maan. Valtion Jääkiekkoliitolle maksama tuki tulee Lajin harrastaminen alkaa seurojen järjestä- kokonaisuudessaan Veikkauksen tuotosta. mistä kiekkokouluista ja voi parhaimmillaan Tämä mahdollistaa lajin pyörittämisen ja erityi- jatkua läpi elämän - siinä missä lahjakkaimmat sesti lasten ja nuorten jääkiekon harrastamisen pelaajat saavat jääkiekosta ammatin, on laji koko maan laajuisesti. useimmille elämänmittainen tapa liikkua ja viettää aikaa hyvien ystävien kanssa. Nuorille Lämmin kiitos kaikille Veikkauksen pelien pe- jääkiekko tarjoaa turvallisen kasvuympäristön: laajille! ” Joukkueessa toimiminen kartuttaa taitoja, joilla pärjää myös kaukalon ulkopuolella. Matti Nurminen Ja toki jääkiekkoa voi harrastaa myös pelaa- matta: mukaan seuratoimintaan ovat tervetul- Toimitusjohtaja leita niin tuomarit, huoltajat, makkaranmyyjät Suomen Jääkiekkoliitto ry Liikunnalle miljoonaa euroa vuoden jokaisena 3 viikkona. OHJELMA & KERTOIMET JÄÄKIEKON MM U20 Kaikkien aikojen kultasauma? Alle 20-vuotiaiden MM-kisat on näköisenä Suomen menestystä -

Press Clips March 3, 2020
Buffalo Sabres Daily Press Clips March 3, 2020 Eichel and the Sabres visit the Jets Associated Press March 2, 2020 Buffalo Sabres (29-28-8, sixth in the Atlantic Division) vs. Winnipeg Jets (33-28-6, fifth in the Central Division) Winnipeg, Manitoba; Tuesday, 8 p.m. EST BOTTOM LINE: Jack Eichel leads Buffalo into a matchup against Winnipeg. He ranks 10th in the league with 77 points, scoring 35 goals and recording 42 assists. The Jets are 17-14-3 on their home ice. Winnipeg has scored 39 power-play goals, converting on 19.7% of chances. The Sabres are 10-18-4 in road games. Buffalo has scored 36 power-play goals, converting on 19.6% of chances. Buffalo took down Winnipeg 2-1 in the last meeting between these teams on Feb. 23. Kyle Okposo scored two goals for the Sabres in the win. TOP PERFORMERS: Kyle Connor leads the Jets with 33 goals and has totaled 67 points. Mark Scheifele has five goals and six assists over the last 10 games for Winnipeg. Eichel leads the Sabres with 42 total assists and has recorded 77 points. Okposo has four goals and two assists over the last 10 games for Buffalo. LAST 10 GAMES: Sabres: 5-5-0, averaging 3.1 goals, 5.3 assists, 1.8 penalties and 3.6 penalty minutes while giving up 2.9 goals per game with a .906 save percentage. Jets: 4-5-1, averaging 2.8 goals, 5.1 assists, 2.9 penalties and eight penalty minutes while giving up 2.5 goals per game with a .920 save percentage. -

BSV Bern Wacker Thun
22 Donnerstag, 6. Dezember 2018 Sport Nachrichten YB-Stürmer für den FCZ Fussball Per sofort wechselt Stür- mer Yann Kasai von den Young Boys zum FCZ. Der 20-jährige schweiz-kongolesische Doppel- bürgerkam in dieserSaisonvoral- lem bei der U-21 der Berner zum Einsatz und erzielte in 14 Spielen 13Tore.Erstammt aus dem Nach- wuchs von Xamax. Bei YB hätte es derjungeAngreiferangesichts der starken Konkurrenz schwer ge- habt, sich durchzusetzen. (red) Der erste Österreicher Fussball Ralph Hasenhüttl schaff- te als erster österreichischer Trai- ner den Sprung in die englische Premier-League. Der 51-jährige Steirer wird bei Southampton Nachfolgervon Mark Hughes.(sda) England, Premier League: Burnley - Liverpool (mit Shaqiri, Tor zum 1:3) 1:3. Everton - New- castle (mit Schär) 1:1. Fulham - Leicester 1:1. Wolverhampton - Chelsea 2:1. Tottenham - Southampton 3:1. Manchester United - Arsenal (ab 36. mit Lichtsteiner) 2:2. – Spitze: 1. Manchester City 15/41. 2. Liverpool 15/39. 3. Tottenham 15/33. Frankreich, Ligue 1: Bordeaux - Saint-Etienne Patrik Laine schiesst viele Tore und ist bei den Winnipeg Jets entsprechend Publikumsliebling. Foto: Vorname Name (XYZ, Agentur) 3:2. Caen - Nîmes 1:2. Dijon - Guingamp 2:1. Lyon - Rennes 0:2. Nantes - Marseille 3:2. Reims - Toulouse (mit Moubandje) 0:1. Strasbourg - Paris 1:1. – Spitze: 1. Paris Saint-Germain 16/44. So etwas kann nur er! 2. Lille 16/30. 3. Montpellier 16/29. Boltshauser fällt aus Eishockey Der erst 20-jährige Patrik Laine ist bester Torschütze der NHL und bunter Hund in der stets sterileren Eishockey Luca Boltshauser (25) Liga. Er steht aber auch als Paradebeispiel für Finnlands Ausbildung, in der sich Junge entfalten dürfen. -

2021 Nhl Awards Presented by Bridgestone Information Guide
2021 NHL AWARDS PRESENTED BY BRIDGESTONE INFORMATION GUIDE TABLE OF CONTENTS 2021 NHL Award Winners and Finalists ................................................................................................................................. 3 Regular-Season Awards Art Ross Trophy ......................................................................................................................................................... 4 Bill Masterton Memorial Trophy ................................................................................................................................. 6 Calder Memorial Trophy ............................................................................................................................................. 8 Frank J. Selke Trophy .............................................................................................................................................. 14 Hart Memorial Trophy .............................................................................................................................................. 18 Jack Adams Award .................................................................................................................................................. 24 James Norris Memorial Trophy ................................................................................................................................ 28 Jim Gregory General Manager of the Year Award ................................................................................................. -

Cam Atkinson, Seth Jones, Daniil Tarasov, Joonas Korpisalo
2020 COLUMBUS BLUE JACKETS 2021 ROW 1: ELVIS MERZLIKINS, MATISS KIVLENIEKS, BOONE JENNER, HEAD COACH JOHN TORTORELLA, DIRECTOR OF PLAYER PERSONNEL CHRIS CLARK, PRESIDENT MIKE PRIEST, MAJORITY OWNER JOHN P. MCCONNELL, GENERAL MANAGER JARMO KEKALAINEN, ASSISTANT GENERAL MANAGER BASIL MCRAE, ASSISTANT GENERAL MANAGER JOSH FLYNN, CAM ATKINSON, SETH JONES, DANIIL TARASOV, JOONAS KORPISALO ROW 2: VIDEO ASSISTANT COACH DAN SINGLETON, ASSISTANT COACH KENNY MCCUDDEN, GOALTENDING COACH MANNY LEGACE, ASSISTANT COACH BRAD LARSEN, MAX DOMI, MICHAEL DEL ZOTTO, ZACH WERENSKI, PATRIK LAINE, OLIVER BJORKSTRAND, JACK ROSLOVIC, GUS NYQUIST, ASSISTANT DEVELOPMENT COACH JARED BOLL, ASSISTANT COACH BRAD SHAW, SPECIAL ASSISTANT TO THE GENERAL MANAGER RICK NASH ROW 3: NATHAN GERBE, ALEXANDRE TEXIER, VLADISLAV GAVRIKOV, ERIC ROBINSON, SCOTT HARRINGTON, KEVIN STENLUND, GABRIEL CARLSSON, RYAN MACINNIS, MIKHAIL GRIGORENKO, STEFAN MATTEAU, DEAN KUKAN, ZAC DALPE, MIKKO LEHTONEN ROW 4: EQUIPMENT MANAGER TIM LEROY, ASSISTANT EQUIPMENT MANAGER JAMIE HEALY, ASSISTANT EQUIPMENT MANAGER JASON STYPINSKI, STRENGTH & CONDITIONING COACH KEVIN COLLINS, EMIL BEMSTROM, KOLE SHERWOOD, LIAM FOUDY, ANDREW PEEKE, GAVIN BAYREUTHER, ADAM CLENDENING, HEAD ATHLETIC TRAINER MIKE VOGT, ASSISTANT ATHLETIC TRAINER CHRIS STRICKLAND, DIRECTOR OF HIGH PERFORMANCE NELSON AYOTTE, ASSISTANT ATHLETIC TRAINER NATES GOTO 2021 CBJ SEASON IN REVIEW GUIDE // BLUEJACKETS.COM TABLE OF CONTENTS Table of Contents............................................................................1 Elvis Merzlikins -

Aho, Laine Ja Puljujärvi Nähdään Elokuussa Oulussa, Ensi Vuonna Raumalla
Aho, Laine ja Puljujärvi nähdään elokuussa Oulussa, ensi vuonna Raumalla JUTUT – 30.06.2017 klo 21:51 — Kimmo Mäkeläinen Sebastian Aho on nähty Äijänsuolla viimeksi helmikuussa 2016. Kuva: Pekka Lehmuskallio Liiga Alumni ja Oulun Kärpät järjestävät elokuussa hyväntekeväisyystapahtuman, jota tähdittävät lukuisat entiset ja nykyiset NHL-pelaajat. Raksilan jäällä nähdään tuolloin esimerkiksi Patrik Laine, Sebastian Aho, Jesse Puljujärvi, Jari Kurri ja Veli-Pekka Ketola. – Silloin saattaa olla mahdollista nähdä Patrik Laine ja Teemu Selänne samassa joukkueessa, Alumnin Tukisäätiön puheenjohtaja Juha Rantasila vihjaa. Tapahtumasta on tarkoitus tehdä vuosittainen. Ajankohta osuu jatkossakin elokuun kahdelle ensimmäiselle viikolle, ennen kuin NHL-pelaajat ovat lähteneet takaisin Pohjois-Amerikkaan. Tänä vuonna pelataan Oulussa, mutta Rantasilan mukaan vuoden päästä on Rauman vuoro. Tapahtuman ajankohdaksi on kaavailtu Pitsiturnauksen jälkeistä lauantaita. Rantasila teki merkittävän pelaajauran, sillä hänen mukaansa on nimetty jopa palkinto, joka liigakauden päätteeksi annetaan runkosarjassa eniten maaleja tehneelle puolustajalle. Porilaispelaaja saavutti Karhujen ja HIFK:n paidassa yhteensä kahdeksan SM-mitalia, joista puolet oli kultaisia. Hän pelasi 116 A-maaottelua, edusti Suomea viidesti MM- kisoissa ja kahdesti olympialaisissa. Rantasilan ansiot kaukalossa tiedetään ja muistetaan, mutta hänen kädenjälkensä jääkiekkoilun taustoissa ei ole yhtä laajalle levinnyttä kansantietoa. Hän on yksi Pelaajayhdistyksen eli Suomen Jääkiekkoilijat ry:n -

Lataa Tappara Kausijulkaisu 2020-2021 Tästä
Kausijulkaisu 2020-2021 TAPPARA Siperiasta palasi tyytyväinen Peltola s. 14 Domi on taas kotona ja kaikki hyvin s. 18 Hakametsän huima historia s. 4 Tshekkikolmikko on Tapparassa kuin kotonaan s. 20 2 Tappara Kausijulkaisu 2020–2021 PÄÄKIRJOITUS Hakametsä – Meidän Koti vuodesta 1965 ampereen kaupungin vanhempi tapparalainen meisien hetkien voittomaalil- kossa ja Erkki Lehtosessa, tulevaisuudesta. Tässä vai- Tpäättäjät ovat vuosikym- muistaa Tapparan nousun ta- laan Tapparalle mestaruu- maalintekotaito Jukka Alku- heessa on jo selvää, että Ha- menten saatossa osanneet kaisin jääkiekon huipulle kol- den. lassa ja Timo Sudessa, voitta- kametsä säilyy rakennuksena, katsoa pitkälle tulevaisuu- mine Suomen mestaruuksi- Tapparan perinteet erityi- misen taito Pekka Marjamä- päinvastoin kuin muutamalle teen ja tehdä päätöksiä, ny- neen 1970-luvun puolen välin sesti 2000-luvulla palaut- essä ja Janne Ojasessa. Ja jääkiekkopyhätölle on käynyt kytermein sanottuna, ”isosti”. jälkeen ja SM-liigan perusta- taneen Jukka Rautakorven niin monessa nyt mainitsemat- jääkiekkoilun emämaassa Ka- Yksi tällainen päätös teh- misen ensimmäisine play offs valmennuksessa Tappara ta jäävässä muussa Tapparan nadassa. tiin aikoinaan 1960-luvulla, -otteluineen. voitti pitkän odotuksen jäl- Hakametsän ajan menestystä Tapparalaiset kiittävät voi- kun kaupunki rohkeasti otti keen mestaruuden 2003. Sa- luomassa olleessa pelaajassa. dessaan tulla muistelemaan järjestääkseen jääkiekkoilun alevi ”Kallu” Nummi- moin teki Jussi ”Jupe” Ta- Olkaa ylpeitä. Olette teh- menneitä vanhaan Kotiimme MM-kisat vuonna 1965 ja ra- Knen pääsi nostamaan Ka- pola kausilla 2016 ja 2017, neet historiaa Hakametsässä. vielä senkin jälkeen, kun siir- kennutti Hakametsään pika- nada-maljaa vihdoin kohti Ha- joista ensimmäisen Hakamet- Tappara kiittää! rymme Areena-aikaan. Mutta vauhdilla silloisessa mittakaa- kametsänkin kattoa keväällä sässä, kuten me kaikki hyvin sitä ennen, me tapparalaiset vassa eurooppalaisittainkin 1977.