Last Name Analysis of Mobility, Gender Imbalance, and Nepotism Across Academic Systems Supporting Information
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

On Behalf of the Members and the Board of Directors of the Southern California Genealogical Society, Welcome to Today's Sessio
On behalf of the members and the Board of Directors of the Southern California Genealogical Society, welcome to today’s session! We hope that you enjoy it and that you’ll learn a new aspect of family history research from our speaker. Please spread the word about the Jamboree Extension Series. Tell your cousins and fellow genealogists. Upcoming presentations are listed at http://www.scgsgenealogy.com/JamboreeExtensionSeries2011.htm. Announcements of new sessions will be made through the SCGS blog at www.scgsgenealogy.blogspot.com. You can register to receive updates by email. Remember all these sessions are free and the original webcast is open to the public. All of the Jamboree Extension Series sessions will be archived and available for viewing 24/7 on the members-only portion of the SCGS website. This is only one of many benefits available for members of SCGS. You can join online at http://www.scgsgenealogy.com/catalog/index.php?cPath=30. Can you imagine what it would be among 1800 fellow genealogists and family historians, all of whom are enjoying informative sessions by knowledgeable and professional speakers? That’s the description of the Southern California Genealogy Jamboree, which will be held June 10-12, 2011, in Burbank. Keep updated on all things Jamboree by subscribing to email updates from the conference blog at www.genealogyjamboree.blogspot.com. If you have suggestions for improvement or ideas for future sessions, please contact us at [email protected]. Southern California Genealogical Society & Family Research Library Southern California Genealogy Jamboree 417 Irving Drive Burbank, CA 91504-2408 Office – 818.843.7247 • Fax – 818.688.3253 • [email protected] www.scgsgenealogy.com www.scgsgenealogy.blogspot.com www.genealogyjamboree.blogspot.com Tracing Your Immigrant Ancestors Presented by Lisa A. -

The Search for Lady Rose. Jeff Lewy Discusses the Mystery of His Titled Relative, Lady Rose, and How His Research Found the Answer
The Journal of the San Francisco Bay Area Jewish Genealogical Society Volume XXVIII, Number 2 May 2008 The Search for Lady Rose. Jeff Lewy discusses the mystery of his titled relative, Lady Rose, and how his research found the answer. See page 5. Also Inside this Issue SFBAJGS Counts Prominent Experts Among its Members....................................................3 All That Jazz, Genealogy Style.....................11 Departments Wedding of Basil Henriques and Rose Loewe, England, 1916. See page 7. Calendar.....................................................4, 12 President’s Message....................................... 2 Society News....................................................3 Family Finder Update.....................................10 Contributors to this Issue Jerry Delson, Beth Galleto, Jeremy Frankel, Excitement is building for the annual conference in Jeff Lewy. Chicago. See page 11. ZichronNote Journal of the San Francisco Bay Area Jewish Genealogical Society President’s Message ZichronNote Thoughts on Journal of the San Francisco Bay Area Jewish Genealogical Society Passover and Genealogy By Jeremy Frankel, SFBAJGS President © 2008 San Francisco Bay Area Jewish Genealogical Society I am writing this message at the time of year we celebrate Passover, when we recall the time our ZichronNote is published four times per year, in February, ancestors left the land of Mitzraim and spent 40 May, August and November. The deadline for contributions years wandering around the desert before entering is the first of the month preceding publication. The editor reserves the right to edit all submittals. Submissions may the Promised Land. Some people might view our be made by hard copy or electronically. Please email to passion for genealogy the same way; we take leave [email protected]. of our senses, spend many years lost in thought, and eventually (hopefully) we reach a satisfactory Reprinting of material in ZichronNote is hereby granted conclusion. -

Instructions to Conform Legal Name of an Adult
INSTRUCTIONS TO CONFORM LEGAL NAME OF AN ADULT A person desiring to file an Application to Conform Legal Name of an Adult must have been a bona fide resident of Hamilton County for at least 60 days immediately prior to the filing of said application. You must present a certified copy of the adult’s birth certificate at the time of the Application as well as proof and support documentation showing the name that the applicant has been using. The support documentation must include an Official Identity Document (e.g., Driver’s License, passport, social security card, Medicaid/Medicare Card, Military ID, certified copy of Marriage License, etc.). The conformed name must be one of the names used on at least one Official Identity Document. Fill in all blanks except Case No. and hearing dates. A fee is required at the time of filing. Current Court Costs are posted at: https://www.probatect.org/about/general-resources. This fee must be paid in cash, money order, certified check (made payable to PROBATE COURT), MasterCard, Discover, American Express, or Visa. No personal checks will be accepted. The forms may be obtained from the Information Desk on the 9th floor of the Probate Court, 230 East 9th Street, Cincinnati, Ohio or by downloading the forms from our Web site, http://www.probatect.org. STEP 1: COMPLETE THE FOLLOWING FORMS Application to Conform Legal Name of Adult (Form 121.00) - Be sure to state your full legal name (first, middle and last) and full name requested after the name is conformed (first, middle and last). -

FOI/EIR FOI Section/Regulation S.8 Issue Pseudonyms Line to Take
FOI/EIR FOI Section/Regulation s.8 Issue Pseudonyms Line to take: Section 8 states that a request for information should state the name of the applicant. This means the applicant’s real name. Therefore a request made by an applicant using a pseudonym is not valid and the public authori ty would not be obliged to deal with the request. Similarly the Commissioner is not obliged to deal with a complaint made using a pseudonym as technically he has no legal authority to consider such complaints. However, it is the Commissioner’s position th at it would be contrary to the spirit of the Act to routinely or randomly check a complainant’s identity. Therefore the Commissioner will only decline to issue decision notices where the name used by the applicant is an obvious pseudonym or it comes to lig ht during the course of an investigation that the request was made using a pseudonym. Where the applicant has used what seems to be an obvious pseudonym, the onus is on the applicant to prove that they are in fact known by that name and thus that they have made a valid request. Where the requestor has used a name other than an obvious pseudonym, the Commissioner will assume that the applicant has provided his/her real name and expects public authorities to do likewise. If however a public authority suspect s the name given is false and refuses to deal with the request on that basis, it will then be up to the public authority to provide evidence to show that they have good reason to believe that the name used is a pseudonym and thus is an invalid request. -

Data Standards Document
GEORGE MASON UNIVERSITY DATA STANDARDS DOCUMENT GGeeoorrggee MMaassoonn UUnniivveerrssiittyy PPaattrriioott PPrroojjeecctt DDaattaa SSttaannddaarrddss DDooccuummeenntt Last Updated: August 19, 2013 1 GEORGE MASON UNIVERSITY DATA STANDARDS DOCUMENT Table of Contents Chapter 1: Policies and Definitions ................................................................................... 4 Data Standards Development and Maintenance ........................................................................ 4 Current Committee Mission .................................................................................................... 4 Current Committee/Consultant Representation ...................................................................... 4 Committee Assignment .......................................................................................................... 5 Rules and Procedures ............................................................................................................ 5 Person Role Definitions and Assignments .................................................................................. 5 General Person Initial Entry and/or Update Responsibilities Role ................................................. 7 Chapter 2: Data Standards ................................................................................................... 8 Identification Number Standards ................................................................................................. 8 Name Standards ........................................................................................................................ -

Change of Name of an Adult
INSTRUCTIONS FOR CHANGE OF NAME OF AN ADULT A person desiring to file an Application for Change of Name of an Adult must have been a bona fide resident of Hamilton County for at least 60 days immediately prior to the filing of said application. Fill in all blanks except Case No. and hearing dates. A fee is required at the time of filing. Current Court Costs are posted at: https://www.probatect.org/about/general-resources. This fee must be paid in cash, money order, certified check (made payable to PROBATE COURT), MasterCard, Discover, American Express, or Visa. No personal checks will be accepted. IMPORTANT INFORMATION ABOUT PUBLICATION: Beginning August 17, 2021, Ohio Law no longer requires that applications to Change Name be set for formal hearing. However, a hearing may still be required in the Court’s discretion. If a hearing is requested by the Court, the application will be set for hearing at a future date and publication of notice may be required in a newspaper of general circulation in the County at least thirty (30) days before the hearing on the application. Otherwise, the application will be considered by the Magistrate who reviews the documents. If publication is required, you will use the NOTICE OF HEARING ON CHANGE OF NAME for this purpose. If you use the Cincinnati Court Index Press the NOTICE OF HEARING ON CHANGE OF NAME will be left with the cashier and the Cincinnati Court Index Press will pick up the notice. The Cincinnati Court Index Press will be paid directly by the Court from the initial filing fees for this case. -

Marketing “Proper” Names: Female Authors, Sensation
MARKETING “PROPER” NAMES: FEMALE AUTHORS, SENSATION DISCOURSE, AND THE MID-VICTORIAN LITERARY PROFESSION By Heather Freeman Dissertation Submitted to the Faculty of the Graduate School of Vanderbilt University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY in English August, 2013 Nashville, Tennessee Approved: Carolyn Dever Jay Clayton Rachel Teukolsky James Epstein Copyright © 2013 by Heather Freeman All Rights Reserved For Sean, with gratitude for your love and unrelenting support iii ACKNOWLEDGEMENTS This dissertation would not have been possible without the influence, patience, and feedback of a number of people, but I owe a particular debt to my committee, Professors Carolyn Dever, Jay Clayton, Rachel Teukolsky, and Jim Epstein. Their insightful questions and comments not only strengthened this project but also influenced my development as a writer and a critic over the last five years. As scholars and teachers, they taught me how to be engaged and passionate in the archive and in the classroom as well. My debt to Carolyn Dever, who graciously acted as my Director, is, if anything, compound. I cannot fully express my gratitude for her warmth, patience, incisive criticism, and unceasing willingness to read drafts, even when she didn’t really have the time. The administrative women of the English Department provided extraordinary but crucial support and encouragement throughout my career at Vanderbilt. Particular thanks go to Janis May and Sara Corbitt, and to Donna Caplan, who has provided a friendly advice, a listening ear, and much-needed perspective since the beginning. I also owe a great deal of thanks to my colleagues in the graduate program at Vanderbilt. -
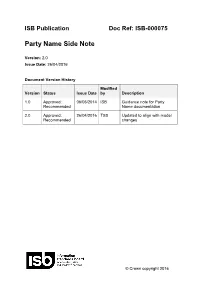
Party Name Side Note
ISB Publication Doc Ref: ISB-000075 Party Name Side Note Version: 2.0 Issue Date: 26/04/2016 Document Version History Modified Version Status Issue Date by Description 1.0 Approved: 06/05/2014 ISB Guidance note for Party Recommended Name documentation 2.0 Approved: 26/04/2016 TSS Updated to align with model Recommended changes © Crown copyright 2016 Party Name Side Note Contents 1 Introduction ________________________________________________ 4 1.1 Purpose ______________________________________________________ 4 1.2 Scope ________________________________________________________ 5 1.3 Business Data Architecture (BDA) Model Version ______________________ 5 2 Design Concept _____________________________________________ 6 2.1 Business Requirements __________________________________________ 6 2.1.1 (Party of type) Person ________________________________________________ 6 2.1.2 (Party of type) Organisation ___________________________________________ 7 2.1.3 Common (to both person and organisation types of Party) ___________________ 7 2.2 Entity Definition Models __________________________________________ 8 2.3 Attribute Models ________________________________________________ 9 3 How the Structure resolves the Business Requirements __________ 10 3.1 Multiple names ________________________________________________ 10 3.2 Re-usable name bank __________________________________________ 11 3.3 Parsing a name _______________________________________________ 12 3.4 Name components ordering ______________________________________ 13 3.5 Single design for -

Best Practice Recommendations for the Collection of Key Patient Data Attributes
Best Practice Recommendations for the Collection of Key Patient Data Attributes Prepared by the National Association of Healthcare Access Management October 2016 Introduction The National Association of Health Access Management (NAHAM) has developed these Best Practice Recommendations for the Collection of Key Patient Data Attributes in coordination with the work on patient matching by the Office of the National Coordinator for Health Information Technology (ONC), which has most recently identified the following patient data attributes as the 2015 criteria for Certified EHR Technology (CEHRT):1 First name Last name Previous name Middle name (including middle initial) Suffix Date of birth Address Phone number Sex NAHAM has reorganized these attributes into the five Best Practice Recommendations presented below:2 1. Patient name 2. Date of birth 3. Address 4. Phone number 5. Sex and gender 1 These attributes are also identified and discussed in the ONC’s 2014 Patient Identification and Matching Final Report (“2014 Final Report”). 2 NAHAM recognizes that each organization will have developed its own, perhaps unique, patient inquiry protocols and uses secondary identifiers only if certain primary identifiers fail to produce a patient match. For example, an organization may use name, date of birth, and social security number as primary search criteria. If these fail to produce a match, the organization may use sex, address, and phone number as secondary criteria. Organizations may also choose to use other demographic data that are considered reliable and not subject to change as patient identifiers. © 2016 National Association of Healthcare Access Management (NAHAM) Introduction 1 Patient name includes separate fields for first name, last name, previous name, middle name or initial, and suffix. -

Employment Application
**$100 SIGN ON BONUS! WORK 50 HOURS WITHIN 3 MONTHS OF HIRE DATE, RECEIVE $100** Dear Applicant, Thank you for your interest in Respite Connection. Enclosed you will find the 2-page application and job descriptions, as well as the “Non-Law Enforcement Record Check Request” form to allow us to complete criminal background checks. Please fill out the information in the middle of the “Non-Law Enforcement Record Check Request” and sign at the bottom. You need to add each last name you have had as an adult on the form (that includes maiden and married names). If you have only had one last name, only fill the last name blank. We are required to run child and dependent adult abuse background checks as well, but those do not require your signature (just the permission you grant when you sign the application). Complete and return the application and the “Non-Law Enforcement Record Check Request” form to the address below. You may include a resume in addition to the application, but that is not required. Thanks for your interest in caring for children and adults with special needs! Sincerely, Missy Ringgenberg, Director Abbie Jones, Human Resource Coordinator 2469 106th Street, Urbandale, IA 50322 Phone: 515.277.1050, Fax: 515.277.1963 2469 106th Street, Urbandale, IA 50322 Phone: 515.277.1050, Fax: 515.277.1963 APPLICATION Today’s Date: Full Name: First Last MI Address: Street Address City State Zip County: Social Security #: Home Phone: Cell Phone: Email Address: Work Phone: What is the best way to reach you? Home Phone Cell Phone Work Phone Email -

The Grown-Up Genealogist
The grown-up genealogist Volume 23 Issue 11 By Pamela Erickson (www.FamilyScribe.us) November 2012 I recently saw a sign that got me thinking about the behavior of our toddler grandsons and the adult stu- dents in my genealogy classes. They can’t be more different. Here are the anonymous Toddlers’ Rules of Possessions from the sign: 1. If I like it, it’s mine. 2. If it’s in my hand, it’s mine. 3. If I can take it from you, it’s mine. 4. If I had it a little while ago, it’s mine. 5. If it’s mine, it must NEVER appear to be yours in any way. 6. If I’m doing or building something, all the pieces are mine. 7. If it looks just like mine, it is mine. 8. If I saw it first, it’s mine. 9. If you are playing with something and put it down, it automatically becomes mine. 10. If it’s broken, it’s yours. ER GENEALOGY GROUP While I appreciate the humor of the ten rules above, I know that with maturity, the acceptance of these rules is unreason- able for adults. How many times have I looked for supporting information for a particular ancestor with no success and set it aside for an- other day? When I pick up the search again and look online, I often find someone else has already found what I was looking for and put it in their supporting data for all to see. Or, in an- other example, after a period of time I don’t always remember (Continued on page 2) SILICON VALLEY COMPUT Outside and inside Genealogist’s Rules of Possession, How I found it, page 6 PastFinder above Upcoming meetings, page 8 Finding marriage records, page 3 About the group, page 8 The grown-up genealogist (Continued from page 1) whether I created the original or copied ship of how the material is con- veyed, particularly if it's narrative. -

Searching for Female Ancestors: a Selected Bibliography
SEARCHING FOR FEMALE ANCESTORS: A SELECTED BIBLIOGRAPHY The focus of this bibliography is genealogy, not women’s history. Therefore, general guides and women’s history resources are included only when they make possible the identification of individuals and families, or when they help elucidate repositories or search strategies that can help the family historian seeking female ancestors. An assumption has been made that most researchers would like broader information about the lives and life circumstances. In other words, moving beyond birth, marriage, and death dates if this data is sufficiently concrete and focused on the ancestor’s specific case. For sources with a geographical focus (county, state, and regional sources), a title is included when consulting it may lead the family historian to discover categories of useful primary source materials, or when the title appears to be a unique source worthy of notice. At the county level, increasing amounts of material useful in tracing women, such as marriage license indexes and court records, are becoming available online. For the most part it is impractical to list these web sites because changes in them occur so frequently. Where sources focus on men, or include men and women together, one assumes that they will be discovered in routine genealogical research and, in general, are not included below. Indexes to vital records, especially marriage records, normally include a list of both males and females; and therefore such indexes are listed here only when, for whatever reason, a separate index for women was published. Exceptions to this rule are bibliographies of diaries, both published and unpublished.