Oracle® Developer Studio 12.6: Performance Library User's Guide
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Fortran Resources 1
Fortran Resources 1 Ian D Chivers Jane Sleightholme May 7, 2021 1The original basis for this document was Mike Metcalf’s Fortran Information File. The next input came from people on comp-fortran-90. Details of how to subscribe or browse this list can be found in this document. If you have any corrections, additions, suggestions etc to make please contact us and we will endeavor to include your comments in later versions. Thanks to all the people who have contributed. Revision history The most recent version can be found at https://www.fortranplus.co.uk/fortran-information/ and the files section of the comp-fortran-90 list. https://www.jiscmail.ac.uk/cgi-bin/webadmin?A0=comp-fortran-90 • May 2021. Major update to the Intel entry. Also changes to the editors and IDE section, the graphics section, and the parallel programming section. • October 2020. Added an entry for Nvidia to the compiler section. Nvidia has integrated the PGI compiler suite into their NVIDIA HPC SDK product. Nvidia are also contributing to the LLVM Flang project. Updated the ’Additional Compiler Information’ entry in the compiler section. The Polyhedron benchmarks discuss automatic parallelisation. The fortranplus entry covers the diagnostic capability of the Cray, gfortran, Intel, Nag, Oracle and Nvidia compilers. Updated one entry and removed three others from the software tools section. Added ’Fortran Discourse’ to the e-lists section. We have also made changes to the Latex style sheet. • September 2020. Added a computer arithmetic and IEEE formats section. • June 2020. Updated the compiler entry with details of standard conformance. -

Oracle® Developer Studio 12.6
® Oracle Developer Studio 12.6: C++ User's Guide Part No: E77789 July 2017 Oracle Developer Studio 12.6: C++ User's Guide Part No: E77789 Copyright © 2017, Oracle and/or its affiliates. All rights reserved. This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, delivered to U.S. Government end users are "commercial computer software" pursuant to the applicable Federal Acquisition Regulation and agency-specific supplemental regulations. As such, use, duplication, disclosure, modification, and adaptation of the programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, shall be subject to license terms and license restrictions applicable to the programs. -

Sicstus Prolog Release Notes Mats Carlsson Et Al
SICStus Prolog Release Notes Mats Carlsson et al. RISE Research Institutes of Sweden AB PO Box 1263 SE-164 29 Kista, Sweden Release 4.7.0 July 2021 RISE Research Institutes of Sweden AB [email protected] https://sicstus.sics.se/ Copyright c 1995-2021 RISE Research Institutes of Sweden AB RISE Research Institutes of Sweden AB PO Box 1263 SE-164 29 Kista, Sweden Permission is granted to make and distribute verbatim copies of these notes provided the copyright notice and this permission notice are preserved on all copies. Permission is granted to copy and distribute modified versions of these notes under the con- ditions for verbatim copying, provided that the entire resulting derived work is distributed under the terms of a permission notice identical to this one. Permission is granted to copy and distribute translations of these notes into another lan- guage, under the above conditions for modified versions, except that this permission notice may be stated in a translation approved by SICS. i Table of Contents 1 Overview ::::::::::::::::::::::::::::::::::::::::: 1 2 Platforms :::::::::::::::::::::::::::::::::::::::: 2 3 Release Notes and Installation Guide for UNIX :: 3 3.1 Installation ::::::::::::::::::::::::::::::::::::::::::::::::::::: 3 3.1.1 Prerequisites::::::::::::::::::::::::::::::::::::::::::::::: 3 3.1.1.1 C Compiler and Linker:::::::::::::::::::::::::::::::: 3 3.1.2 The Installation Script ::::::::::::::::::::::::::::::::::::: 3 3.1.3 The Uninstallation Script :::::::::::::::::::::::::::::::::: 4 3.2 Platform Specific Notes -
Fortran Free Ide
Fortran free ide click here to download Code::Blocks is a free, cross platform Integrated Development Environment (IDE) (www.doorway.ru). This site is for those, who would like to use. Free personal www.doorway.ru Welcome to the home of Silverfrost FTN Fortran for Windows (formally Salford FTN95). editor the way nature intended; Included - Use FTN95 with the powerful Plato IDE -- included with all versions of FTN Depends on the machine you are using. In Intel Fortran environment you have available automatic optimization which is usually much better than in gfortran. I am using GNU gfortran, but I am not always satisfied with compilation. The only fortran compiler . What is the best and most comfortable free Fortran IDE?. Code::Blocks is a free C, C++ and Fortran IDE built to meet the most demanding needs of its users. It is designed to be very extensible and fully configurable. Free compilers and interpreters for the Fortran programming Free Fortran Compilers and Integrated Development Environments (IDEs). The latest version of the Fortran Tools includes gfortran and the latest version of Code::Blocks, as well as updates of much of the included software and. The AbsoftTools Fortran IDE provides a complete solution for Fortran programming Programmer's editor, compiler, debugger, application framework, math and. Code::Blocks IDE for Fortran An IDE for Fortran and editor that supports fixed-format Fortran 77 and free-format Fortran IDE- FORTRAN package. macOS Build Status Dependency Status Package version Plugin installs. Fortran language support for Atom-IDE, powered by the. Photran is an IDE and refactoring tool for Fortran based on Eclipse and the CDT. -
Optimization in Code Generationto Reduce Energy
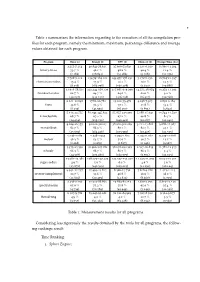
1 Table 1 summarizes the information regarding to the execution of all the compilation pro- files for each program, namely the minimum, maximum, percentage difference and average values obtained for each program. Program Time (s) Energy (J) CPU (J) Memory (J) Energy/Time (J/s) 3.355-7.214 40.843-78.631 37.606-72.630 3.231-6.029 10.860-12.264 binary-trees 53.5 % 48.1 % 48.2 % 46.4 % 11.4 % (5.186) (58.844) (54.286) (4.558) (11.576) 7.706-9.112 154.74-184.101 149.475-178.231 5.172-6.156 18.724-21.397 chameneos-redux 15.4 % 15.9 % 16.1 % 16.0 % 12.5 % (8.358) (166.098) (160.478) (5.620) (19.888) 21.918-58.501 232.244-658.129 217.685-619.299 14.553-38.874 10.273-11.293 fannkuch-redux 62.5 % 64.7 % 64.8 % 62.6 % 9.0 % (40.537) (443.155) (416.238) (26.917) (10.768) 6.101-10.848 17.86-66.781 13.612-59.476 4.248-7.305 2.892-6.184 fasta 43.8 % 73.3 % 77.1 % 41.8 % 53.2 % (8.439) (41.991) (36.190) (5.801) (4.622) 7.113-22.755 81.043-245.822 75.857-230.399 5.186-15.641 10.744-11.730 k-nucleotide 68.7 % 67.0 % 67.1 % 66.8 % 8.4 % (14.434) (159.531) (149.443) (10.087) (11.241) 4.624-26.755 42.022-320.07 38.910-302.269 3.111-17.806 9.086-11.967 mandelbrot 82.7 % 86.9 % 87.1 % 82.5 % 24.1 % (15.639) (184.416) (173.991) (10.425) (11.525) 0.046-0.089 0.425-0.934 0.393-0.874 0.032-0.060 9.239-10.678 meteor 48.3 % 54.5 % 55.0 % 46.7 % 13.5 % (0.068) (0.683) (0.637) (0.046) (9.967) 3.473-25.390 40.966-307.182 38.658-290.323 2.307-16.859 11.781-12.455 n-body 86.3 % 86.7 % 86.7 % 86.3 % 5.4 % (14.308) (172.280) (162.779) (9.501) (12.103) 13.781-14.485 138.577-147.229 -

License Information User Manual Oracle® Developer Studio 12.6
® License Information User Manual Oracle Developer Studio 12.6 Last Updated: JUNE 2017 Part No: E77805 June 2017 License Information User Manual Oracle Developer Studio 12.6 Part No: E77805 Copyright © 2015, 2017, Oracle and/or its affiliates. All rights reserved. This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, delivered to U.S. Government end users are "commercial computer software" pursuant to the applicable Federal Acquisition Regulation and agency-specific supplemental regulations. As such, use, duplication, disclosure, modification, and adaptation of the programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, shall be subject to license terms and license restrictions applicable to the programs. -

Using Oracle Developer Cloud Service Traditional
Oracle® Cloud Using Oracle Developer Cloud Service Traditional E92763-07 August 2019 Oracle Cloud Using Oracle Developer Cloud Service Traditional, E92763-07 Copyright © 2014, 2019, Oracle and/or its affiliates. All rights reserved. Primary Author: Himanshu Marathe Contributing Authors: Eric Jendrock Contributors: Oracle Developer Cloud Service development team This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, delivered to U.S. Government end users are "commercial computer software" pursuant to the applicable Federal Acquisition Regulation and agency- specific supplemental regulations. As such, use, duplication, disclosure, modification, and adaptation of the programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, shall be subject to license terms and license restrictions applicable to the programs. -

Oracle® Developer Studio 12.5: Release Notes
® Oracle Developer Studio 12.5: Release Notes Part No: E60741 May 2017 Oracle Developer Studio 12.5: Release Notes Part No: E60741 Copyright © 2016, 2017, Oracle and/or its affiliates. All rights reserved. This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, delivered to U.S. Government end users are "commercial computer software" pursuant to the applicable Federal Acquisition Regulation and agency-specific supplemental regulations. As such, use, duplication, disclosure, modification, and adaptation of the programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, shall be subject to license terms and license restrictions applicable to the programs. No other rights are granted to the U.S. -

Sourcepro® 2016.2 Supported Platforms
Legend MicrosoftWindows2016 Server MicrosoftWindows2012 R2 Server MicrosoftWindows2012 Server MicrosoftWindows 10 MicrosoftWindows 8.1 R2Microsoft Windows2008 Server MicrosoftWindows 7 Windows Solaris Oracle 11 Solaris Oracle 10 Solaris Linux 7 Oracle 7 CentOS 7 Linux Enterprise Hat Red 6 CentOS 6 Linux Enterprise Hat Red 5 CentOS 5 Linux Enterprise Hat Red SuSELinux 12 Enterprise Server SuSELinux 11 Enterprise Server Linux v3 11i HP-UX HP HP-UX AIX7.2 IBM AIX6.1 IBM AIX OS bold A - - - 64-bittarget binaries only since last New release SupportedPlatform Supported Platforms SourcePro Intel C++ 2016 C++ Intel Studio (2012, Visual 2013,Microsoft 2015, 2016 C++ Intel Studio (2012, Visual 2013,Microsoft 2015, 2016 C++ Intel Studio (2012, Visual 2013,Microsoft 2015, 2016 C++ Intel Studio (2012, Visual 2013,Microsoft 2015, 2016 C++ Intel Studio (2012, Visual 2013,Microsoft 2015, 2016 C++ Intel Studio (2012, Visual 2013,Microsoft 2015, 2016 C++ Intel Studio (2012, Visual 2013,Microsoft 2015, StudioDeveloper Oracle 12.5 Solaris Oracle Studio 12.4 StudioDeveloper Oracle 12.5 Solaris Oracle Studio 12.4 OracleDeveloper Studio 12.5 IntelC++ 2016 GCC 4.8 GNU IntelC++ 2016 GCC 4.4 GNU IntelC++ 2016 GCC 4.1 GNU GCC 4.8 GNU GCC 4.3 GNU A.06.28 aCC HP C++ IBM13.1 XL C++ IBM13.1 XL Compiler ® (with Visual Studio 2015)Studio (with Visual 2015)Studio (with Visual 2015)Studio (with Visual 2015)Studio (with Visual 2015)Studio (with Visual 2015)Studio (with Visual 2015)Studio (with Visual 2016.2 2017 2017 2017 2017 2017 2017 2017 ) ) ) ) ) ) ) x86-64 x86-64 -

Oracle® Developer Studio 12.6: IDE Quick Start Tutorial
® Oracle Developer Studio 12.6: IDE Quick Start Tutorial Part No: E77787 June 2017 Oracle Developer Studio 12.6: IDE Quick Start Tutorial Part No: E77787 Copyright © 2013, 2017, Oracle and/or its affiliates. All rights reserved. This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, delivered to U.S. Government end users are "commercial computer software" pursuant to the applicable Federal Acquisition Regulation and agency-specific supplemental regulations. As such, use, duplication, disclosure, modification, and adaptation of the programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, shall be subject to license terms and license restrictions applicable to the programs. -

Using Oracle Developer Cloud Service
Oracle® Cloud Using Oracle Developer Cloud Service E37145-38 October 2019 Oracle Cloud Using Oracle Developer Cloud Service, E37145-38 Copyright © 2014, 2019, Oracle and/or its affiliates. All rights reserved. Primary Author: Himanshu Marathe Contributing Authors: Eric Jendrock Contributors: Oracle Developer Cloud Service development team This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, delivered to U.S. Government end users are "commercial computer software" pursuant to the applicable Federal Acquisition Regulation and agency- specific supplemental regulations. As such, use, duplication, disclosure, modification, and adaptation of the programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, shall be subject to license terms and license restrictions applicable to the programs. -

Oracle® Developer Studio 12.6
® Oracle Developer Studio 12.6: Overview Part No: E77786 February 2018 Oracle Developer Studio 12.6: Overview Part No: E77786 Copyright © 2011, 2018, Oracle and/or its affiliates. All rights reserved. This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, delivered to U.S. Government end users are "commercial computer software" pursuant to the applicable Federal Acquisition Regulation and agency-specific supplemental regulations. As such, use, duplication, disclosure, modification, and adaptation of the programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, shall be subject to license terms and license restrictions applicable to the programs. No other rights are granted to the U.S.