Ages of Young Stars
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
![Arxiv:2012.09981V1 [Astro-Ph.SR] 17 Dec 2020 2 O](https://docslib.b-cdn.net/cover/3257/arxiv-2012-09981v1-astro-ph-sr-17-dec-2020-2-o-73257.webp)
Arxiv:2012.09981V1 [Astro-Ph.SR] 17 Dec 2020 2 O
Contrib. Astron. Obs. Skalnat´ePleso XX, 1 { 20, (2020) DOI: to be assigned later Flare stars in nearby Galactic open clusters based on TESS data Olga Maryeva1;2, Kamil Bicz3, Caiyun Xia4, Martina Baratella5, Patrik Cechvalaˇ 6 and Krisztian Vida7 1 Astronomical Institute of the Czech Academy of Sciences 251 65 Ondˇrejov,The Czech Republic(E-mail: [email protected]) 2 Lomonosov Moscow State University, Sternberg Astronomical Institute, Universitetsky pr. 13, 119234, Moscow, Russia 3 Astronomical Institute, University of Wroc law, Kopernika 11, 51-622 Wroc law, Poland 4 Department of Theoretical Physics and Astrophysics, Faculty of Science, Masaryk University, Kotl´aˇrsk´a2, 611 37 Brno, Czech Republic 5 Dipartimento di Fisica e Astronomia Galileo Galilei, Vicolo Osservatorio 3, 35122, Padova, Italy, (E-mail: [email protected]) 6 Department of Astronomy, Physics of the Earth and Meteorology, Faculty of Mathematics, Physics and Informatics, Comenius University in Bratislava, Mlynsk´adolina F-2, 842 48 Bratislava, Slovakia 7 Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, H-1121 Budapest, Konkoly Thege Mikl´os´ut15-17, Hungary Received: September ??, 2020; Accepted: ????????? ??, 2020 Abstract. The study is devoted to search for flare stars among confirmed members of Galactic open clusters using high-cadence photometry from TESS mission. We analyzed 957 high-cadence light curves of members from 136 open clusters. As a result, 56 flare stars were found, among them 8 hot B-A type ob- jects. Of all flares, 63 % were detected in sample of cool stars (Teff < 5000 K), and 29 % { in stars of spectral type G, while 23 % in K-type stars and ap- proximately 34% of all detected flares are in M-type stars. -

Young Nearby Stars by Adam Conrad Schneider (Under The
Young Nearby Stars by Adam Conrad Schneider (Under the Direction of Professor Inseok Song) Abstract Nearby young stars are without equal as stellar and planetary evolution laboratories. The aim of this work is to use age diagnostic considerations to execute a complete survey for new nearby young stars and to efficiently reevaluate and constrain their ages. Because of their proximity and age, young, nearby stars are the most desired targets for any astrophysical study focusing on the early stages of star and planet formation. Identifying nearby, young, low-mass stars is challenging because of their inherent faint- ness and age diagnostic degeneracies. A new method for identifying these objects has been developed, and a pilot study of its effectiveness is demonstrated by the identification of two definite new members of the TW Hydrae Association. Nearby, young, solar-type stars are initially identified in this work by their fractional X-ray luminosity. The results of a large-scale search for nearby, young, solar-type stars is presented. Follow-up spectroscopic observations are taken in order to measure various age diagnostics in order to accurately assess stellar ages. Age, one of the most fundamental properties of a star, is also one of the most difficult to determine. While a variety of proce- dures have been developed and utilized to approximate ages for solar-type stars, with varying degrees of success, a comprehensive age-dating technique has yet to be constructed. Often- times, different methods exhibit contradictory or conflicting findings. Such inconsistencies demonstrate the value of a uniform method of determining stellar ages. -

Curriculum Vitae - 24 March 2020
Dr. Eric E. Mamajek Curriculum Vitae - 24 March 2020 Jet Propulsion Laboratory Phone: (818) 354-2153 4800 Oak Grove Drive FAX: (818) 393-4950 MS 321-162 [email protected] Pasadena, CA 91109-8099 https://science.jpl.nasa.gov/people/Mamajek/ Positions 2020- Discipline Program Manager - Exoplanets, Astro. & Physics Directorate, JPL/Caltech 2016- Deputy Program Chief Scientist, NASA Exoplanet Exploration Program, JPL/Caltech 2017- Professor of Physics & Astronomy (Research), University of Rochester 2016-2017 Visiting Professor, Physics & Astronomy, University of Rochester 2016 Professor, Physics & Astronomy, University of Rochester 2013-2016 Associate Professor, Physics & Astronomy, University of Rochester 2011-2012 Associate Astronomer, NOAO, Cerro Tololo Inter-American Observatory 2008-2013 Assistant Professor, Physics & Astronomy, University of Rochester (on leave 2011-2012) 2004-2008 Clay Postdoctoral Fellow, Harvard-Smithsonian Center for Astrophysics 2000-2004 Graduate Research Assistant, University of Arizona, Astronomy 1999-2000 Graduate Teaching Assistant, University of Arizona, Astronomy 1998-1999 J. William Fulbright Fellow, Australia, ADFA/UNSW School of Physics Languages English (native), Spanish (advanced) Education 2004 Ph.D. The University of Arizona, Astronomy 2001 M.S. The University of Arizona, Astronomy 2000 M.Sc. The University of New South Wales, ADFA, Physics 1998 B.S. The Pennsylvania State University, Astronomy & Astrophysics, Physics 1993 H.S. Bethel Park High School Research Interests Formation and Evolution -

Winter Constellations
Winter Constellations *Orion *Canis Major *Monoceros *Canis Minor *Gemini *Auriga *Taurus *Eradinus *Lepus *Monoceros *Cancer *Lynx *Ursa Major *Ursa Minor *Draco *Camelopardalis *Cassiopeia *Cepheus *Andromeda *Perseus *Lacerta *Pegasus *Triangulum *Aries *Pisces *Cetus *Leo (rising) *Hydra (rising) *Canes Venatici (rising) Orion--Myth: Orion, the great hunter. In one myth, Orion boasted he would kill all the wild animals on the earth. But, the earth goddess Gaia, who was the protector of all animals, produced a gigantic scorpion, whose body was so heavily encased that Orion was unable to pierce through the armour, and was himself stung to death. His companion Artemis was greatly saddened and arranged for Orion to be immortalised among the stars. Scorpius, the scorpion, was placed on the opposite side of the sky so that Orion would never be hurt by it again. To this day, Orion is never seen in the sky at the same time as Scorpius. DSO’s ● ***M42 “Orion Nebula” (Neb) with Trapezium A stellar nursery where new stars are being born, perhaps a thousand stars. These are immense clouds of interstellar gas and dust collapse inward to form stars, mainly of ionized hydrogen which gives off the red glow so dominant, and also ionized greenish oxygen gas. The youngest stars may be less than 300,000 years old, even as young as 10,000 years old (compared to the Sun, 4.6 billion years old). 1300 ly. 1 ● *M43--(Neb) “De Marin’s Nebula” The star-forming “comma-shaped” region connected to the Orion Nebula. ● *M78--(Neb) Hard to see. A star-forming region connected to the Orion Nebula. -

February 14, 2015 7:00Pm at the Herrett Center for Arts & Science Colleagues, College of Southern Idaho
Snake River Skies The Newsletter of the Magic Valley Astronomical Society www.mvastro.org Membership Meeting President’s Message Saturday, February 14, 2015 7:00pm at the Herrett Center for Arts & Science Colleagues, College of Southern Idaho. Public Star Party Follows at the It’s that time of year when obstacles appear in the sky. In particular, this year is Centennial Obs. loaded with fog. It got in the way of letting us see the dance of the Jovian moons late last month, and it’s hindered our views of other unique shows. Still, members Club Officers reported finding enough of a clear sky to let us see Comet Lovejoy, and some great photos by members are popping up on the Facebook page. Robert Mayer, President This month, however, is a great opportunity to see the benefit of something [email protected] getting in the way. Our own Chris Anderson of the Herrett Center has been using 208-312-1203 the Centennial Observatory’s scope to do work on occultation’s, particularly with asteroids. This month’s MVAS meeting on Feb. 14th will give him the stage to Terry Wofford, Vice President show us just how this all works. [email protected] The following weekend may also be the time the weather allows us to resume 208-308-1821 MVAS-only star parties. Feb. 21 is a great window for a possible star party; we’ll announce the location if the weather permits. However, if we don’t get that Gary Leavitt, Secretary window, we’ll fall back on what has become a MVAS tradition: Planetarium night [email protected] at the Herrett Center. -
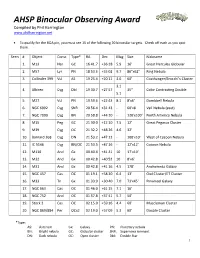
Binocular Challenge Here
AHSP Binocular Observing Award Compiled by Phil Harrington www.philharrington.net • To qualify for the BOA pin, you must see 15 of the following 20 binocular targets. Check off each as you spot them. Seen # Object Const. Type* RA Dec Mag Size Nickname 1. M13 Her GC 16 41.7 +36 28 5.9 16' Great Hercules Globular 2. M57 Lyr PN 18 53.6 +33 02 9.7 86"x62" Ring Nebula 3. Collinder 399 Vul AS 19 25.4 +20 11 3.6 60' Coathanger/Brocchi’s Cluster 3.1 4. Albireo Cyg Dbl 19 30.7 +27 57 35” Color Contrasting Double 5.1 5. M27 Vul PN 19 59.6 +22 43 8.1 8’x6’ Dumbbell Nebula 6. NGC 6992 Cyg SNR 20 56.4 +31 43 - 60'x8 Veil Nebula (east) 7. NGC 7000 Cyg BN 20 58.8 +44 20 - 120'x100' North America Nebula 8. M15 Peg GC 21 30.0 +12 10 7.5 12’ Great Pegasus Cluster 9. M39 Cyg OC 21 32.2 +48 26 4.6 32' 10. Barnard 168 Cyg DN 21 53.2 +47 12 - 100'x10' West of Cocoon Nebula 11. IC 5146 Cyg BN/OC 21 53.5 +47 16 - 12'x12' Cocoon Nebula 12. M110 And Gx 00 40.4 +41 41 10 17’x10’ 13. M32 And Gx 00 42.8 +40 52 10 8’x6’ 14. M31 And Gx 00 42.8 +41 16 4.5 178’ Andromeda Galaxy 15. NGC 457 Cas OC 01 19.1 +58 20 6.4 13’ Owl Cluster/ET Cluster 16. -

A Basic Requirement for Studying the Heavens Is Determining Where In
Abasic requirement for studying the heavens is determining where in the sky things are. To specify sky positions, astronomers have developed several coordinate systems. Each uses a coordinate grid projected on to the celestial sphere, in analogy to the geographic coordinate system used on the surface of the Earth. The coordinate systems differ only in their choice of the fundamental plane, which divides the sky into two equal hemispheres along a great circle (the fundamental plane of the geographic system is the Earth's equator) . Each coordinate system is named for its choice of fundamental plane. The equatorial coordinate system is probably the most widely used celestial coordinate system. It is also the one most closely related to the geographic coordinate system, because they use the same fun damental plane and the same poles. The projection of the Earth's equator onto the celestial sphere is called the celestial equator. Similarly, projecting the geographic poles on to the celest ial sphere defines the north and south celestial poles. However, there is an important difference between the equatorial and geographic coordinate systems: the geographic system is fixed to the Earth; it rotates as the Earth does . The equatorial system is fixed to the stars, so it appears to rotate across the sky with the stars, but of course it's really the Earth rotating under the fixed sky. The latitudinal (latitude-like) angle of the equatorial system is called declination (Dec for short) . It measures the angle of an object above or below the celestial equator. The longitud inal angle is called the right ascension (RA for short). -

Instruction Manual Meade Instruments Corporation
Instruction Manual 7" LX200 Maksutov-Cassegrain Telescope 8", 10", and 12" LX200 Schmidt-Cassegrain Telescopes Meade Instruments Corporation NOTE: Instructions for the use of optional accessories are not included in this manual. For details in this regard, see the Meade General Catalog. (2) (1) (1) (2) Ray (2) 1/2° Ray (1) 8.218" (2) 8.016" (1) 8.0" Secondary 8.0" Mirror Focal Plane Secondary Primary Baffle Tube Baffle Field Stops Correcting Primary Mirror Plate The Meade Schmidt-Cassegrain Optical System (Diagram not to scale) In the Schmidt-Cassegrain design of the Meade 8", 10", and 12" models, light enters from the right, passes through a thin lens with 2-sided aspheric correction (“correcting plate”), proceeds to a spherical primary mirror, and then to a convex aspheric secondary mirror. The convex secondary mirror multiplies the effective focal length of the primary mirror and results in a focus at the focal plane, with light passing through a central perforation in the primary mirror. The 8", 10", and 12" models include oversize 8.25", 10.375" and 12.375" primary mirrors, respectively, yielding fully illuminated fields- of-view significantly wider than is possible with standard-size primary mirrors. Note that light ray (2) in the figure would be lost entirely, except for the oversize primary. It is this phenomenon which results in Meade 8", 10", and 12" Schmidt-Cassegrains having off-axis field illuminations 10% greater, aperture-for-aperture, than other Schmidt-Cassegrains utilizing standard-size primary mirrors. The optical design of the 4" Model 2045D is almost identical but does not include an oversize primary, since the effect in this case is small. -

List of Bright Nebulae Primary I.D. Alternate I.D. Nickname
List of Bright Nebulae Alternate Primary I.D. Nickname I.D. NGC 281 IC 1590 Pac Man Neb LBN 619 Sh 2-183 IC 59, IC 63 Sh2-285 Gamma Cas Nebula Sh 2-185 NGC 896 LBN 645 IC 1795, IC 1805 Melotte 15 Heart Nebula IC 848 Soul Nebula/Baby Nebula vdB14 BD+59 660 NGC 1333 Embryo Neb vdB15 BD+58 607 GK-N1901 MCG+7-8-22 Nova Persei 1901 DG 19 IC 348 LBN 758 vdB 20 Electra Neb. vdB21 BD+23 516 Maia Nebula vdB22 BD+23 522 Merope Neb. vdB23 BD+23 541 Alcyone Neb. IC 353 NGC 1499 California Nebula NGC 1491 Fossil Footprint Neb IC 360 LBN 786 NGC 1554-55 Hind’s Nebula -Struve’s Lost Nebula LBN 896 Sh 2-210 NGC 1579 Northern Trifid Nebula NGC 1624 G156.2+05.7 G160.9+02.6 IC 2118 Witch Head Nebula LBN 991 LBN 945 IC 405 Caldwell 31 Flaming Star Nebula NGC 1931 LBN 1001 NGC 1952 M 1 Crab Nebula Sh 2-264 Lambda Orionis N NGC 1973, 1975, Running Man Nebula 1977 NGC 1976, 1982 M 42, M 43 Orion Nebula NGC 1990 Epsilon Orionis Neb NGC 1999 Rubber Stamp Neb NGC 2070 Caldwell 103 Tarantula Nebula Sh2-240 Simeis 147 IC 425 IC 434 Horsehead Nebula (surrounds dark nebula) Sh 2-218 LBN 962 NGC 2023-24 Flame Nebula LBN 1010 NGC 2068, 2071 M 78 SH 2 276 Barnard’s Loop NGC 2149 NGC 2174 Monkey Head Nebula IC 2162 Ced 72 IC 443 LBN 844 Jellyfish Nebula Sh2-249 IC 2169 Ced 78 NGC Caldwell 49 Rosette Nebula 2237,38,39,2246 LBN 943 Sh 2-280 SNR205.6- G205.5+00.5 Monoceros Nebula 00.1 NGC 2261 Caldwell 46 Hubble’s Var. -

Meeting Program
A A S MEETING PROGRAM 211TH MEETING OF THE AMERICAN ASTRONOMICAL SOCIETY WITH THE HIGH ENERGY ASTROPHYSICS DIVISION (HEAD) AND THE HISTORICAL ASTRONOMY DIVISION (HAD) 7-11 JANUARY 2008 AUSTIN, TX All scientific session will be held at the: Austin Convention Center COUNCIL .......................... 2 500 East Cesar Chavez St. Austin, TX 78701 EXHIBITS ........................... 4 FURTHER IN GRATITUDE INFORMATION ............... 6 AAS Paper Sorters SCHEDULE ....................... 7 Rachel Akeson, David Bartlett, Elizabeth Barton, SUNDAY ........................17 Joan Centrella, Jun Cui, Susana Deustua, Tapasi Ghosh, Jennifer Grier, Joe Hahn, Hugh Harris, MONDAY .......................21 Chryssa Kouveliotou, John Martin, Kevin Marvel, Kristen Menou, Brian Patten, Robert Quimby, Chris Springob, Joe Tenn, Dirk Terrell, Dave TUESDAY .......................25 Thompson, Liese van Zee, and Amy Winebarger WEDNESDAY ................77 We would like to thank the THURSDAY ................. 143 following sponsors: FRIDAY ......................... 203 Elsevier Northrop Grumman SATURDAY .................. 241 Lockheed Martin The TABASGO Foundation AUTHOR INDEX ........ 242 AAS COUNCIL J. Craig Wheeler Univ. of Texas President (6/2006-6/2008) John P. Huchra Harvard-Smithsonian, President-Elect CfA (6/2007-6/2008) Paul Vanden Bout NRAO Vice-President (6/2005-6/2008) Robert W. O’Connell Univ. of Virginia Vice-President (6/2006-6/2009) Lee W. Hartman Univ. of Michigan Vice-President (6/2007-6/2010) John Graham CIW Secretary (6/2004-6/2010) OFFICERS Hervey (Peter) STScI Treasurer Stockman (6/2005-6/2008) Timothy F. Slater Univ. of Arizona Education Officer (6/2006-6/2009) Mike A’Hearn Univ. of Maryland Pub. Board Chair (6/2005-6/2008) Kevin Marvel AAS Executive Officer (6/2006-Present) Gary J. Ferland Univ. of Kentucky (6/2007-6/2008) Suzanne Hawley Univ. -

X-Ray Super-Flares from Pre-Main Sequence Stars: Flare Energetics and Frequency
Draft version May 12, 2021 Typeset using LATEX twocolumn style in AASTeX63 X-ray Super-Flares From Pre-Main Sequence Stars: Flare Energetics And Frequency Konstantin V. Getman1 and Eric D. Feigelson1, 2 1Department of Astronomy & Astrophysics Pennsylvania State University 525 Davey Laboratory University Park, PA 16802, USA 2Center for Exoplanetary and Habitable Worlds (Accepted for publication in ApJ, May 2021) ABSTRACT Solar-type stars exhibit their highest levels of magnetic activity during their early convective pre- main sequence (PMS) phase of evolution. The most powerful PMS flares, super-flares and mega-flares, −1 have peak X-ray luminosities of log(LX ) = 30:5−34:0 erg s and total energies log(EX ) = 34−38 erg. Among > 24; 000 X-ray selected young (t . 5 Myr) members of 40 nearby star-forming regions from our earlier Chandra MYStIX and SFiNCs surveys, we identify and analyze a well-defined sample of 1,086 X-ray super-flares and mega-flares, the largest sample ever studied. Most are considerably more powerful than optical/X-ray super-flares detected on main sequence stars. This study presents energy estimates of these X-ray flares and the properties of their host stars. These events are produced by young stars of all masses over evolutionary stages ranging from protostars to diskless stars, with the occurrence rate positively correlated with stellar mass. Flare properties are indistinguishable for disk- bearing and diskless stars indicating star-disk magnetic fields are not involved. A slope α ' 2 in the −α flare energy distributions dN=dEX / EX is consistent with those of optical/X-ray flaring from older stars and the Sun. -

Open Clusters
Open Clusters Open clusters (also known as galactic clusters) are of tremendous importance to the science of astronomy, if not to astrophysics and cosmology generally. Star clusters serve as the "laboratories" of astronomy, with stars now all at nearly the same distance and all created at essentially the same time. Each cluster thus is a running experiment, where we can observe the effects of composition, age, and environment. We are hobbled by seeing only a snapshot in time of each cluster, but taken collectively we can understand their evolution, and that of their included stars. These clusters are also important tracers of the Milky Way and other parent galaxies. They help us to understand their current structure and derive theories of the creation and evolution of galaxies. Just as importantly, starting from just the Hyades and the Pleiades, and then going to more distance clusters, open clusters serve to define the distance scale of the Milky Way, and from there all other galaxies and the entire universe. However, there is far more to the study of star clusters than that. Anyone who has looked at a cluster through a telescope or binoculars has realized that these are objects of immense beauty and symmetry. Whether a cluster like the Pleiades seen with delicate beauty with the unaided eye or in a small telescope or binoculars, or a cluster like NGC 7789 whose thousands of stars are seen with overpowering wonder in a large telescope, open clusters can only bring awe and amazement to the viewer. These sights are available to all.