The State of Randomness in Current Java Implementations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Post-Apocalyptic Sun.Misc.Unsafe World
A Post-Apocalyptic sun.misc.Unsafe World http://www.superbwallpapers.com/fantasy/post-apocalyptic-tower-bridge-london-26546/ Chris Engelbert Twitter: @noctarius2k Jatumba! 2014, 2015, 2016, … Disclaimer This talk is not going to be negative! Disclaimer But certain things are highly speculative and APIs or ideas might change by tomorrow! sun.misc.Scissors http://www.underwhelmedcomic.com/wp-content/uploads/2012/03/runningdude.jpg sun.misc.Unsafe - What you (don’t) know sun.misc.Unsafe - What you (don’t) know • Internal class (sun.misc Package) sun.misc.Unsafe - What you (don’t) know • Internal class (sun.misc Package) sun.misc.Unsafe - What you (don’t) know • Internal class (sun.misc Package) • Used inside the JVM / JRE sun.misc.Unsafe - What you (don’t) know • Internal class (sun.misc Package) • Used inside the JVM / JRE // Unsafe mechanics private static final sun.misc.Unsafe U; private static final long QBASE; private static final long QLOCK; private static final int ABASE; private static final int ASHIFT; static { try { U = sun.misc.Unsafe.getUnsafe(); Class<?> k = WorkQueue.class; Class<?> ak = ForkJoinTask[].class; example: QBASE = U.objectFieldOffset (k.getDeclaredField("base")); java.util.concurrent.ForkJoinPool QLOCK = U.objectFieldOffset (k.getDeclaredField("qlock")); ABASE = U.arrayBaseOffset(ak); int scale = U.arrayIndexScale(ak); if ((scale & (scale - 1)) != 0) throw new Error("data type scale not a power of two"); ASHIFT = 31 - Integer.numberOfLeadingZeros(scale); } catch (Exception e) { throw new Error(e); } } } sun.misc.Unsafe -

Openjdk – the Future of Open Source Java on GNU/Linux
OpenJDK – The Future of Open Source Java on GNU/Linux Dalibor Topić Java F/OSS Ambassador Blog aggregated on http://planetjdk.org Java Implementations Become Open Source Java ME, Java SE, and Java EE 2 Why now? Maturity Java is everywhere Adoption F/OSS growing globally Innovation Faster progress through participation 3 Why GNU/Linux? Values Freedom as a core value Stack Free Software above and below the JVM Demand Increasing demand for Java integration 4 Who profits? Developers New markets, new possibilities Customers More innovations, reduced risk Sun Mindshare, anchoring Java in GNU/Linux 5 License + Classpath GPL v2 Exception • No proprietary forks (for SE, EE) • Popular & trusted • Programs can have license any license • Compatible with • Improvements GNU/Linux remain in the community • Fostering adoption • FSFs license for GNU Classpath 6 A Little Bit Of History Jun 1996: Work on gcj starts Nov 1996: Work on Kaffe starts Feb 1998: First GNU Classpath Release Mar 2000: GNU Classpath and libgcj merge Dec 2002: Eclipse runs on gcj/Classpath Oct 2003: Kaffe switches to GNU Classpath Feb 2004: First FOSDEM Java Libre track Apr 2004: Richard Stallman on the 'Java Trap' Jan 2005: OpenOffice.org runs on gcj Mai 2005: Work on Harmony starts 7 Sun & Open Source Java RIs Juni 2005: Java EE RI Glassfish goes Open Source Mai 2006: First Glassfish release Mai 2006: Java announced to go Open Source November 2006: Java ME RI PhoneME goes Open Source November 2006: Java SE RI Hotspot und Javac go Open Source Mai 2007: The rest of Java SE follows suit 8 Status: JavaOne, Mai 2007 OpenJDK can be fully built from source, 'mostly' Open Source 25,169 Source code files 894 (4%) Binary files (“plugs”) 1,885 (8%) Open Source, though not GPLv2 The rest is GPLv2 (+ CP exception) Sun couldn't release the 4% back then as free software. -

Free Java Developer Room
Room: AW1.121 Free Java Developer Room Saturday 2008-02-23 14:00-15:00 Welcome to the Free Java Meeting Welcome and introduction to the projects, people and themes that make Rich Sands – Mark Reinhold – Mark up the Free Java Meeting at Fosdem. ~ GNU Classpath ~ OpenJDK Wielaard – Tom Marble 15:00-16:00 Mobile Java Take your freedom to the max! Make your Free Java mobile. Christian Thalinger - Guillaume ~ CACAO Embedded ~ PhoneME ~ Midpath Legris - Ray Gans 16:00-16:40 Women in Java Technology Female programmers are rare. Female Java programmers are even more Clara Ko - Linda van der Pal rare. ~ Duchess, Ladies in Java Break 17:00-17:30 Hacking OpenJDK & Friends Hear about directions in hacking Free Java from the front lines. Roman Kennke - Andrew Hughes ~ OpenJDK ~ BrandWeg ~ IcePick 17:30-19:00 VM Rumble, Porting and Architectures Dalibor Topic - Robert Lougher - There are lots of runtimes able to execute your java byte code. But which Peter Kessler - Ian Rogers - one is the best, coolest, smartest, easiest portable or just simply the most fun? ~ Kaffe ~ JamVM ~ HotSpot ~ JikesRVM ~ CACAO ~ ikvm ~ Zero- Christian Thalinger - Jeroen Frijters assembler Port ~ Mika - Gary Benson - Chris Gray Sunday 2008-02-24 9:00-10:00 Distro Rumble So which GNU/Linux distribution integrates java packages best? Find out Petteri Raty - Tom Fitzsimmons - during this distro shootout! ~ Gentoo ~ Fedora ~ Debian ~ Ubuntu Matthias Klose 10:00-11:30 The Free Java Factory OpenJDK and IcedTea, how are they made and how do you test them? David Herron - Lillian Angel - Tom ~ OpenJDK ~ IcedTea Fitzsimmons 11:30-13:00 JIT Session: Discussion Topics Dynamically Loaded Want to hear about -- or talk about -- something the Free Java world and don't see a topic on the agenda? This time is reserved for late binding Tom Marble discussion. -

Eclipse (Software) 1 Eclipse (Software)
Eclipse (software) 1 Eclipse (software) Eclipse Screenshot of Eclipse 3.6 Developer(s) Free and open source software community Stable release 3.6.2 Helios / 25 February 2011 Preview release 3.7M6 / 10 March 2011 Development status Active Written in Java Operating system Cross-platform: Linux, Mac OS X, Solaris, Windows Platform Java SE, Standard Widget Toolkit Available in Multilingual Type Software development License Eclipse Public License Website [1] Eclipse is a multi-language software development environment comprising an integrated development environment (IDE) and an extensible plug-in system. It is written mostly in Java and can be used to develop applications in Java and, by means of various plug-ins, other programming languages including Ada, C, C++, COBOL, Perl, PHP, Python, Ruby (including Ruby on Rails framework), Scala, Clojure, and Scheme. The IDE is often called Eclipse ADT for Ada, Eclipse CDT for C/C++, Eclipse JDT for Java, and Eclipse PDT for PHP. The initial codebase originated from VisualAge.[2] In its default form it is meant for Java developers, consisting of the Java Development Tools (JDT). Users can extend its abilities by installing plug-ins written for the Eclipse software framework, such as development toolkits for other programming languages, and can write and contribute their own plug-in modules. Released under the terms of the Eclipse Public License, Eclipse is free and open source software. It was one of the first IDEs to run under GNU Classpath and it runs without issues under IcedTea. Eclipse (software) 2 Architecture Eclipse employs plug-ins in order to provide all of its functionality on top of (and including) the runtime system, in contrast to some other applications where functionality is typically hard coded. -

Installing Open Java Development Kit – Ojdkbuild for Windows
Installing Open Java Development Kit – ojdkbuild for Windows © IZUM, 2019 IZUM, COBISS, COMARC, COBIB, COLIB, CONOR, SICRIS, E-CRIS are registered trademarks owned by IZUM. CONTENTS 1 Introduction ......................................................................................................... 1 2 OpenJDK distribution .......................................................................................... 1 3 Removing Oracle Java ......................................................................................... 2 4 Installing OJDK – 32bit or 64bit, IcedTea Java .................................................. 3 5 Installing the COBISS3 interface ........................................................................ 7 6 Launching the COBISS3 interface .................................................................... 11 7 COBISS3 interface as a trusted source in IcedTea ojdkbuild ........................... 11 © IZUM, 16. 7. 2019, VOS-NA-EN-380, V1.0 i VOS Installing Open Java Development Kit – ojdkbuild for Windows 1 Introduction At the end of 2018 Oracle announced a new business policy for Java SE which entered into force in April 2019. That is why when you install Java a notification and warning window appears. All versions of Java from 8 u201 onwards not intended for personal use are payable. For this reason, we suggest you do not update Java 8 to a newer version for work purposes. If you want a newer version of Java 8, install OpenJDK 8 and IcedTea. Also, do not install Java 8 on new computers (clients), but install OpenJDK 8 with IcedTea support. 2 OpenJDK distribution OpenJDK 1.8. build for Windows and Linux is available at the link https://github.com/ojdkbuild/ojdkbuild. There you will find versions for the installation. The newest version is always at the top, example from 7 May 2019: © IZUM, 16. 7. 2019, VOS-NA-EN-380, V1.0 1/11 Installing Open Java Development Kit – ojdkbuild for Windows VOS 3 Removing Oracle Java First remove the Oracle Java 1.8 software in Control Panel, Programs and Features. -

Openjdk 8 Getting Started with Openjdk 8 Legal Notice
OpenJDK 8 Getting started with OpenJDK 8 Last Updated: 2021-07-21 OpenJDK 8 Getting started with OpenJDK 8 Legal Notice Copyright © 2021 Red Hat, Inc. The text of and illustrations in this document are licensed by Red Hat under a Creative Commons Attribution–Share Alike 3.0 Unported license ("CC-BY-SA"). An explanation of CC-BY-SA is available at http://creativecommons.org/licenses/by-sa/3.0/ . In accordance with CC-BY-SA, if you distribute this document or an adaptation of it, you must provide the URL for the original version. Red Hat, as the licensor of this document, waives the right to enforce, and agrees not to assert, Section 4d of CC-BY-SA to the fullest extent permitted by applicable law. Red Hat, Red Hat Enterprise Linux, the Shadowman logo, the Red Hat logo, JBoss, OpenShift, Fedora, the Infinity logo, and RHCE are trademarks of Red Hat, Inc., registered in the United States and other countries. Linux ® is the registered trademark of Linus Torvalds in the United States and other countries. Java ® is a registered trademark of Oracle and/or its affiliates. XFS ® is a trademark of Silicon Graphics International Corp. or its subsidiaries in the United States and/or other countries. MySQL ® is a registered trademark of MySQL AB in the United States, the European Union and other countries. Node.js ® is an official trademark of Joyent. Red Hat is not formally related to or endorsed by the official Joyent Node.js open source or commercial project. The OpenStack ® Word Mark and OpenStack logo are either registered trademarks/service marks or trademarks/service marks of the OpenStack Foundation, in the United States and other countries and are used with the OpenStack Foundation's permission. -

Fedora Core, Java™ and You
Fedora Core, Java™ and You Gary Benson Software Engineer What is Java? The word ªJavaº is used to describe three things: The Java programming language The Java virtual machine The Java platform To support Java applications Fedora needs all three. What Fedora uses: GCJ and ECJ GCJ is the core of Fedora©s Java support: GCJ includes gcj, a compiler for the Java programming language. GCJ also has a runtime and class library, collectively called libgcj. The class library is separately known as GNU Classpath. ECJ is the Eclipse Compiler for Java: GCJ©s compiler gcj is not used for ªtraditionalº Java compilation. More on that later... Why libgcj? There are many free Java Virtual machines: Cacao, IKVM, JamVM, Jikes RVM, Kaffe, libgcj, Sable VM, ... There are two main reasons Fedora uses libgcj: Availability on many platforms. Ability to use precompiled native code. GNU Classpath Free core class library for Java virtual machines and compilers. The JPackage Project A collection of some 1,600 Java software packages for Linux: Distribution-agnostic RPM packages. Both runtimes/development kits and applications. Segregation between free and non-free packages. All free packages built entirely from source. Multiple runtimes/development kits may be installed. Fedora includes: JPackage-compatible runtime and development kit packages. A whole bunch of applications. JPackage JOnAS Fedora©s Java Compilers gcj can operate in several modes: Java source (.java) to Java bytecode (.class) Java source (.java) to native machine code (.o) Java bytecode (.class, .jar) to native machine code (.o) In Fedora: ECJ compiles Java source to bytecode. gcj compiles that bytecode to native machine code. -

Openjdk 11 Getting Started with Openjdk 11 Legal Notice
OpenJDK 11 Getting started with OpenJDK 11 Last Updated: 2021-07-21 OpenJDK 11 Getting started with OpenJDK 11 Legal Notice Copyright © 2021 Red Hat, Inc. The text of and illustrations in this document are licensed by Red Hat under a Creative Commons Attribution–Share Alike 3.0 Unported license ("CC-BY-SA"). An explanation of CC-BY-SA is available at http://creativecommons.org/licenses/by-sa/3.0/ . In accordance with CC-BY-SA, if you distribute this document or an adaptation of it, you must provide the URL for the original version. Red Hat, as the licensor of this document, waives the right to enforce, and agrees not to assert, Section 4d of CC-BY-SA to the fullest extent permitted by applicable law. Red Hat, Red Hat Enterprise Linux, the Shadowman logo, the Red Hat logo, JBoss, OpenShift, Fedora, the Infinity logo, and RHCE are trademarks of Red Hat, Inc., registered in the United States and other countries. Linux ® is the registered trademark of Linus Torvalds in the United States and other countries. Java ® is a registered trademark of Oracle and/or its affiliates. XFS ® is a trademark of Silicon Graphics International Corp. or its subsidiaries in the United States and/or other countries. MySQL ® is a registered trademark of MySQL AB in the United States, the European Union and other countries. Node.js ® is an official trademark of Joyent. Red Hat is not formally related to or endorsed by the official Joyent Node.js open source or commercial project. The OpenStack ® Word Mark and OpenStack logo are either registered trademarks/service marks or trademarks/service marks of the OpenStack Foundation, in the United States and other countries and are used with the OpenStack Foundation's permission. -
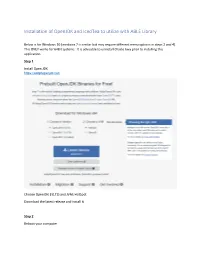
Installation of Openjdk and Icedtea to Utilize with ABLE Library
Installation of OpenJDK and IcedTea to utilize with ABLE Library Below is for Windows 10 (windows 7 is similar but may require different menu options in steps 2 and 4). This ONLY works for 64Bit systems. It is advisable to uninstall Oracle Java prior to installing this application. Step 1 Install Open JDK https://adoptopenjdk.net/ Choose OpenJDK 8 (LTS) and JVM: HotSpot Download the latest release and Install it Step 2 Reboot your computer Step 3 Run your JNLP file by clicking your link OR by double clicking on the JNLP file on your desktop. You should see the IcedTea loading window before the Java application starts up. If you do NOT see the IcedTea loading window AND you have Oracle Java installed: 1. Right click on your JNLP file and choose Open With 2. 3. Select Choose another app 4. If you see javaws.exe in your list choose this (do not choose Java™ Web Launcher (this is the Oracle version of Java) 5. If you do NOT see javaws.exe as an option choose More Apps and scroll to the bottom and click on the Use Another App on this PC link 6. Browse to: C:\Program Files\IcedTeaWeb\WebStart\bin in the window that opens and choose javaws.exe and click Open 7. The next time you to this javaws.exe should be in your menu as an option – you can also choose Always Use this app the next time and you should be able to double click a JNLP file to open using IcedTea Web Remember the OpenJDK will ONLY work on the JNLP files with “Open” in the name – this helps to differentiate between the standard JNLP files and the ones that work with OpenJDK. -

FOSDEM 2006 – Saturday 25Th February (Part 1) 1/6
FOSDEM 2006 – Saturday 25th February (part 1) 1/6 10:00 OpenGroupware ▼ Opening Talks Tutorials KDE openSUSE Embedded Mozilla Tcl/Tk 13:00 (Janson) (H2215/Ferrer) (H.1301) (H.1302) (H.1308) (H.1309) +GNUstep (H.2111) (AW1.105) 13:00 lunch break 13:00 Movitation, 13:00 Opening and GNUstep devtools: Goals and 13:15 13:15 introduction GORM, StepTalk Opportunities Axel Hecht Nicolas Roard Systems VoIP 13:30 DTrace S. Krause-Harder, SETR LiveCD 13:30 M. Loeffler (Janson) (Lameere) 13:45 Jon Haslam Hector Oron 13:45 Mozilla 14:00 14:00 Kubuntu openSUSE Build 14:00 Foundation CoreData Intro to Plan9 SER Service Intro 14:15 14:15 Jonathan 14:15 G. Markham Sašo Kiselkov Tcl/Tk Uriel M. Jan Janak A. Schroeter, 14:30 Pereira 14:30 Ridell C. Schumacher, Optimizing 14:30 Mozilla Clif Flynt A. Bauer 14:45 14:45 Linux kernel 14:45 Europe 15:00 15:00 Open SUSE Linux and apps 15:00 Tristan Nitot Web applicationsGUI for DTrace Asterisk M.Opdenacker 15:15 Jon Haslam Mark 15:15 Key Devroom Power Mngmt 15:15 SeaMonkey with SOPE ASIC 15:30 Spencer 15:30 Signing Timo Hoenig, Lock-free data 15:30 Project Marcus Mueller verification 15:45 15:45 Holger Macht exchange for 15:45 Robert Kaiser Karel Nijs Real-Time apps 16:00 16:00 SUSE Linux 16:00 Xen Speex Asterisk Marketing Peter Soetens Flock GNUstep on the Hecl: 10.2: 16:15 Ian Pratt J.-M. Valin 16:15 Mark KDE 16:15 Z. Braniecki Zaurus PDA scripting Quo vadis ? 16:30 16:30 Spencer Sebastian Alsa SoC layer16:30 Nicolaus Schaller for mobiles Kügler M.Loeffler,C.Thiel D.N.Welton 16:45 16:45 Liam Girdwood 16:45 Mozilla 17:00 Closing Talks (Janson) 17:00 17:00 Project BOF 17:15 17:15 17:15 FOSDEM Donators Return 17:30 17:30 17:45 17:45 17:30 FSF Europe Opening Talks (Janson) Hacker Rooms LPI Exam Sessions 10:00 FOSDEM Core Staff Welcome Speech Building H: H2213 Saturday 13:00-14:30 10:30 Keynote Building AW: AW1.117 (H2214) 15:00-16:30 Richard M. -
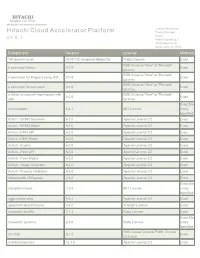
Hitachi Cloud Accelerator Platform Product Manager HCAP V 1
HITACHI Inspire the Next 2535 Augustine Drive Santa Clara, CA 95054 USA Contact Information : Hitachi Cloud Accelerator Platform Product Manager HCAP v 1 . 5 . 1 Hitachi Vantara LLC 2535 Augustine Dr. Santa Clara CA 95054 Component Version License Modified 18F/domain-scan 20181130-snapshot-988de72b Public Domain Exact BSD 3-clause "New" or "Revised" a connector factory 0.0.9 Exact License BSD 3-clause "New" or "Revised" a connector for Pageant using JNA 0.0.9 Exact License BSD 3-clause "New" or "Revised" a connector for ssh-agent 0.0.9 Exact License a library to use jsch-agent-proxy with BSD 3-clause "New" or "Revised" 0.0.9 Exact sshj License Exact,Ma activesupport 5.2.1 MIT License nually Identified Activiti - BPMN Converter 6.0.0 Apache License 2.0 Exact Activiti - BPMN Model 6.0.0 Apache License 2.0 Exact Activiti - DMN API 6.0.0 Apache License 2.0 Exact Activiti - DMN Model 6.0.0 Apache License 2.0 Exact Activiti - Engine 6.0.0 Apache License 2.0 Exact Activiti - Form API 6.0.0 Apache License 2.0 Exact Activiti - Form Model 6.0.0 Apache License 2.0 Exact Activiti - Image Generator 6.0.0 Apache License 2.0 Exact Activiti - Process Validation 6.0.0 Apache License 2.0 Exact Addressable URI parser 2.5.2 Apache License 2.0 Exact Exact,Ma adzap/timeliness 0.3.8 MIT License nually Identified aggs-matrix-stats 5.5.1 Apache License 2.0 Exact agronholm/pythonfutures 3.3.0 3Delight License Exact ahoward's lockfile 2.1.3 Ruby License Exact Exact,Ma ahoward's systemu 2.6.5 Ruby License nually Identified GNU Lesser General Public License ai's -

Contributing to Eclipse: a Case Study
Contributing to Eclipse: A Case Study Henttonen Katja, Matinlassi Mari VTT Technical Research Centre of Finland P.O. Box 1100, 90571 Oulu, Finland {Katja.Henttonen, Mari.Matinlassi}@vtt.fi Abstract: Open source software has gained a lot of well•deserved attention during the last few years. Eclipse is one of the most successful open source communities providing an open development environment and an application lifecycle platform. The main aim of this paper is to describe a case study on contributing to the Eclipse open source community and report experiences. The most important experiences are related to building an architecture model repository tool as an Eclipse plug•in and starting a new community around it. 1 Introduction Open source software (OSS) has been growing its popularity among software developers, communities and media over a decade and lately also the research community has been active in studying the subject. Among the most successful open source projects, Eclipse (www.eclipse.org) is an open development platform and application framework for building software. The Eclipse community has distinguished itself in productivity and creativity [Ki05] and has developed new features that have evolved Eclipse towards a platform that is integrating not only tools but also applications and services [Gr05]. The new features also make Eclipse a strong force in the embedded market [Er06] [Kl05] and make the community even more international [La05]. There are several ways of contributing to open source communities, e.g. fixing bugs and providing new features. In this paper, contributing to Eclipse is considered as a twofold issue. On the one hand, a contribution, i.e.