DOCSLIB.ORG

Essays on Monetary Policy and Bitcoin Financial Economics Kyle Lance Rechard Clemson University, [email protected]

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Essays on Monetary Policy and Bitcoin Financial Economics Kyle Lance Rechard Clemson University, Krechar@Clemson.Edu View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Clemson University: TigerPrints Clemson University TigerPrints All Dissertations Dissertations May 2019 Essays on Monetary Policy and Bitcoin Financial Economics Kyle Lance Rechard Clemson University, [email protected] Follow this and additional works at: https://tigerprints.clemson.edu/all_dissertations Recommended Citation Rechard, Kyle Lance, "Essays on Monetary Policy and Bitcoin Financial Economics" (2019). All Dissertations. 2367. https://tigerprints.clemson.edu/all_dissertations/2367 This Dissertation is brought to you for free and open access by the Dissertations at TigerPrints. It has been accepted for inclusion in All Dissertations by an authorized administrator of TigerPrints. For more information, please contact [email protected]. ESSAYS ON MONETARY POLICY AND BITCOIN FINANCIAL ECONOMICS A Dissertation Presented to the Graduate School of Clemson University In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy Economics by Kyle Rechard May 2019 Accepted by: Dr. Gerald P. Dwyer, Jr., Committee Chair Dr. Robert Tamura Dr. Michal Jerzmanowki Dr. Scott Baier Abstract This dissertation includes three chapters. The first chapter investigates the impact of the Federal Reserve’s balance sheet normalization using a Bayesian vector autoregression (BVAR) framework. I use counterfactual conditional forecasts to find that a reduction in asset holdings down to a level where the federal funds market is active again will reducereal GDP growth by an average of 0.18 percent per year and core inflation by a non-significant average of 0.07 percent per year under Quantitative Tightening, relative to a scenario where the Federal Reserve maintains a constant dollar amount of assets until 2024. The second chapter models monetary policy using Taylor’s rule for the nominal interest- rate target and examines the difference between the actual Federal Funds Rate and the Tay- lor Rule model of behavior for distinct structural changes. Both a simple factor ANOVA and regime switching methods find that there were “tight” or “loose” regimes in U.S. mon- etary policy over the period 1965 to 2008. However, after accounting for the change in inflation measurement from CPI to PCE and then core PCE after 2004, Alan Greenspan’s tenure from 2003 to 2006 is consistent with his earlier symmetric deviations from the Tay- lor Rule. The final chapter examines the volatility of Bitcoin exchange rates which have gained a great deal of attention since the creation of the currency. Standard measures of volatility reflect the dramatic change in the Bitcoin/US dollar exchange rate, from about $0.05 USD in 2010 to the neighborhood of $20,000 USD at the end of 2017, and down to around ii $5,000 USD in mid-2019. Characterizing the short-term and long-term volatility gives an impression of the volatility of Bitcoin compared to other assets, as well as implying the viability of Bitcoin as a medium of exchange and alternative asset. iii Acknowledgements This dissertation has been greatly improved by the contributions of many people. First and foremost, I would like to thank my advisor, Dr. Gerald Dwyer, for his constant guid- ance throughout the entire process. Without his time and dedication, much of this disser- tation would not have been possible. I would also like to thank the other members of my committee, Dr. Robert Tamura, Dr. Michal Jerzmanowski, and Dr. Scott Baier, for their helpful comments and suggestions, as well as the participants in the Macro workshop at Clemson. The tips and comments I received while presenting in the workshop were instru- mental in shaping my research. I would like to thank Dr. John Deveraux, and Dr. Juan Rubio-Ramirez who were willing to read my work, and provide detailed feedback. I am also extremely grateful to Dr. Sam Standert for his feedback. Next, I would like to thank my family for their love and support. My parents, Rob and Pat Rechard, have been been a constant source of love and encouragment. I would not have accomplished this if it were not for them. Finally, I would like to thank the graduate students at Clemson. My classmatesOur helped shape my love for economics, and the friendships and fun experiences we’ve had are memories I’ll always carry with me. In particular, I am thankful for my officemate, Jacob Walloga, and roomate Ben Harbolt for all the fun conversations. All remaining errors are my own. iv Contents Title Page ...................................... i Abstract ....................................... ii Acknowledgements ................................. iv List of Tables .................................... vii List of Figures ................................... ix 1 Quantitative Tightening: What are the macroeconomic consequences of re- ducing the Federal Reserve Balance Sheet? ................... 1 1.1 Introduction . 1 1.2 Review of the Literature . 2 1.2.1 Quantitative Easing . 2 1.2.2 Quantitative Tightening . 5 1.3 Empirical Approach . 9 1.3.1 Identification . 13 1.4 Estimation and Inference . 16 1.4.1 Counterfactual Forecasting . 18 1.5 Results . 20 1.5.1 Robustness . 24 v 1.6 Conclusion . 26 1.7 Appendix . 28 2 Greenspan didn’t cause the Great Recession: Examining Federal Reserve Chairmen Deviations from the Taylor Rule ................... 33 2.1 Introduction . 33 2.2 Previous Literature . 35 2.3 Data . 36 2.3.1 Real Time Taylor Rule . 37 2.4 Empirical Methodology . 40 2.5 Results . 42 2.6 Conclusion . 46 3 Long-run and Short-run Volatility in Bitcoin’s Price .............. 50 3.1 Introduction . 50 3.2 Volatility of Bitcoin . 51 3.2.1 Volatility Calculation . 52 3.3 Short-run and Long-run Variance Decompositions . 53 3.3.1 Changes in Mean Over Time . 53 3.3.2 The Local Linear Trend Model . 56 3.4 Variance Decompositions of Bitcoin . 57 3.5 Conclusion . 59 Bibliography . 60 vi List of Tables 1.1 OLS Estimation: Non-Linear Coefficients . 13 1.2 Security Purchase Shock Sign Restrictions . 16 1.3 Reverse QE I 2018-2024 Annualized Median Differential Effects: 2007- 2017 sample . 21 1.4 Reverse QE II 2018-2024 Annualized Differential Effects: 2007-2017 sam- ple....................................... 32 2.1 Tukey HSD:St. Louis Rule . 48 2.2 Tukey HSD: Bernanke Rule . 49 3.1 Changes in Mean Decomposition . 57 vii List of Figures 1.1 Federal Reserve Balance Sheet Trends . 7 1.2 Monetary Policy Instruments . 11 1.3 Securities Held Outright as a proportion of nominal GDP . 12 1.4 Perfect Foresight Conditional Forecasts: 2007-2017 sample . 22 1.5 Perfect Foresight Output and Inflation Conditional Forecasts: 2007-2017 sample . 25 1.6 The Data . 28 1.7 Asymmetric Impact of 1% Decline in Assets/GDP Ratio . 31 2.1 St. Louis Fed Taylor rule . 36 2.2 iF edF und;t − iT aylor;t: 1954-2008 . 37 2.3 Gap Version of Okun’s Law 1954-2008 . 39 2.4 Real-Time iF edF und;t − iSt:Louis;t, 1965-2008 . 39 2.5 Fitted Regimes with Fed Chairmen tenure periods, 1965-2008 . 42 2.6 Fitted Regimes using PCE rather than CPI inflation target from 2000 to 2008 44 2.7 Markov Switching: Regime 1 . 44 2.8 Markov Switching: Regime 2 . 45 2.9 Markov Switching: Regime 3 . 46 3.1 Log Scale Price Level . 51 3.2 Monthly Realized Volatility . 53 viii 3.3 Change-in-Mean Volatility Decomposition . 58 3.4 Bitcoin Realized Volatility Trend Decomposition . 59 ix Chapter 1 Quantitative Tightening: What are the macroeconomic consequences of reducing the Federal Reserve Balance Sheet? 1.1 Introduction What effects will Quantitative Tightening (QT), or Reverse Quantitative Easing have on the United States real economy and financial markets? If the U.S. Federal Reserve’s accumu- lation of a massive quantity of assets had an expansionary effect on the real economy and financial markets, will the plan to shrink the massive balance sheet have the opposite effect on the real U.S. economy and financial markets? For the Federal Reserve, the purpose of reducing security holdings is to eventually reduce the reserve holdings of banks and other entities held at the Federal Reserve to a level where overnight borrowings are needed by some entities to meet reserve require- 1 ments. Once this occurs, the federal funds rate will be the monetary policy instrument of the FOMC, as it was prior to 2008. This balance sheet “normalization” of the conduct of monetary policy will allow the Fed to discontinue the dual policy instrument structure it has operated under since 2008. In the current monetary policy framework, both Interest on Excess Reserves (IOER) and the level of security holdings are used to influence long- term interest rates and (more importantly) portfolio flows from the Treasury market into the private bond and equity markets (Minutes of the FOMC, July 29-30, 2014). In this paper I create a regime dependent, Bayesian structural vector autoregressive (VAR) model and forecast the differential outcome for real economy until December 2024, conditional on the proposed path of asset reduction or a counterfactual policy of maintain- ing a $4.2 trillion security holding portfolio. I find that reverse QE will result in an average of 0.18 percent less real GDP growth per year until 2024, comparing the conditional point forecasts for December 2024 to the forecast conditional on the Federal Reserve maintain- ing a constant dollar value of asset holdings until 2024. However, for both perfect foresight and structural forecasts, the average forecast difference is calculated from forecast variable levels in December 2024. The results are unaffected by shocks to the path of reductions, so long as the Federal Reserve still plans to normalize the balance sheet by the end of 2024. 1.2 Review of the Literature 1.2.1 Quantitative Easing The Federal Reserve’s response to the 2008-2009 financial crisis included large-scale asset purchases - buying government debt and mortgage backed securities (MBS) as a means to provide continued stimulus after the Federal Funds rate had been reduced near zero in November 2008.
Load more

Recommended publications
  • HOW DID QUANTITATIVE EASING REALLY WORK? a New Methodology for Measuring the Fed’S Impact on Financial Markets
    HOW DID QUANTITATIVE EASING REALLY WORK? A New Methodology for Measuring the Fed’s Impact on Financial Markets Ramin Toloui Stanford Institute for Economic Policy Research [email protected] SIEPR Working Paper No. 19-032 November 2019 ABSTRACT This paper introduces a new methodology for measuring the impact of unconventional policies. Specifically, the paper examines how such policies reshaped market perceptions of how the Fed would behave in the future—not merely the expected path for policy rates, but how the central bank would adjust that path in response to different combinations of future inflation and growth. In short, it studies how quantitative easing affected investor beliefs about the future policy reaction function. The paper (1) proposes a novel model of market expectations for the central bank’s future policy reaction function based on the Taylor Rule; (2) shows that empirical estimates of the model exhibit structural breaks that coincide with innovations in unconventional policies; and (3) finds that such policy innovations were associated with regime shifts in the behavior of 10-year U.S. Treasury yields, as well as unusual performance in risk assets such as credit spreads and equities. These findings provide evidence that a key causal channel for unconventional policies was via their impact on market expectations for the Fed’s future policy reaction function. These shifts in expectations, in turn, appear to have had larger, more persistent, and more pervasive effects across financial markets than found in previous studies. Monetary economics today is obsessed with balance sheets—and rightfully so. More than ten years after the global financial crisis, policy interest rates remain exceptionally low in much of the industrialized world.
    [Show full text]
  • The Accidental Bitcoiner
    OPINION PIECE The Accidental Bitcoiner JunE 2018 C O I N C O M P A S S . C O M Page 1 The Accidental Bitcoiner Through our daily research in the world of finance, geo-politics, and macro- economics we come across interviews and research papers where the author either inadvertently, or despite themselves and their objections present what we believe is a pro-Bitcoin argument. This week's 'Accidental Bitcoiner' is Michael Pento of Pento Portfolio Strategies. In an interview with Chris Martenson on Peak Prosperity Podcast, Mr Pento provides an in-depth analysis of Central Bank policies post-2008 and how the upcoming yield inversion will affect the global economic landscape. Mr Pento's opinions are summarised and we analyse that should his projections take effect, we believe this would lead to an appreciation of the value of Bitcoin. In this interview Mr Pento defines fiat currency as based on faith, unlike gold which is based on science. Mr Pento describes that it takes US$1,000 to remove an ounce of gold from the earth, so it has intrinsic value. The figure Mr Pento is referring to is the cost of gold production per troy ounce. That number is a rounded global numerator yet when one takes into consideration the parameters such as a mine’s location and national currencies, the most recent figures we’ve come across range from US$700 (Peruvian mine) to $US850 (USA mine) and US$1,200 for a mine in Australia. Mr Pento asserts, and we agree, that fiat currency is based on faith in that ‘they’ (governments, central banks) can print their own money.
    [Show full text]
  • THE CIO MONTHLY PERSPECTIVE Rockefeller Global Family Office January 6, 2021 45 Rockefeller Plaza, Floor 5 New York, NY 10111
    THE CIO MONTHLY PERSPECTIVE Rockefeller Global Family Office January 6, 2021 45 Rockefeller Plaza, Floor 5 New York, NY 10111 THE ROARING TWENTIES? Roaring growth in ‘21; roaring inflation down the road The CIO Monthly There was a rare celestial occurrence on Winter Solstice 2020 – the closest conjunction of Jupiter and Saturn in 397 years. On December 21st, the two planets were separated by a mere 0.1 degree and appeared as one shiny “star” on Perspective the evening sky. Some astrologers warned that the great conjunction would bring about cataclysmic events on Earth. However, it seemed that people had already suffered enough with much of the world mired in another wave of COVID-19 outbreak. In fact, investors have looked past the dark winter to a bright 2021 where stars appear perfectly aligned, thanks to the conjunction of new fiscal relief, effective vaccines, continued monetary largess from central banks, and the most supportive financial conditions in decades. This optimism has resulted in a powerful stock rally over the final two months of 2020 with the S&P 500 Index, Russell 2000® Index, and the MSCI EAFA Index January 6, 2021 soaring 15%, 28%, and 21%, respectively. It’s ironic that the worst health crisis and recession in decades have resulted in a solid year of gains for most financial assets. 2021 is likely to evolve into the strongest growth year since the late 1990s due to easy comparisons as well as outsized Jimmy C. Chang, CFA stimulus. Equities will likely march higher, especially during the first half of the year, as the market enters Chief Investment Officer arguably the best part of the business cycle – accelerating Rockefeller Global Family Office growth with continued support from fiscal and monetary (212) 549-5218 | [email protected] policies.
    [Show full text]
  • ABS/Securitized Credit: the Best Offense Is a Good Defense
    For Financial Intermediary, Institutional and Consultant use only. Not for redistribution under any circumstances. ABS/Securitized credit: the best offense is a good defense January 2019 By Michelle Russell-Dowe, Head of Securitized Credit As a child growing up during the ‘80s in Chicago, I always thought the adage was “the best offense is a good defense.” While, in fact, the adage as penned by George Washington was the opposite, as any good Chicago Bears fan knows…offense wins games and defense wins championships. I was particularly enamored by the cast of characters that made up the ’85 Bears, including the fact that they believed in their team and system of play to such an extent that they performed a music video “The Super Bowl Shuffle” before making the Super Bowl in 1985. At the end of the day, sitting at Soldier Field, freezing fans would cross their fingers and hope for the offense to leave the field, so the defense could come out. The Bears defense was a thing of beauty for two reasons: 1) they scored points 2) they left the team in great offensive field position. Surveying the current state of the market in general, we believe that playing a good defense, especially as market volatility has increased, makes sense. In fact, scoring a few points, and maintaining good field position for when you switch to offense, sounds much better than potentially losing ground. In this paper, we refer to the consumer segments (asset-backed securities, or ABS, and mortgage-backed securities, or MBS) as Main Street.
    [Show full text]
  • Implications of Quantitative Tightening and Investment-Grade Corporate Bonds
    Implications of Quantitative Tightening and Investment-Grade Corporate Bonds December 2018 Written by: Phil Gioia, CFA Ted Hospodar 333 S. Grand Ave., 18th Floor || Los Angeles, CA 90071 || (213) 633-8200 Implications of Quantitative Tightening and Investment-Grade Corporate Bonds Since the Global Financial Crisis of 2008, the U.S. Federal Reserve (Fed) has engaged in two unconventional monetary policies Key Takeaways known as Quantitative Easing (QE) and Quantitative Tightening In recent years, the Fed has undertaken unconventional monetary policy to stimulate the economy, mainly through (QT). QE is a policy whereby a central bank purchases financial large-scale asset purchase programs which has kept assets from banks and financial institutions to lower interest interest rates artificially low. rates. The goal is to stimulate the economy by increasing demand Corporate America has capitalized on historically low levels for existing securities, driving prices of these securities higher and of interest rates by issuing significantly more debt with thus yields lower; allowing entities to borrow money at lower longer maturities. In addition to the increase in amount of corporate bonds yields and increase market liquidity. This policy was implemented outstanding, the credit quality of the market has by the Fed on three separate occasions since the Global Financial deteriorated. Crisis; popularly known as QE1, QE2 and QE3. As a result, the Fed Investment-grade corporate bonds are trading near had accumulated roughly $4.5 trillion of U.S. Treasuries (UST) and historically low spreads. Agency Mortgage-Backed Securities (MBS) on its balance sheet The combination of longer duration in investment-grade corporate bonds, coupled with lower average credit quality upon QE’s conclusion.
    [Show full text]
  • Evaluating Central Banks' Tool
    Evaluating Central Banks' Tool Kit: Past, Present, and Future∗ Eric Sims Jing Cynthia Wu Notre Dame and NBER Notre Dame and NBER First draft: February 28, 2019 Current draft: May 21, 2019 Abstract We develop a structural DSGE model to systematically study the principal tools of unconventional monetary policy { quantitative easing (QE), forward guidance, and negative interest rate policy (NIRP) { as well as the interactions between them. To generate the same output response, the requisite NIRP and forward guidance inter- ventions are twice as large as a conventional policy shock, which seems implausible in practice. In contrast, QE via an endogenous feedback rule can alleviate the constraints on conventional policy posed by the zero lower bound. Quantitatively, QE1-QE3 can account for two thirds of the observed decline in the \shadow" Federal Funds rate. In spite of its usefulness, QE does not come without cost. A large balance sheet has consequences for different normalization plans, the efficacy of NIRP, and the effective lower bound on the policy rate. Keywords: zero lower bound, unconventional monetary policy, quantitative easing, negative interest rate policy, forward guidance, quantitative tightening, DSGE, Great Recession, effective lower bound ∗We are grateful to Todd Clark, Drew Creal, and Rob Lester, as well as seminar participants at the Federal Reserve Banks of Dallas and Cleveland and the University of Wisconsin-Madison, for helpful comments. Correspondence: [email protected], [email protected]. 1 Introduction In response to the Financial Crisis and ensuing Great Recession of 2007-2009, the Fed and other central banks pushed policy rates to zero (or, in some cases, slightly below zero).
    [Show full text]
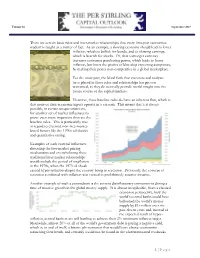
  • 1 | Page There Are Certain Basic Rules and Inter-Market
    Volume 83 September 2017 There are certain basic rules and inter-market relationships that every first-year economics student is taught as a matter of fact. As an example, a slowing economy should lead to lower inflation, which is bullish for bonds, and to slowing earnings, which is bearish for stocks. Or, that a stronger currency increases consumer purchasing power, which leads to lower inflation, but hurts the profits of blue chip exporting companies, by making their prices non-competitive in a global marketplace. For the most part, the blind faith that investors and analysts have placed in these rules and relationships has proven warranted, as they do normally provide useful insight into the future course of the capital markets. However, these baseline rules do have an inherent flaw, which is that none of their economic inputs operate in a vacuum. This means that it is always possible, in certain unique situations, for another set of market influences to prove even more important than are the baseline rules. This is particularly true in regard to external, non-free-market- based factors like the 1970s oil shocks and quantitative easing. Examples of such external influences distorting the free-market pricing mechanisms and overwhelming these traditional inter-market relationships would include the period of stagflation in the 1970s, when the 1973 oil shock caused hyper-inflation despite the country being in recession. Previously, the concept of recession combined with inflation was viewed as prohibitively counter-intuitive. Another example of such a conundrum is the current disinflationary environment during a time of massive growth in the global money supply.
    [Show full text]
  • Qexit Q&A: Everything You Ever Wanted to Know About the Exit
    Economic Research: QExit Q&A: Everything You Ever Wanted To Know About The Exit From Quantitative Easing S&P Global Chief Economist: Paul J Sheard, New York (1) 212-438-6262; [email protected] Table Of Contents What does QExit mean? So QExit has nothing to do with Grexit and Brexit, right? Is "exit" the right way to frame this issue? Why is this topic getting attention now? What is the right way to think about QExit? What is the right way to think about QE, then? Is a central bank's balance sheet just like any other balance sheet? What are the main components of a central bank's balance sheet, particularly on the liability side? What determines the size of a central bank's balance sheet in normal times? I'm getting lost--why does the central bank in normal times keep the actual level of reserves in line with minimum reserve requirements? Who or what determines the level of reserves? WWW.STANDARDANDPOORS.COM/RATINGSDIRECT AUGUST 17, 2017 1 1902185 | 301765622 Table Of Contents (cont.) Let me ask again, then, what's the right way to think about QE? How do you apply the understanding of QE to understand QExit? How do the balance-sheet mechanics of QExit work? Does QExit imply a wall of new debt issuance by the government and raise the specter of a funding squeeze? If QE was an exercise in rampant money printing, is QExit a process of money destruction, raising the specter of a credit crunch being triggered? What do empirical studies suggest about the effect of QE on the term premium? Will QExit lead to longer-term interest rates going
    [Show full text]
  • How to Teach Your Children About Investing
    Issue 47 / January 2019 FE Trustnet magazine How to teach your children about investing SELFIE DEFENCE BREXIT WOUNDS RINGING THE CHANGES Protecting your portfolio How our departure The best investment against youth trends could hit your pension strategy for every decade Fund, Pension, Trust / Sector Profile / Stockpicker / What I Bought Last Issue 47 / January 2019 Editor’s letter FE Trustnet magazine ust like with “the with them for years. ignore how changing underperformance has which fund he is using birds and the Cherry Reynard finds consumption patterns made it cheap, John to gain exposure to one How to teach your bees”, talking to out how to approach among the young are Blowers worries about of the defining trends of children about investing J your children about the subject in this disrupting established the impact of Brexit the 21st century. investment and finance month’s cover story. businesses. Meanwhile, on his pension and Enjoy reading, may not be the easiest Learning shouldn’t be I find out what has been LGIM’s Gavin Launder conversation you ever a one-way street for the best investment names three stocks SELFIE DEFENCE BREXIT WOUNDS RINGING THE CHANGES Protecting your portfolio How our departure The best investment against youth trends could hit your pension strategy for every decade have, but leaving them experienced investors, strategy in every decade. using digitalisation and Fund, Pension, Trust / Sector Profile / Stockpicker / What I Bought Last to their own devices however, and as Daniel In our regular automation to add value. ISSUE 47 can have unintended Lanyon discovers, columns, Adam Lewis Finally, Brewin Dolphin’s Anthony Luzio CREDITS consequences that stay they can’t afford to asks if Europe’s recent Rob Burgeman reveals Editor FE TRUSTNET MAGAZINE (FORMERLY INVESTAZINE) Contents IS PUBLISHED BY THE TEAM BEHIND FE TRUSTNET IN Data hub What I bought last SOHO, LONDON 12 Crunching the biggest trends Brewin Dolphin’s Rob Burgeman says Schroder WEBSITE: www.trustnet.com down into figures EMAIL: editorial@financialex- P.
    [Show full text]
  • Global-Market-Perspective-Q42017
    or professional investors only. October 2017 Contents Introduction .................................................................................................................................... 3 Asset allocation views: Multi-Asset Group ................................................................................ 4 Regional equity views .................................................................................................................... 7 Fixed income views ........................................................................................................................ 8 Alternatives views .......................................................................................................................... 9 Economic views ............................................................................................................................. 10 Global strategy: From QE to QT: the outlook for global liquidity? ...................................... 14 Seven-year asset class forecast returns 2017 update ........................................................... 20 Research note: Navigating the small cap premia over the cycle ........................................ 31 Market returns .............................................................................................................................. 36 Disclaimer ........................................................................................................................ Back page Editors: Keith Wade and Tina Fong Global Market
    [Show full text]
  • And Tactical Views @Tylermordy September 2017 the Legacy of Qe
    Tyler Mordy, President & CIO super trends [email protected] and tactical views @TylerMordy September 2017 The legacy of qe “It’s good to be king / if only for a while / to be there in velvet ... Yeah I’ll be king when dogs get wings / can I help it if I still dream from time to time?” - Tom Petty from the 1994 album Wildflowers SPEED READ → 2017 continues to be a year of massive asset and sector rotation. For the intrepid macro investor, this is our time. → Quantitative tightening (QT) is not the equal and opposite of QE. Compared to the fast moving dynamics of QE during the financial crisis (when central bankers were desperately trying to boost confidence in the entire financial system), QT will be a glacial affair that plays out over several years. → Every secular bear market has an intermission. If a counter-trend rally in the US dollar unfolds over the next few quarters, don’t be fooled if it gives a lively performance. → Broad fundamentals remain excellent in emerging markets and are primed for multi-year outperformance. However, EM stocks and bonds may experience temporary underperformance versus developed ones. → Trump’s sectoral impact will be substantial. However, he will have far less impact on the global economy than originally envisioned by markets. But it is now clear that reduced regulation will be the key support for business confidence, rather than lower taxes and public investment programs. 1 and tactical super trends views PART A: SUPER TRENDS (3-5 Year Outlook) Global Financial Crisis Anniversary: What Have We Learned? This year marks the tenth anniversary since the onsetof the global financial crisis, the credit crunch that changed the world and, in many ways, serves as a demarcation line in reshaping economies, financial markets, politics — even our culture.
    [Show full text]
  • Quantitative Easing: Entrance and Exit Strategies
    Quantitative Easing: Entrance and Exit Strategies Alan S. Blinder This article was originally presented as the Homer Jones Memorial Lecture, organized by the Federal Reserve Bank of St. Louis, St. Louis, Missouri, April 1, 2010. Federal Reserve Bank of St. Louis Review , November/December 2010, 92 (6), pp. 465-79. pparently, it can happen here. On easing is something aberrant. I adhere to that December 16, 2008, the Federal Open nomenclature here. Market Committee (FOMC), in an I begin by sketching the conceptual basis for effort to fight what was shaping up quantitative easing: why it might be appropriate Ato be the worst recession since 1937-38, reduced and how it is supposed to work. I then turn to the the federal funds rate to nearly zero. 1 From then Fed’s entrance strategy—which is presumably on, with all its conventional ammunition spent, in the past, and then to the Fed’s exit strategy— the Federal Reserve was squarely in the brave which is still mostly in the future. Both strate gies new world of quantitative easing . Chairman Ben invite some brief comparisons with the Japanese Bernanke tried to call the Fed’s new policies experience between 2001 and 2006. Finally, I “credit easing,” probably to differentiate them address some questions about central bank inde - from actions taken by the Bank of Japan (BOJ) pendence raised by quantitative easing before earlier in the decade, but the label did not stick. 2 briefly wrapping up. Roughly speaking, quantitative easing refers to changes in the composition and/or size of a central bank’s balance sheet that are designed to THE CONCEPTUAL BASIS ease liquidity and/or credit conditions.
    [Show full text]