DOCSLIB.ORG

Experimentally Demonstrated the Intrinsic Instability of the Fluorite-Type Zr Cation Network

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Experimentally Demonstrated the Intrinsic Instability of the Fluorite-Type Zr Cation Network 0246110 Rta(i) 1 1,2 l,4 1,6 1,l 2 22 Rta(i) Figure 2. Temperature dependence of Zr-FTfor pure orthorhombic zirconia Figure 3 Temperature dependence of Zr-0 shell in tetragonal zirconia solid solution Our study has experimentally demonstrated the intrinsic instability of the fluorite-type Zr cation network. Coherent scattering beween Conclusions central Zr ion and distant cations is weaker and vibration modes of the Zr-cation network are It is found that, for all of zirconia solid softer in tetragonal zirconia than in monoclmic, solutions studied, the dopant-oxygen distances are orthorhombic, or stabilized cubic zirconia. In si@icantly ddferent from the Zr-0 distances. addition, the outer foux oxygens in the 8-fold The dopant-cation distances, on the other hand, coordinated Zr-0 polyhedron are only loosely are usually very close to the Zr-Zr distance, solutions. A bonded and are subject to very large static and confirming the formation of solid dynamic distortions. This effect is illustrated by general structural picture for zirconia solid the expanded portion of the Fourier transform solutions is one that places the dopant cations shown in Figure 3. randomly on tbe Zr sites in the cation network, but with distorted and sometimes very different Dopant Structure dopant-oxygen polyhedra surrounding these dopants. In the case of Ge4+ doping and Y-Nb We have also successfully performed co-doping, short-rangecation ordering has been EXAFS experiments at the dopant absorption suggested from our EXAFS results. edges for doped zirconia solid solutions. Dopants Based on the above structural information studied include the Ce-,Nb-, and Y-K edges as and other EXAFS results obtained from NSLS, well as Ce-LIn edge. In particular, we have we are beginning to obtain a complete picture of obtained Nb EXAFS data with a very high the atomistic origins of phase stabilization in signaYnoise ratio using the SSRL Ge detector zirconia. array. This experiment was essentially impossible using a conventional fluorescnece ion Acknowledgements chamber due to the very strong absorption of Zr at Nb-K edge energy. Analysis of these data is in Supported in part by a grant from the NSF progress. (DMR-8807024). 00232471 107 Proposal 2 17 1M Reconstructions and Structural Transitions of the CaF2/Si(lll) Interface C. A. Lucas, G.C. L. Wong* and D. Loretto Center for Advanced Materials, Materials Sciences Division, Lawrence Berkeley Laboratory, University of California, Berkeley, CA 94720. *and Department of Physics, University of California. Berkeley. CA 94720. Introduction growth rate of -1 CaFz triplc layer (TL) per 30 seconds. At 720°C CaF2 films with a thickness of -7TL's (-22A) CaFgSi (11 1) is a prototypical system for studying were grown. This is blow the critical thickness for atomic and electronic structure at the ionic/covalent strained layer growth (-12TL's). The sample was then interface. As a consequence there has been a wide range cooled to room tcmpcrature where, due to the smaller of experiments aimed at determining the interface lattice mismatch, it is possiblc to grow more CaF2 in a structure and a number of models have been proposed layer-by-layer rnodc wilhoul introducing strain relieving [1,2]. Despite this attention no consistent picture has dislocations. Using this 'template' method emerged. Conflicting results have been attributed to pseudomorphic growth tias been achieved up to a differences in sample preparation and the varying thickness of -60 TL's. Smplcs were capped with 50A sensitivity of experimental techniques [3,4,5]. The of amorphous Si and rcrnovcd from the vacuum for TEM problem relates to more general issues concerning the and x-ray diffracljon mcasurcmcnts. differences between surface and interface structure. In particular, it is questionable whether the structure Experimental Details and Results observed at monolayer coverages, which is accessible to many standard surface probes, is representative of the X-ray reflectivity is a powerful technique for true interface between two materials 161. The latter can determining surfacc struckm and has been employed only be studied with techniques that employ highly with considerable succcss in studies of reconsuucted penetrating beams, such as x-ray diffraction and metal surfaces [8.9]. The technique is analogous to transmission elcctron microscopy (TEM). It is the LEED or RHEED measurements of the (0 0) specular structure of the buried interface that influences the rod, but the weak interaction of x-rays with matter electronic properties. enables use of the kincrnatical approximation to The aim of our program is to combine x-ray scattering theory, in the form of a one-dimensional diffraction and TEM to study the CaFzjSi(ll1) interface. Fourier summation over the layers of the crystal [lo]. The samples are grown by molecular beam epitaxy Figure 1 shows the reflectivity profile for a 7TL thick (MBE), enabling strict control of the growth conditions. CaF2 film. The measurement was performed on beam This combination of state-of-the art technologies offers a line 7-2 at the Stanford Synchrotron Radiation unique opportunity to study the relatively unexplored Laboratory using a 4-circle Huber diffractomeler and a phenomena of phase transitions and reconstructions at focussed lmm (vertical x 2mm (horizontal) incident x- buried interfaces. ray beam (h = 1.2398d ). The sample was mounted at the center of the diffractometer axes, with its surface Sample Preparation normal in the vertical scattering plane. Scattered x-rays were detected by a scintillation counter after passing CaF2 was grown by MBE on well-oriented through 6mm (vertical) x lOmm (horizontal) slits at a (misc~t<0.5~)Si (1 11) substrates in an ISA/Riber CBE distance of -1m from the sample. Each point 32P ultrahigh vacuum (UHV) system. The Shiraki corresponds to a background subtracted integrated etched Si substrates [7] were outgassed thoroughly and intensity obtaincd from 9 scans at the appropriate 29 then heated to 880°C to remove the protective oxide. scattering angle along the specular rod. Thc data has Cooling to the growth tcmpcrature (720°C) routinely bccn corrected for the Lorentz factor (sin 28) and the resulted in a sharp (7x7) reflection high-cncrgy elcctron variation of samplc arca illuminatcd by the x-ray beam diffraction (RHEED) pattern. CaF2 was deposited by (sin 9). No dam was collected for LcO.9 rcciprocal evaporation from an effusion cell at 1150°C. During lattice units duc to scattering from the amorphous Si cap deposition the pressure was typically -1~10-~Otorr at a which affccts thc low angle reflectivity data. The 108 0023248: intensity diverges at the Si (111) Bragg reflection and was not measured over the range G-.98-1.02 Si( 11 1) 0 reciprocal lauice units (Si r.1.u.). F(q) = fsi(q) C exp(iqzj) j=-- ' 100 N + exp(iqd) { fca(q)+2fsos(qc/4))C exp(iqzk) h ._.dvl 10 k=O e 7 fSi(q) , f&(q) and fF(s> are atomic form factors which include the Debye-Waller factor [13], zj are the atomic height coordinates, c is the lattice spacing of the CaF2 film with a thickness of N mple layers, and d is the interface separation. Although the model fits the data around the (1 11) Bragg reflection it is clearly not a good fit to the data over the larger q range. Between Bragg reflections the scattering from atoms in bulk positions 0.01 I I I interferes destructively and is roughly equal in intensity 1 .o 1.5 2.0 2.5 u) the scattering from an isolated monolayer [14]. The (0 0 L) recip. latt. units measurement is thus sensitive to the details of the interface structure projected onto the surface normal Figure 1. Measured x-ray reflectivity of a 7 uiple direction. An isolated monolayer at the interface is layer (TL) CaF2/Si(lll) film. The data points are simple to include in the scattering model with an background subtracted integrated intensities corrected for additional multiplying factor pj representing a possible the Lorentz factor and the variation in illuminated partial layer occupation (i.e. pj varies between 0 and 1). sample area. The dashed line is a calculation with a Swain in t'te interface region can be accounted for by simple interface model (interface spacing d=4.55A). The allowing the bulk layers to move away from their ideal solid line is a fit to the data with a two-layer interface positions. There are a number of constraints which according to the parameters in Table I. must be imposcd on the modelling procedure: we look for a model which has physically reasonable bondlengths In a recent paper we presented similar x-ray scattering and is consistent with previous results. It has been measurements from CaFdSi(l1 l), over a reduced range shown that upon initial adsorption the CaF2 molecule of L (0.8-1.2) around the Si (1 11) Bragg reflection [I 11. dissociates to give a sub-monolayer coverage of CaF The measurement is sensitive LO the "long-range" [ 1.4.51. We can reproduce our data by including a CaF interface separation from the bulk of the substrate to the layer at the interface but this results in a Si-Ca bulk of the film [ 121. Over this L range good fits to the separation of -1.6A which is not compatible with the data were obtained with a lattice separation d = 4.55A. Ca-Si bondlength (3.0-3.2A) [15]. The best fit to the This value indicates that there is a layer in between the data with a two-layer interface (the next simplest model) two lattices. The dashed line in Figure 1 corresponds to is shown by the solid line in Figure 1.
Load more

Recommended publications
  • ASB M B Annual Meeting Highlights from the 2009
    2010 ANNUAL MEETING, APRIL 24-28. ANAHEIM AWAITS! hlights fr ig om H June 2009 t h e 2 0 0 9 A S B M B A n n u al Meeting American Society for Biochemistry and Molecular Biology ANNUAL REVIEWS A Nonprofit Scientific Publisher INSIGHTFUL ANNUAL REVIEW OF TABLE OF CONTENTS BIOCHEMISTRY Without a License, or Accidents Waiting to Happen, E. Peter Geiduschek RESEARCH IN • A Journey in the World of DNA Rings and Beyond, James C. Wang BIOCHEMISTRY Vol. 78 • JUlY 2009 • The Biochemistry of Disease: Desperately Seeking Syzygy, John W. Kozarich • Biosynthesis of Phosphonic and Phosphinic Acid Natural STARTS WITH Editor: Products, William W. Metcalf, Wilfred A. van der Donk • New Antivirals and Drug Resistance, Peter M. Colman • Multidrug Resistance in Bacteria, Roger D. Kornberg ANNUAL Hiroshi Nikaido • Conformational Pathology of the Serpins: Themes, REVIEWS Stanford University School Variations, and Therapeutic Strategies, Bibek Gooptu, David A. Lomas of Medicine • Getting a Grip on Prions: Oligomers, Amyloids, and Pathological Membrane Interactions, Byron Caughey, Gerald S. Baron, Bruce Chesebro, Annual Review of Martin Jeffrey • RING Domain E3 Ubiquitin Ligases, Raymond J. Deshaies, Biochemistry, in publication Claudio A.P. Joazeiro • Regulation and Cellular Roles of Ubiquitin- since 1932, sets the standard Specific Deubiquitinating Enzymes, Francisca E. Reyes-Turcu, Karen H. Ventii, Keith D. Wilkinson • Recognition and Processing of Ubiquitin- for review articles in biological Protein Conjugates by the Proteasome, Daniel Finley • Degradation of chemistry and molecular biology. Activated Protein Kinases by Ubiquitination, Zhimin Lu, Tony Hunter • The Since its inception, these volumes Role of Ubiquitin in the NFκB Regulatory Pathways, Brian Skaug, Xiaomo have served as an indispensable Jiang, Zhijian J.
    [Show full text]
  • Martian Crater Morphology
    ANALYSIS OF THE DEPTH-DIAMETER RELATIONSHIP OF MARTIAN CRATERS A Capstone Experience Thesis Presented by Jared Howenstine Completion Date: May 2006 Approved By: Professor M. Darby Dyar, Astronomy Professor Christopher Condit, Geology Professor Judith Young, Astronomy Abstract Title: Analysis of the Depth-Diameter Relationship of Martian Craters Author: Jared Howenstine, Astronomy Approved By: Judith Young, Astronomy Approved By: M. Darby Dyar, Astronomy Approved By: Christopher Condit, Geology CE Type: Departmental Honors Project Using a gridded version of maritan topography with the computer program Gridview, this project studied the depth-diameter relationship of martian impact craters. The work encompasses 361 profiles of impacts with diameters larger than 15 kilometers and is a continuation of work that was started at the Lunar and Planetary Institute in Houston, Texas under the guidance of Dr. Walter S. Keifer. Using the most ‘pristine,’ or deepest craters in the data a depth-diameter relationship was determined: d = 0.610D 0.327 , where d is the depth of the crater and D is the diameter of the crater, both in kilometers. This relationship can then be used to estimate the theoretical depth of any impact radius, and therefore can be used to estimate the pristine shape of the crater. With a depth-diameter ratio for a particular crater, the measured depth can then be compared to this theoretical value and an estimate of the amount of material within the crater, or fill, can then be calculated. The data includes 140 named impact craters, 3 basins, and 218 other impacts. The named data encompasses all named impact structures of greater than 100 kilometers in diameter.
    [Show full text]
  • The History of Valentine Camp by Mary Farrell
    History of Valentine Camp Mary M. Farrell Trans-Sierran Archaeological Research P.O. Box 840 Lone Pine, CA 93545 November 7, 2015 Prepared for Valentine Eastern Sierra Reserve University of California, Santa Barbara, Natural Reserve System Sierra Nevada Aquatic Research Laboratory 1016 Mt. Morrison Road Mammoth Lakes, CA 93546 Abstract Located in Mammoth Lakes, California, Valentine Camp and the nearby Sierra Nevada Aquatic Research Laboratory form the Valentine Eastern Sierra Reserve, a field research station in the University of California's Natural Reserve System. The University’s tenure at Valentine Camp began over 40 years ago, but the area’s history goes back thousands of years. Before the arrival of Euroamericans in the nineteenth century, the region was home to Paiutes and other Native American tribes. Land just east of Valentine Camp was surveyed under contract with the United States government in 1856, and mineral deposits in the mountains just west of Valentine Camp brought hundreds of miners to the vicinity in the last decades of the nineteenth century. Even as mining in the region waned, grazing increased. The land that became Valentine Camp was patented in 1897 by Thomas Williams, a rancher and capitalist who lived in Owens Valley. It was Williams’s son, also Thomas, who sold the 160 acres to Valentine Camp’s founders. Those founders were very wealthy, very influential men in southern California who could have, and did, vacation wherever they wanted. Anyone familiar with the natural beauty of Mammoth Lakes would not be surprised that they chose to spend time at Valentine Camp. Valentine Camp was donated to the University of California Natural Land and Water Reserve System (now the Natural Reserve System) in 1972 to ensure the land’s continued protection.
    [Show full text]
  • Assessing Mimicry of the Transition State
    View Article Online / Journal Homepage / Table of Contents for this issue PERSPECTIVE www.rsc.org/obc | Organic & Biomolecular Chemistry Glycosidase inhibition: assessing mimicry of the transition state Tracey M. Gloster*a,b and Gideon J. Davies*a Received 5th August 2009, Accepted 30th September 2009 First published as an Advance Article on the web 5th November 2009 DOI: 10.1039/b915870g Glycoside hydrolases, the enzymes responsible for hydrolysis of the glycosidic bond in di-, oligo- and polysaccharides, and glycoconjugates, are ubiquitous in Nature and fundamental to existence. The extreme stability of the glycosidic bond has meant these enzymes have evolved into highly proficient catalysts, with an estimated 1017 fold rate enhancement over the uncatalysed reaction. Such rate enhancements mean that enzymes bind the substrate at the transition state with extraordinary affinity; the dissociation constant for the transition state is predicted to be 10-22 M. Inhibition of glycoside hydrolases has widespread application in the treatment of viral infections, such as influenza and HIV, lysosomal storage disorders, cancer and diabetes. If inhibitors are designed to mimic the transition state, it should be possible to harness some of the transition state affinity, resulting in highly potent and specific drugs. Here we examine a number of glycosidase inhibitors which have been developed over the past half century, either by Nature or synthetically by man. A number of criteria have been proposed to ascertain which of these inhibitors are true transition state mimics, but these features have only be critically investigated in a very few cases. Introduction molecules, lipids or proteins), constitute between 1 and 3% of the genome of most organisms.1 The task facing these enzymes Glycosidases, the enzymes responsible for the breakdown of di-, with respect to maintaining efficient and highly specific catalysis oligo- and polysaccharides, and glyconjugates, are ubiquitous is no mean feat; it has been calculated that there are 1.05 ¥ 1012 through all kingdoms of life.
    [Show full text]
  • Bioactive Nanotherapeutic Trends to Combat Triple Negative Breast Cancer
    University of Texas Rio Grande Valley ScholarWorks @ UTRGV School of Medicine Publications and Presentations School of Medicine 3-13-2021 Bioactive nanotherapeutic trends to combat triple negative breast cancer Pallabita Chowdhury University of Tennessee Health Science Center Upasana Ghosh Kamalika Samanta Meena Jaggi The University of Texas Rio Grande Valley, [email protected] Subhash C. Chauhan The University of Texas Rio Grande Valley, [email protected] See next page for additional authors Follow this and additional works at: https://scholarworks.utrgv.edu/som_pub Part of the Chemicals and Drugs Commons Recommended Citation Chowdhury, P., Ghosh, U., Samanta, K., Jaggi, M., Chauhan, S. C., & Yallapu, M. M. (2021). Bioactive nanotherapeutic trends to combat triple negative breast cancer. Bioactive materials, 6(10), 3269–3287. https://doi.org/10.1016/j.bioactmat.2021.02.037 This Article is brought to you for free and open access by the School of Medicine at ScholarWorks @ UTRGV. It has been accepted for inclusion in School of Medicine Publications and Presentations by an authorized administrator of ScholarWorks @ UTRGV. For more information, please contact [email protected], [email protected]. Authors Pallabita Chowdhury, Upasana Ghosh, Kamalika Samanta, Meena Jaggi, Subhash C. Chauhan, and Murali M. Yallapu This article is available at ScholarWorks @ UTRGV: https://scholarworks.utrgv.edu/som_pub/324 Bioactive Materials 6 (2021) 3269–3287 Contents lists available at ScienceDirect Bioactive Materials journal homepage: www.sciencedirect.com/journal/bioactive-materials Bioactive nanotherapeutic trends to combat triple negative breast cancer Pallabita Chowdhury a, Upasana Ghosh b, Kamalika Samanta a, Meena Jaggi a,c,d, Subhash C.
    [Show full text]
  • Obituary 1967
    OBITUARY INDEX 1967 You can search by clicking on the binoculars on the adobe toolbar or by Pressing Shift-Control-F Request Form LAST NAME FIRST NAME DATE PAGE # Abbate Barbara F. 6/6/1967 p.1 Abbott William W. 9/22/1967 p.30 Abel Dean 11/27/1967 p.24 Abel Francis E. 9/25/1967 p.24 Abel Francis E. 9/27/1967 p.10 Abel Frederick B. 11/11/1967 p.26 Abel John Hawk 12/7/1967 p.42 Abel John Hawk 12/11/1967 p.26 Abel William E. 7/10/1967 p.28 Abel William E. 7/12/1967 p.12 Aber George W. 3/14/1967 p.24 Abert Esther F. 7/26/1967 p.14 Abrams Laura R. Hoffman 8/14/1967 p.28 Abrams Laura R. Hoffman 8/17/1967 p.28 Abrams Pearl E. 10/19/1967 p.28 Abrams Pearl E. 10/20/1967 p.10 Achenbach Helen S. 11/6/1967 p.36 Achenbach Helen S. 11/8/1967 p.15 Ackerman Calvin 5/22/1967 p.34 Ackerman Calvin 5/25/1967 p.38 Ackerman Fritz 11/27/1967 p.24 Ackerman Harold 10/27/1967 p.26 Ackerman Harold 10/28/1967 p.26 Ackerman Hattie Mann 4/14/1967 p.21 Ackerman Hattie Mann 4/19/1967 p.14 Adamczyk Bennie 5/3/1967 p.14 Adamo Margaret M. 3/15/1967 p.15 Adamo Margaret M. 3/20/1967 p.28 Adams Anna 6/17/1967 p.22 Adams Anna 6/20/1967 p.17 Adams Harriet C.
    [Show full text]
  • Oxidative Stress, a New Hallmark in the Pathophysiology of Lafora Progressive Myoclonus Epilepsy Carlos Romá-Mateo *, Carmen Ag
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Digital.CSIC 1 Oxidative stress, a new hallmark in the pathophysiology of Lafora progressive myoclonus epilepsy Carlos Romá-Mateo1,2*, Carmen Aguado3,4*, José Luis García-Giménez1,2,3*, Erwin 3,4 3,5 1,2,3# Knecht , Pascual Sanz , Federico V. Pallardó 1 FIHCUV-INCLIVA. Valencia. Spain 2 Dept. Physiology. School of Medicine and Dentistry. University of Valencia. Valencia. Spain 3 CIBERER. Centro de Investigación Biomédica en Red de Enfermedades Raras. Valencia. Spain. 4 Centro de Investigación Príncipe Felipe. Valencia. Spain. 5 IBV-CSIC. Instituto de Biomedicina de Valencia. Consejo Superior de Investigaciones Científicas. Valencia. Spain. * These authors contributed equally to this work # Corresponding author: Dr. Federico V. Pallardó Dept. Physiology, School of Medicine and Dentistry, University of Valencia. E46010-Valencia, Spain. Fax. +34963864642 [email protected] 2 ABSTRACT Lafora Disease (LD, OMIM 254780, ORPHA501) is a devastating neurodegenerative disorder characterized by the presence of glycogen-like intracellular inclusions called Lafora bodies and caused, in most cases, by mutations in either EPM2A or EPM2B genes, encoding respectively laforin, a phosphatase with dual specificity that is involved in the dephosphorylation of glycogen, and malin, an E3-ubiquitin ligase involved in the polyubiquitination of proteins related with glycogen metabolism. Thus, it has been reported that laforin and malin form a functional complex that acts as a key regulator of glycogen metabolism and that also plays a crucial role in protein homeostasis (proteostasis). In relationship with this last function, it has been shown that cells are more sensitive to ER-stress and show defects in proteasome and autophagy activities in the absence of a functional laforin-malin complex.
    [Show full text]
  • The Metabolism of Tay-Sachs Ganglioside: Catabolic Studies with Lysosomal Enzymes from Normal and Tay-Sachs Brain Tissue
    The Metabolism of Tay-Sachs Ganglioside: Catabolic Studies with Lysosomal Enzymes from Normal and Tay-Sachs Brain Tissue JOHN F. TALLMAN, WILLIAM G. JOHNSON, and ROSCOE 0. BRADY From the Developmental and Metabolic Neurology Branch, National Institute of Neurological Diseases and Stroke, National Institutes of Health, Bethesda, Maryland 20014, and the Department of Biochemistry, Georgetown University School of Medicine, Washington, D. C. 20007 A B S T R A C T The catabolism of Tay-Sachs ganglioside, date fronm the 19th century and over 599 cases have been N-acetylgalactosaminyl- (N-acetylneuraminosyl) -galac- reported (1). Onset of the disease is in the first 6 months tosylglucosylceramide, has been studied in lysosomal of life and is characterized by apathy, hyperacusis, motor preparations from normal human brain and brain ob- weakness, and appearance of a macular cherry-red spot tained at biopsy from Tay-Sachs patients. Utilizing Tay- in the retina. Seizures and progressive mental deteriora- Sachs ganglioside labeled with '4C in the N-acetylgalac- tion follow with blindness, deafness, and spasticity, lead- tosaminyl portion or 3H in the N-acetylneuraminosyl ing to a state of decerebrate rigidity. These infants usu- portion, the catabolism of Tay-Sachs ganglioside may be ally die by 3 yr of age (2). initiated by either the removal of the molecule of A change in the chemical composition of the brain of N-acetylgalactosamine or N-acetylneuraminic acid. The such patients was first detected by Klenk who showed activity of the N-acetylgalactosamine-cleaving enzyme that there was an increase in the ganglioside content (hexosaminidase) is drastically diminished in such compared with normal human brain tissue (3).
    [Show full text]
  • Pages 459 To
    459 University Organization Board of Trustees The dean of the Heller School for Social study abroad, international students and Policy and Management oversees the scholars, and student enrichment services), academic activities of the school and its Hiatt Career Center, research and planning, Under Massachusetts law, the Board of work in such policy areas as children, and student life (including athletics, Trustees is the governing body of the youth, families, health, mental health, chaplaincy, community service, health university. There are four faculty substance abuse, disabilities, aging, social services, intercultural center, judicial representatives and three student change, and economic inequalities. orientation, psychological counseling, representatives to the board who participate residence life, and student activities). in board meetings and have votes on the The dean of the Brandeis International several committees. The president of the Business School oversees the academic, The senior vice president for university, the chair of the Fellows, the professional, and development activities communications administers and executes president of the Brandeis National of the university’s second professional critical university-wide internal and Committee, and the president of the school. Research areas of the school external communications, overseeing the Alumni Association serve ex officio. The include economic policy, finance, global communications emergency response plan board annually elects an alumni term entrepreneurship, international business, and directing all crisis communications. trustee who serves a four-year term with regional economics integration, and trade Further, she is responsible for an integrated full voting privileges. and exports. marketing communications program that highlights Brandeis’s research The President accomplishments, academic excellence, The president, the chief executive officer of The Faculty Senate social justice mission, and scholarly the university, is appointed by the Board of contributions to the Jewish community.
    [Show full text]
  • Ithaca Classified Business Directory 1935
    JAMIESON - McKINNEY COMPANY HOME HUMIDIFYING SYSTEMS AND HOT WATER 115-121 S. CAYUGA ST. PHONE 3434 1935-ITHAcA DIRECTORY-1935 379 MANNING'S Ithaca Classified Business Directory 1935 Copyright 1935, by H. A. Manning Co. *Indicates heading given by special arrangement with publishers *ABDOMINAL SUPPORTERS (BRANDS) FAHEY EMPLOYMENT AGENCY, 124 E PARADOX, AB Brooks & Son, 126 E State, State, see p 66 see p 67 Student Agencies (Inc), 409 College av ACCOUNTANTS AND AUDITORS Boynton Leland C, 1006 EState AGRICULTURAL IMPLEMENTS MAXFIELD TERRELL B, Savings Bank Anderson & Eddy Implement Co, 107 E bldg (219), see p 60 Green LANG JB ENGINE & GARAGE CO, 117 E *ACCOUNTING SCHOOLS Green, see p 43 (See Business Colleges) AIR BRUSH (PHOTOGRAPHY) *ACETYLENE WELDING FRANZ STUDIO THE, 214 E State, see p 80 CARL'S GARAGE, 201 E Tompkins, see back cover AIR CONDITIONING LANG'S PALACE GARAGE, 117-133 E JAMIESON-McKINNEY CO, 115-121 S Green, see p 43 Cayuga, see top margins REYNOLDS & DRAKE GARAGE CO, 216 S Cayuga, see front cover and p 45 AIRPORTS ADVERTISING AGENCIES Ithaca Flying Service, Taughannock blvd Agricultural Advertising and Research Ser­ Ithaca Municipal Airport, Taughannock blvd vice, 110 N Tioga Ithaca Sales & Pedigree Co, 513 N Tioga ALCOHOLIC BEVERAGE CONTRAl BUREAUS Roberts Grace E, 316 N Aurora Tompkins County Alcoholic Control Board 202 EState (601) *ADVERTISING SIGNS (See Sign Painters and Manufacturers) *ALUMINUM AND ENAMEL WARE AGENCIES ROTHSCHILD BROS, 155-59 E State and CO-OPERATIVE GLF EXCHANGE INC, 100-26 S Tioga, see p 7 Seneca bldg, 112 E Seneca RUMSEY CJ & CO, 206 E State, see p 64 CAREY BLDG.
    [Show full text]
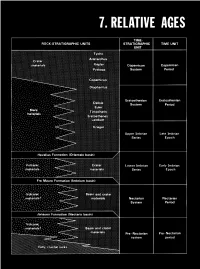
  • Relative Ages
    CONTENTS Page Introduction ...................................................... 123 Stratigraphic nomenclature ........................................ 123 Superpositions ................................................... 125 Mare-crater relations .......................................... 125 Crater-crater relations .......................................... 127 Basin-crater relations .......................................... 127 Mapping conventions .......................................... 127 Crater dating .................................................... 129 General principles ............................................. 129 Size-frequency relations ........................................ 129 Morphology of large craters .................................... 129 Morphology of small craters, by Newell J. Fask .................. 131 D, method .................................................... 133 Summary ........................................................ 133 table 7.1). The first three of these sequences, which are older than INTRODUCTION the visible mare materials, are also dominated internally by the The goals of both terrestrial and lunar stratigraphy are to inte- deposits of basins. The fourth (youngest) sequence consists of mare grate geologic units into a stratigraphic column applicable over the and crater materials. This chapter explains the general methods of whole planet and to calibrate this column with absolute ages. The stratigraphic analysis that are employed in the next six chapters first step in reconstructing
    [Show full text]
  • DMAAC – February 1973
    LUNAR TOPOGRAPHIC ORTHOPHOTOMAP (LTO) AND LUNAR ORTHOPHOTMAP (LO) SERIES (Published by DMATC) Lunar Topographic Orthophotmaps and Lunar Orthophotomaps Scale: 1:250,000 Projection: Transverse Mercator Sheet Size: 25.5”x 26.5” The Lunar Topographic Orthophotmaps and Lunar Orthophotomaps Series are the first comprehensive and continuous mapping to be accomplished from Apollo Mission 15-17 mapping photographs. This series is also the first major effort to apply recent advances in orthophotography to lunar mapping. Presently developed maps of this series were designed to support initial lunar scientific investigations primarily employing results of Apollo Mission 15-17 data. Individual maps of this series cover 4 degrees of lunar latitude and 5 degrees of lunar longitude consisting of 1/16 of the area of a 1:1,000,000 scale Lunar Astronautical Chart (LAC) (Section 4.2.1). Their apha-numeric identification (example – LTO38B1) consists of the designator LTO for topographic orthophoto editions or LO for orthophoto editions followed by the LAC number in which they fall, followed by an A, B, C or D designator defining the pertinent LAC quadrant and a 1, 2, 3, or 4 designator defining the specific sub-quadrant actually covered. The following designation (250) identifies the sheets as being at 1:250,000 scale. The LTO editions display 100-meter contours, 50-meter supplemental contours and spot elevations in a red overprint to the base, which is lithographed in black and white. LO editions are identical except that all relief information is omitted and selenographic graticule is restricted to border ticks, presenting an umencumbered view of lunar features imaged by the photographic base.
    [Show full text]