Line Stabbing Bounds in Three Dimensions Abstract 1 Introduction
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Official Form 309F (For Corporations Or Partnerships)
17-22445-rdd Doc 9 Filed 03/28/17 Entered 03/28/17 11:28:37 Ch 11 First Mtg Corp/Part Pg 1 of 3 Information to identify the case: Debtor Metro Newspaper Advertising Services, Inc. EIN 13−1038730 Name United States Bankruptcy Court Southern District of New York Date case filed for chapter 11 3/27/17 Case number: 17−22445−rdd Official Form 309F (For Corporations or Partnerships) Notice of Chapter 11 Bankruptcy Case 12/15 For the debtor listed above, a case has been filed under chapter 11 of the Bankruptcy Code. An order for relief has been entered. This notice has important information about the case for creditors, debtors, and trustees, including information about the meeting of creditors and deadlines. Read both pages carefully. The filing of the case imposed an automatic stay against most collection activities. This means that creditors generally may not take action to collect debts from the debtor or the debtor's property. For example, while the stay is in effect, creditors cannot sue, assert a deficiency, repossess property, or otherwise try to collect from the debtor. Creditors cannot demand repayment from the debtor by mail, phone, or otherwise. Creditors who violate the stay can be required to pay actual and punitive damages and attorney's fees. Confirmation of a chapter 11 plan may result in a discharge of debt. A creditor who wants to have a particular debt excepted from discharge may be required to file a complaint in the bankruptcy clerk's office within the deadline specified in this notice. -

642117 109.Pdf
17-22445-rdd Doc 109 Filed 10/04/17 Entered 10/04/17 13:27:05 Main Document Pg 1 of 99 17-22445-rdd Doc 109 Filed 10/04/17 Entered 10/04/17 13:27:05 Main Document Pg 2 of 99 Metro Newspaper17-22445-rdd Advertising Services, Doc Inc. 109 - U.S. MailFiled 10/04/17 Entered 10/04/17 13:27:05 Main DocumentServed 10/2/2017 Pg 3 of 99 1808 GREENSBORO MAGAZINE 21ST CENTURY MEDIA 22ND CENTURY MEDIA 200 E. MARKET STREET ATTN: CARA EVERETT 11516 W. 183RD PLACE GREENSBORO, NC 27401 12320 ORACLE BLVD STE 310 UNIT SW CONDO 3 COLORADO SPRINGS, CO 80921 ORLAND PARK, IL 60467 280 LIVING 360 WEST MAGAZINE ABERDEEN AMERICAN NEWS P.O. BOX 530341 1612 SUMMIT AVENUE SUITE 150 BOX 4430 BIRMINGHAM, AL 35253 FORT WORTH, TX 76102 124 S 2ND STREET ABERDEEN, SD 57402 ABERDEEN WORLD ABILENE REPORTER ABILENE REPORTER NEWS C/O SOUND PUBLISHING C/O GANNETT COMPANY /JMG SITES PO BOX 630849 11323 CAMMANDO RD W UNIT 651 N. BOONVILLE AVE CINCINNATI, OH 45263 EVERETT, WA 98204 SPRINGFIELD, MO 65806 ABILENE REPORTER NEWS - ACCOUNT #804426 ABINGTON/AVON ARGUS SENTINEL ABOUT TOWN ATTN: KATHLEEN HENNESSEY 26 WEST SIDE SQUARE ATTN: HUNT GILLESPIE 7950 JONES BRANCH DR. MACOMB, IL 61455 PO BOX 130328 MCLEAN, VA 22107 BIRMINGHAM, AL 35213 ABOUT TOWN ABOUT TOWN GILLESPIE INC ACADIANIA COMMUNITY ADVOCATE GILLESPIE INC HUNT GILLESPIE 10705 RIEGER RD P.O. BOX 130328 PO BOX 130328 BATON ROUGE, LA 70810 BIRMINGHAM, AL 35213 BIRMINGHAM AL 35213 ADA EVENING NEWS ADAMS TIMES REPORTER ADCRAFT ROSTER EDITION 116 NORTH BROADWAY 116 S MAIN C/O ADCRAFT CLUB OF DETROIT ADA, OK 74820 P.O. -

On the Number of Minimal 1-Steiner Trees
On the Number of Minimal 1-Steiner Trees Boris Aronov Marshall Bern† David Eppstein‡ Abstract We count the number of nonisomorphic geometric minimum spanning trees formed by adding a single point to an n-point set in d-dimensional space, by relating it to a family of 2 convex decompositions of space. The O(nd log2d d n) bound that we obtain signicantly improves previously known bounds and is tight to within a polylogarithmic factor. The minimum Steiner tree of a point set is the tree of minimum total length, spanning the in- put points and possibly having some additional vertices. Georgakopoulos and Papadimitriou [1] dene the minimum 1-Steiner tree as the minimum spanning tree whose set of vertices consists of the input points and exactly one extra point. They describe an algorithm for constructing this tree in the plane by enumerating all combinatorially distinct minimal 1-Steiner trees, that is, trees formed by xing the position of the extra vertex and considering the minimum span- ning tree of the resulting set of points. They give an O(n2) bound on the number of such trees and construct a matching lower bound. Independently, Monma and Suri [3] proved the same bounds in the plane and gave bounds of O(n2d) and (nd) in any dimension d. We signicantly improve Monma and Suri’s upper bounds. We show that the maximum possible number of 2 combinatorially distinct minimal 1-Steiner trees on n points in d-space is O(nd log2d d n) for all dimensions d. Our bounds require—as do the bounds in previous papers—either an assump- tion of general position or a tie-breaking rule, so that the minimum spanning tree is unique; otherwise even in the plane there can be exponentially many distinct topologies. -

Firefighter Informational Tutorial
The careerof a lifetime starts here. Carlos F. Munroe Sarina Olmo AnitaDaniel Danny Chan Brooke Guinan AndrewM. Brown Battalion 35 Ladder29 Engine234 Ladder109 Engine312 Ladder176 FIREFIGHTER INFORMATIONAL TUTORIAL [PAGE INTENTIONALLY LEFT BLANK] Daniel A. Nigro Fire Commissioner July 5, 2017 Dear Applicants, This test preparation guide has been assembled to help prepare you for the upcoming New York City Firefighter exam, and was developed to complement the online tutorial that you'll find on the DCAS website (nyc.gov). This booklet will provide you with valuable test and note-taking tips, along with sample math and reading comprehension exercises. In addition, the new exam format includes video exercises which will help applicants judge how well they are taking notes, retaining information and answering questions. I want to thank the FDNY Recruitment & Retention team for preparing this booklet. I also want to thank each applicant for attending these sessions and taking advantage of the opportunity to learn as much as you can about the test. I began my career as a Firefighter in 1969, rising through all of the ranks, and now, as Fire Commissioner, I can tell you there is no better job in the world than being one of New York City's Bravest. I, therefore, encourage you to study and work hard in preparation for the upcoming test. I wish each and every one of you good luck on the test! Daniel A. Nigro Fire Commissioner DAN/yk Fire Department, City of New York 9 MetroTech Center Brooklyn New York 11201-3857 TABLE OF CONTENTS SUGGESTED READING COMPREHENSION TIPS ....................................................................................................... -

The Pacific Park Brooklyn Project Is the Redevelopment of 22 Acres In
CREDIT VUW PACIFIC PARK BROOKLYN The Pacific Park Brooklyn project is the redevelopment of 22 acres in downtown Brooklyn that will include approximately 6 million square feet of residential space (6,430 units of affordable and market-rate housing), a state of the art sports and entertainment arena, the Barclays Center, 247,000 square feet of retail use, approximately 336,000 square feet of office space and 8 acres of publicly accessible open space. The project plan permits a program variation which could allow for up to 1.6 million square feet of commercial space. The project also includes major transportation improvements, including a new storage and maintenance facility for the LIRR and a new subway entrance to the Atlantic Terminal Transit Hub, the third largest hub in the City. Atlantic Yards’ Master Plan was designed by Frank Gehry. The development was renamed Pacific Park Brooklyn in July, 2014. DEVELOPER In 2006 New York State approved Forest City Ratner Companies’ master plan for Atlantic Yards. In June of 2014, Greenland, USA and Forest City Ratner Companies closed on a joint venture agreement to develop all phases of the project – excluding Barclays Center and the first residential tower, 461 Dean Street, already under construction – including infrastructure, a permanent MTA rail yard, a platform above the rail yard, future residential units and future commercial high-rise development. Greenland Forest City Partners was chosen as the name of the new development company. SCHEDULE In June of 2014, Greenland Forest City Partners, New York State and New York City reached a deal to accelerate the build-out of Pacific Park Brooklyn. -
Emergency Response Incidents
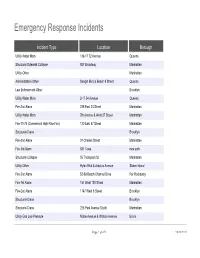
Emergency Response Incidents Incident Type Location Borough Utility-Water Main 136-17 72 Avenue Queens Structural-Sidewalk Collapse 927 Broadway Manhattan Utility-Other Manhattan Administration-Other Seagirt Blvd & Beach 9 Street Queens Law Enforcement-Other Brooklyn Utility-Water Main 2-17 54 Avenue Queens Fire-2nd Alarm 238 East 24 Street Manhattan Utility-Water Main 7th Avenue & West 27 Street Manhattan Fire-10-76 (Commercial High Rise Fire) 130 East 57 Street Manhattan Structural-Crane Brooklyn Fire-2nd Alarm 24 Charles Street Manhattan Fire-3rd Alarm 581 3 ave new york Structural-Collapse 55 Thompson St Manhattan Utility-Other Hylan Blvd & Arbutus Avenue Staten Island Fire-2nd Alarm 53-09 Beach Channel Drive Far Rockaway Fire-1st Alarm 151 West 100 Street Manhattan Fire-2nd Alarm 1747 West 6 Street Brooklyn Structural-Crane Brooklyn Structural-Crane 225 Park Avenue South Manhattan Utility-Gas Low Pressure Noble Avenue & Watson Avenue Bronx Page 1 of 478 09/30/2021 Emergency Response Incidents Creation Date Closed Date Latitude Longitude 01/16/2017 01:13:38 PM 40.71400364095638 -73.82998933154158 10/29/2016 12:13:31 PM 40.71442154062271 -74.00607638041981 11/22/2016 08:53:17 AM 11/14/2016 03:53:54 PM 40.71400364095638 -73.82998933154158 10/29/2016 05:35:28 PM 12/02/2016 04:40:13 PM 40.71400364095638 -73.82998933154158 11/25/2016 04:06:09 AM 40.71442154062271 -74.00607638041981 12/03/2016 04:17:30 AM 40.71442154062271 -74.00607638041981 11/26/2016 05:45:43 AM 11/18/2016 01:12:51 PM 12/14/2016 10:26:17 PM 40.71442154062271 -74.00607638041981 -

Newly Wed Checklist (Active and Retired)
SECURITY BENEFIT FUND OF THE UNIFORMED FIREFIGHTERS ASSOCIATION OF GREATER NEW YORK LOCAL 94 I.A.F.F. AFL-CIO 204 EAST 23rd STREET, NEW YORK, N.Y. 10010 TEL: (212) 683-4723 • FAX: (212) 683-0693 Follow us on Twitter @ufanyc Facebook @ufanyc Instagram @ufa94nyc Web Address: www.ufanyc.org SBF/Beneficiary Enrollment Form Submission: www.ufanycbenefits.org Email: [email protected] NEWLY WED CHECKLIST (ACTIVE & RETIRED) To add your spouse to your: YOU MUST: 1. City Health Plan ACTIVE MEMBERS: THE PREFERRED METHOD for ACTIVE MEMBERS (to notify FDNY HQ and add a spouse to your medical coverage) is to go online WITHIN 30 DAYS to the NYCAPS / Employee Please note that if you have Self Service (ESS) program at www.nyc.gov/ess. MARRIED your DOMESTIC Alternatively, you can fill out and forward a Health Benefit Application (also known as an ERB Form) PARTNER, you should also with a copy of your Marriage Certificate to add your spouse to your medical plan, to: REVIEW the Domestic Partner BUREAU OF PERSONNEL RESOURCES / HEALTH PLAN UNIT checklist!! Your Marriage 9 METROTECH CENTER, 6th FL, BROOKLYN, NY 11201-5431 Certificate should *also* be sent PHONE 718-999-2196 FAX 718-999-7139 email [email protected] to OLR (see the Retiree section). During COVID Closures, for best results, add spouse using NYCAPS/ESS, and *also* email the ERB Make sure you include your form *and* Marriage Certificate to Noreen Aspromonte at [email protected]. FULL SS# and a way you **Click here to go to the Health Benefit Application/ERB Form.** can be reached when RETIREES: Must fill out a Health Benefit Application or ERB Form (CLICK HERE for the sending to OLR. -

1 Metrotech Center Brooklyn, NY Newly Renovated Office Space Available
1 Metrotech Center Brooklyn, NY Newly Renovated Office Space Available • Partial 11th Floor: 18,250 RSF • Available January, 2020 • 5-7 year Term • Rent Available Upon Request • Located in the Brooklyn Tech Triangle, 10 minutes to Manhattan, with excellent access to Public Transportation (A,C,B,F,G N,R,1 train stops) • Close proximity to the Brooklyn Marriott and 75+ restaurants Shawna Menifee +1 212 915 7256 [email protected] Jones Lang LaSalle Brokerage, Inc. | 330 Madison Avenue New York, NY 10017 DISCLAIMER Although information has been obtained from sources deemed reliable, neither Owner nor JLL makes any guarantees, warranties or representations, express or implied, as to the completeness or accuracy as to the information contained herein. Any projections, opinions, assumptions or estimates used are for example only. There may be differences between projected and actual results, and those differences may be material. The Property may be withdrawn without notice. Neither Owner nor JLL accepts any liability for any loss or damage suffered by any party resulting from reliance on this information. If the recipient of this information has signed a confidentiality agreement regarding this matter, this information is subject to the terms of that agreement. ©2019 Jones Lang LaSalle IP, Inc. All rights reserved. Unit B Features: • 26 private windowedoffices • Open space for 60-80 personalworkstations • Fully equipped kitchen with seating for 25-30 people 1 Metrotech Center • 2 ADA compliant privatebathrooms Partial 11th Floor E • Great light and exposures with windows on 3sides Unit B 18,250 SF N S Jones Lang LaSalle Brokerage, Inc. -

990-PF Or Section 4947(A)(1) Trust Treated As Private Foundation | Do Not Enter Social Security Numbers on This Form As It May Be Made Public
**PUBLIC DISCLOSURE COPY** Return of Private Foundation OMB No. 1545-0047 Form 990-PF or Section 4947(a)(1) Trust Treated as Private Foundation | Do not enter social security numbers on this form as it may be made public. Department of the Treasury 2019 Internal Revenue Service | Go to www.irs.gov/Form990PF for instructions and the latest information. Open to Public Inspection For calendar year 2019 or tax year beginning , and ending Name of foundation A Employer identification number THE NATHAN CUMMINGS FOUNDATION, INC. 23-7093201 Number and street (or P.O. box number if mail is not delivered to street address) Room/suite B Telephone number 475 TENTH AVENUE, 14TH FLOOR 212-787-7300 City or town, state or province, country, and ZIP or foreign postal code C If exemption application is pending, check here ~ | NEW YORK, NY 10018 G Check all that apply: Initial return Initial return of a former public charity D 1. Foreign organizations, check here ~~ | Final return Amended return 2. Foreign organizations meeting the 85% test, Address change Name change check here and attach computation ~~~~ | X H Check type of organization: Section 501(c)(3) exempt private foundation E If private foundation status was terminated Section 4947(a)(1) nonexempt charitable trust Other taxable private foundation under section 507(b)(1)(A), check here ~ | X I Fair market value of all assets at end of yearJ Accounting method: Cash Accrual F If the foundation is in a 60-month termination (from Part II, col. (c), line 16) Other (specify) under section 507(b)(1)(B), check here ~ | | $ 444,315,012. -

Fire Department 9 Metrotech Center Brooklyn, N.Y
FIRE DEPARTMENT 9 METROTECH CENTER BROOKLYN, N.Y. 11201-3857 BUREAU OF FIRE PREVENTION Public Buildings Unit DATE: 07.30.2020. PREMISES HEBREWYeshiva Machzikei LANGUAGE Hadas ACADEMY HEBREW LANGUAGE ACADEMY 2186 Mill Avenue 2186 Mill Avenue Brooklyn, NY 11234 Brooklyn, NY 11234 To Whom It May Concern: The New York City Fire Department (“FDNY”), Bureau of Fire Prevention, Public Buildings Unit conducted an inspection of the above-referenced premises on 07.28.2020. XXX The inspection did not reveal any violations that FDNY’s Public Buildings Unit is authorized to inspect and enforce. The inspection resulted in issuance of violations of the Fire Code or other laws, rules or regulations that FDNY’s Public Buildings Unit is authorized to inspect and enforce. As of 11/12/2019 Documents were submitted to FDNY as proof of correction, and such correction was deemed acceptable to FDNY The inspection, and a review of premises records, has disclosed that the premises may not be in compliance with the lawful occupancy established by the New York City Department of Buildings. This letter shall not be construed to be a permit for, or an approval of the premises. FDNY does not certify that the premises is free from any violation for which it has not inspected, in accordance with its standard inspection protocols. This letter shall not prevent FDNY from inspecting the premises at a later date, requiring the correction of any deficiencies its finds at the premises, and/or issuing violations against the premises for conditions that do not comply with the Fire Code or other laws, rules or regulations. -

Catalog of Courses, Scholarships and Partner Colleges 2009 Catalog Of
Catalog of Courses, Scholarships and Partner Colleges 20092009 BUREAU OF TRAINING MESSAGE FROM THE MAYOR Dear Friends: I am pleased to introduce the 2009 Course Opportunities Catalog for the New York City Fire Department. FDNY’s uniformed and civilian workforce is the world’s best, and does so much to keep all New Yorkers safe. In fact, civilian fire fatalities remained at historically low levels in fiscal year 2008. This incredible achievement is no accident: no one is better prepared than our Bravest. Whether you’ve been in the Department for 20 days — or for 20 years — the training never ends. I know that this catalog will be a terrific resource as you continue that tradition by learning new skills that will contribute to your personal growth and the Department’s continued success. On behalf of all New Yorkers, thank you for your incredible dedication, service and sacrifice for our great City. Sincerely, Michael R. Bloomberg Mayor B UREAU OF T RAINING i MESSAGE FROM THE FIRE COMMISSIONER n my seven years as Commissioner of this great Department, I have made training a top prior- ity. From developing with Columbia University a high level management training course for Isenior officers, to nearly doubling the amount of training provided to probationary firefighters, the Department has done a great deal to address through improved training the many public safety challenges we face in today’s changing world. The key to a successful Department is a well-trained, highly motivated professional staff. The men and woman who wear the FDNY and Emergency Medical Service uniforms are out in the streets every day helping New Yorkers in need. -

PA/ID 1-2011 EMS OGP 113-08 December 27, 2011 WORKPLACE
PA/ID 1-2011 EMS OGP 113-08 December 27, 2011 WORKPLACE VIOLENCE PREVENTION POLICY 1. POLICY STATEMENT 1.1 The New York City Fire Department promulgates this policy to prevent and minimize instances of violence in the workplace between Department employees and all persons who they come in contact with in the course of conducting their assigned tasks. This policy is also promulgated to encourage employees to report all instances of, and concerns regarding, physical violence (assaults and homicides), attempted assaults, threats reasonably perceived to result in physical violence, or other conduct that would be reasonably expected to lead to an assault or a homicide, to ensure that those reports are reviewed on an expedited basis, and, where appropriate, to ensure that de-escalation and/or corrective measures are taken. 1.2 The Fire Department is responsible for evaluating its workplace, determining factors and situations that may place employees at risk of workplace violence, developing and implementing a written prevention program, and providing employees with information and training on the risks of workplace violence. 1.3 To this end, the Fire Department, with the participation and input of management, employees, and authorized employee representatives, has conducted a risk evaluation of the agency’s operations and facilities, and has identified risk factors for workplace violence that are present and the workplace violence control measures that minimize the risk of workplace violence, and has prepared this policy. Participation by employees and employee representatives is an important part of our program. The written program will be reviewed on an annual basis. The Fire Department will continue to solicit feedback from authorized employee representatives on the program, annual review of facilities, and annual review of trends in workplace violence prevention trends at least annually.