DOCSLIB.ORG

NROSCI/BIOSC 1070 and MSNBIO 2070 September 27, 2017

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
NROSCI/BIOSC 1070 and MSNBIO 2070 September 27, 2017 NROSCI/BIOSC 1070 and MSNBIO 2070 September 27, 2017 Cardiovascular 6 Special Circulations Coronary Muscle The coronary arteries branch directly from the aorta, and provide the perfusion of the heart. Although blood actually is pumped through the heart, only ~ 100 µm of the inner endocardial surface can obtain significant amounts of nutrition directly from the blood supply in the cardiac chambers. Blood flow through the coronary capillaries during systole and diastole is different than in most other tissues of the body. The blood flow to the ventricles falls during systole, and increases during diastole. During ventricular contrac- tion, blood flow through the capillaries is obstructed by compression of the vessels. Thus, blood flow increases during diastole when the muscle around the vessels relaxes. Autoregulatory mechanisms are paramount in adjusting the blood flow through the heart. Another major influence on dilation of the coronary arteries is epinephrine released from the adrenal gland. Cerebral Circulation The cerebral circulation is almost completely insensitive to neural and hormonal influences that produce vasoconstriction elsewhere in the body. By far the predominant factor that controls blood flow through the cerebral circulation is paracrine release. In particular, carbon dioxide has a strong vasodilation effect on the cerebral vessels. Skeletal Muscle Circulation Control of blood flow to skeletal muscle is in many respects similar to that in the heart. Paracrine fac- tors have strong influences, and vasodilation is induced by the release of epinephrine from the adrenal gland. A major difference between the two circulations is that skeletal muscle arterioles are richly in- nervated by sympathetic vasoconstrictor fibers, and are major resistance vessels to contribute to total peripheral resistance. Because skeletal muscle mass is so large, vasodilation of muscle vessels would greatly diminish total peripheral resistance unless vasoconstriction occurs in other vascular beds. It is thus necessary that the central nervous system provides control of blood flow through skeletal muscle. 9/27/17 Page 1 Cardiovascular 6 Body Fluid Compartments: Fluid in the body is located in three distinct compartments: Plasma (~ 3 L) Interstitial fluid (~12 L) Intracellular fluid (~25 L) To reach that intracellular compartment from the plasma, a molecule must diffuse across the capillary plasma membrane into the interstitial compartment, and then across the cell membrane into the intracellular fluid. Capillaries are composed of a single layer of endothelial cells and a basement mem- brane; the thickness of the wall is only about 0.5 micrometers. Small intercellular clefts typically separate the endothelial cells. Capillaries are often associated with elongated, highly branched cells that form a meshlike layer between the endothelium and interstitial fluid. These cells are called pericytes. The pericytes contribute to restricting capillary permeability. Exchange of materials through capillaries usually occurs through diffusion. Small and uncharged and lipid-soluble molecules (including O2 and CO2) have no problem passing through the capillary wall. Larger and charged molecules may pass through the intercellular clefts or via vesicular transport. Water crosses the capillary through both in- tercellular channels and specialized water channels (aquaporins) in the endothelial cell membrane. In general, large molecules have a very difficult time escaping from capillaries, as shown in the table to the left. There are some exceptions, however. Some capillaries have receptors for particular proteins; once the protein binds it is carried across the membrane via a process called transcytosis. 9/27/17 Page 2 Cardiovascular 6 However, in some organs, very large proteins (and even cellular elements) need to enter or leave the circulation. Thus, some capillaries are fenestrat- ed (or have large pores) to facilitate this exchange. For example, the intestine contains fenestrated capil- laries so that large molecules can be moved from the GI tract to the bloodstream. In other organs (e.g., bone marrow and the spleen), the endothelial cells are discontinuous to permit red blood cells to enter the circulation. Osmotic Relationships Between Compartments Osmolarity is a measure of the absolute concentration of osmotically active particles. A solution of one mole/liter of non-dissociable solute is equivalent to 1 osmole/liter (1 Osm). Normal osmolarity of body fluids is about 300 mOsm. The osmotic pressure of a 1 Osm solution is 22.4 Atm, or 22.4 x 760 = 17,024 mmHg. Thus a 300 mOsm solution has an osmotic pressure equivalent of 17,024 x 0.3 = 5,107 mmHg. The only molecular species for which there is a significant concentration difference between the plasma and interstitial fluid is protein. All of the other solutes, which make up the major component of plasma osmolarity (Na+, Cl-, HCO3-), are present in approximately equivalent concentrations on both sides of the capillary membrane. Hence differences in protein concentration provide the only osmotic driving force at the capillary level. The plasma protein concentration is about 7 gm/100 cc plasma (7 gm%). The osmotic pressure generated by this protein is known as the oncotic pressure and is in the range of 25-28 mmHg. The oncotic pressure difference between the capillary plasma and the interstitial fluid tends to draw fluid INTO the capillary. However, another major force is at play in capillaries: hydrostatic pressure, which is due to the pressure in the blood imparted primarily by the contraction of the ventricle. The hydrostatic pressure is higher in the capillary than in the interstitial fluid, and tends to force fluid OUT of the capillary. The balance between oncotic pressure and hydrostatic pressure across the capillary will determine whether there is a net gain or loss of fluid across the vessel. This balance can be expressed quantita- tively via Starling’s equation (from the same Starling who formulated “Starling’s Law of the Heart.”) 9/27/17 Page 3 Cardiovascular 6 The Starling equation reads as follows: Jv = Kf ([Pc—Pi] — s [pc—pi]) Where: Pc = Capillary hydrostatic pressure Pi = Interstitial hydrostatic pressure pc = Capillary oncotic pressure pi = Interstitial oncotic pressure Kf = Filtration coefficient s = Reflection coefficient Jv = Net fluid movement between compartments In essence the equation says that the net filtration (Jv) is proportional to the net driving force. By con- vention, outward force is defined as positive, and inward force is defined as negative. Ifv J is positive, fluid will tend to leave the capillary (filtration). If Jv is negative, fluid will tend to enter the capillary (absorption). This equation has a number of important physiologic implications, especially when pathologic processes grossly alter one or more of the variables. The first four variables in the list above (Pc, Pi, pc, pi ) are the forces that contribute to the net driving force. The filtration coefficient f(K ) is the constant of proportionality. A high Kf value indicates a highly wa- ter permeable capillary. A low value indicates a low capillary permeability. The filtration coefficient is the product of two components: capillary surface area and capillary hydraulic conductance. The val- ues for both of these components are usually relatively high, and are fixed for a vascular bed, but there are exceptions. As you will learn during the renal section, the number of aquaporin channels inserted into the distal convoluted tubule and collecting ducts of the kidney nephrons is dependent on the levels of circulating vasopressin. In the absence of vasopressin, few aquaporins are present and Kf is low. The reflection coefficient (s) is often thought of as a correction factor. The idea is that the difference in oncotic pressures contributes to the net driving force because most capillaries in the body are fairly impermeable to the large molecular weight proteins. In fact, some smaller proteins can leak across the capillary membrane through the intercellular clefts, which must be accounted for as it diminishes the driving force. The reflection coefficient (s) is used to ‘correct for’ the ineffectiveness of some of the oncotic pressure gradient. It can have a value from 0 up to 1. Non-fenestrated vessels have a reflection coefficient close to 1, whereas the value is lower for fenestrated capillaries. Across a particular capillary, Kf and s are usually constant. As such, when we are considering the dynamics in a particular vascular bed, Starling’s equation can be restated as: Jv ≈ ([Pc—Pi] — [pc—pi]) Let’s consider a situation where the blood entering the arterial end of a capillary has a hydrostatic pressure of 25 mmHg, and also carries an oncotic pressure of 25 mmHg. In the adjacent interstitial space, hydrostatic pressure is usually slightly negative (approximately -3 mm Hg). Let’s also assume that interstital oncotic pressure is 5 mm Hg. In this case, Jv ≈ ([25 — (-3)] — [25 — 5]), or 8 mmHg. Since Jv is positive, fluid will tend to leave the capillary and filtration will occur. 9/27/17 Page 4 Cardiovascular 6 As blood passes along a capillary, it loses hydrostatic pressure due to friction. At the venule end, hy- drostatic pressure is often near 10 mmHg, If there has been no appreciable shift in protein balance be- tween the capillary and interstitial compartments, the relative oncotic pressures won’t change. Thus, at the venule end of the capillary, Jv ≈ ([10 — (-3)] — [25 — 5]), or -7 mmHg. Since Jv is negative, fluid will tend to enter the capillary and absorption will occur. Note that there is an imbalance in filtration and ab- sorption (8 mmHg of filtration at the arterial end and 7 mmHg of absorption at the venule end). As such, the net filtration pressure is 1 mmHg. In general, we tend to lose 2-4 liters of fluid per day into the interstitial space due to the filtration-absorption imbalance. The process is illustrated in the figure to the left. Luckily, the excess fluid lost into the interstitial space is collected by the lymphatic system, as de- scribed below.
Load more

Recommended publications
  • 24. the Endothelial Glycocalyx (C Alphonsus)
    Part I Anaesthesia Refresher Course – 2018 24 University of Cape Town The Endothelial Glycocalyx Dr Christella Alphonsus Dept of Anaesthesia & Perioperative Medicine University of Cape Town Overview The glycocalyx is a complex gel layer that coats all healthy vascular endothelium. This layer exists in dynamic interaction between flowing blood and the endothelial cell wall. It plays a pivotal role in vascular protection, modulation and haemostasis. Components The endothelial glycocalyx is essentially made up of glycoproteins or proteoglycans but there is great diversity in structure and function within these two groups. Proteoglycans have a protein core to which are attached negatively charged glycosaminoglycan (GAG) side chains. There are different types of proteoglycans and they vary according to: the core protein size, the number of GAG side chains and whether they are bound or not bound to the cell membrane. Syndecans and glypicans are first bound to the cell membrane and the GAG side chains are attached later. Other proteoglycans (perlecans, versicans, decorins, biglycans, mimecans) are first bound to GAGs and then secreted by the endothelial cells. There are five types of GAG side chains: heparan sulphate makes up 50–90%, with the remainder composed of hyaluronic acid and chondroiton, dermatan and keratin sulphates. Hyaluronic acid is the only GAG not usually bound to a core protein and forms viscous solutions with water. Glycoproteins act as adhesion molecules and contribute to the coagulation, fibrinolytic and haemostatic systems. These include E and P selectin which are expressed after stimulation by histamine, thrombin, interleukin-1 and tumour necrosis factora (TNF-α). Ligands for leucocyte and platelet adhesion ICAM-1, ICAM-2, VCAM-1, PECAM-1 are also expressed within the glycocalyx.
    [Show full text]
  • Application of Negative Tissue Interstitial Pressure Improves Functional Capillary Density After Hemorrhagic Shock in the Absence of Volume Resuscitation
    UC San Diego UC San Diego Previously Published Works Title Application of negative tissue interstitial pressure improves functional capillary density after hemorrhagic shock in the absence of volume resuscitation. Permalink https://escholarship.org/uc/item/3pc6m5m7 Journal Physiological reports, 9(5) ISSN 2051-817X Authors Jani, Vinay P Jani, Vivek P Munoz, Carlos J et al. Publication Date 2021-03-01 DOI 10.14814/phy2.14783 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Received: 21 January 2021 | Accepted: 5 February 2021 DOI: 10.14814/phy2.14783 ORIGINAL ARTICLE Application of negative tissue interstitial pressure improves functional capillary density after hemorrhagic shock in the absence of volume resuscitation Vinay P. Jani1 | Vivek P. Jani2 | Carlos J. Munoz1 | Krianthan Govender1 | Alexander T. Williams1 | Pedro Cabrales1 1Department of Bioengineering, University of California, San Diego, La Abstract Jolla, CA, USA Microvascular fluid exchange is primarily dependent on Starling forces and both the ac- 2 Division of Cardiology, Department of tive and passive myogenic response of arterioles and post-capillary venules. Arterioles Medicine, The Johns Hopkins University, The Johns Hopkins School of Medicine are classically considered resistance vessels, while venules are considered capacitance Baltimore, MD, USA vessels with high distensibility and low tonic sympathetic stimulation at rest. However, few studies have investigated the effects of modulating interstitial hydrostatic pressure, Correspondence Pedro Cabrales, University of particularly in the context of hemorrhagic shock. The objective of this study was to in- California, San Diego Department of vestigate the mechanics of arterioles and functional capillary density (FCD) during appli- Bioengineering, 0412 9500 Gilman cation of negative tissue interstitial pressure after 40% total blood volume hemorrhagic Dr.
    [Show full text]
  • Open Thesis.Pdf
    The Pennsylvania State University The Graduate School College of Engineering ROLE OF HEMODYNAMIC FORCES IN SMOOTH MUSCLE CELL CONTRACTION AND TRANSVASCULAR FILTRATION IN VIVO A Thesis in Bioengineering by Min-ho Kim © 2004 Min-ho Kim Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy December 2004 The thesis of Min-ho Kim was reviewed and approved* by the following: Norman R. Harris Associate Professor of Bioengineering Thesis Advisor Chair of Committee Herbert H. Lipowsky Professor of Bioengineering Peter J. Butler Assistant Professor of Bioengineering Donna H. Korzick Assistant Professor of Physiology and Kinesiology John M. Tarbell Distinguished Professor of Biomedical Engineering City College of New York / CUNY Special Member Herbert H. Lipowsky Professor of Bioengineering Head of the Department of Bioengineering *Signatures are on file in the Graduate School iii ABSTRACT The vascular wall is continuously exposed to two hemodynamic forces imparted by blood flow: pressure and shear stress. Significant changes in hemodynamic forces can occur in many physiological and pathophysiological circumstances. Changes in vascular pressure and blood flow-induced shear stress can affect vascular endothelium and smooth muscle cells (SMCs) mechanically. When vascular pressure is increased, an increase in transvascular filtration is driven by a classical Starling mechanism. This increased transvascular filtration is expected to induce increases in shear stresses through the inter- endothelial cleft surfaces and SMCs. A main hypothesis of the current study is that transvascular filtration-induced shear stress might play important roles in endothelial barrier function and SMC contractions. To address this hypothesis, we investigated the effect of pressure-induced transvascular fluid flux on SMC contraction in vivo.
    [Show full text]
  • 3 Physical Properties of the Body Fluids and the Cell Membrane
    Physical Properties 3 of the Body Fluids and the Cell Membrane 3.1 BODY FluIDS To begin our study of transport phenomena in biomedical engineering, we must first examine the physical properties of the fluids within the human body. Many of our engineering calculations and the development and design of new procedures, devices, and treatments will either involve or affect the fluids within the human body. Therefore, we will focus our initial attention on the types and characteristics of the fluids that reside within the body. Body fluids can be classified into three types: extracellular, intracellular, and transcellular fluids. As shown in Table 3.1, nearly 60% of the body weight for an average 70 kg male is composed of these body fluids, resulting in a total fluid volume of about 40 L. The largest fraction of the fluid volume, about 36% of the body weight, consists of intracellular fluid, which is the fluid contained within the body’s cells, e.g., the fluid found within red blood cells, muscle cells, and liver cells. Extracellular fluid consists of the interstitial fluid that comprises about 17% of the body weight and the blood plasma that comprises around 4% of the body weight. Interstitial fluid circulates within the spaces interstitium( ) between cells. The interstitial fluid space represents about one-sixth of the body volume. The interstitial fluid is formed as a filtrate from the plasma within the capillaries. The capillaries are the smallest element of the cardiovascular system and represent the site where the exchange of vital substances occurs between the blood and the tissue surround- ing the capillary.
    [Show full text]
  • Endothelial Glycocalyx and the Revised Starling Principle
    Learners’ Corner Perspective Endothelial Glycocalyx and the Revised Starling Principle contains a steep solute concentration gradient Edward S. Crockett due to its thickness and diffusion resistance.7 To summarize, hydrostatic and oncotic pres- Pharmacology, Center for Lung Biology College of Medicine sure gradients between the microvessel lumen University of South Alabama and the interstitium are dependent on the Mobile, Alabama eGCX. United States The importance for us research scientists is not the revision itself, but the idea that the eGCX holds the power to change our understanding Introduction of a fundamental principle for which much of It is not often a textbook paradigm that has our current knowledge on edema and vascu- withstood time for 100 years is put to the test. lar health is based. Since the presence of the In 1894, E. H. Starling found discrepancies in eGCX has not been considered in other physio- data presented by Heidenhain that suggested logical studies, unexplained phenomena could “lymph was to be looked upon as a secretion be attributed to eGCX function. rather than a transudation.”1 Starling was unable to reproduce many of Heidenhain’s Brief History of eGCX discovery experimental data and realized that lymph On the path to discovering the eGCX, two filtration was not an active process of secre- developments occurred that eventually merged tion. Instead, as we learn from any physiology and led to the revised Starling Principle: textbook, it is the equilibrium between hydro- (1) The invention of the electron microscope; 2 static and oncotic pressures. However, though and (2) Continued research on fluid exchange this is not completely wrong, it is incomplete.
    [Show full text]
  • Pulmonary Oedema: a Review
    PULMONARY OEDEMA: A REVIEW WILLIAM H. NOBLE ABSTRACT Pulmonary oedema results from derangement of a normal physiological process which is continuously producing and removing extravascular lung water according to principles stated by Starling's equation of fluid flow across semipermeable membranes. The parameters in Starling's equation cannot all be measured. However, experiments have suggested that increased pulmonary capillary hydrostatic pressure forces fluid extravascularly, diluting the colloid osmotic pressure of tissue fluids and increasing the hydrostatic pressure of lung tissue fluids. Once these reserves and the ability of puhnonary lymphatics to remove lung water are overcome, pulmonary oedema results. This oedema can also result from reduced colloid osmotic pressure in the pulmonary capillaries and increased capillary permeability, even at low pulmonary capillary hydrostatic l~ressure. Perhaps because of the reserve created by colloid osmotic pressure of tissue fluids, hy- drostatic pressure of lung tissue fluids and lymphatic drainage, pulmonary oedema accumu- lates at a slow rate initially, and at a much more rapid rate in later stages of oedema development. The rate of oedema formation may also relate to damage to the lung created by interstitial oedema, which opens the barrier to a later stage of alveolar oedema. While lung compliance is reduced with each successive increase in oedema formation, increased shunting and hypoxaemia do not result until alveolar oedema is present, in normal lung. The diagnosis of pulmonary oedema is best made by searching for causes of oedema and by chest radiographs. The management of pulmonary oedema must begin with maintenance of oxygenation of blood. This can best be achieved by applying continuous positive pressure ventilation (CPPV).
    [Show full text]
  • Perioperative Fluid Management
    Ehab Farag · Andrea Kurz Editors Perioperative Fluid Management 123 Perioperative Fluid Management Ehab Farag • Andrea Kurz Editors Perioperative Fluid Management Editors Ehab Farag Andrea Kurz Professor of Anesthesiology Professor of Anesthesiology Cleveland Clinic Lerner College of Medicine Cleveland Clinic Lerner College of Medicine Director of Clinical Research Chairman of General Anesthesia Staff Anesthesiologist Cleveland Clinic General Anesthesia and Outcomes Research Cleveland Cleveland Clinic Ohio Cleveland USA Ohio USA ISBN 978-3-319-39139-7 ISBN 978-3-319-39141-0 (eBook) DOI 10.1007/978-3-319-39141-0 Library of Congress Control Number: 2016955238 © Springer International Publishing Switzerland 2016 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifi cally the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfi lms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specifi c statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made.
    [Show full text]
  • Effective Pulmonary Capillary Pressure
    Eur Respir J EDITORIAL 1988, 1, 297-301 Effective pulmonary capillary pressure F.A. Grimbert The adult respiratory distress syndrome (ARDS) is The capillary filtration rate (Qfc) is a function of the almost invariably accompanied by permeability pulmo­ hydrostatic (.1P) and oncotic (.17t) pressure gradients on nary oedema, usually appearing in the first few hours either side of the capillary wall, and of the capillary [1, 2]. The extent and therefore the seriousness of this filtration coefficient (Kfc) which is the product of the oedema is proportional to the filtration of fluid and exchange surface area and the coefficient of hydraulic proteins through the pulmonary vascular endothelium. conductivity. .1P is the difference between intra­ The extreme sensitivity of this filtration to variations of vascular and interstitial hydrostatic pressures. The capillary pressure should lead us to consider any intravascular pressure which intervenes in the filtration lowering, however small, of the latter as an essential process in West's zone 3 is the intracapiUary pressure treatment of permeability pulmonary oedema [3, 4]. [8], except perhaps in the case of microembolisation Permeability pulmonary oedema (resuhing from an [9]. As for interstitial pressure, it hardly varies, with increase in pulmonary capillary permeability), contrasts just a few exceptions (pulmonary oedema following with hydrostatic pulmonary oedema (resulting from an either a tracheal obstruction [10] or the re-expansion increase in hydrostatic pressure). The increase in cap­ of a collapsed lung). The variations of the term .1P illary permeability is difficult LO observe; we are there­ therefore depend almost wholly upon variations in fore led to define permeability pulmonary oedema as an capillary pressure.
    [Show full text]
  • Fluid Physiology
    Fluid Physiology Fluid Physiology: A Handbook for Anaesthesia and Critical Care Practice By Thomas Woodcock Fluid Physiology: A Handbook for Anaesthesia and Critical Care Practice By Thomas Woodcock This book first published 2019 Cambridge Scholars Publishing Lady Stephenson Library, Newcastle upon Tyne, NE6 2PA, UK British Library Cataloguing in Publication Data A catalogue record for this book is available from the British Library Copyright © 2019 by Thomas Woodcock All rights for this book reserved. No part of this book may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior permission of the copyright owner. ISBN (10): 1-5275-4031-6 ISBN (13): 978-1-5275-4031-6 CONTENTS Foreword by William W. Muir ........................................................... xii Preface ...............................................................................................xiv Chapter 1.............................................................................................. 1 Starling’s Fluid Physiology: Historic Perspective Chapter summary.................................................................................. 1 The original Starling principle ............................................................... 2 The science of Starling forces ................................................................ 3 Revising the Starling principle ............................................................... 6 Large pores
    [Show full text]
  • Pulmonary Edema: a Unifying Pathophysiological Formula
    ular D asc ise v as io e rd s a & C D f i o a Journal of l g a n n o r s u i s o J Tilman, J Cardiovasc Dis Diagn 2015, 3:3 ISSN: 2329-9517 Cardiovascular Diseases & Diagnosis DOI: 10.4172/2329-9517.1000194 Research Article Open Access Pulmonary Edema: A Unifying Pathophysiological Formula Vladimir Tilman* Sheba Medical Center at Tel Hashomer, Holon, Israel *Corresponding author: Vladimir Tilman, Sheba Medical Center at Tel Hashomer, Rehabilitation Hospital, Eilat 33 apt 4, Holon, 58370, Israel, Tel: 972-0547345525; E- mail: [email protected] Received date: February 9, 2015; Accepted date: March 30, 2015; Published date: April 2, 2015 Copyright: © 2015 Tilman V. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Abstract Pulmonary edema is a significant complication of a number of disease and conditions. Its main manifestation is the leakage of fluid from the pulmonary capillaries into the cavity of the alveoli through the alveolar-capillary membrane. This leads to a number of severe clinical manifestations and requires immediate treatment. The underlying mechanisms causing this complication include cardiogenic and noncardiogenic factors. A formula is proposed to attempt to unify the causes of pulmonary edema, reflecting the relationship of all factors involved in the process. The formula is simple and evident, and covers all the factors that cause or contribute to the development of pulmonary edema. It also explains the pathogenesis of cardiogenic and noncardiogenic pulmonary edema and their relationship.
    [Show full text]
  • Capillary Permeability
    MICROCIRCULATIONMICROCIRCULATION FUNCTIONAL ANATOMY Microcirculation is circulation of the blood through the smallest vessels of the body – arteriols, capillaries and venules. (20-50 µm) (>50 µm) (4 - 9 µm) The principal function of the microcirculation is to permit the transfer of substances (water, solutes, gases) between the vascular system and the tissues. STRUCTURE OF VESSEL WALL 1 The capillary wall is about 1 µm thick. 2 The total area of all the capillary walls in the body exceeds 500 m2. 3 The rate of blood flow in capillaries is 0.2 - 1 mm/s. 4 Transit time from arterial to venular end of a capillary is 1 - 2 seconds. ULTRASTRUCTURE OF CAPILLARY Basement membrane Endothelial cell Nucleus Vesicles 5-10 µm Fenestrationes or pores Intercellular cleft Lumen Endothelial cell MOVEMENT OF FLUID ACCROSS CAPILLARY WALL Effect of hydrostatic pressure filtration Effect of oncotic resorption pressure diffusion The diffusion, filtration and resorption of water across capillary wall occur through Intercellular clefts, pores and fenestrations. OSMOTIC PREASURE osmotic osmotic (oncotic) (oncotic) pressure pressure hydrost. pressure PRESSURE GRADIENTS ACROSS THE WALL OF CAPILLARY arteriole venule capillary Net filtration pressure: INTERSTITIAL SPACE Net filtration pressure: Pc-Pi = 36 mmHg P P c c Pc -Pi = 16 mmHg π c= 25 Net resorption pressure: Net resorption pressure: π c- π i = 25 mmHg π c- π i = 25 mmHg 37 filtration resorption 17 Pi = 1 πi ≈ 0 CAPILLARY HYDROSTATIC PRESSURE Pc = 37 - 17 mmHg INTERSTITIAL HYDROSTATIC PRESSURE Pi = 1 mmHg
    [Show full text]
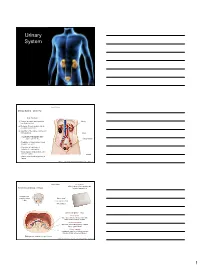
  • Urinary System
    Urinary System Urinary System Urinary System - Overview: Major Functions: 1) Removal of organic waste products Kidney from fluids (excretion) 2) Discharge of waste products into the environment (elimination) 1 3) Regulation of the volume / [solute] / pH 3 of blood plasma Ureter HOWEVER, THE KIDNEY AIN’T JUST FOR PEE’IN… Urinary bladder • Regulation of blood volume / blood pressure (e.g., renin) • Regulation of red blood cell formation (i.e., erythropoietin) 2 • Metabolization of vitamin D to active form (Ca++ uptake) Urethra • Gluconeogenesis during prolonged fasting Marieb & Hoehn (Human Anatomy and Physiology, 8th ed.) – Figure 25.1 Urinary System Renal ptosis: Kidneys drop to lower position due Functional Anatomy - Kidney: to loss of perirenal fat Located in the superior lumbar “Bar of soap” region 12 cm x 6 cm x 3 cm 150 g / kidney Layers of Supportive Tissue: Renal fascia: Peritoneal cavity Outer layer of dense fibrous connective tissue; anchors kidney in place Perirenal fat capsule: Fatty mass surrounding kidney; cushions kidney against blows Fibrous capsule: Transparent capsule on kidney; prevents infection of kidney from local tissues Kidneys are located retroperitoneal Marieb & Hoehn (Human Anatomy and Physiology, 8th ed.) – Figure 25.2 1 Urinary System Functional Anatomy - Kidney: Pyelonephritis: Inflammation of the kidney Pyramids appear striped due to parallel arrangement of capillaries / collecting tubes Renal cortex Renal medulla Renal pyramids Renal papilla Renal columns Renal hilum Renal pelvis • Entrance for blood vessels
    [Show full text]