DOCSLIB.ORG

Chapter 12: Lateral Earth Pressure

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 12: Lateral Earth Pressure Civil Engineering Department: Foundation Engineering (ECIV 4052) Part 4: Lateral Earth Pressure and Earth-Retaining Structures Chapter 12: Lateral Earth Pressure Introduction Vertical or near-vertical slopes of soil are supported by retaining walls, cantilever sheetpile walls, sheet-pile bulkheads, braced cuts, and other, similar structures. The proper design of those structures requires an estimation of lateral earth pressure, which is a function of several factors, such as: (a) the type and amount of wall movement, (b) the shear strength parameters of the soil, (c) the unit weight of the soil, and (d) the drainage conditions in the backfill. The following Figure shows a retaining wall of height H. For similar types of backfill: a. The wall may be restrained from moving (Figure a). The lateral earth pressure on the wall at any depth is called the at- rest earth pressure. b. The wall may tilt away from the soil that is retained (Figure b). With sufficient wall tilt, a triangular soil wedge behind the wall will fail. The lateral pressure for this condition is referred to as active earth pressure. c. The wall may be pushed into the soil that is retained (Figure c). With sufficient wall movement, a soil wedge will fail. The lateral pressure for this condition is referred to as passive earth pressure. Engr. Yasser M. Almadhoun Page 1 Civil Engineering Department: Foundation Engineering (ECIV 4052) Lateral Earth Pressure at Rest Consider a vertical wall of height H, as shown in Figure 12.3, retaining a soil having a unit weight of g. A uniformly distributed load, q/unit area, is also applied at the ground surface. At any depth z below the ground surface, the vertical subsurface stress is: If the wall is at rest and is not allowed to move at all, either away from the soil mass or into the soil mass (i.e., there is zero horizontal strain), the lateral pressure at a depth z is: Engr. Yasser M. Almadhoun Page 2 Civil Engineering Department: Foundation Engineering (ECIV 4052) For normally consolidated soil, the relation for Ko (Jaky, 1944) is: For overconsolidated soil, the at-rest earth pressure coefficient may be expressed as: The total force, Po, per unit length of the wall given in Figure 12.3a can now be obtained from the area of the pressure diagram given in Figure 12.3b and is: The location of the line of action of the resultant force, Po, can be obtained by taking the moment about the bottom of the wall. Thus: Engr. Yasser M. Almadhoun Page 3 Civil Engineering Department: Foundation Engineering (ECIV 4052) If the water table is located at a depth z, H, the at-rest pressure diagram shown in Figure 12.3b will have to be somewhat modified, as shown in Figure 12.4. If the effective unit weight of soil below the water table equals ’ (i.e., sat − w), then: Hence, the total force per unit length of the wall can be determined from the area of the pressure diagram. Specifically: So, Engr. Yasser M. Almadhoun Page 4 Civil Engineering Department: Foundation Engineering (ECIV 4052) Active Pressure Rankine Active Earth Pressure The Rankine active earth pressure calculations are based on the assumption that the wall is frictionless. The lateral earth pressure involves walls that do not yield at all. However, if a wall tends to move away from the soil a distance Δx, as shown in the following Figure, the soil pressure on the wall at any depth will decrease. For a wall that is frictionless, the horizontal stress, σ’h, at depth z will equal Koσ’o (=Koz) when Δx is zero. However, with Δx > 0, σ’h will be less than Koσ’o. Engr. Yasser M. Almadhoun Page 5 Civil Engineering Department: Foundation Engineering (ECIV 4052) Rankine active-pressure coefficient ∅′ 1 − sin ∅′ 퐾 = tan2 (45 − ) = 푎 2 1 + sin ∅′ The pressure distribution shows that at z = 0 the active pressure equals −2푐’√푘푎, indicating a tensile stress that decreases with depth and becomes zero at a depth z = zc, or: The depth zc is usually referred to as the depth of tensile crack, because the tensile stress in the soil will eventually cause a crack along the soil- wall interface. Thus, the total Rankine active force per unit length of the wall before the tensile crack occurs is: After the tensile crack appears, the force per unit length on the wall will be caused only by the pressure distribution between depths z = zc and z = H, as shown by the hatched area in the previous Figure. This force may be expressed as: Or: Engr. Yasser M. Almadhoun Page 6 Civil Engineering Department: Foundation Engineering (ECIV 4052) However, it is important to realize that the active earth pressure condition will be reached only if the wall is allowed to “yield” sufficiently. The necessary amount of outward displacement of the wall is as given as under: Wall movement for Soil type passive condition, Δx granular 0.001H − 0.004H cohesive .01H − 0.04H If there exists a surcharge load acting downward on the top surface of the backfill: The Rankine active stress at depth z can be calculated as follows: 휎ℎ(푎푐푡푣푒) = (푞 + 훾퐻)퐾푎 − 2푐√퐾푎 The Rankine active force per unit length of the wall at depth z can be calculated as follows: 1 푃 = (푞퐻 + 훾퐻2) 퐾 − 2푐√퐾 퐻 푎 2 푎 푎 Example 12.2 See example 2.2 in textbook, page 602. Example 12.3 See example 12.3 in textbook, page 604. Engr. Yasser M. Almadhoun Page 7 Civil Engineering Department: Foundation Engineering (ECIV 4052) A Generalized Case for Rankine Active Pressure – Granular Backfill In the previous section, the relationship was developed for Rankine active pressure for a retaining wall with a vertical back and a horizontal backfill. That can be extended to general cases of frictionless walls with inclined backs and inclined backfills. The previous Figure shows a retaining wall whose back is inclined at an angle with the vertical. The granular backfill is inclined at an angle α with the horizontal. The active force Pa for unit length of the wall then can be calculated as: Where Ka can be found from the Table 12.1 or using this equation: And the horizontal and vertical Rankine active forces (Pa(h) and Pa(v) respectively) for unit length of the wall is: 푃푎(ℎ) = 푃푎 cos(훽푎 + 휃) 푃푎(푣) = 푃푎 sin(훽푎 + 휃) Engr. Yasser M. Almadhoun Page 8 Civil Engineering Department: Foundation Engineering (ECIV 4052) Example 12.4 See example 12.4 in textbook, page 612. Granular Backfill with Vertical Back Face of Wall If the backfill of a frictionless retaining wall is a granular soil (c = 0) and rises at an angle α with respect to the horizontal, the active earth-pressure coefficient may be expressed in the form (or can be found from Table 12.3): At any depth z, the Rankine active pressure may be expressed as: Also, the total force per unit length of the wall is: Note that, in this case, the direction of the resultant force Pa is inclined at an angle α with the horizontal and intersects the wall at a distance H/3 from the base of the wall. Engr. Yasser M. Almadhoun Page 9 Civil Engineering Department: Foundation Engineering (ECIV 4052) Rankine Active Pressure with Vertical Wall Backface and Inclined c’- ϕ’ Soil Backfill For a frictionless retaining wall with a vertical back face ( = 0) and inclined backfill of c’− ϕ’ soil (see the following Figure) at an angle α with the horizontal, the active pressure at any depth z can be given as: where: Some values of K’a are given in Table 12.4. Engr. Yasser M. Almadhoun Page 10 Civil Engineering Department: Foundation Engineering (ECIV 4052) For a problem of this type, the depth of tensile crack is given as: Example 12.5 See example 12.5 in textbook, page 613. Coulomb’s Active Earth Pressure To apply Coulomb’s active earth pressure theory, let us consider a retaining wall with its back face inclined at an angle 훽 with the horizontal, as shown in Figure 12.12a. The backfill is a granular soil that slopes at an angle α with the horizontal. Also, let 훿′ be the angle of friction between the soil and the wall (i.e., the angle of wall friction). To find the active force, consider a possible soil failure wedge ABC1. The forces acting on this wedge (per unit length at right angles to the cross section shown) are as follows: 1. The weight of the wedge, W. Engr. Yasser M. Almadhoun Page 11 Civil Engineering Department: Foundation Engineering (ECIV 4052) 2. The resultant, R, of the normal and resisting shear forces along the surface, BC1. The force R will be inclined at an angle ϕ’ to the normal drawn to BC1. 3. The active force per unit length of the wall, Pa, which will be inclined at an angle 훿′ to the normal drawn to the back face of the wall. The maximum value of Pa thus determined is Coulomb’s active force (see top part of Figure 12.12a), which may be expressed as: where, Engr. Yasser M. Almadhoun Page 12 Civil Engineering Department: Foundation Engineering (ECIV 4052) The values of the active earth pressure coefficient, Ka, for a vertical retaining wall (훽 = 90°) with horizontal backfill (훼 = 0°) are given in Table 12.5. Note that the line of action of the resultant force (Pa) will act at a distance H/3 above the base of the wall and will be inclined at an angle 훿′ to the normal drawn to the back of the wall.
Load more

Recommended publications
  • Chapter Three Lateral Earth Pressure
    Addis Ababa University, Faculty of Technology, Department of Civil Engineering CHAPTER THREE LATERAL EARTH PRESSURE Table of Contents 3 Introduction ........................................................................................... 36 3.1 Definitions of Key Terms ....................................................................... 36 3.2 Lateral Earth Pressure at Rest ............................................................... 36 3.3 Active and Passive Lateral Earth Pressures .............................................. 38 3.4 Rankine Active and Passive Earth Pressures ............................................ 38 3.5 Lateral Earth Pressure due to Surcharge ................................................. 42 3.6 Lateral Earth Pressure When Groundwater is Present ................................ 43 3.7 Summary of Rankine Lateral Earth Pressure Theory ................................. 44 3.8 Rankine Active & Passive Earth Pressure for Inclined Granular Backfill ........ 45 3.9 Coulomb’s Earth Pressure Theory ........................................................... 46 Soil Mechanics II: Lecture Notes Instructor: Dr. Hadush Seged 35 Addis Ababa University, Faculty of Technology, Department of Civil Engineering 3 Introduction A retaining wall is a structure that is used to support a vertical or near vertical slopes of soil. The resulting horizontal stress from the soil on the wall is called lateral earth pressure . To determine the magnitude of the lateral earth pressure, a geotechnical engineer must know the basic soil
    [Show full text]
  • Seismic Lateral Earth Pressures on Retaining Structures
    Missouri University of Science and Technology Scholars' Mine International Conferences on Recent Advances 2010 - Fifth International Conference on Recent in Geotechnical Earthquake Engineering and Advances in Geotechnical Earthquake Soil Dynamics Engineering and Soil Dynamics 28 May 2010, 2:00 pm - 3:30 pm Seismic Lateral Earth Pressures on Retaining Structures A. Murali Krishna Indian Institute of Technology Guwahati, India Follow this and additional works at: https://scholarsmine.mst.edu/icrageesd Part of the Geotechnical Engineering Commons Recommended Citation Krishna, A. Murali, "Seismic Lateral Earth Pressures on Retaining Structures" (2010). International Conferences on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics. 13. https://scholarsmine.mst.edu/icrageesd/05icrageesd/session06/13 This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 4.0 License. This Article - Conference proceedings is brought to you for free and open access by Scholars' Mine. It has been accepted for inclusion in International Conferences on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics by an authorized administrator of Scholars' Mine. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. SEISMIC LATERAL EARTH PRESSURES ON RETAINING STRUCTURES A. Murali Krishna Indian Institute of Technology Guwahati Guwahati - India – 781039 ABSTRACT Various methods are available to estimate seismic earth pressures on soil retaining structures which cane be grouped to experimental, analytical and numerical methods. 1G model shaking table studies or high-g level centrifuge model shaking studies give some insight on the variation of seismic earth pressures along height of the retaining structure.
    [Show full text]
  • Geotechnical Design Manual Chapter 15- Retaining Structures
    VERSION 2.1 5/6/2019 GEOTECHNICAL DESIGN MANUAL CHAPTER 15- RETAINING STRUCTURES GEO-ENVIRONMENTAL SECTION OREGON DEPARTMENT OF TRANSPORTATION CHAPTER 15- RETAINING STRUCTURES TABLE OF CONTENTS SUMMARY OF CHANGES ............................................................................................................................... 6 15 RETAINING STRUCTURES .................................................................................................................. 7 15.1 INTRODUCTION ...........................................................................................................................................8 15.2 RETAINING WALL PRACTICES AND PROCEDURES ....................................................................................8 15.2.1 RETAINING WALL CATEGORIES AND DEFINITIONS ................................................................ 8 15.2.2 GENERAL STEPS IN A RETAINING WALL PROJECT ................................................................ 14 15.2.3 RETAINING WALL PROJECT SCHEDULE ................................................................................ 15 15.2.4 SELECTION OF RETAINING WALL SYSTEM TYPE ................................................................... 16 15.2.5 PROPRIETARY RETAINING WALL SYSTEMS .......................................................................... 19 15.2.6 NONPROPRIETARY RETAINING WALL SYSTEMS .................................................................. 19 15.2.7 UNIQUE NONPROPRIETARY WALL DESIGNS .......................................................................
    [Show full text]
  • Final Geotechnical Report Proposed Tower ‘B’ Multi-Level Building at the Corner of Parkdale Avenue and Bullman Street Ottawa, ON
    Final Geotechnical Report Proposed Tower ‘B’ Multi-Level Building at the Corner of Parkdale Avenue and Bullman Street Ottawa, ON Prepared for: Richcraft Group of Companies 2280 St. Laurent Blvd, Ottawa, ON K1G 4K1 Prepared by: Stantec Consulting Ltd. 1331 Clyde Ave, Ottawa, Ontario K2G 3H7 Project No. 122410780 June 2013 FINAL GEOTECHNICAL REPORT Table of Contents 1.0 INTRODUCTION ................................................................................................................ 1 2.0 SITE DESCRIPTION AND BACKGROUND ....................................................................... 1 3.0 SCOPE OF WORK ............................................................................................................. 1 4.0 METHOD OF INVESTIGATION .......................................................................................... 2 5.0 RESULTS OF INVESTIGATION ......................................................................................... 3 5.1 SUBSURFACE INFORMATION .......................................................................................... 3 5.1.1 Surficial Materials ................................................................................................. 3 5.1.2 Bedrock ................................................................................................................ 3 5.2 GROUNDWATER ............................................................................................................... 5 6.0 DISCUSSION AND RECOMMENDATIONS ......................................................................
    [Show full text]
  • Unit 3 Lateral Earth Pressure
    ANJUMAN COLLEGE OF ENGINEERING & TECHNOLOGY MANGALWARI BAZAAR ROAD, SADAR, NAGPUR - 440001. DEPARTMENT OF CIVIL ENGINEERING Geotechnical Engineering – II B.E. FIFTH SEMESTER Prof. Rashmi G. Bade, Department of Civil Engineering, Geotechnical Engineering – II 1 ANJUMAN COLLEGE OF ENGINEERING & TECHNOLOGY MANGALWARI BAZAAR ROAD, SADAR, NAGPUR - 440001. DEPARTMENT OF CIVIL ENGINEERING UNIT – III LATERAL EARTH PRESSURE: Earth pressure at rest, active & passive pressure, General & local states of plastic equilibrium in soil. Rankines and Coulomb‟s theories for earth pressure. Effects of surcharge, submergence. Rebhann‟s criteria for active earth pressure. Graphical construction by Poncelet and Culman for simple cases of wall-soil system for active pressure condition. Prof. Rashmi G. Bade, Department of Civil Engineering, Geotechnical Engineering – II 2 ANJUMAN COLLEGE OF ENGINEERING & TECHNOLOGY MANGALWARI BAZAAR ROAD, SADAR, NAGPUR - 440001. DEPARTMENT OF CIVIL ENGINEERING INTRODUCTION This is required in designs of various earth retaining structures like: - i) Retaining walls ii) Sheeting & bracings in cuts / excavations iii) Bulkheads iv) Bridge abutments, tunnels, cofferdams etc. Lateral earth pressure depends on:- i) Type of soil. ii) Type of wall movement:- a) Translatory b) Rotational iii) Soil-structure interaction. A retaining wall or retaining structure is used for maintaining the ground surface at different elevations on either side of it. The material retained or supported by the structure is called backfill which may have its top surface horizontal or inclined. The position of the backfill lying above a horizontal plane at the elevation of the top of a wall is called the surcharge, and its inclination to the horizontal is called surcharge angle β. Lateral earth pressure can be grouped into 3 categories, depending upon the movement of the retaining wall with respect to the soil retained.
    [Show full text]
  • Seismic Design of Earth Retaining Structures by Atop Lego, M.Tech (Struct.) SSW (E/Z) AP, PWD; Itanagar Introduction
    Seismic Design of Earth Retaining Structures By Atop Lego, M.Tech (Struct.) SSW (E/Z) AP, PWD; Itanagar Introduction The problem of retaining soil is one the oldest in the geotechnical engineering; some of the earliest and most fundamental principles of soil mechanics were developed to allow rational design of retaining walls. Many approaches to soil retention have been developed and used successfully. In the recent years, the development of metallic, polymer, and geotextile reinforcement has also led to the development of many innovative types of mechanically stabilized earth retention system. Retaining walls are often classified in terms of their relative mass, flexibility, and anchorage condition. The common types of the retaining wall are: 1. Gravity Retaining wall 2. Cantilever Retaining wall 3. Counter fort Retaining wall 4. Reinforced Soil Retaining wall 5. Anchored bulkhead a. Gravity b. Cantilever c. Reinforced soil Wall wall wall d. Anchored e. Counterfort Retaining bulkhead Fig. 1 Common type of Retaining Wall Gravity Retaining walls (Fig 1 a) are the oldest and simplest type of retaining walls. The gravity wall retaining walls are thick and stiff enough that they do not bend; their movement occurs essentially by rigid body translation and or by rotation. 2 The cantilever retaining wall as shown in Fig.1b bends as well as translates and rotates. They rely on the flexural strength to resist lateral earth pressures. The actual distribution of lateral earth pressure on a cantilever wall is influenced by the relative stiffness and deformation both the wall and the soil. In the present context considering the maximum applicability of free standing gravity retaining wall the presentation is focused mainly on the seismic design of gravity retaining wall.
    [Show full text]
  • Earth Pressure Theory and Application
    CHAPTER 4 EARTH PRESSURE THEORY AND APPLICATION EARTH PRESSURE THEORY AND APPLICATION 4.0 GENERAL All shoring systems shall be designed to withstand lateral earth pressure, water pressure and the effect of surcharge loads in accordance with the general principles and guidelines specified in this Caltrans Trenching and Shoring Manual. 4.1 SHORING TYPES Shoring systems are generally classified as unrestrained (non-gravity cantilevered), and restrained (braced or anchored). Unrestrained shoring systems rely on structural components of the wall partially embedded in the foundation material to mobilize passive resistance to lateral loads. Restrained shoring systems derive their capacity to resist lateral loads by their structural components being restrained by tension or compression elements connected to the vertical structural members of the shoring system and, additionally, by the partial embedment (if any) of their structural components into the foundation material. 4.1.1 Unrestrained Shoring Systems Unrestrained shoring systems (non-gravity cantilevered walls) are constructed of vertical structural members consisting of partially embedded soldier piles or continuous sheet piles. This type of system depends on the passive resistance of the foundation material and the moment resisting capacity of the vertical structural members for stability; therefore its maximum height is limited by the competence of the foundation material and the moment resisting capacity of the vertical structural members. The economical height of this type of wall is generally limited to a maximum of 18 feet. 4.1.2 Restrained Shoring Systems Restrained Shoring Systems are either anchored or braced walls. They are typically comprised of the same elements as unrestrained (non-gravity cantilevered) walls, but derive additional lateral resistance from one or more levels of braces, rakers, or anchors.
    [Show full text]
  • Internal Design of Mechanically Stabilized Earth (MSE) Retaining Walls Using Crimped Bars
    Utah State University DigitalCommons@USU All Graduate Theses and Dissertations Graduate Studies 5-2010 Internal Design of Mechanically Stabilized Earth (MSE) Retaining Walls Using Crimped Bars Bernardo A. Castellanos Utah State University Follow this and additional works at: https://digitalcommons.usu.edu/etd Part of the Civil Engineering Commons Recommended Citation Castellanos, Bernardo A., "Internal Design of Mechanically Stabilized Earth (MSE) Retaining Walls Using Crimped Bars" (2010). All Graduate Theses and Dissertations. 580. https://digitalcommons.usu.edu/etd/580 This Thesis is brought to you for free and open access by the Graduate Studies at DigitalCommons@USU. It has been accepted for inclusion in All Graduate Theses and Dissertations by an authorized administrator of DigitalCommons@USU. For more information, please contact [email protected]. INTERNAL DESIGN OF MECHANICALLY STABILIZED EARTH (MSE) RETAINING WALLS USING CRIMPED BARS by Bernardo A. Castellanos A thesis submitted in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE in Civil and Environmental Engineering Approved: _________________________ _________________________ James A. Bay John D. Rice Major Professor Committee Member _________________________ _________________________ Marvin W. Halling Byron R. Burnham Committee Member Dean of Graduate Studies UTAH STATE UNIVERSITY Logan, Utah 2010 ii ABSTRACT Internal Design of Mechanically Stabilized Earth (MSE) Retaining Walls Using Crimped Bars by Bernardo A. Castellanos, Master of Science Utah State University, 2010 Major Professor: Dr. James A. Bay Department: Civil and Environmental Engineering Current design codes of Mechanically Stabilized Earth (MSE) Walls allow the use lower lateral earth pressure coefficient (K value) for designing geosynthetics walls than those used to design steel walls.
    [Show full text]
  • Stability Assessment of Earth Retaining Structures Under Static and Seismic Conditions
    Article Stability Assessment of Earth Retaining Structures under Static and Seismic Conditions Sanjay Nimbalkar 1, Anindya Pain 2,*, Syed Mohd Ahmad 3 and Qingsheng Chen 4 1 School of Civil and Environmental Engineering, University of Technology Sydney, City Campus, NSW 2007, Australia; [email protected] 2 Geotechnical Engineering Group, CSIR-Central Building Research Institute, Roorkee-247667, India 3 University of Manchester, Oxford Rd, Manchester, M13 9PL, UK; [email protected] 4 School of Civil Engineering, Architecture and Environment, Hubei University of Technology, Wuhan 430068, China; [email protected] * Correspondence: [email protected] Received: 28 January 2019; Accepted: 30 March 2019; Published: 9 April 2019 Abstract: An accurate estimation of static and seismic earth pressures is extremely important in geotechnical design. The conventional Coulomb’s approach and Mononobe-Okabe’s approach have been widely used in engineering practice. However, the latter approach provides the linear distribution of seismic earth pressure behind a retaining wall in an approximate way. Therefore, the pseudo-dynamic method can be used to compute the distribution of seismic active earth pressure in a more realistic manner. The effect of wall and soil inertia must be considered for the design of a retaining wall under seismic conditions. The method proposed considers the propagation of shear and primary waves through the backfill soil and the retaining wall due to seismic excitation. The crude estimate of finding the approximate seismic acceleration makes the pseudo-static approach often unreliable to adopt in the stability assessment of retaining walls. The predictions of the active earth pressure using Coulomb theory are not consistent with the laboratory results to the development of arching in the backfill soil.
    [Show full text]
  • Field Measurements of Lateral Earth Pressures on a Cantilever
    TECHNICAL REPORT STANDARD TITLE PAGf 1. Rr•port No. 3. Recipient's Catalog No. 5. Report Date September 1973 FIELD MEASUREMENTS OF LATERAL EARTH PRESSURES ON A f--····· . -·-- --· -------·· PRE-CAST PANEL RETAINING WALL 6. Performing Organization Code . 7Dlvf~ 1 t( p~~~-~~tt~-H~rr~-M.--Coy·l~--_a_n_d_L_l_.o_n_e_l_J-.-- -~-Pe-rf~-,m-in·a--Or-ga-ni-za-,i-o,-R-e-po-,,-N-o_----1 Mi lberger Research Report No. 169-3 1-------·-- 9. Performing Organization Nam·o and Address 10. Work Unit No. Texas Transportation Institute Texas A&M University 11. Contract or Grant No. College Station, Texas 77843 13. Type ol Report and Period Covered 12.·-·s;;:;;~--rin_g_A-ge-nc_y_N-am_e_a-nd'-A-d-dr-.. s~-----------------~ Interim - Septernber 1970 Texas Highway Department Septetrber 1973 11th & Brazos 14. Sponsoring Agency-Code Austin, Texas 78701 15. SopplementoryNotes Research performedin cooperation with DOT, FHWA. Research Study Title: "Determination of Lateral Earth Pressure for Use in Retain­ ing Wall Design. 11 16. Ab a tract Terra Tee penumatic earth pressure cells are used to measure lateral earth pressures acting on a pre-cast panel retaining wall. Force transducers are used between the panel and the supporting structural members to measure the total force exerted on the panel by the backfill material. Accurate measurements of panel movements are made during and after backfilling. Data are presented for measured pressures, forces, and movements covering a period of 65 days. Physical and engineering properties of the backfill material are determined. Reasonably good correlation between the forces calculated from the pressure cell measurements and those measured by the force transducers tend to verify the adequacy of the pneumatic pressure cell calibration procedures.
    [Show full text]
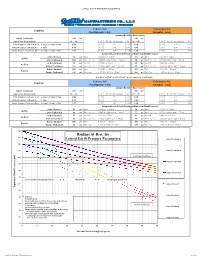
  • Lateral Earth Pressures
    LATERAL EARTH PRESSURE PARAMETERS Cohesive Soil Cohesionless Soil Condition (Non-Expansive Clay) (Granular Sand) Assumed Backfill Characteristics Approx Total Density 140 pcf 140 pcf Approximate Friction Angle 15º - 20º 15 Ka, Ko, Kp Averages 20 30º - 35º 30 Ka, Ko, Kp Averages 35 Active Pressure Coefficient, Ka = (1-sinϕ) / (1+sinϕ) = 1/Kp 0.54 0.59 0.54 0.49 0.30 0.33 0.30 0.27 At-Rest Pressure Coefficient, Ko = (1-sinϕ) 0.70 0.74 0.70 0.66 0.46 0.50 0.46 0.43 Passive Pressure Coefficient, Kp = (1+sinϕ) / (1-sinϕ) = 1/Ka 1.87 1.70 1.87 2.04 3.35 3.00 3.35 3.69 Estimated Lateral Earth Pressures (Equivalent Fluid Pressures) Active Drained 76 pcf Ka(γ) = 0.54(140) = 76 pcf 42 pcf Ka(γ) = 0.3(140) = 42 pcf Active Active Undrained 104 pcf Ka(γ - γ w) + γ w = 0.54(140 - 62.4) + 62.4 = 104 pcf 86 pcf Ka(γ - γ w) + γ w = 0.3(140 - 62.4) + 62.4 = 86 pcf At-Rest Drained 98 pcf Ko(γ) = 0.7(140) = 98 pcf 65 pcf Ko(γ) = 0.46(140) = 65 pcf At-Rest At Rest Undrained 117 pcf Ko(γ - γ w) + γ w = 0.7(140 - 62.4) + 62.4 = 117 pcf 98 pcf Ko(γ - γ w) + γ w = 0.46(140 - 62.4) + 62.4 = 98 pcf Passive Drained 262 pcf Kp(γ) = 1.87(140) = 262 pcf 468 pcf Kp(γ) = 3.35(140) = 468 pcf Passive Passive Undrained 145 pcf Kp(γ - γ w) = 1.87(140 - 62.4) = 145 pcf 260 pcf Kp(γ - γ w) = 3.35(140 - 62.4) = 260 pcf R = (0.5)(Ko)( γ)(H 2) = (0.5)(EFP)(H 2) = psf / lineal foot of wall length Cohesive Soil Cohesionless Soil Condition (Non-Expansive Clay) (Granular Sand) Assumed Backfill Characteristics Approx Total Density 110 pcf 110 pcf Approximate Friction Angle 15º -
    [Show full text]
  • Technical Cooperation Project : Landslide Adviser for Mauritius Manual
    Republic of Mauritius Landslide Management Unit: LMU, Ministry of Public Infrastructure and Land Transport: MPI TECHNICAL COOPERATION PROJECT : LANDSLIDE ADVISER FOR MAURITIUS MANUAL February 2018 Japan International Cooperation Agency (JICA) Kokusai Kogyo Co., Ltd. GE JR 18-025 CONTENTS 1. Manual for Survey and Countermeasures of Slope Failure Rock fall and Debris Flow 2. Procedure Manual for Landslide 3. Technical Guideline for Initial Survey 㻸㼛㼏㼍㼠㼕㼛㼚㻌㼛㼒㻌㻿㼠㼡㼐㼥㻌㻭㼞㼑㼍 20°0'0"E 30°0'0"E 40°0'0"E 50°0'0"E 60°0'0"E 70°0'0"E 80°0'0"E 20°0'0"N 20°0'0"N 10°0'0"N 10°0'0"N 0°0'0" 0°0'0" Republic of Mauritius 10°0'0"S 10°0'0"S 20°0'0"S 20°0'0"S 0500 1,000 2,000 km 20°0'0"E 30°0'0"E 40°0'0"E 50°0'0"E 60°0'0"E 70°0'0"E 80°0'0"E 㻰㼑㼠㼍㼕㼘㻌㻹㼍㼜 Rate of Currency Translation 1 USD = 32.1306 MUR = 110.69 JPY 100 MUR = 2.95035 USD = 326.57 JPY MUR: Mauritius Rupee As of 17 January 2018 JAPAN INTERNATIONAL COOPERATION AGENCY (JICA) MINISTRY OF PUBLIC INFRASTRUCTURE AND LAND TRANSPORT (MPI) Manual for Survey and Countermeasure of Slope Failure, Rock Fall and Debris Flow September 2017 Landslide Management Unit, Ministry of Public Infrastructure and Land Transport and KOKUSAI KOGYO CO., LTD. Preface Japan International Cooperation Agency (hereinafter JICA) has implemented the ‘Project of landslide management in Mauritius’ (hereinafter the Previous Project) from April 2012 to March 2015 as a part of the climatic change adaptation and disaster mitigation program for Small Island Developing States (SIDS).
    [Show full text]