DOCSLIB.ORG

Peter Guthrie Tait: a Knot's Tale Transcript

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Peter Guthrie Tait: a Knot's Tale Transcript Peter Guthrie Tait: A Knot's Tale Transcript Date: Wednesday, 31 October 2012 - 4:30PM Location: Barnard's Inn Hall 31 October 2012 Peter Guthrie Tait: A Knot's Tale Dr Julia Collins Good afternoon, everyone. Thank you very much for the invitation to come and speak at Gresham College. I have never been here before, so it is really exciting to see so many people. Of the three people that we are talking about this afternoon, I think Peter Guthrie Tait is the one who is least well-known. Put your hand up if you knew before today who Peter Guthrie Tait was… Okay, put your hand down if you are a member of the BSHM… [Laughter] I think, of the three, he is certainly the least well-known, so my job today is to tell you a bit about his life story, and in particular the contribution that he made to the mathematical theory of knots. At this point, I want to say, the caveat to that, I am not a historian and I am not a physicist. I do not understand the physics that Tait did, so I will be talking about his mathematics, and we can talk more about other things during the break. I also apologise to any Tait enthusiasts that there will be so many things about his life that I do not have time to fit into 45 minutes, so I apologise for that. I realise that I am the person standing between you and the alcoholic drinks in 45 minutes, so let me motivate this lecture to make you excited about what is coming up in my talk! [Recording plays] I am going to start the story in Edinburgh, but in modern times, with me, the narrator. This is the National Library of Scotland, where I started learning about Peter Guthrie Tait. I was pointed to this repository of knowledge by another historian called Maurice Eppel, and I was told that, in here, there was an envelope that Peter Guthrie Tait had enclosed some of his conjectures and that those conjectures had remained unopened for 100 years, and I wanted to go in there and find this envelope and find what was in there and why it was that no one had opened it, and so part of this lecture is the story of how I found the envelope and what was inside it. At first, I did not find the envelope I was looking for. I found some scribble on the back of a different envelope, which I was really excited by, and we will come back to this again. So it starts off with OT, and I was assuming that you would not know what that meant, but maybe you have got an idea from the previous lecture. More excitingly is this paragraph down here…”Can’t you come on Monday the present at the performance? An elliptical hole gives the rings in a state of vibration.” So, what is this experiment that he has been invited to? Who is it that has been invited whose experiment? That is what we are going to learn about today. Let us go back to 1876, which is the scene of this experiment, and in this lab in Edinburgh, there are two men in this room which is thick with smoke. We may make this room thick with smoke later today, if you are a good audience. The men in question are Peter Guthrie Tait and William Thomson, and what they would do in that room would change mathematical history. Just to set the scene, it is 1876. I do not know how many people were listening carefully to the timeline in the previous talk, but we have got Maxwell, who has been developing, in that decade, his theory of electromagnetism, unifying electricity, magnetism and light, and dealing with kinetic theory of gases. It has been six years since Maxwell developed the first colour photograph. Thomson, just one year before, had been knighted for his laying of the transatlantic telegraph cables on the ship, the Great Eastern, so he is actually called Lord Kelvin. I will interchange William Thomson and Lord Kelvin during the talk, so do not get confused. Darwin has published his Origin of Species only eight years previous, and Tait and Thomson, in that very year, have published their kind of magnum opus, their great textbook, the Treatise on Natural Philosophy, which redefined what physics meant at the time. It is 1867, and it is a really exciting time in science. One of the big questions that are on people’s minds is: what do atoms look like? No one has been able to look at one in a microscope, and there are some people who do not even believe that atoms really exist. There were all sorts of different theories going around at the time. Even for those people that do think atoms exist, there is a conversation about what atoms could look like. Suppose an atom was like a solid, hard ball, like that, what is it about these little balls that would explain the different kinds of matter that we see in the universe? Is it that an oxygen atom would look different from a nitrogen atom or an iron atom? This is the big question that was on people’s minds. During this lecture, I want you to keep that question in your minds. This lecture is going to be the story of the answer to that question of “What do atoms look like?” and the man, Peter Guthrie Tait, who was the catalyst for the discoveries that were made from that point. So, let us go back and start the story as it should have been started, at the beginning, in Dalkeith and Edinburgh, where two boys are born, just a couple of months apart. Dalkeith is just fifteen miles south of Edinburgh. It is a small town. This is its church, and that is where Peter Guthrie Tait was born, in April, and two months later, James Clerk Maxwell was born in India Street in Edinburgh. So they were born very close together. They both had the same kind of tragic childhood. We have already heard, Kelvin lost his mother when he was six years old. Tait last his father when he was six years old, which meant moving to Edinburgh to live with his uncle. Maxwell lost his mother when he was eight years old as well. So they all have this shared tragic childhood, but, in a way, it precipitated them to go and learn science from somebody else. Tait was heavily influenced by his uncle, who inspired in him a real love of natural philosophy and science. Tait and Maxwell both went to the same school, Edinburgh Academy, which still exists in Edinburgh today, and they were in different year groups, despite being pretty much exactly the same age, because Tait’s family enrolled him in school nice and early and so he got into the year group he should have been in, whereas Maxwell’s family were a bit behind, and by the time they tried to enrol Maxwell, the class was already completely full and he had to go into the year above. They were the same age, but they were in different years in school, and despite that, they met each other and they became extremely good friends. They were friendly rivals at the same time, competing to do well in their examinations. When they were sixteen years old, they both went to the University of Edinburgh to study Maths and Natural Philosophy, and their Natural Philosophy professor, as we have heard, was Forbes. In Edinburgh, at that time, the Natural Philosophy class was split into three divisions, so the idea was that you would enter in the third division and, as you became more knowledgeable, you would work your way up to the first division. Maxwell was a confident young man, and he realised he was too good for the third division, so he went straight in at the second division, but Tait had to go one better and he enrolled straight into the first division, despite being told otherwise by Forbes. Forbes said, “This is not a good idea – you should stick with Maxwell,” and he said, “No, I am good enough, I will be in the first division,” and he did well, and after only a year, he decided that he was ready to move to Cambridge and went to Peterhouse College, which is the same place where Kelvin had gone before and where Maxwell would follow him just a few years later. So in 1852, this series of events has meant that Tait has become the youngest ever person to be senior wrangler in the Mathematics Tripos exams, which means that he got top exam marks, and he was only twenty years and eight months old, and the record that he set was not bettered until 1936, when a nineteen year old became senior wrangler. Of the three, he was the only person who was senior wrangler, so both Maxwell and Tait only got second wrangler. This is a picture of Tait here, on the left-hand side. This is Steele, who got second place – he was another great scientist at the time. You can already see this wonderful figure that he cuts: he is a very tall, very imposing young man, and very confident. Based on the strength of his exam results, he became a Fellow of Peterhouse College, and started coaching other students as part of his duties as a Fellow.
Load more

Recommended publications
  • Tait's Flyping Conjecture for 4-Regular Graphs
    CORE Metadata, citation and similar papers at core.ac.uk Provided by Elsevier - Publisher Connector Journal of Combinatorial Theory, Series B 95 (2005) 318–332 www.elsevier.com/locate/jctb Tait’s flyping conjecture for 4-regular graphs Jörg Sawollek Fachbereich Mathematik, Universität Dortmund, 44221 Dortmund, Germany Received 8 July 1998 Available online 19 July 2005 Abstract Tait’s flyping conjecture, stating that two reduced, alternating, prime link diagrams can be connected by a finite sequence of flypes, is extended to reduced, alternating, prime diagrams of 4-regular graphs in S3. The proof of this version of the flyping conjecture is based on the fact that the equivalence classes with respect to ambient isotopy and rigid vertex isotopy of graph embeddings are identical on the class of diagrams considered. © 2005 Elsevier Inc. All rights reserved. Keywords: Knotted graph; Alternating diagram; Flyping conjecture 0. Introduction Very early in the history of knot theory attention has been paid to alternating diagrams of knots and links. At the end of the 19th century Tait [21] stated several famous conjectures on alternating link diagrams that could not be verified for about a century. The conjectures concerning minimal crossing numbers of reduced, alternating link diagrams [15, Theorems A, B] have been proved independently by Thistlethwaite [22], Murasugi [15], and Kauffman [6]. Tait’s flyping conjecture, claiming that two reduced, alternating, prime diagrams of a given link can be connected by a finite sequence of so-called flypes (see [4, p. 311] for Tait’s original terminology), has been shown by Menasco and Thistlethwaite [14], and for a special case, namely, for well-connected diagrams, also by Schrijver [20].
    [Show full text]
  • Alternating Knots
    ALTERNATING KNOTS WILLIAM W. MENASCO Abstract. This is a short expository article on alternating knots and is to appear in the Concise Encyclopedia of Knot Theory. Introduction Figure 1. P.G. Tait's first knot table where he lists all knot types up to 7 crossings. (From reference [6], courtesy of J. Hoste, M. Thistlethwaite and J. Weeks.) 3 ∼ A knot K ⊂ S is alternating if it has a regular planar diagram DK ⊂ P(= S2) ⊂ S3 such that, when traveling around K , the crossings alternate, over-under- over-under, all the way along K in DK . Figure1 show the first 15 knot types in P. G. Tait's earliest table and each diagram exhibits this alternating pattern. This simple arXiv:1901.00582v1 [math.GT] 3 Jan 2019 definition is very unsatisfying. A knot is alternating if we can draw it as an alternating diagram? There is no mention of any geometric structure. Dissatisfied with this characterization of an alternating knot, Ralph Fox (1913-1973) asked: "What is an alternating knot?" black white white black Figure 2. Going from a black to white region near a crossing. 1 2 WILLIAM W. MENASCO Let's make an initial attempt to address this dissatisfaction by giving a different characterization of an alternating diagram that is immediate from the over-under- over-under characterization. As with all regular planar diagrams of knots in S3, the regions of an alternating diagram can be colored in a checkerboard fashion. Thus, at each crossing (see figure2) we will have \two" white regions and \two" black regions coming together with similarly colored regions being kitty-corner to each other.
    [Show full text]
  • Crossing Number of Alternating Knots in S × I
    Pacific Journal of Mathematics CROSSING NUMBER OF ALTERNATING KNOTS IN S × I Colin Adams, Thomas Fleming, Michael Levin, and Ari M. Turner Volume 203 No. 1 March 2002 PACIFIC JOURNAL OF MATHEMATICS Vol. 203, No. 1, 2002 CROSSING NUMBER OF ALTERNATING KNOTS IN S × I Colin Adams, Thomas Fleming, Michael Levin, and Ari M. Turner One of the Tait conjectures, which was stated 100 years ago and proved in the 1980’s, said that reduced alternating projections of alternating knots have the minimal number of crossings. We prove a generalization of this for knots in S ×I, where S is a surface. We use a combination of geometric and polynomial techniques. 1. Introduction. A hundred years ago, Tait conjectured that the number of crossings in a reduced alternating projection of an alternating knot is minimal. This state- ment was proven in 1986 by Kauffman, Murasugi and Thistlethwaite, [6], [10], [11], working independently. Their proofs relied on the new polynomi- als generated in the wake of the discovery of the Jones polynomial. We usually think of this result as applying to knots in the 3-sphere S3. However, it applies equally well to knots in S2×I (where I is the unit interval [0, 1]). Indeed, if one removes two disjoint balls from S3, the resulting space is homeomorphic to S2 × I. It is not hard to see that these two balls do not affect knot equivalence. We conclude that the theory of knot equivalence in S2 × I is the same as in S3. With this equivalence in mind, it is natural to ask if the Tait conjecture generalizes to knots in spaces of the form S × I where S is any compact surface.
    [Show full text]
  • The Geometric Content of Tait's Conjectures
    The geometric content of Tait's conjectures Ohio State CKVK* seminar Thomas Kindred, University of Nebraska-Lincoln Monday, November 9, 2020 Historical background: Tait's conjectures, Fox's question Tait's conjectures (1898) Let D and D0 be reduced alternating diagrams of a prime knot L. (Prime implies 6 9 T1 T2 ; reduced means 6 9 T .) Then: 0 (1) D and D minimize crossings: j jD = j jD0 = c(L): 0 0 (2) D and D have the same writhe: w(D) = w(D ) = j jD0 − j jD0 : (3) D and D0 are related by flype moves: T 2 T1 T2 T1 Question (Fox, ∼ 1960) What is an alternating knot? Tait's conjectures all remained open until the 1985 discovery of the Jones polynomial. Fox's question remained open until 2017. Historical background: Proofs of Tait's conjectures In 1987, Kauffman, Murasugi, and Thistlethwaite independently proved (1) using the Jones polynomial, whose degree span is j jD , e.g. V (t) = t + t3 − t4. Using the knot signature σ(L), (1) implies (2). In 1993, Menasco-Thistlethwaite proved (3), using geometric techniques and the Jones polynomial. Note: (3) implies (2) and part of (1). They asked if purely geometric proofs exist. The first came in 2017.... Tait's conjectures (1898) T 2 GivenT1 reducedT2 alternatingT1 diagrams D; D0 of a prime knot L: 0 (1) D and D minimize crossings: j jD = j jD0 = c(L): 0 0 (2) D and D have the same writhe: w(D) = w(D ) = j jD0 − j jD0 : (3) D and D0 are related by flype moves: Historical background: geometric proofs Question (Fox, ∼ 1960) What is an alternating knot? Theorem (Greene; Howie, 2017) 3 A knot L ⊂ S is alternating iff it has spanning surfaces F+ and F− s.t.: • Howie: 2(β1(F+) + β1(F−)) = s(F+) − s(F−).
    [Show full text]
  • Knots, Molecules, and the Universe: an Introduction to Topology
    KNOTS, MOLECULES, AND THE UNIVERSE: AN INTRODUCTION TO TOPOLOGY AMERICAN MATHEMATICAL SOCIETY https://doi.org/10.1090//mbk/096 KNOTS, MOLECULES, AND THE UNIVERSE: AN INTRODUCTION TO TOPOLOGY ERICA FLAPAN with Maia Averett David Clark Lew Ludwig Lance Bryant Vesta Coufal Cornelia Van Cott Shea Burns Elizabeth Denne Leonard Van Wyk Jason Callahan Berit Givens Robin Wilson Jorge Calvo McKenzie Lamb Helen Wong Marion Moore Campisi Emille Davie Lawrence Andrea Young AMERICAN MATHEMATICAL SOCIETY 2010 Mathematics Subject Classification. Primary 57M25, 57M15, 92C40, 92E10, 92D20, 94C15. For additional information and updates on this book, visit www.ams.org/bookpages/mbk-96 Library of Congress Cataloging-in-Publication Data Flapan, Erica, 1956– Knots, molecules, and the universe : an introduction to topology / Erica Flapan ; with Maia Averett [and seventeen others]. pages cm Includes index. ISBN 978-1-4704-2535-7 (alk. paper) 1. Topology—Textbooks. 2. Algebraic topology—Textbooks. 3. Knot theory—Textbooks. 4. Geometry—Textbooks. 5. Molecular biology—Textbooks. I. Averett, Maia. II. Title. QA611.F45 2015 514—dc23 2015031576 Copying and reprinting. Individual readers of this publication, and nonprofit libraries acting for them, are permitted to make fair use of the material, such as to copy select pages for use in teaching or research. Permission is granted to quote brief passages from this publication in reviews, provided the customary acknowledgment of the source is given. Republication, systematic copying, or multiple reproduction of any material in this publication is permitted only under license from the American Mathematical Society. Permissions to reuse portions of AMS publication content are handled by Copyright Clearance Center’s RightsLink service.
    [Show full text]
  • Arxiv:1202.6488V4 [Math.GT] 11 Mar 2015 Ikinvariants Link 2 Introduction 1 Contents Invertibility
    Prime component-preservingly amphicheiral link with odd minimal crossing number Teruhisa KADOKAMI and Yoji KOBATAKE March 11, 2015 Abstract For every odd integer c 21, we raise an example of a prime component-preservingly ≥ amphicheiral link with the minimal crossing number c. The link has two components, and consists of an unknot and a knot which is ( )-amphicheiral with odd minimal crossing − number. We call the latter knot a Stoimenow knot. We also show that the Stoimenow knot is not invertible by the Alexander polynomials. Contents 1 Introduction 1 2 Link invariants 4 2.1 Kauffmanbracket.............................. 4 2.2 AlexanderandConwaypolynomials. 6 3 Stoimenow knots 7 4 Proof of Theorem 1.3 9 arXiv:1202.6488v4 [math.GT] 11 Mar 2015 5 Non-invertibility of Stoimenow knots 13 1 Introduction 3 Let L = K1 Kr be an oriented r-component link in S . A 1-component link is called a knot.∪···∪ For an oriented knot K, we denote the orientation-reversed knot by 3 K. If ϕ is an orientation-reversing homeomorphism of S so that ϕ(Ki) = εσ(i)Kσ(i) for− all i = 1,...,r where ε =+ or , and σ is a permutation of 1, 2,...,r , then L i − { } 2010 Mathematics Subject Classification: 57M25, 57M27. Keywords: component-preservingly amphicheiral link; minimal crossing number; Tait’s conjecture ; invertibility. 1 is called an (ε1,...,εr; σ)-amphicheiral link. A term “amphicheiral link” is used as a general term for an (ε1,...,εr; σ)-amphicheiral link. If ϕ can be taken as an involution (i.e. ϕ2 = id), then L is called a strongly amphicheiral link.
    [Show full text]
  • KNOTS from Combinatorics of Knot Diagrams to Combinatorial Topology Based on Knots
    2034-2 Advanced School and Conference on Knot Theory and its Applications to Physics and Biology 11 - 29 May 2009 KNOTS From combinatorics of knot diagrams to combinatorial topology based on knots Jozef H. Przytycki The George Washington University Washington DC USA KNOTS From combinatorics of knot diagrams to combinatorial topology based on knots Warszawa, November 30, 1984 { Bethesda, March 3, 2007 J´ozef H. Przytycki LIST OF CHAPTERS: Chapter I: Preliminaries Chapter II: History of Knot Theory This e-print. Chapter II starts at page 3 Chapter III: Conway type invariants Chapter IV: Goeritz and Seifert matrices Chapter V: Graphs and links e-print: http://arxiv.org/pdf/math.GT/0601227 Chapter VI: Fox n-colorings, Rational moves, Lagrangian tangles and Burnside groups Chapter VII: Symmetries of links Chapter VIII: Different links with the same Jones type polynomials Chapter IX: Skein modules e-print: http://arxiv.org/pdf/math.GT/0602264 2 Chapter X: Khovanov Homology: categori- fication of the Kauffman bracket relation e-print: http://arxiv.org/pdf/math.GT/0512630 Appendix I. Appendix II. Appendix III. Introduction This book is about classical Knot Theory, that is, about the position of a circle (a knot) or of a number of disjoint circles (a link) in the space R3 or in the sphere S3. We also venture into Knot Theory in general 3-dimensional manifolds. The book has its predecessor in Lecture Notes on Knot Theory, which were published in Polish1 in 1995 [P-18]. A rough translation of the Notes (by J.Wi´sniewski) was ready by the summer of 1995.
    [Show full text]
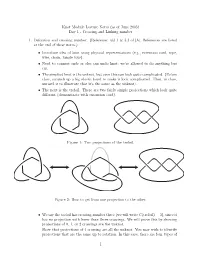
  • Knot Module Lecture Notes (As of June 2005) Day 1 - Crossing and Linking Number
    Knot Module Lecture Notes (as of June 2005) Day 1 - Crossing and Linking number 1. Definition and crossing number. (Reference: §§1.1 & 3.3 of [A]. References are listed at the end of these notes.) • Introduce idea of knot using physical representations (e.g., extension cord, rope, wire, chain, tangle toys). • Need to connect ends or else can undo knot; we’re allowed to do anything but cut. • The simplest knot is the unknot, but even this can look quite complicated. (Before class, scrunch up a big elastic band to make it look complicated. Then, in class, unravel it to illustrate that it’s the same as the unknot). • The next is the trefoil. There are two fairly simple projections which look quite different (demonstrate with extension cord). Figure 1: Two projections of the trefoil. Figure 2: How to get from one projection to the other. • We say the trefoil has crossing number three (we will write C(trefoil) = 3), since it has no projection with fewer than three crossings. We will prove this by showing projections of 0, 1, or 2 crossings are the unknot. Show that projections of 1 crossing are all the unknot. You may wish to identify projections that are the same up to rotation. In this case, there are four types of 1 Figure 3: Some 1-crossing projections. 1-crossing projection. If you also allow reflections, then there are only two types, one represented by the left column of Figure 3 and the other by any of the eight other projections. The crossing number two case is homework.
    [Show full text]
  • The Conway Polynomial and Amphicheiral Knots
    University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Doctoral Dissertations Graduate School 5-2016 The Conway Polynomial and Amphicheiral Knots Vajira Asanka Manathunga University of Tennessee - Knoxville, [email protected] Follow this and additional works at: https://trace.tennessee.edu/utk_graddiss Part of the Geometry and Topology Commons Recommended Citation Manathunga, Vajira Asanka, "The Conway Polynomial and Amphicheiral Knots. " PhD diss., University of Tennessee, 2016. https://trace.tennessee.edu/utk_graddiss/3721 This Dissertation is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a dissertation written by Vajira Asanka Manathunga entitled "The Conway Polynomial and Amphicheiral Knots." I have examined the final electronic copy of this dissertation for form and content and recommend that it be accepted in partial fulfillment of the requirements for the degree of Doctor of Philosophy, with a major in Mathematics. James R. Conant, Major Professor We have read this dissertation and recommend its acceptance: Morwen Thistlethwaite, Nikolay Brodskiy, Michael Berry Accepted for the Council: Carolyn R. Hodges Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) The Conway Polynomial and Amphicheiral Knots A Dissertation Presented for the Doctor of Philosophy Degree The University of Tennessee, Knoxville Vajira Asanka Manathunga May 2016 c by Vajira Asanka Manathunga, 2016 All Rights Reserved.
    [Show full text]
  • Knot Theory and Its Applications
    Alma Mater Studiorum Universita` degli Studi di Bologna Facolt`adi Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Tesi di Laurea in Geometria III Knot Theory and its applications Candidato: Relatore: Martina Patone Chiar.ma Prof. Rita Fioresi Anno Accademico 2010/2011 - Sessione II . Contents Introduction 11 1 History of Knot Theory 15 1 The Firsts Discoveries . 15 2 Physic's interest in knot theory . 19 3 The modern knot theory . 24 2 Knot invariants 27 1 Basic concepts . 27 2 Classical knot invariants . 28 2.1 The Reidemeister moves . 29 2.2 The minimum number of crossing points . 30 2.3 The bridge number . 31 2.4 The linking number . 33 2.5 The tricolorability . 35 3 Seifert matrix and its invariants . 38 3.1 Seifert matrix . 38 3.2 The Alexander polynomial . 44 3.3 The Alexander-Conway polynomial . 46 4 The Jones revolution . 50 4.1 Braids theory . 50 4.2 The Jones polynomial . 58 5 The Kauffman polynomial . 63 3 Knot theory: Application 69 1 Knot theory in chemistry . 69 4 Contents 1.1 The Molecular chirality . 69 1.2 Graphs . 73 1.3 Establishing the topological chirality of a molecule . 78 2 Knots and Physics . 83 2.1 The Yang Baxter equation and knots invariants . 84 3 Knots and biology . 86 3.1 Tangles and 4-Plats . 87 3.2 The site-specific recombination . 91 3.3 The tangle method for site-specific recombination . 92 Bibliography 96 List of Figures 1 Wolfagang Haken's gordian knot . 11 1.1 Stamp seal (1700 BC) .
    [Show full text]
  • States, Link Polynomials, and the Tait Conjectures a Thesis Submitted by Richard Louis Rivero to the Department of Mathematics H
    States, Link Polynomials, and the Tait Conjectures a thesis submitted by Richard Louis Rivero to the Department of Mathematics Harvard University Cambridge, Massachusetts in partial fulfillment of the requirements for the degree of Bachelor of Arts, with honors E-Mail: [email protected], Phone: 617-493-6256. For my grandfather, Louis A. Stanzione Contents Introduction 1 1. Motivating Ideas 1 2. Basic Notions in Link Theory 4 3. Acknowledgements 5 Chapter 1. States and Link Polynomials 7 1. States 7 2. The Bracket Polynomial 9 3. The Writhe 16 4. The Kauffman and Jones Polynomials 18 Chapter 2. The Tait Conjectures 21 1. Connected Projections 21 2. Reduced Projections 22 3. Alternating Links 23 4. The Tait Conjectures 24 5. Proof of the First Tait Conjecture 25 6. Proof of the Second Tait Conjecture 32 7. Applications of the Tait Conjectures 37 8. The Third Tait Conjecture 40 Bibliography 43 i 1 Introduction 1. Motivating Ideas At its core, this thesis is a study of knots, objects which human beings encounter with extraordinary frequency. We may find them on our person (in our shoelaces and neckties), or around our homes (as entangled telephone cords or Christmas tree lights). History, if not personal experience, teaches us that undoing knots can be a challenging and frustrating task: when Alexander the Great was unable to loose the famous Gordian knot by hand (a feat whose accomplisher, according to an oracle, would come to rule all of Asia), he cheated and cut it open with his sword. Still, a knot's same potential for intricacy serves the needs of scouts, sailors, and mountain climbers very well.
    [Show full text]
  • Knots, Graphs and Geometry
    Knots, Graphs and Geometry Abhijit Champanerkar Department of Mathematics, Mathematics Program, College of Staten Island, CUNY The Graduate Center, CUNY GC MathFest 2014 Nov 11, 2014 Two knots are equivalent if there is continuous deformation (ambient isotopy) of S3 taking one to the other. Goals: To classify knots upto equivalence. What is a knot ? A knot is a (smooth) embedding of the circle S1 in S3. Similarly, a link of k-components is a (smooth) embedding of a disjoint union of k circles in S3. Figure-8 knot Whitehead link Borromean rings What is a knot ? A knot is a (smooth) embedding of the circle S1 in S3. Similarly, a link of k-components is a (smooth) embedding of a disjoint union of k circles in S3. Figure-8 knot Whitehead link Borromean rings Two knots are equivalent if there is continuous deformation (ambient isotopy) of S3 taking one to the other. Goals: To classify knots upto equivalence. A given knot has many different diagrams. Two knot diagrams represent the same knot if and only if they are related by a sequence of three kinds of moves on the diagram called the Reidemeister moves. Knot Diagrams A common way to describe a knot is using a planar projection of the knot which is a 4-valent planar graph indicating the over and under crossings called a knot diagram. Two knot diagrams represent the same knot if and only if they are related by a sequence of three kinds of moves on the diagram called the Reidemeister moves. Knot Diagrams A common way to describe a knot is using a planar projection of the knot which is a 4-valent planar graph indicating the over and under crossings called a knot diagram.
    [Show full text]