Identifying Isoyield Environments for Field Pea Production
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
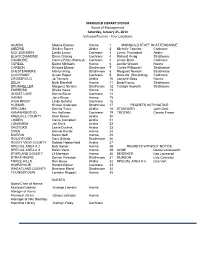
Board Minutes for the Year 2014
MARIGOLD LIBRARY SYSTEM Board of Management Saturday, January 25, 2014 Videoconference - Four Locations ACADIA Maxine Booker Hanna 1 MARIGOLD STAFF IN ATTENDANCE AIRDRIE Shelley Sweet Airdrie 2 Michelle Toombs Cochrane M.D. BIGHORN Lynda Lyster Cochrane 3 Lynne Thorimbert Airdrie BLACK DIAMOND Diane Osberg Cochrane 4 Richard Kenig Strathmore CANMORE Carney Raitz-Wakaryk Cochrane 5 Jessie Bach Cochrane CEREAL Elaine Michaels Hanna 6 Jenifer Waugh Hanna CARBON Richard Ekman Strathmore 7 Carlee Pilikowski Strathmore CHESTERMERE Marilyn King Strathmore 8 Margaret Newton Strathmore COCHRANE Susan Roper Cochrane 9 Nora Ott (Recording) Cochrane CROSSFIELD Jo Tennant Airdrie 10 Lorraine Betts Hanna DELIA Barb Marshall Hanna 11 Barb Froese Strathmore DRUMHELLER Margaret Nielsen Strathmore 12 Caleigh Haworth Strathmore EMPRESS Sheila Howe Hanna 13 GHOST LAKE Donna Bauer Cochrane 14 HANNA Jerry Kruse Hanna 15 HIGH RIVER Linda Schafer Cochrane 16 HUSSAR Kristen Anderson Strathmore 17 REGRETS WITH NOTICE IRRICANA Dennis Tracz Airdrie 18 STANDARD John Getz KANANASKIS I.D. Arn Hoffman Cochrane 19 TROCHU Connie Fraser KNEEHILL COUNTY Glen Keiver Airdrie 20 LINDEN Carrie Campbell Airdrie 21 LONGVIEW Jan Dyck Airdrie 22 OKOTOKS Leslie Duchak Airdrie 23 OYEN Dennis Punter Hanna 24 MORRIN Karen Neill Hanna 25 ROCKYFORD Gary Billings Strathmore 26 ROCKY VIEW COUNTY Debbie Habberfield Airdrie 27 SPECIAL AREA # 2 Bob Gainer Hanna 28 REGRETS WITHOUT NOTICE SPECIAL AREA # 3 Helen Veno Hanna 29 ACME Daniel Leronowich STARLAND COUNTY Lil Morrison Hanna 30 BEISEKER Leo Louwerse STRATHMORE Denise Peterson Strathmore 31 MUNSON Lyle Cawiezel THREE HILLS Ron Howe Airdrie 32 SPECIAL AREA # 4 Lisa Vert WAIPAROUS Sandra Barker Cochrane 33 WHEATLAND COUNTY Berniece Bland Strathmore 34 YOUNGSTOWN Lorraine Ruppert Hanna 35 GUESTS Board Chair of Hanna Municipal Library -Evange Lamson Hanna Manager of Hanna Municipal Library -Cheryl Johnson Hanna Manager of Nan Boothby Memorial Library -Kathryn Foley Cochrane MINUTES 1. -

Regular Council Meeting Minutes
ADOPTED MINUTES REGULAR COUNCIL MEETING Mountain View County Minutes of the Regular Council Meeting held on Wednesday, April 10, 2019, in the Council Chamber, 1408 Twp Rd. 320, Didsbury, AB. PRESENT: Reeve B. Beattie Councillor A. Aalbers (Deputy Reeve) Councillor D. Fulton Councillor P. Johnson Councillor A. Kemmere Councillor D. Milne ABSENT: Councillor G. Harris IN ATTENDANCE: J. Holmes, Chief Administrative Officer C. Atchison, Director, Legislative, Community, and Agricultural Services R. Baker, Director, Operational Services R. Beaupertuis, Director, Corporate Services M. Bloem, Director, Planning and Development Services A. Wild, Communications Coordinator G. Eyers, Executive Assistant CALL TO ORDER: Reeve Beattie called the meeting to order at 9:00 a.m. Reeve Beattie introduced Council and staff. AGENDA Reeve Beattie advised of the following amendments to the agenda: 13.1 Legal Matter - FOIP Act, Sections 21 Moved by Councillor Kemmere RC19-190 That Council adopt the agenda of the Regular Council Meeting of April 10, 2019 as amended. Carried. MINUTES Moved by Councillor Fulton RC19-191 That Council adopt the Minutes of the Regular Council Meeting of March 13, 2019. Carried. DELEGATIONS Alberta Election Candidates Reeve Beattie thanked the Election Candidates for coming to the meeting. He stated that Candidates are requested to provide a brief introduction regarding themselves and their platform for the Provincial election. The following provided five minutes presentations followed by questions from Council: Olds-Didsbury-Three -

Community Well-Being Survey
RED DEER COUNTY NEWS OFFICIAL NEWS FROM RED DEER COUNTY CENTRE NOVEMBER 2016 Community Well-Being Survey LOOKING FOR RESIDENT OPINIONS ON RECREATION, CULTURE, AND FAMILY SUPPORT SERVICES Red Deer County ensures that recreation, culture, and individual and family express their views on a wide range of topics that impact them directly”. support programs and services are available to all residents. Beginning Questionnaires will be mailed out to every household in the County. Each October 17, the County will be conducting a Community Well-being Survey package will include a letter of introduction, a questionnaire, and a to gauge the satisfaction levels around a number of different recreation, postage-paid return envelope. The survey will also be available online. If a culture, and family support services. resident does not receive a package, they are encouraged to contact the County office and one will be sent to them. The last consultation process of this type was in 2004, and information gathered at that time has helped to drive decision-making for over a All the information given through the survey will be confidential. Combined decade. Much has changed over that time, and now it is time to find out responses will be shared with County Council, and will help to set priorities what residents want the County’s recreation and culture priorities to be for recreation, culture, and individual and family support services for the over the next five to ten years. coming years. According to Community Services For updates, please see WHAT’S INSIDE: Manager Jo-Ann Symington, “The the Red Deer County Community Well-being Survey is a vital website or follow us on tool in assessing the needs of the Twitter with the hashtag: Open Houses............................Pg. -

2018 Municipal Affairs Population List | Cities 1
2018 Municipal Affairs Population List | Cities 1 Alberta Municipal Affairs, Government of Alberta November 2018 2018 Municipal Affairs Population List ISBN 978-1-4601-4254-7 ISSN 2368-7320 Data for this publication are from the 2016 federal census of Canada, or from the 2018 municipal census conducted by municipalities. For more detailed data on the census conducted by Alberta municipalities, please contact the municipalities directly. © Government of Alberta 2018 The publication is released under the Open Government Licence. This publication and previous editions of the Municipal Affairs Population List are available in pdf and excel version at http://www.municipalaffairs.alberta.ca/municipal-population-list and https://open.alberta.ca/publications/2368-7320. Strategic Policy and Planning Branch Alberta Municipal Affairs 17th Floor, Commerce Place 10155 - 102 Street Edmonton, Alberta T5J 4L4 Phone: (780) 427-2225 Fax: (780) 420-1016 E-mail: [email protected] Fax: 780-420-1016 Toll-free in Alberta, first dial 310-0000. Table of Contents Introduction ..................................................................................................................................... 4 2018 Municipal Census Participation List .................................................................................... 5 Municipal Population Summary ................................................................................................... 5 2018 Municipal Affairs Population List ....................................................................................... -

St2 St9 St1 St3 St2
! SUPP2-Attachment 07 Page 1 of 8 ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! .! ! ! ! ! ! SM O K Y L A K E C O U N T Y O F ! Redwater ! Busby Legal 9L960/9L961 57 ! 57! LAMONT 57 Elk Point 57 ! COUNTY ST . P A U L Proposed! Heathfield ! ! Lindbergh ! Lafond .! 56 STURGEON! ! COUNTY N O . 1 9 .! ! .! Alcomdale ! ! Andrew ! Riverview ! Converter Station ! . ! COUNTY ! .! . ! Whitford Mearns 942L/943L ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! 56 ! 56 Bon Accord ! Sandy .! Willingdon ! 29 ! ! ! ! .! Wostok ST Beach ! 56 ! ! ! ! .!Star St. Michael ! ! Morinville ! ! ! Gibbons ! ! ! ! ! Brosseau ! ! ! Bruderheim ! . Sunrise ! ! .! .! ! ! Heinsburg ! ! Duvernay ! ! ! ! !! ! ! ! 18 3 Beach .! Riviere Qui .! ! ! 4 2 Cardiff ! 7 6 5 55 L ! .! 55 9 8 ! ! 11 Barre 7 ! 12 55 .! 27 25 2423 22 ! 15 14 13 9 ! 21 55 19 17 16 ! Tulliby¯ Lake ! ! ! .! .! 9 ! ! ! Hairy Hill ! Carbondale !! Pine Sands / !! ! 44 ! ! L ! ! ! 2 Lamont Krakow ! Two Hills ST ! ! Namao 4 ! .Fort! ! ! .! 9 ! ! .! 37 ! ! . ! Josephburg ! Calahoo ST ! Musidora ! ! .! 54 ! ! ! 2 ! ST Saskatchewan! Chipman Morecambe Myrnam ! 54 54 Villeneuve ! 54 .! .! ! .! 45 ! .! ! ! ! ! ! ST ! ! I.D. Beauvallon Derwent ! ! ! ! ! ! ! STRATHCONA ! ! !! .! C O U N T Y O F ! 15 Hilliard ! ! ! ! ! ! ! ! !! ! ! N O . 1 3 St. Albert! ! ST !! Spruce ! ! ! ! ! !! !! COUNTY ! TW O HI L L S 53 ! 45 Dewberry ! ! Mundare ST ! (ELK ! ! ! ! ! ! ! ! . ! ! Clandonald ! ! N O . 2 1 53 ! Grove !53! ! ! ! ! ! ! ! ! ! ! ! ISLAND) ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! Ardrossan -

PL- 374 Date: February 26, 2008 Subject: NPA 587 to Overlay Npas 403 and 780 (Alberta, Canada) Related Previous Planning Letters: 364, 369
Number: PL- 374 Date: February 26, 2008 Subject: NPA 587 to Overlay NPAs 403 and 780 (Alberta, Canada) Related Previous Planning Letters: 364, 369 This Planning Letter supersedes Planning Letters 364 dated July 27, 2007, and 369 dated October 15, 2007. This revision makes changes to the Carriers' and Test numbers table to include MTS Allstream test numbers. Carrier Test Number MTS Allstream 587-810-8378 (TEST) MTS Allstream 587-810-2455 (BILL) In Telecom Decision CRTC 2007-42, Code relief for area codes 403 and 780 – Alberta, dated 14 June 2007, the Canadian Radio-television and Telecommunications Commission (CRTC) approved the introduction of a new area code for Alberta, Canada to the regions currently served by area codes 403 and 780. The new area code 587 assigned by the North American Numbering Plan Administration (NANPA) will be implemented in a "distributed overlay" over the entire province of Alberta covering both area codes 403 and 780 on the relief date of 19 September 2008. Maps showing the area served by NPAs 403, 780 and the new overlay NPA 587 as well as lists of exchange areas in each area code in Alberta are attached to this letter. Prior to mandatory 10-digit local dialling, callers dialling local calls with 7 digits will hear a network announcement notifying them to dial local calls with 10-digits in the future, after which their calls will be completed. Canadian carriers operating in NPAs 403 and 780 in Alberta will start providing this network announcement no earlier than 23 June 2008 and no later than 27 June 2008, and maintain it until mandatory 10-digit local dialling is introduced no earlier than 8 September 2008 and no later than 12 September 2008. -

Disposition 26099-D01-2020 Apex Acknowledgment of Rate Rider A
November 19, 2020 Disposition 26099-D01-2020 Irv Richelhoff Supervisor, Business Development Apex Utilities Inc. 5509 45 St. Leduc, Alta. T9E 6T6 Dear Irv Richelhoff: Apex Utilities Inc. Franchise Fee Rate Rider A Amendment for Town of Two Hills – Effective January 1, 2021 Proceeding 26099 Acknowledgment of rate schedule 1. The Alberta Utilities Commission received your filing for information purposes dated November 18, 2020, of an amendment to the Apex Utilities Inc. franchise fee Rate Rider A. The application identified a franchise fee change for the Town of Two Hills, effective January 1, 2021: Municipality Franchise fee collection percentage Effective date Town of Two Hills 15% Existing 23% January 1, 2021 2. The Town of Two Hills has notified customers of the change in the franchise fee through publication of two notices in the Vegreville News Advertiser more than 45 days prior to the proposed implementation date of January 1, 2021. 3. Additionally, the Town of Two Hills has the ability to revise the franchise fee on an annual basis pursuant to Article 4(c) of the Natural Gas Distribution System Franchise Agreement. The Commission agreed with the ability to increase the franchise fee on an annual basis in EUB Order U2005-134.1 1 EUB Order U2005-134: AltaGas Utilities Inc. and the Town of Two Hills Franchise Agreement and Rate Rider A, EUB Order U2005-134. Alberta Utilities Commission November 19, 2020 Page 2 of 3 4. The application for a revised franchise fee Rate Rider A is accepted as a filing for information. The revised franchise fee Rate Rider A schedule is attached as Appendix 1. -

July 2020 Edition Volume 6
Champion Chronicle Box 367 Champion, AB T0l 0R0 Volume 6 July 2020 Edition Today, as I write this, it is July 31, 2020. The Village welcomes Clever Scoops Ice Cream which will be open today at 10am to huge lines. The location will provide a great break from not only the heat but the months everyone has endured trying to stay safe and healthy. The Champion Convenience Store has been busy serving local people as well as many from the Little Bow Resort and our own park which has been nearly full or full on most weekends. The pool is open with a modified schedule and the library is as well. This “new normal” at least is starting to give us all a feeling of what life was like before. It has been great connecting with people again…in person. Provincially and locally we have seen the number of cases climb back up. There are just over 1,400 active cases in the province and 10 of the 25 cases we have seen in the County are still active. Champion has many new visitors which is a great thing. Wear a mask when it makes sense, use hand sanitizer or wash your hands as much as you can and finally, stay 6 feet apart. More importantly, go get an ice cream, it’s hot out there. Patrick Bergen CAO, Village of Champion JULY 1, 2020 CANADA POST AGREEMENT #43737522 Thank you to CiB for this beautiful addition to the flower bed at Heritage Park. SUBSCRIPTION RATES: Single Copy - $2.00 (available at the Village Office & Post Office) Yearly - Champion Residents $20.00 Outside Champion (Canada) $25.00 US Residents $60.00 Emailed Copy $12.00 HOW TO REACH US: Email - [email protected] Regular Mail - Champion Chronicle c/o Village of Champion Box 367 Champion, Alberta T0L 0R0 Drop Off - Items may be left in the Village of Champion office drop box ADVERTISING RATES: ONE TIME INSERT ANNUAL Business Card Directory $5.00 $60.00 Quarter Page $7.50 $75.00 Half Page $9.00 $90.00 Full Page $15.00 $150.00 FREE ITEMS: Event notices, announcements (wedding, anniversary, births, showers, etc.), thank you notices, news items and articles of interest. -

Published Local Histories
ALBERTA HISTORIES Published Local Histories assembled by the Friends of Geographical Names Society as part of a Local History Mapping Project (in 1995) May 1999 ALBERTA LOCAL HISTORIES Alphabetical Listing of Local Histories by Book Title 100 Years Between the Rivers: A History of Glenwood, includes: Acme, Ardlebank, Bancroft, Berkeley, Hartley & Standoff — May Archibald, Helen Bircham, Davis, Delft, Gobert, Greenacres, Kia Ora, Leavitt, and Brenda Ferris, e , published by: Lilydale, Lorne, Selkirk, Simcoe, Sterlingville, Glenwood Historical Society [1984] FGN#587, Acres and Empires: A History of the Municipal District of CPL-F, PAA-T Rocky View No. 44 — Tracey Read , published by: includes: Glenwood, Hartley, Hillspring, Lone Municipal District of Rocky View No. 44 [1989] Rock, Mountain View, Wood, FGN#394, CPL-T, PAA-T 49ers [The], Stories of the Early Settlers — Margaret V. includes: Airdrie, Balzac, Beiseker, Bottrell, Bragg Green , published by: Thomasville Community Club Creek, Chestermere Lake, Cochrane, Conrich, [1967] FGN#225, CPL-F, PAA-T Crossfield, Dalemead, Dalroy, Delacour, Glenbow, includes: Kinella, Kinnaird, Thomasville, Indus, Irricana, Kathyrn, Keoma, Langdon, Madden, 50 Golden Years— Bonnyville, Alta — Bonnyville Mitford, Sampsontown, Shepard, Tribune , published by: Bonnyville Tribune [1957] Across the Smoky — Winnie Moore & Fran Moore, ed. , FGN#102, CPL-F, PAA-T published by: Debolt & District Pioneer Museum includes: Bonnyville, Moose Lake, Onion Lake, Society [1978] FGN#10, CPL-T, PAA-T 60 Years: Hilda’s Heritage, -

Long Term Adequacy Report
Long Term Adequacy Report August 2020 Introduction The following report provides information on the long term adequacy of the Alberta electric energy market. The report contains metrics that include tables on generation projects under development and generation retirements, an annual reserve margin with a five year forecast period, a two year daily supply cushion, and a two year probabilistic assessment of the Alberta Interconnected Electric System (AIES). The Long Term Adequacy (LTA) Metrics provide an assessment and information that can be used to facilitate further assessments of long term adequacy. This report is updated quarterly in February, May, August, and November. Inquiries on the report can be made at [email protected]. *All metrics have been updated and use the most recent corporate load forecast the 2019 LTO found at https://www.aeso.ca/grid/forecasting. Summary of Changes since Previous Report New Generation and Retirements Metric Projects completed and removed from list: Keyera West Pembina 359S Gas Turbine Gas FortisAlberta 895S Suffield DG PV FortisAlberta Innisfail 214S DER Solar Maxim Power Milner Gas FortisAlberta 257S Hull DER Solar FortisAlberta Vauxhall Solar DER ENMAX Shepard Gas Upgrade Generation Projects moved to “Active Construction”: ENMAX Crossfield CRS3 Battery Storage Greengate Travers MPC Solar TransAlta Windrise MPC Wind Generation projects moved to “Regulatory Approval”: TransAlta Sundance Unit 5 Gas TransAlta Keephills Unit 1 Gas FortisAlberta Fieldgate 824S DER Gas Sequoia Energy Schuler -

September 9, 2020 FREE Monday to Saturday 9:00 AM to 6:00 PM
Virus & Malware Removal COMPUTER PROBLEMS? Computer Repair Have a Virus? Spyware Trouble? Computer Just Running Slow? Backup & Restore Wireless Networks Computer Upgrades Data Recovery 403.924.HELP (4357) Remote Support 403 Main Street, Three Hills Same Day Appointments [email protected] | www.vincovi.com We make house calls and also offer a pickup & drop-off service Y R C N PETERS 403.443.2433 419 Main St., Three Hills PHARMACY [email protected] THE We highly encourage all P T H customers wear a mask when Volume 107 - Number 50 you come into the store! Wednesday,CAPITAL September 9, 2020 FREE Monday to Saturday 9:00 AM to 6:00 PM Bus: 403-556-3371 Annual awards presented by Kneehill Minor Hockey Cell: by Roger Wilkins 403-443-0180 Kneehill Minor Hockey President www.oldsgm.com Hi everyone I am Roger Wilkins Arlin Koch - New/Used Sales your Kneehill Minor Hockey Three Hills / Olds / Kneehill County President. This year I have the privilege of announcing the recipients of two awards. The Tammy Kolke Spirit Of KMHA Award and the Dave P3 Evans Coach of the Year award. The “Tammy Kolke Spirit of KMHA Award” is awarded annually TROCHU to the member of KMHA or the community member who displays HOUSING outstanding enthusiasm and CORPORATION commitment to Minor Hockey within our association. UPDATE This year's recipients were Marvin Franke and Scott Orme. Marvin has been seen at the Trochu Arena over the past 20 years as the arena attendant and Kneehill Minor Hockey Association present its U18 (Midget) graduating players with a jersey. -

Convocation 2020 Program, You Can Sincerely Hope You Can Share and Celebrate This Achievement Goal
2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200 2200