Fluency with Rational Number Arithmetic

Unit Plan Mathematics Unit: 5 Grade: 7 Fluency with rational number arithmetic Solve multistep problems with positive and negative rational numbers in any form

Solve one‐variable equations of the form px + q = r and p(x + q) = r fluently

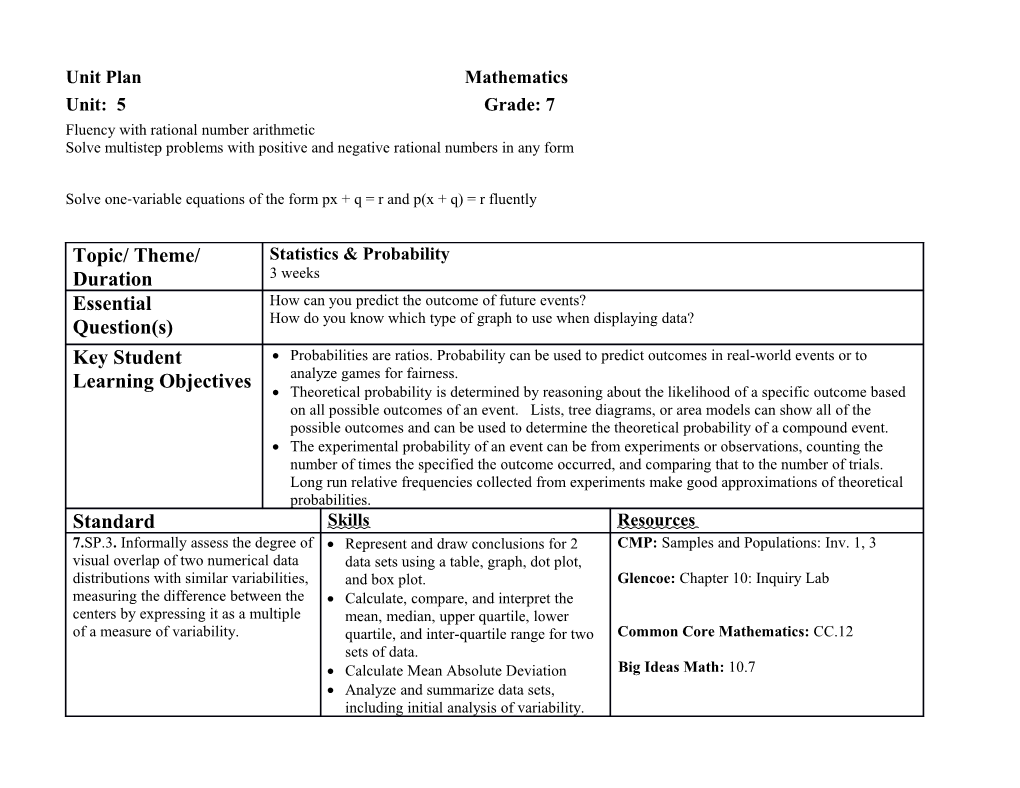
Topic/ Theme/ Statistics & Probability Duration 3 weeks Essential How can you predict the outcome of future events? Question(s) How do you know which type of graph to use when displaying data? Key Student  Probabilities are ratios. Probability can be used to predict outcomes in real-world events or to Learning Objectives analyze games for fairness.  Theoretical probability is determined by reasoning about the likelihood of a specific outcome based on all possible outcomes of an event. Lists, tree diagrams, or area models can show all of the possible outcomes and can be used to determine the theoretical probability of a compound event.  The experimental probability of an event can be from experiments or observations, counting the number of times the specified the outcome occurred, and comparing that to the number of trials. Long run relative frequencies collected from experiments make good approximations of theoretical probabilities. Standard Skills Resources 7.SP.3. Informally assess the degree of  Represent and draw conclusions for 2 CMP: Samples and Populations: Inv. 1, 3 visual overlap of two numerical data data sets using a table, graph, dot plot, distributions with similar variabilities, and box plot. Glencoe: Chapter 10: Inquiry Lab measuring the difference between the  Calculate, compare, and interpret the centers by expressing it as a multiple mean, median, upper quartile, lower of a measure of variability. quartile, and inter-quartile range for two Common Core Mathematics: CC.12 sets of data.  Calculate Mean Absolute Deviation Big Ideas Math: 10.7  Analyze and summarize data sets, including initial analysis of variability.  Informally assess the degree of visual overlap of two numerical data distributions with similar variability, measuring the difference between the centers by expressing it as a multiple of a measure of variability. 7. SP.4. Use measures of center and  Compare two sets of data using measures CMP: Samples and Populations: Inv. 1 measures of variability for numerical of center and variability data from random samples to draw  Draw informal comparative inferences Glencoe: Chapter 10: Lesson 4 informal comparative inferences about about two populations two populations.  Use measures of center and measures of variability for numerical data from Common Core Mathematics: Activity Lab random samples to draw informal 1.10b comparative inferences about two populations. For example, decide whether Big Ideas Math: 10.7 the words in a chapter of a seventh-grade science book are generally longer than the words in a chapter of a fourth-grade science book 7. SP.5. Understand that the  Explain how the probability of an event CMP: What Do You Expect?: Inv. 2, 4, 5 probability of a chance event is a is expressed as a fraction. number between 0 and 1 that  Represent the probability of events that expresses the likelihood of the event are impossible, unlikely, likely and Glencoe: Chapter : Lesson 1, 5 occurring. Larger numbers indicate certain using rational numbers from 0 to greater likelihood. A probability near 1. 0 indicates an unlikely event, a  Understand that the probability of a Common Core Mathematics: 12.1 probability around ½ indicates an chance event is a number between 0 and event that is neither unlikely nor 1 that expresses the likelihood of the Big Ideas Math: 10.1, 10.2, 10.3 likely, and a probability near 1 event occurring. Larger numbers indicate indicates a likely event. greater likelihood. A probability near 0 indicates an unlikely event, a probability around 1/2 indicates an event that is neither unlikely nor likely, and a probability near 1 indicates a likely event. 7. SP.6. Approximate the probability  Define theoretical probability and CMP: What Do You Expect?: Inv. 1, 2, 3, 4 of a chance event by collecting data on proportions the chance process that produces it  Design, perform, and collect data on a Glencoe: Chapter 9: Inquiry Lab and observing its long-run relative chance event frequency, and predict the  Analyze data from tables (frequency), approximate relative frequency given graphs and plots to determine Common Core Mathematics: 12.1, 12.2. the probability. probabilities of an event Activity Lab 12.2a  Use probability to predict outcomes of long-run or repeated/ larger events Big Ideas Math: 10.3  Organize collected data from experiments performed in tables, graphs, and plots.  Compare theoretical and experimental probability using the “Law of Large Numbers.”  Use theoretical probability and proportions to make approximate predictions.  Approximate the probability of a chance event by collecting data on the chance process that produces it and observing its long-run relative frequency, and predict the approximate relative frequency given the probability. For example, when rolling a number cube 600 times, predict that a 3 or 6 would be rolled roughly 200 times, but probably not exactly 200 times. 7. SP.7. Develop a probability model  Predict frequencies of outcomes based on CMP: What Do You Expect?: Inv. 3,5 and use it to find probabilities of theoretical probability events. Compare probabilities from a  Recognize an appropriate design to Glencoe: Chapter : Lesson 1, 2 model to observed frequencies; if the conduct an experiment with simple agreement is not good, explain probability events. possible sources of the discrepancy.  Develop a probability model to predict Common Core Mathematics: 12.2. Activity a. Develop a uniform probability outcomes based on a series of random Lab 12.2a model by assigning equal probability events (experimental probability). to all outcomes, and use the model to  Use a variety of experiments to explore Big Ideas Math: 10.2, 10.3 determine probabilities of events. the relationship between experimental b. Develop a probability model (which and theoretical probabilities and the may not be uniform) by observing affect of sample size on this relationship. frequencies in data generated from a  Recognize the frequency of outcomes chance process. based on theoretical probability.  Compare outcomes from theoretical to experimental probability.  Develop a uniform probability model by assigning equal probability to all outcomes, and use the model to determine probabilities of events. For example, if a student is selected at random from a class, find the probability that Jane will be selected and the probability that a girl will be selected 7. SP.8. Find probabilities of  Compare frequency of events based on a CMP: What Do You Expect?: Inv. 1, 2, 3, 4, 5 compound events using organized mode. lists, tables, tree diagrams, and  Develop a uniform probability model by Glencoe: Chapter : Lesson 3, 4, 5, 6, 7 simulation. assigning equal probability to all a. Understand that, just as with simple outcomes and use it to determine events, the probability of a compound probability of events. Common Core Mathematics: 12.3, 12.4 event is the fraction of outcomes in the  Develop a non-uniform probability model sample space for which the compound by assigning unequal probability to all Big Ideas Math: 10.4, 10.5 event occurs. outcomes b. Represent sample spaces for  Explain and justify discrepancy of events compound events using methods such from observed frequencies. as organized lists, tables and tree  Compare probability from models to diagrams. For an event described in observed frequencies everyday language (e.g., “rolling  Develop a probability model (which may double sixes”), identify the outcomes not be uniform) by observing frequencies in the sample space which compose in data generated from a chance process. the event. For example, find the approximate c. Design and use a simulation to probability that a spinning penny will land generate frequencies for compound heads up or that a tossed paper cup will events. land open-end down. Do the outcomes for the spinning penny appear to be equally likely based on the observed frequencies? Vocabulary Biased sample, box and whisker plots, complementary events, compound events, dependent events, dot plot, experimental probability, fair, fundamental counting principle, independent events, inter-quartile range, outcome, population, probability, random, sample space, simple event, standard deviation, statistics, survey, theoretical probability, tree diagram Sequence of Key Learning EXPERIMENTAL AND THEORETICAL PROBABILITIES Activities Understand experimental and theoretical probabilities For an event described in everyday language, identify the outcomes in a sample space that compose the event Interpret experimental and theoretical probabilities and the relationship between them and recognize that experimental probabilities are better estimates of theoretical probabilities when they are based on larger numbers Realize that the probability of simple events is a ratio of favorable outcomes to all outcomes in the sample space Recognize that the probability of a chance event is a number between 0 and 1 that expresses the likelihood of the event occurring Approximate the probability of a chance event by collecting data on the chance process that produces it and observing its long-run relative frequency, and predict the approximate relative frequency given the probability Determine the fairness of a game REASONING WITH PROBABILITY Represent sample spaces for simple and compound events and find probabilities using organized lists, tables, tree diagrams, area models, and simulation Realize that, just as with simple events, the probability of a compound event is a ratio of favorable outcomes to all outcomes in the sample space Analyze situations that involve two or more stages (or actions) called compound events Use probability to calculate the long-term average of a game of chance Determine the expected value of a probability situation Use probability and expected value to make a decision Activities/Tasks Investigation 1: A First look at Chance Choosing Cereal: Tossing Coins to Find Probabilities Tossing Paper Cups: Finding More Probabilities One More Try: Finding Experimental Probabilities Analyzing Events: Understanding Equally Likely Investigation 2: Experimental and Theoretical Probability Predicting to Win: Finding Theoretical Probabilities Choosing Marbles: Developing Probability Models Winning the Bonus Prize: Using Strategies to Find Theoretical Probabilities Winning the Bonus Prize: Using Strategies to Find Theoretical Probabilities Investigation 3: Making Decisions with Probability Designing a Spinner to Find Probabilities Making Decisions: Analyzing Fairness Roller Derby: Analyzing a Game Scratching Spots: Designing and Using a Simulation Investigation 4: Analyzing Compound Events Using an Area Model Drawing Area Models to Find the Sample Space Making Purple: Area Models and Probability One-and-One Free-Throws: Simulating a Probability Situation Scoring Points: Finding Expected Value Investigation 5: Binomial Outcomes Guessing Answers: Finding More Expected Values Ortonville: Binomial Probability A Baseball Series: Expanding Binomial Probability Note: Standards in bold are identified as major standards. Standards with checkmarks are standards recommended for greater emphasis