Linear Acceleration
Graphical Analysis of Acceleration : Velocity vs Time Graphs
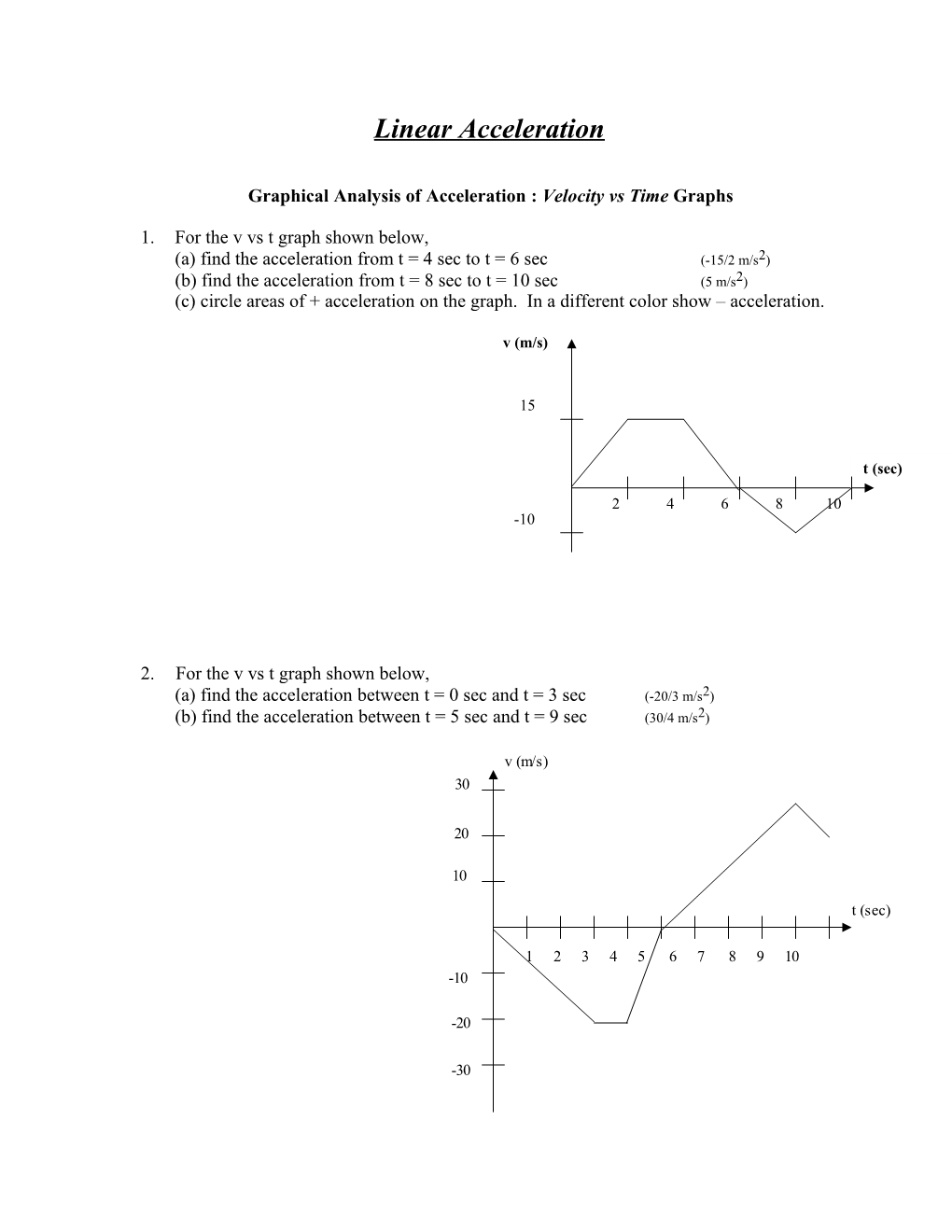
1. For the v vs t graph shown below, (a) find the acceleration from t = 4 sec to t = 6 sec (-15/2 m/s2) (b) find the acceleration from t = 8 sec to t = 10 sec (5 m/s2) (c) circle areas of + acceleration on the graph. In a different color show – acceleration.
v (m/s)
15
t (sec)
2 4 6 8 10 -10
2. For the v vs t graph shown below, (a) find the acceleration between t = 0 sec and t = 3 sec (-20/3 m/s2) (b) find the acceleration between t = 5 sec and t = 9 sec (30/4 m/s2)
v (m/s) 30
20
10
t (sec)
1 2 3 4 5 6 7 8 9 10 -10
-20
-30 3. For the v vs t graph shown below, (a) find the acceleration from t = 1 sec to t = 4 sec (2/3 m/s2) (b) find the acceleration from t = 5 sec to t = 7 sec (-4 m/s2)
v (m/s) 6
4
2
t (sec)
1 2 3 4 5 6 7 - 2
- 4
Graphical Analysis of Acceleration : Position vs Time Graphs
For each graph, describe the nature of the velocities and accelerations seen.
x
t
x
t Reference : Visually Identifying Acceleration on v vs t and x vs t Graphs
Case 1 : acceleration = 0
Slope of v vs t = 0 … no v There is no change in the slope of x vs t v v x x
Case 2 : acceleration is (+) Slope of v vs t is (+) The slope of x vs t gets more (+) or less (-) v v Speeds up in the (+) Slows down in the (-) Slows down in the (-) x direction x direction direction
Speeds up in the (+) direction
Case 3 : acceleration is (-) Slope of v vs t is (-) The slope of x vs t gets less (+) or more (-) v v Speeds up in the (-) Slows down in the Speeds up in the direction x (+) direction x (-) direction
Slows down in the (+) direction Linear Acceleration – Mathematical Equations built from understanding graphs
Most understand acceleration commonly as ‘speeding up’. But in physics, we know acceleration means more than just that. An acceleration is any change in velocity over an interval of time. So, an object can be said to accelerate when it speeds up, slows down, or changes direction (as in circular motion).
The relationship we found from graphical analysis is :
a = Δv/Δt (since it is the slope of the v vs. t graph, with units of m/sec2)
if we rearrange this equation, using Δv = vf - vi we get
vf = vi + at equation #1
Try the following set of problems based on these ideas:
1. What is the acceleration of Shain’s car that goes from 0 to 27 m/sec (i.e., 60 mph) in 6 seconds?
(4.5 m/s2)
2. If Bobby starts from rest and accelerates uniformly at 3 m/s2, how fast is he going after 2.4 seconds?
(7.2 m/s)
3. A rocket accelerates at 34 m/s2 , from a speed of 3500 m/s to 5200 m/s. How much time did it take?
(50 seconds)
4. A running back needs to come to a stop, from a speed of 9 m/s. If this takes 0.25 seconds, what is his acceleration? (-36 m/s2)
5. Chris, a motorcyclist, accelerates at 2 m/s2 for 10 seconds, starting at speed = 5 m/sec. (a) What speed does he reach at the end of the 10 seconds? (b) How far did he ride in this time?
(25 m/s ; 150 m) Linear Acceleration – Finding Displacement from v vs. t graphs
30
20 10
v (m/s)
1 2 3 4 5 6 7 8 9 10 t (sec) -10
Look at the v vs. t graph above. We can see that an object traveled at a velocity of +20 m/s for 5 seconds. Can we use this information to determine the displacement of the object?
A quick look will allow us to see that the object displaced 100m, using v = x/t, and solving for x.
This result can be also be calculated graphically by finding the area ‘under’ the curve!
30 x is the area ‘under the v vs. t curve!
20 10
v (m/s)
1 2 3 4 5 6 7 8 9 10 t (sec) -10 Let’s try one more, this time including negative velocity too…. 30 x for the first 5 seconds is the area under the v vs. t curve, which is 100m.
20 10 6 7 8 9 10 v (m/s)
1 2 3 4 5 6 7 8 9 t (sec) -10
x for the next 5 seconds is the area under the v vs. t curve, which is -50 m!
So over the entire 10 seconds the total displacement is [100m + -50m] = +50 m.
Questions: a. What is the displacement from t = 4 to t = 8 seconds? (-10 m) b. What is the displacement from t = 2 to t = 7 seconds? (40 m) c. If the object begins at position x = 43, where will it be after 7 seconds? (@ x=123) d. If the object is at position x = 10 at 5 sec, where is it when t=8? (@ x=-20) This graphical method of analysis can be used for v vs. t graphs, even when v is not constant!
30
20 10
v (m/s)
1 2 3 4 5 6 7 8 9 10 t (sec) -10
For the constant acceleration from 0 to 10 m/s2 as shown, the displacement over 6 seconds is the area of the shaded triangle. A = ½ bh = ½ (6 sec)(10 m/s) = 30 m!
Interestingly, we can use this method of analysis to create mathematical equations!
vf
vi
v (m/s)
t t (sec)
The line represents a constant acceleration from any velocity vi to any velocity vf over time t. As before, the area under the curve represents displacement of the object over the time interval!
Since the shaded area is a trapezoid, we can use Atrapezoid = ½ (b1 + b2)h to find the area. The trapezoid area equation becomes:
x = ½ (vi + vf) t ∆x= ½ (vi + vf) t Equation #2 (based on area under v vs t graph)
Try the next two problems using this relationship.
6. Bianca steals Shain’s car and takes it on a joyride at 9 m/s (20 mph) when she sees Zach asleep in the road. She slams on the brakes, coming to a stop in 2 seconds, leaving Zach unharmed. Find
(a) the car’s acceleration (b) how far the car traveled in coming to a halt.
2 (-4.5 m/s ; 9 m)
7. Repeat part (b) of problem #6 if Bianca’s car is initially moving (a) 4.5 m/s (half as fast) (b) 27 m/s (3 times as fast)
(2.25 m, 81 m)
Exercise : In the space below, derive the 3rd and 4th formulas shown below by algebraically combining equations #1 and #2 (we did it in class together too!)
Equation #3 Equation #4
2 2 2 ∆x = vit + (1/2)at vf = vi + 2a∆x Using these 4 equations of constantly accelerated motion, finish the rest of the problem set. note - When using these formulas, we must have 3 given values. Look for “hidden givens” based on the wording of the problem, if not given them directly.
8. On the way to the movies, Sara’s car runs out of gas. Her car, initially moving at a speed of 60 m/s 2 gradually slows down at a rate of 0.5 m/s for a period of 1 minute. Find:
(a) how far the car moved in this time (b) the car’s speed at the end of this time
(2700 m ; 30 m/s)
9. Thomas’ bicycle crests a hill with a speed of 2 m/s. He moves with constant acceleration until the bottom of the hill when his speed reaches 8 m/s. If the hill is 12 m long, what was his acceleration?
(2.5 m/s2)
10. Megan’s car starts from rest and travels for 5.0 s with a uniform acceleration of +1.5 m/s2. She then applies the brakes, causing an acceleration of -2.0 m/s2. If the brakes are applied for 3.0 s, what speed is the car going at the end of the 3s and how far is it from the point it started from?
(1.5 m/s, 32.25 m total)
11*. Joe stands on his ice skates on a frozen lake, when Tyler skates by with a puck at 12 m/s. Joe takes 3s to make up his mind to chase him. If he accelerates uniformly at 4 m/s2 a) how long does it take for him to catch up? b) how far away from his starting point are they when they’re even?
(8.2 s, 134 m) Gravitational Acceleration
12. Joel has had it, and finally drops Will down a well. How far will he fall in the first 4 seconds of free fall?
(-80 m)
13. How fast is Cait moving after stepping off an Olympic diving platform when she hits the water? (The platform is 10 meters above the water.)
(-14 m/s)
14. Ja-Vaughn rolls a ball at 8 m/sec up an incline. If it takes the ball 3 seconds to stop while rolling up the incline, determine the length of the incline.
The acceleration along an incline is NOT –10 m/s2. Why? Because the motion is not due to gravity only. .. the inclination matters as well!!! Think about it !
(12 m) 15. Victoria serves a ball straight up in the air with a speed of 20 m/sec. (a) How long is it in the air (assuming it returns to its starting point)?
If the motion ends where it started, the displacement is 0!!!
(b) How high does it rise? (c) What is the ball’s displacement between t = 1.5 sec and t = 3 sec?
(4 sec ; 20 m ; -3.75 m) 16. She then throws it down from a bridge with a speed of 30 m/sec. (a) How far away will it be after 2 seconds? (b) How fast is it moving after 4 seconds?
(-80 m ; -70 m/s)
17. Bored, she goes to the top of the Empire State Building, which is about 330 meters high, and drops it. Neglect air resistance. How fast is it moving when it hits the ground?
(-81 m/s)
18. Morgan takes the ball and places it at rest, allowing it to roll down an incline that is 3 meters long. It requires 4 seconds to reach the bottom. Find the ball’s (a) speed at the bottom of the incline (b) acceleration (c) displacement between t = 3 s and t = 4 s
(1.5 m/s ; 0.38 m/s2 ; 1.3 m)
19. Nathalia is running at 5 m/s when she accelerates uniformly for 6 seconds, reaching a speed of 15 m/s. Find her (a) acceleration (b) displacement between t = 3 sec and t = 5 sec.
(1.67 m/s2 ; ~ 23 m) 20. Ask Eisner to put up the Roadrunner problem!