Algebra I Final Review 2011
Multiple Choice Identify the letter of the choice that best completes the statement or answers the question.
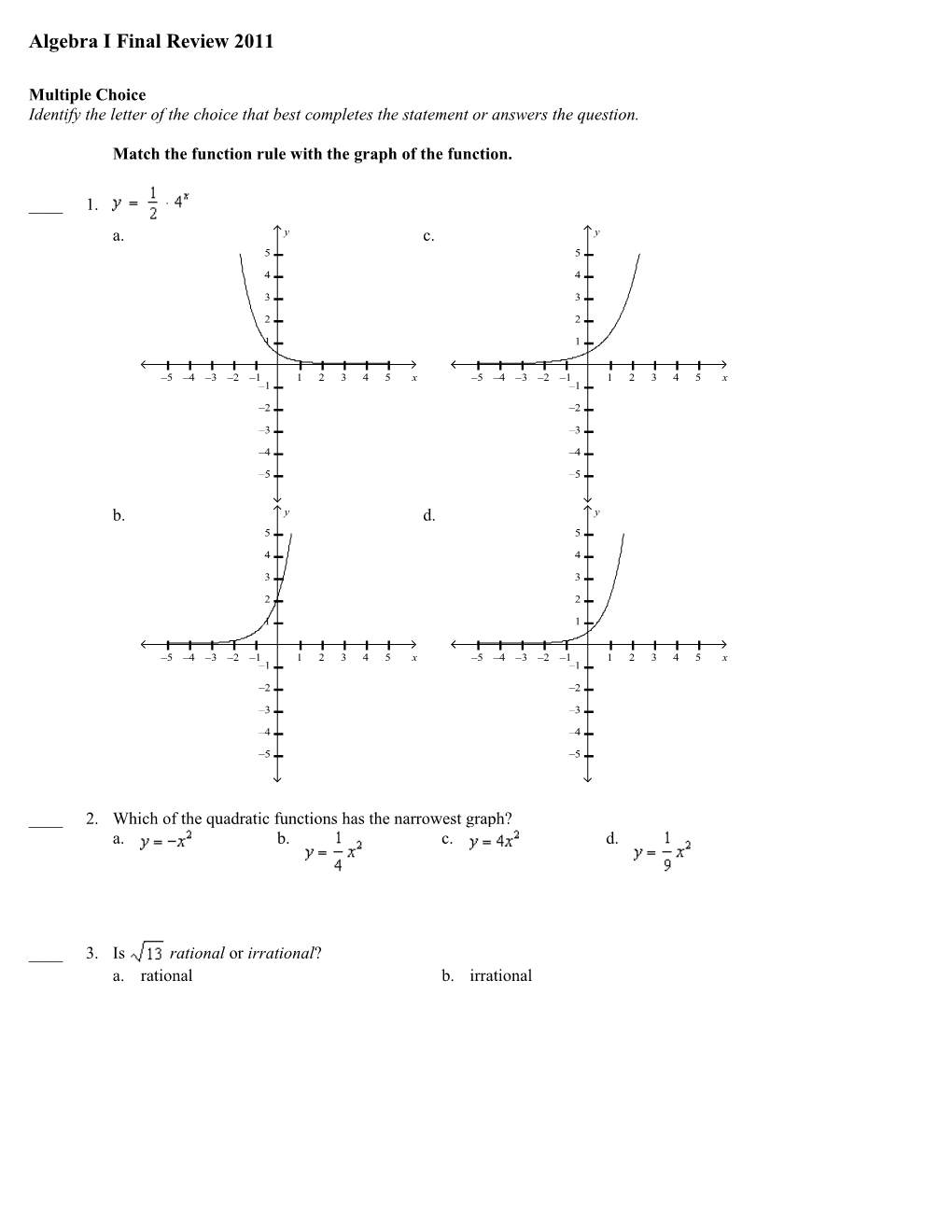
Match the function rule with the graph of the function.
____ 1. a. y c. y 5 5
4 4
3 3
2 2
1 1
–5 –4 –3 –2 –1 1 2 3 4 5 x –5 –4 –3 –2 –1 1 2 3 4 5 x –1 –1
–2 –2
–3 –3
–4 –4
–5 –5
b. y d. y 5 5
4 4
3 3
2 2
1 1
–5 –4 –3 –2 –1 1 2 3 4 5 x –5 –4 –3 –2 –1 1 2 3 4 5 x –1 –1
–2 –2
–3 –3
–4 –4
–5 –5
____ 2. Which of the quadratic functions has the narrowest graph? a. b. c. d.
____ 3. Is rational or irrational? a. rational b. irrational ____ 4. For which discriminant is the graph possible? y 6 4 2
–4 –2 2 4 x –2 –4 –6 –8 –10
a. b. c.
Short Answer
5. Write the polynomial in standard form. 4g – g3 + 3g2 – 2
6. Label by degree and number of terms. 6x3 – 9x + 3
Simplify the difference.
7. (4w2 – 4w – 8) – (2w2 + 3w – 6)
8. Simplify the sum. (4u3 + 4u2 + 2) + (6u3 – 2u + 8)
Simplify the product.
9. 8x2(4x2 + 4y6)
10. 7a3(5a6 – 2b3)
Factor the polynomial.
11. 40w11 + 16w6
12. Find the GCF of the terms of the polynomial. 8x6 + 32x3 13. The Johnsons want to cover their backyard with new grass. Their backyard is rectangular, with a length of 3x – 5 feet and a width of 4x – 10 feet. However, their rectangular swimming pool, along with its surrounding patio, has dimensions of x + 8 by x – 2 feet. What is the area of the region of the yard that they want to cover with new grass?
Simplify.
14.
15.
16. (2n2 + 4n + 4)(4n – 5)
17. (2k + 3)(2k2 – 4k – 3)
Find the square.
18.
Find the product.
19. (4p – 6)(4p + 6)
Complete.
20. z2 + 9z – 90 = (z – 6)(z + )
Factor the expression.
21. d2 + 10d + 9
22. 6x2 + 5x + 1
23.
24. 25. r2 – 49
26. 49b2 – 36
27. Identify the vertex of the graph. Tell whether it is a minimum or maximum. y 4
3
2
1
–4 –3 –2 –1 1 2 3 4 x –1
–2
–3
–4
28. Graph f (x) 2x 2 4x 1. Label the axis of symmetry and vertex.
29. A ball is thrown into the air with an upward velocity of 36 ft/s. Its height h in feet after t seconds is given by the function . a. In how many seconds does the ball reach its maximum height? Round to the nearest hundredth if necessary. b. What is the ball’s maximum height? 30. Simplify .
Solve
31. 7 + 6 = 13
32.
33.
34.
35.
36.
37.
38.
39. Find the number of real number solutions for the equation.
40.
41.
42.
Simplify the radical expression.
43.
44.
45.
46.
47.
Simplify the radical expression by rationalizing the denominator.
48.
49. Simplify the expression.
50.
51.
52. (6 – 11)(6 + 11)
53.
54.
55.
56.
57.
58.
59.
60. 61.
62.
63.
64.
65.
66.
67.
68.
Solve the equation. Check your solution.
69.
70.
71. Solve the equation. Identify any extraneous solutions.
72.
73.
74. Evaluate for x = –3 and y = 2.
Write the number in scientific notation.
75. 8,670,000,000
76. 0.0805
Write the number in standard notation.
77.
78.
Simplify the expression. Write the answer using scientific notation.
79.
Find the common ratio of the sequence.
80. 2, –10, 50, –250, . . .
81. –164, –82, –41, –20.5, . . .
Find the first, fourth, and eighth terms of the sequence.
82. Evaluate the function rule for the given value.
83. for x = –3
84. Suppose a population of 250 crickets doubles in size every 6 months. How many crickets will there be after 2 years?
85. Identify the initial amount a and the growth factor b in the exponential function.
Find the balance in the account.
86. $2,400 principal earning 2%, compounded annually, after 7 years
87. What is the solution of the system of equations? y = 3x + 7 y = x – 9
88. The length of a rectangle is 2 cm more than four times the width. If the perimeter of the rectangle is 84 cm, what are its dimensions?
Solve the system of equations using substitution.
89. y = 2x + 3 y = 3x + 1
90. y = 2x – 10 y = 4x – 8 Solve the system using elimination.
91. 3x + 3y = –9 3x – 3y = 21
92. x + 2y = –6 3x + 8y = –20
93. –10x – 3y = –18 –7x – 8y = 11
94. By what number should you multiply the first equation to solve using elimination? –3x – 2y = 2 –9x + 3y = 24
Graph the inequality.
95. 96.
97.
Write the linear inequality shown in the graph. y
4
2
98. –4 –2 O 2 4 x
–2
–4
Solve the system of linear inequalities by graphing.
99.
Write a system of inequalities for the graph. 100. y 10
8
6
4
2 O –10 –8 –6 –4 –2 2 4 6 8 10 x –2
–4
–6
–8
–10 Algebra I Final Review Answer Section
MULTIPLE CHOICE
1. D 2. C 3. B 4. C
SHORT ANSWER
5. –g3 + 3g2 + 4g – 2 6. cubic trinomial 7. 2w2 – 7w – 2 8. 10u3 + 4u2 – 2u + 10 9. 32x4 + 32x2y6 10. 35a9 – 14a3b3 11. 8w6(5w5 + 2) 12. 8x3 13. 11x2 – 56x + 66 ft2 14. 15. 16. 8n3 + 6n2 – 4n – 20 17. 4k3 – 2k2 – 18k – 9 18. 19. 16p2 – 36 20. 15 21. (d + 9)(d + 1) 22. (3x + 1)(2x + 1) 23. 2(5x – 2)(2x + 3) 24. 25. (r – 7)(r + 7) 26. (7b + 6)(7b – 6) 27. (0, –1); maximum 28. Axis of symmetry: x = 1 Vertex: (1, -7) 29. 1.13 s; 29.25 ft 12 30. 7 31. 32. x = –1 or x = 1 33. z = –3 or z = 9 34. z = 1 or z = –2 35. c = 0 or c = 4
36.
37. 9, 14 38. 1.82, –0.22 39. 0.85, –0.85 40. 2 41. 2 42. 0 43. 44. 12 45.
46.
47. 4 5
48.
49.
50. 51. 52. 25 53. 54. 55. 1 56.
57.
58.
59. 60. 61. 62.
63.
64. 65.
66.
67.
68.
69. 144 70. 116 71. 5 72. 5 is a solution to the original equation. The value –8 is an extraneous solution. 73. 0 and 7 are solutions of the original equation. 1 74. 20 4 75. 76. 77. 90,000 78. 0.0907 79. 6.3 1017 80. –5 81. 82. –2; –16; –256 5 83. 9 84. 4,000 crickets 85. 680, 4.3 86. $2,756.85 87. (–8, –17) 88. length = 34 cm; width = 8 cm 89. (2, 7) 90. (–1, –12) 91. (2, –5) 92. (–4, –1) 93. (3, –4) 94. 3 y
4
2
95. –4 –2 O 2 4 x
–2
–4
y
4
2
96. –4 –2 O 2 4 x
–2
–4 y
4
2
97. –4 –2 O 2 4 x
–2
–4
98. y
4
2
99. –4 –2 O 2 4 x
–2
–4
100.