Phonetic Classification Using Controlled Random Walks
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Thinking in C++ Volume 2 Annotated Solution Guide, Available for a Small Fee From
1 z 516 Note: This document requires the installation of the fonts Georgia, Verdana and Andale Mono (code font) for proper viewing. These can be found at: http://sourceforge.net/project/showfiles.php?group_id=34153&release_id=105355 Revision 19—(August 23, 2003) Finished Chapter 11, which is now going through review and copyediting. Modified a number of examples throughout the book so that they will compile with Linux g++ (basically fixing case- sensitive naming issues). Revision 18—(August 2, 2003) Chapter 5 is complete. Chapter 11 is updated and is near completion. Updated the front matter and index entries. Home stretch now. Revision 17—(July 8, 2003) Chapters 5 and 11 are 90% done! Revision 16—(June 25, 2003) Chapter 5 text is almost complete, but enough is added to justify a separate posting. The example programs for Chapter 11 are also fairly complete. Added a matrix multiplication example to the valarray material in chapter 7. Chapter 7 has been tech-edited. Many corrections due to comments from users have been integrated into the text (thanks!). Revision 15—(March 1 ,2003) Fixed an omission in C10:CuriousSingleton.cpp. Chapters 9 and 10 have been tech-edited. Revision 14—(January ,2003) Fixed a number of fuzzy explanations in response to reader feedback (thanks!). Chapter 9 has been copy-edited. Revision 13—(December 31, 2002) Updated the exercises for Chapter 7. Finished rewriting Chapter 9. Added a template variation of Singleton to chapter 10. Updated the build directives. Fixed lots of stuff. Chapters 5 and 11 still await rewrite. Revision 12—(December 23, 2002) Added material on Design Patterns as Chapter 10 (Concurrency will move to Chapter 11). -

Iterators Must Go
Iterators Must Go Andrei Alexandrescu c 2009 Andrei Alexandrescu 1/52 This Talk • The STL • Iterators • Range-based design • Conclusions c 2009 Andrei Alexandrescu 2/52 What is the STL? c 2009 Andrei Alexandrescu 3/52 Yeah, what is the STL? • A good library of algorithms and data structures. c 2009 Andrei Alexandrescu 4/52 Yeah, what is the STL? • A ( good|bad) library of algorithms and data structures. c 2009 Andrei Alexandrescu 4/52 Yeah, what is the STL? • A ( good|bad|ugly) library of algorithms and data structures. c 2009 Andrei Alexandrescu 4/52 Yeah, what is the STL? • A ( good|bad|ugly) library of algorithms and data structures. • iterators = gcd(containers, algorithms); c 2009 Andrei Alexandrescu 4/52 Yeah, what is the STL? • A ( good|bad|ugly) library of algorithms and data structures. • iterators = gcd(containers, algorithms); • Scrumptious Template Lore • Snout to Tail Length c 2009 Andrei Alexandrescu 4/52 What the STL is • More than the answer, the question is important in the STL • “What would the most general implementations of fundamental containers and algorithms look like?” • Everything else is aftermath • Most importantly: STL is one answer, not the answer c 2009 Andrei Alexandrescu 5/52 STL is nonintuitive c 2009 Andrei Alexandrescu 6/52 STL is nonintuitive • Same way the theory of relativity is nonintuitive • Same way complex numbers are nonintuitive (see e.g. xkcd.com) c 2009 Andrei Alexandrescu 6/52 Nonintuitive • “I want to design the most general algorithms.” • “Sure. What you obviously need is something called iterators. Five of ’em, to be precise.” c 2009 Andrei Alexandrescu 7/52 Nonintuitive • “I want to design the most general algorithms.” • “Sure. -

Peoplesoft Enterprise HRMS 8.9 Application Fundamentals Reports
PeopleSoft Enterprise HRMS 8.9 Application Fundamentals Reports April 2005 PeopleSoft Enterprise HRMS 8.9 Application Fundamentals Reports SKU HRCS89MP1HAF-R 0405 Copyright © 1988-2005 PeopleSoft, Inc. All rights reserved. All material contained in this documentation is proprietary and confidential to PeopleSoft, Inc. (“PeopleSoft”), protected by copyright laws and subject to the nondisclosure provisions of the applicable PeopleSoft agreement. No part of this documentation may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, including, but not limited to, electronic, graphic, mechanical, photocopying, recording, or otherwise without the prior written permission of PeopleSoft. This documentation is subject to change without notice, and PeopleSoft does not warrant that the material contained in this documentation is free of errors. Any errors found in this document should be reported to PeopleSoft in writing. The copyrighted software that accompanies this document is licensed for use only in strict accordance with the applicable license agreement which should be read carefully as it governs the terms of use of the software and this document, including the disclosure thereof. PeopleSoft, PeopleTools, PS/nVision, PeopleCode, PeopleBooks, PeopleTalk, and Vantive are registered trademarks, and Pure Internet Architecture, Intelligent Context Manager, and The Real-Time Enterprise are trademarks of PeopleSoft, Inc. All other company and product names may be trademarks of their respective owners. The information contained herein is subject to change without notice. Open Source Disclosure PeopleSoft takes no responsibility for its use or distribution of any open source or shareware software or documentation and disclaims any and all liability or damages resulting from use of said software or documentation. -

Linux 多线程服务端编程- 使用muduo C++
Linux 多线程服务端编程 使用 muduo C++ 网络库 陈硕 ([email protected]) 最后更新 2012-09-30 封面文案 示范在多核时代采用现代 C++ 编写 多线程 TCP 网络服务器的正规做法 内容简介 本书主要讲述采用现代 C++ 在 x86-64 Linux 上编写多线程 TCP 网络服务程序的 主流常规技术,重点讲解一种适应性较强的多线程服务器的编程模型,即 one loop per thread。这是在 Linux 下以 native 语言编写用户态高性能网络程序最成熟的模 式,掌握之后可顺利地开发各类常见的服务端网络应用程序。本书以 muduo 网络库 为例,讲解这种编程模型的使用方法及注意事项。 本书的宗旨是贵精不贵多。掌握两种基本的同步原语就可以满足各种多线程同步 的功能需求,还能写出更易用的同步设施。掌握一种进程间通信方式和一种多线程网 络编程模型就足以应对日常开发任务,编写运行于公司内网环境的分布式服务系统。 作者简介 陈硕,北京师范大学硕士,擅长 C++ 多线程网络编程和实时分布式系统架构。 曾在摩根士丹利 IT 部门工作 5 年,从事实时外汇交易系统开发。现在在美国加州硅 谷某互联网大公司工作,从事大规模分布式系统的可靠性工程。编写了开源 C++ 网 络库 muduo,参与翻译了《代码大全(第 2 版)》和《C++ 编程规范(繁体版)》,整 理了《C++ Primer (第 4 版)(评注版)》,并曾多次在各地技术大会演讲。 电子工业出版社 封底文案 看完了 W. Richard Stevens 的传世经典《UNIX 网络编程》,能照着例子用 Sockets API 编 写 echo 服务,却仍然对稍微复杂一点的网络编程任务感到无从下手?学习网络编程有哪些好 的练手项目?书中示例代码把业务逻辑和 Sockets 调用混在一起,似乎不利于将来扩展?网络 编程中遇到一些具体问题该怎么办?例如: • 程序在本机测试正常,放到网络上运行就 • 要处理成千上万的并发连接,似乎《UNIX 经常出现数据收不全的情况? 网 络 编 程》 介 绍 的 传 统 fork() 模 型 应 • TCP 协议真的有所谓的“粘包问题”吗? 付不过来,该用哪种并发模型呢?试试 该如何设计消息帧的协议?又该如何编码 select(2)/poll(2)/epoll(4) 这种 IO 复 实现分包才不会掉到陷阱里? 用模型吧,又感觉非阻塞 IO 陷阱重重,怎 • 带外数据(OOB)、信号驱动 IO 这些高级 么程序的 CPU 使用率一直是 100%? 特性到底有没有用? • 要不改用现成的 libevent 网络库吧,怎么 • 网络消息格式该怎么设计?发送 C struct 查询一下数据库就把其他连接上的请求给 会有对齐方面的问题吗?对方不用 C/C++ 耽误了? 怎么通信?将来服务端软件升级,需要在 消息中增加一个字段,现有的客户端就必 • 再用个线程池吧。万一发回响应的时候对 须强制升级? 方已经断开连接了怎么办?会不会串话? 读过《UNIX 环境高级编程》,想用多线程来发挥多核 CPU 的性能潜力,但对程序该用哪 种多线程模型感到一头雾水?有没有值得推荐的适用面广的多线程 IO 模型?互斥器、条件变 量、读写锁、信号量这些底层同步原语哪些该用哪些不该用?有没有更高级的同步设施能简化 开发?《UNIX 网络编程(第 2 卷)》介绍的那些琳琅满目的进程间通信(IPC)机制到底用哪 个才能兼顾开发效率与可伸缩性? 网络编程和多线程编程的基础打得差不多,开始实际做项目了,更多问题扑面而来: • 网上听人说服务端开发要做到 7 × 24 运 • -

Reactive Functional and Imperative C++
Reactive FUNCTIONAL AND IMPERATIVE C++ Ericsson, Budapest 2015 Ivan Cukiˇ ´C KDE University OF Belgrade [email protected] [email protected] Futures The FUNCTIONAL SIDE The IMPERATIVE SIDE Further EVOLUTION OF C++ Epilogue About ME KDE DEVELOPMENT Talks AND TEACHING Functional PROGRAMMING enthusiast, BUT NOT A PURIST 2 Futures The FUNCTIONAL SIDE The IMPERATIVE SIDE Further EVOLUTION OF C++ Epilogue Disclaimer Make YOUR CODE readable. Pretend THE NEXT PERSON WHO LOOKS AT YOUR CODE IS A PSYCHOPATH AND THEY KNOW WHERE YOU live. Philip Wadler 3 Futures The FUNCTIONAL SIDE The IMPERATIVE SIDE Further EVOLUTION OF C++ Epilogue Disclaimer The CODE SNIPPETS ARE OPTIMIZED FOR presentation, IT IS NOT production-ready code. std NAMESPACE IS omitted, VALUE ARGUMENTS USED INSTEAD OF const-refs OR FORWARDING refs, etc. 4 . Futures The FUNCTIONAL SIDE The IMPERATIVE SIDE Further EVOLUTION OF C++ Epilogue Why C++ 6 FUTURES Concurrency Futures Futures The FUNCTIONAL SIDE The IMPERATIVE SIDE Further EVOLUTION OF C++ Epilogue Concurrency Threads Multiple PROCESSES Distributed SYSTEMS Note: "concurrency" WILL MEAN THAT DIffERENT TASKS ARE EXECUTED AT OVERLAPPING times. 8 Futures The FUNCTIONAL SIDE The IMPERATIVE SIDE Further EVOLUTION OF C++ Epilogue Plain THREADS ARE BAD A LARGE FRACTION OF THE flAWS IN SOFTWARE DEVELOPMENT ARE DUE TO PROGRAMMERS NOT FULLY UNDERSTANDING ALL THE POSSIBLE STATES THEIR CODE MAY EXECUTE in. In A MULTITHREADED environment, THE LACK OF UNDERSTANDING AND THE RESULTING PROBLEMS ARE GREATLY AMPLIfiED, ALMOST TO THE POINT OF PANIC IF YOU ARE PAYING attention. John Carmack In-depth: Functional PROGRAMMING IN C++ 9 Futures The FUNCTIONAL SIDE The IMPERATIVE SIDE Further EVOLUTION OF C++ Epilogue Plain THREADS ARE BAD Threads ARE NOT COMPOSABLE Parallelism CAN’T BE ‘DISABLED’ DiffiCULT TO ENSURE BALANCED LOAD MANUALLY Hartmut Kaiser Plain Threads ARE THE GOTO OF Today’S Computing 10 Futures The FUNCTIONAL SIDE The IMPERATIVE SIDE Further EVOLUTION OF C++ Epilogue Plain SYNCHRONIZATION PRIMITIVES ARE BAD You WILL LIKELY GET IT WRONG S.L.O.W. -

D Programming Language: the Sudden
D Programming Language: The Sudden Andrei Alexandrescu, Ph.D. Research Scientist, Facebook [email protected] YOW 2014 c 2014– Andrei Alexandrescu. 1/44 Introduction c 2014– Andrei Alexandrescu. 2/44 Introduction c 2014– Andrei Alexandrescu. 3/44 Sudden Sequels • Pronouncing “Melbourne” and “Brisbane” c 2014– Andrei Alexandrescu. 4/44 Sudden Sequels • Pronouncing “Melbourne” and “Brisbane” • Burn Identity c 2014– Andrei Alexandrescu. 4/44 Sudden Sequels • Pronouncing “Melbourne” and “Brisbane” • Burn Identity Sequel to Bourne Identity and Burn Notice c 2014– Andrei Alexandrescu. 4/44 Sudden Sequels • Pronouncing “Melbourne” and “Brisbane” • Burn Identity Sequel to Bourne Identity and Burn Notice • Airburn Infantry c 2014– Andrei Alexandrescu. 4/44 Sudden Sequels • Pronouncing “Melbourne” and “Brisbane” • Burn Identity Sequel to Bourne Identity and Burn Notice • Airburn Infantry Sequel to BoB and Operation Flamethrower c 2014– Andrei Alexandrescu. 4/44 Sudden Sequels • Pronouncing “Melbourne” and “Brisbane” • Burn Identity Sequel to Bourne Identity and Burn Notice • Airburn Infantry Sequel to BoB and Operation Flamethrower • Newburn c 2014– Andrei Alexandrescu. 4/44 Sudden Sequels • Pronouncing “Melbourne” and “Brisbane” • Burn Identity Sequel to Bourne Identity and Burn Notice • Airburn Infantry Sequel to BoB and Operation Flamethrower • Newburn Sequel to Chucky and Spontaneous Combustion c 2014– Andrei Alexandrescu. 4/44 Sudden Sequels • Pronouncing “Melbourne” and “Brisbane” • Burn Identity Sequel to Bourne Identity and Burn Notice • Airburn Infantry Sequel to BoB and Operation Flamethrower • Newburn Sequel to Chucky and Spontaneous Combustion • The Dark Knight Rises c 2014– Andrei Alexandrescu. 4/44 Sudden Sequels • Pronouncing “Melbourne” and “Brisbane” • Burn Identity Sequel to Bourne Identity and Burn Notice • Airburn Infantry Sequel to BoB and Operation Flamethrower • Newburn Sequel to Chucky and Spontaneous Combustion • The Dark Knight Rises Batman vs. -

Nim - the First High Performance Language with Full Support for Hot Code- Reloading at Runtime
Nim - the first high performance language with full support for hot code- reloading at runtime by Viktor Kirilov 1 Me, myself and I my name is Viktor Kirilov - from Bulgaria creator of doctest - the fastest C++ testing framework apparently I like text-heavy slides and reading from them...! deal with it :| 2 Talk agenda some Nim code the performant programming language landscape read: heavily biased C++ rant Nim compilation model hot code reloading usage & implementation ".dll" => assume .so/.dylib (platform-agnostic) demo comments & conclusions a bit on REPLs 3 Hello 1 echo "Hello World" 4 Currencies 1 type 2 # or use {.borrow.} here to inherit everything 3 Dollars* = distinct float 4 5 proc `+` *(a, b: Dollars): Dollars {.borrow.} 6 7 var a = 20.Dollars 8 9 a = 25 # Doesn't compile 10 a = 25.Dollars # Works fine 11 12 a = 20.Dollars * 20.Dollars # Doesn't compile 13 a = 20.Dollars + 20.Dollars # Works fine 5 Sets 6 Iterators 1 type 2 CustomRange = object 3 low: int 4 high: int 5 6 iterator items(range: CustomRange): int = 7 var i = range.low 8 while i <= range.high: 9 yield i 10 inc i 11 12 iterator pairs(range: CustomRange): tuple[a: int, b: char] = 13 for i in range: # uses CustomRange.items 14 yield (i, char(i + ord('a'))) 15 16 for i, c in CustomRange(low: 1, high: 3): 17 echo c 18 19 # prints: b, c, d 7 Variants 1 # This is an example how an abstract syntax tree could be modelled in Nim 2 type 3 NodeKind = enum # the different node types 4 nkInt, # a leaf with an integer value 5 nkFloat, # a leaf with a float value 6 nkString, # -
C++ Developer Survey "Lite": 2018-02
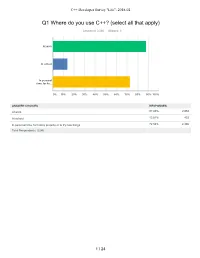
C++ Developer Survey "Lite": 2018-02 Q1 Where do you use C++? (select all that apply) Answered: 3,280 Skipped: 6 At work At school In personal time, for ho... 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ANSWER CHOICES RESPONSES At work 87.93% 2,884 At school 13.81% 453 In personal time, for hobby projects or to try new things 72.56% 2,380 Total Respondents: 3,280 1 / 24 C++ Developer Survey "Lite": 2018-02 Q2 How many years of programming experience do you have in C++ specifically? Answered: 3,271 Skipped: 15 1-2 years 3-5 years 6-10 years 10-20 years >20 years 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ANSWER CHOICES RESPONSES 1-2 years 10.27% 336 3-5 years 20.85% 682 6-10 years 22.87% 748 10-20 years 30.63% 1,002 >20 years 15.38% 503 TOTAL 3,271 2 / 24 C++ Developer Survey "Lite": 2018-02 Q3 How many years of programming experience do you have overall (all languages)? Answered: 3,276 Skipped: 10 1-2 years 3-5 years 6-10 years 10-20 years >20 years 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ANSWER CHOICES RESPONSES 1-2 years 2.26% 74 3-5 years 11.66% 382 6-10 years 23.78% 779 10-20 years 33.55% 1,099 >20 years 28.75% 942 TOTAL 3,276 3 / 24 C++ Developer Survey "Lite": 2018-02 Q4 What types of projects do you work on? (select all that apply) Answered: 3,269 Skipped: 17 Business (e.g., B2B,.. -

Static If I Had a Hammer
Static If I Had a Hammer Andrei Alexandrescu Research Scientist Facebook c 2012– Andrei Alexandrescu, Facebook. 1/27 In a nutshell (1/2) enum class WithParent { no, yes }; template <class T, WithParent wp> class Tree { class Node { ... }; static if (wp == WithParent::yes) { Node * parent_; } Node * left_, * right_; T payload_; ::: }; Tree<string, WithParent::yes> dictionary; c 2012– Andrei Alexandrescu, Facebook. 2/27 In a nutshell (2/2) template <class It> It rotate(It b, It m, It e) if (is_forward_iterator<It>::value) { ::: } c 2012– Andrei Alexandrescu, Facebook. 3/27 Agenda • Motivation • The static if declaration • Template constraints • Implementation issues c 2012– Andrei Alexandrescu, Facebook. 4/27 • In a nutshell (1/2) • In a nutshell (2/2) • Agenda Motivation • Why static if? • Why not static if? • A non-starter: #if The static if declaration Template Constraints Motivation Implementation Issues Time for ritual speakercide c 2012– Andrei Alexandrescu, Facebook. 5/27 Why static if? • Introspection-driven code ◦ Acknowledged, encouraged: <traits> ◦ Incomplete: no trait-driven conditional compilation • Recursive templates impose signature duplication • Specialization on arbitrary type properties ◦ enable_if incomplete, syntax-heavy, has corner cases • Difficulty in defining policy-based designs • Opportunistic optimizations depending on type properties c 2012– Andrei Alexandrescu, Facebook. 6/27 Why not static if? • Would you define a new function for every if? • Makes advanced libraries ◦ Easy to implement and debug ◦ Easy to understand and use • Simple problems should have simple solutions ◦ “This function only works with numbers” ◦ “This algorithm requires forward iterators” ◦ “I can choose whether this tree has parent pointers” c 2012– Andrei Alexandrescu, Facebook. 7/27 A non-starter: #if • “Conditional compilation” associated with preprocessor • Preprocessing step long before semantic analysis • Poor integration with the language • Impossible to test any trait ◦ Or really anything interesting c 2012– Andrei Alexandrescu, Facebook. -
Dr. Sumant Tambe Dr. Aniruddha Gokhale Software Engineer Associate Professor of EECS Dept
LEESA: Toward Native XML Processing Using Multi-paradigm Design in C++ May 16, 2011 Dr. Sumant Tambe Dr. Aniruddha Gokhale Software Engineer Associate Professor of EECS Dept. Real-Time Innovations Vanderbilt University www.dre.vanderbilt.edu/LEESA 1 / 54 . XML Programming in C++. Specifically, data binding . What XML data binding stole from us! . Restoring order: LEESA . LEESA by examples . LEESA in detail . Architecture of LEESA . Type-driven data access . XML schema representation using Boost.MPL . LEESA descendant axis and strategic programming . Compile-time schema conformance checking . LEESA expression templates . Evaluation: productivity, performance, compilers . C++0x and LEESA . LEESA in future 2 / 54 XML Infoset Cɷ 3 / 54 . Type system . Regular types . Anonymous complex elements . Repeating subsequence . XML data model . XML information set (infoset) . E.g., Elements, attributes, text, comments, processing instructions, namespaces, etc. etc. Schema languages . XSD, DTD, RELAX NG . Programming Languages . XPath, XQuery, XSLT . Idioms and best practices . XPath: Child, parent, sibling, descendant axes; wildcards 4 / 54 . Predominant categories & examples (non-exhaustive) . DOM API . Apache Xerces-C++, RapidXML, Tinyxml, Libxml2, PugiXML, lxml, Arabica, MSXML, and many more … . Event-driven APIs (SAX and SAX-like) . Apache SAX API for C++, Expat, Arabica, MSXML, CodeSynthesis XSD/e, and many more … . XML data binding . Liquid XML Studio, Code Synthesis XSD, Codalogic LMX, xmlplus, OSS XSD, XBinder, and many more … . Boost XML?? . No XML library in Boost (as of May 16, 2011) . Issues: very broad requirements, large XML specifications, good XML libraries exist already, encoding issues, round tripping issues, and more … 5 / 54 XML query/traversal program XML Schema Uses XML Schema Object-oriented C++ Generate i/p Generate Executable i/p Compiler Data Access Layer Compiler (Code Generator) C++ Code . -

Three Cool Things About D
Three Cool Things About D Andrei Alexandrescu Research Scientist Facebook c 2010 Andrei Alexandrescu 1/47 What’s the Deal? c 2010 Andrei Alexandrescu 2/47 PL Landscape • Systems/Productivity languages • Imperative/Declarative/Functional languages • nth generation languages • Compiled/Interpreted/JITed languages • . c 2010 Andrei Alexandrescu 3/47 Sahara • Sahara-sized desert around the crossroads of ◦ High efficiency ◦ Systems-level access ◦ Modeling power ◦ Simplicity ◦ High productivity ◦ Code correctness (of parallel programs, too) c 2010 Andrei Alexandrescu 4/47 Sahara • Sahara-sized desert around the crossroads of ◦ High efficiency ◦ Systems-level access ◦ Modeling power ◦ Simplicity ◦ High productivity ◦ Code correctness (of parallel programs, too) • Traditionally: focus on a couple and try to keep others under control c 2010 Andrei Alexandrescu 4/47 Sahara • Sahara-sized desert around the crossroads of ◦ High efficiency ◦ Systems-level access ◦ Modeling power ◦ Simplicity ◦ High productivity ◦ Code correctness (of parallel programs, too) • Traditionally: focus on a couple and try to keep others under control • C++: ruler of 1-2, strong on 3, goes south after that c 2010 Andrei Alexandrescu 4/47 Sahara • Sahara-sized desert around the crossroads of ◦ High efficiency ◦ Systems-level access ◦ Modeling power ◦ Simplicity ◦ High productivity ◦ Code correctness (of parallel programs, too) • Traditionally: focus on a couple and try to keep others under control • C++: ruler of 1-2, strong on 3, goes south after that • D: holistic approach -

Lock-Free Data Structures
Lock-Free Data Structures Andrei Alexandrescu December 17, 2007 After GenerichProgrammingi has skipped one in- operations that change data must appear as atomic stance (it’s quite na¨ıve, I know, to think that grad such that no other thread intervenes to spoil your school asks for anything less than 100% of one’s data’s invariant. Even a simple operation such as time), there has been an embarrassment of riches as ++count_, where count_ is an integral type, must be far as topic candidates for this article go. One topic locked as “++” is really a three steps (read, modify, candidate was a discussion of constructors, in par- write) operation that isn’t necessarily atomic. ticular forwarding constructors, handling exceptions, In short, with lock-based multithreaded program- and two-stage object construction. One other topic ming, you need to make sure that any operation on candidate—and another glimpse into the Yaslander shared data that is susceptible to race conditions is technology [2]—was creating containers (such as lists, made atomic by locking and unlocking a mutex. On vectors, or maps) of incomplete types, something that the bright side, as long as the mutex is locked, you is possible with the help of an interesting set of tricks, can perform just about any operation, in confidence but not guaranteed by the standard containers. that no other thread will trump on your shared state. While both candidates were interesting, they It is exactly this “arbitrary”-ness of what you can couldn’t stand a chance against lock-free data struc- do while a mutex is locked that’s also problematic.