Write Your Response Here: (Show Your Work)

Coordinate Geometry 1. Three vertices of isosceles trapezoid JKLM are located at J(5,0), K(-4,0), and L(- 2,-5), with JK representing one of the bases. Use the distance formula to find the location of point M.

A. (3,0) B. (5,-5) C. (7,-5) D. (3,-5) 2.

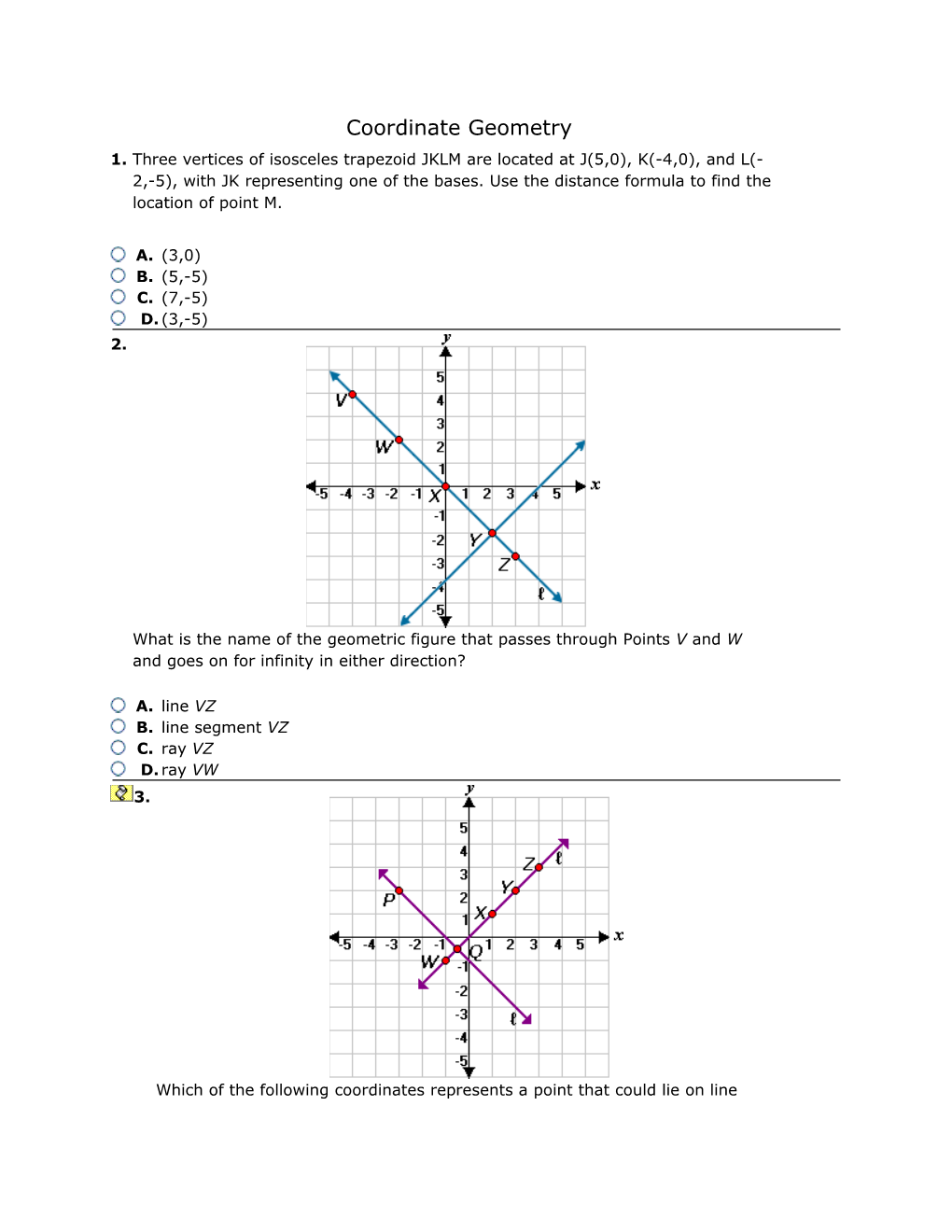
What is the name of the geometric figure that passes through Points V and W and goes on for infinity in either direction?

A. line VZ B. line segment VZ C. ray VZ D. ray VW 3.

Which of the following coordinates represents a point that could lie on line segment PQ?

1 -3 A. ( /2, /2) -9 7 B. ( /2, /2) -7 5 C. ( /2, /2) -3 1 D. ( /2, /2) 4.

A. B. C. D. 5. Two vertices of square QRST are located at Q(-1,-1) and R(1,3). Use the distance formula to find the locations of point S and point T.

A. S(5,1) and T(3,-3) B. S(5,0) and T(3,-4) C. S(7,0) and T(5,-4) D. S(3,2) and T(1,-2) 6. The vertices of a quadrilateral are listed below.

L(6,2), M(13,-5), N(6,-12), O(-1,-5) Which of the following is the strongest classification that identifies this quadrilateral?

A. The quadrilateral is a trapezoid. B. The quadrilateral is a rhombus. C. The quadrilateral is a rectangle. D. The quadrilateral is a square. 7.

What is the name of the geometric figure that begins at point V, passes through point W, and goes on for infinity in one direction? A. line VW B. point VW C. line segment VW D. ray VW 8.

Which of these coordinates represents the point M so that M is the midpoint of line segment AB?

A. (1, 2) B. (2, 2) C. (0, -1) D. (2, 1) 9. Point Y lies on Line WZ. Which of the following coordinates represents a point that also lies on line WZ?

A. (-22,22) B. (0,1) C. (-22,-22) D. (22,-22) 10.

Which of the following coordinates represents a point that lies on ray PQ?

A. (-5,6) B. (-5,4) C. (15,-14) D. (15,-16) 11. The vertices of a quadrilateral are listed below.

Q(-2,7), R(5,7), S(4,-4), T(-3,-4) Which of the following is the strongest classification that identifies this quadrilateral?

A. The quadrilateral is a rhombus. B. The quadrilateral is a rectangle. C. The quadrilateral is a parallelogram. D. The quadrilateral is a square. 12. The vertices of square EFGH are located at E(-5,4), F(1,7), G(4,1), and H(-2,-2). If square JKLM is inscribed inside square EFGH at its midpoints, which of the following is the slope of one of the sides of square JKLM?

A. B. C. D. 13. The base of isosceles triangle QRS has endpoints at Q(-1,3) and R(3,-5). If sides QS and RS have a length of , what is the location of point S?

A. (6,-1) B. (-5,-6) C. (-3,-3) D. (-5,-4) 14.

15. The vertices of a triangle are listed below.

H(-9,7), I(39,7), J(15,-3) Which of the following correctly classifies the triangle?

A. The triangle is an acute isosceles triangle. B. The triangle is an obtuse isosceles triangle. C. The triangle is an obtuse scalene triangle. D. The triangle is an acute equilateral triangle. 16. The vertices of a quadrilateral are listed below.

A(7,-4), B(13,-4), C(17,-8), D(7,-8) Which of the following is the strongest classification that identifies this quadrilateral?

A. The quadrilateral is a trapezoid. B. The quadrilateral is a square. C. The quadrilateral is a rectangle. D. The quadrilateral is a rhombus. 17.

Which of these coordinates represents the point M so that M is the intersection of the diagonals of the given parallelogram?

A. (-1, -2) B. (1, -2) C. (1, 2) D. (-2, -1) 18. Which of these coordinates represents the endpoint of a midsegment of the given triangle?

A. (-3, 1) B. (-2, 1) C. (-2, 2) D. (2, 2) 19.

Which of these coordinates represents the point B so that line AB is parallel to the given line?

A. (6, 3) B. (7, 3) C. (3, 7) D. (3, 6) 20.

What is the name of the geometric figure that begins at point V and ends at point X?

A. line VX B. point VX C. line segment VX D. ray VX 21.

Which point lies on line PQ?

A. Y B. P C. W D. Z 22.

23. The vertices of a quadrilateral are listed below.

E(3,2), F(7,0), G(3,-2), H(-1,0) Which of the following is the strongest classification that identifies this quadrilateral?

A. The quadrilateral is a rhombus. B. The quadrilateral is a rectangle. C. The quadrilateral is a trapezoid. D. The quadrilateral is a square. 24. The vertices of a quadrilateral are listed below.

E(2,3), F(6,1), G(2,-1), H(-2,1) Which of the following is the strongest classification that identifies this quadrilateral?

A. The quadrilateral is a rectangle. B. The quadrilateral is a trapezoid. C. The quadrilateral is a square. D. The quadrilateral is a rhombus. 25. Which of the following equations represents a line which is perpendicular to the line that passes through the points below?

B. C. D. 26.

Which of these coordinates represents the point D so that ray CD is perpendicular to line segment AB?

A. (6,7) B. (1,2) C. (7,7) D. (5,4) 27. The vertices of a triangle are listed below.

W(5,5), X(2,-6), Y(-1,-4) Which of the following correctly classifies the triangle?

A. The triangle is a right isosceles triangle. B. The triangle is an obtuse isosceles triangle. C. The triangle is a right scalene triangle. D. The triangle is an acute equilateral triangle. 28. Which of the following equations represents a line which is perpendicular to the line that passes through the points below?

C. D. 29. The vertices of a quadrilateral are listed below.

W(7,5), X(10,3), Y(4,-6), Z(1,-4) Which of the following is the strongest classification that identifies this quadrilateral?

A. The quadrilateral is a square. B. The quadrilateral is a rectangle. C. The quadrilateral is a trapezoid. D. The quadrilateral is a rhombus. 30. Which of the following equations represents a line which is parallel to the line that passes through the points below?

A. B. C.

31. The vertices of a triangle are listed below.

A(-8,3), B(-20,-6), C(-8,-15) Which of the following correctly classifies the triangle?

A. The triangle is an obtuse isosceles triangle. B. The triangle is an acute scalene triangle. C. The triangle is an acute isosceles triangle. D. The triangle is an obtuse scalene triangle. 32. The vertices of a triangle are listed below.

E(4,7), F(9,5), G(4,1) Which of the following correctly classifies the triangle?

A. The triangle is a right isosceles triangle. B. The triangle is an obtuse scalene triangle. C. The triangle is an acute equilateral triangle. D. The triangle is an acute scalene triangle. 33.

Which of these coordinates represents the point C so that C is the center of the circle?

A. (3, -1) B. (-1, 3) C. (-2, 3) D. (-1, 2) 34. If two vertices of quadrilateral QRST are located at Q(-5,2) and R(1,4), which of the following pair of vertices would make a square?

A. S(2,1) and T(-4,-1) B. S(1,-1) and T(-5,-3) C. S(3,-2) and T(-3,-4) D. S(5,2) and T(-4,-1) 35. The vertices of a triangle are listed below.

Q(-4,5), R(7,5), S(-7,-4) Which of the following correctly classifies the triangle?

A. The triangle is an acute scalene triangle. B. The triangle is a right scalene triangle. C. The triangle is an obtuse scalene triangle. D. The triangle is an acute equilateral triangle. 36. The vertices of a triangle are listed below.

L(2,2), M(9,-5), N(2,-12) Which of the following correctly classifies the triangle?

A. The triangle is an acute scalene triangle. B. The triangle is an obtuse scalene triangle. C. The triangle is a right isosceles triangle. D. The triangle is a right scalene triangle. 37. Three vertices of isosceles trapezoid JKLM are located at J(-3,0), K(-3,3), and L(1,5), with JK representing one of the bases. Use the distance formula to find the location of point M.

A. (1,-1) B. (1,-2) C. (1,-3) D. (1,-4) 38. Which of the following equations represents a line which is parallel to the line that passes through the points below?

C. D. 39.

A. B. C. D.

What is the geometric term for the figure that is represented by the dot labeled Z?

A. ray B. point C. line D. line segment

Answers 1. D 2. A 3. D 4. A 5. A 6. D 7. D 8. D 9. C 10. D 11. C 12. D 13. D 14. D 15. B 16. A 17. A 18. C 19. C 20. C 21. B 22. D 23. A 24. D 25. A 26. C 27. C 28. C 29. B 30. A 31. C 32. D 33. B 34. C 35. C 36. C 37. B 38. A 39. B 40. B

Explanations

1. A trapezoid is a quadrilateral that contains one pair of parallel sides and one pair of non-parallel sides. The parallel sides are called the bases.

Since JK is one of the bases, it will be parallel to LM. Since the points for J and K have the same y-coordinate, JK is a horizontal line segment.

Therefore, point L will have the same y-coordinate as point M, and LM will also be horizontal.

Since trapezoid JKLM is isosceles, its two non-parallel sides, JM and KL, must have equal lengths. Find the length of KL, which is the distance between K(-4,0) and L(- 2,-5).

Find M(x,y) such that the distance to J(5,0) is .

Thus, the fourth vertex of the isosceles trapezoid is M(3,-5).

2. A point is a single location on a line. Rays extend from one point and go on for infinity in one direction. Line segments are parts of lines that extend from one endpoint to the other. Lines goes on for infinity in either direction, so the answer is line VZ.

3. Find the slope of line PQ.

Use the coordinates (-3,2) for x2 and y2. Use the coordinates (-1,0) for x1 and y1.

y2 - y1 2 - 0 = m = = x2 - x1 -3 - (-1) -1 The y-intercept is -1, so the equation of the line is y = -x - 1. Plug in the x- coordinates given.

y = -x - 1 x y

-9 7 /2 /2

-7 5 /2 /2

-3 1 /2 /2 0 -1

1 -3 /2 /2 -3 1 Of all the coordinates given, only the point represented by coordinates ( /2, /2) lies on line segment PQ, since the line segment PQ must start at point P and end at point Q.

5. A square is a parallelogram with four right angles and four congruent sides.

Find the slope of each side for each pair of vertices. Slope Slope Slope Slope of QR of RS of ST of TQ S(7,0)

T(5,-4) S(3,2)

T(1,-2) S(5,0)

T(3,-4) S(5,1)

T(3,-3)

Side QR is opposite side ST and side RS is opposite side TQ. If opposite sides have the same slope, then they are parallel. Therefore, all the quadrilaterals listed above are parallelograms.

If adjacent sides have slopes that are opposite sign reciprocals, then they are perpendicular. Therefore, all quadrilaterals listed above, except the third one, have four right angles.

To determine which of the three parallelograms with four right angles in the table above is a square, calculate the length of two adjacent sides for the three pairs of vertices. Length of QR Length of RS S(7,0) T(5,-4) S(3,2) T(1,-2) S(5,1) T(3,-3)

Since the last pair of vertices from the above table have adjacent sides that are congruent, then the quadrilateral is a square.

Thus, vertices S(5,1) and T(3,-3) make a square when paired with Q(-1,-1) and R(1,3).

6. Find the slope of each side of the quadrilateral.

Since opposite sides have equal slopes, the opposite sides are parallel. So, the shape is not a trapezoid. Since adjacent sides have slopes that are negative reciprocals, the sides are perpendicular. So, the shape is either a rectangle or a square.

Find the length of two adjacent sides.

Since the two adjacent sides are equal, the quadrilateral is a square.

7. A point is a single location on a line. Line segments extend from one point to another on a line, and have two endpoints. Lines go on for infinity in either direction.

Rays extend from one point and go on for infinity in one direction, so the answer is ray VW.

8. The midpoint of a segment is the point that divides the segment into two congruent segments.

Since the slope of the graphed line is equal to 1, each diagonal distance in a grid square can be counted between the points. There are 12 diagonal lengths. After counting 6 of these lengths going from one point to the other point, it can be seen that the midpoint is at (2, 1).

Therefore, the coordinate which represents the point M so that M is the midpoint of line segment AB is (2, 1). 9. Find the slope of the line. Use Point Z, (3,3), for x2 and y2. Use Point Y, (2,2), for x1

and y1.

y2 - y1 3 - 2 = m = = x2 - x1 3 - 2 1 The y-intercept is 0, so the equation of the line is y = x. Plug in the x coordinates given.

y = x x y -22 -22 0 0 22 22 Only the point represented by coordinates (-22,-22) lies on Line WZ.

10. Find the slope of line PQ. Use the coordinates (-3,2) for x2 and y2. Use the

coordinates (-1,0) for x1 and y1.

y2 - y1 2 - 0 = m = = x2 - x1 -3 - (-1) -1 The y-intercept is -1, so the equation of the line is y = -x - 1. Plug in the x coordinates given.

y = -x - 1 x y -5 4 0 -1 15 -16 The point that has the coordinates (-5,4), lies on line PQ, but not ray PQ, since ray PQ starts at point P and continues in the direction of point Q.

The only coordinates given that represent a point that lies on ray PQ are (15,-16).

Since opposite sides have equal slopes, the opposite sides are parallel.

Since adjacent sides do not have negative reciprocal slopes, the sides are not perpendicular. So, the shape is not a rectangle or a square. Find the length of two adjacent sides.

Since the two adjacent sides are not equal, the shape is not a rhombus.

Therefore, the quadrilateral is a parallelogram.

12. Since square JKLM is inscribed inside square EFGH at its midpoints, first find the midpoint of each side of square EFGH.

E(-5,4) F(1,7) G(4,1) H(-2,-2) Endpoints F(1,7) G(4,1) H(-2,-2) E(-5,4)

Calc. x-value -5 + 1 1 + 4 4 + (-2) -2 + (-5) of Midpoint 2 2 2 2

Calc. y-value 4 + 7 7 + 1 1 + (-2) -2 + 4 of Midpoint 2 2 2 2

Midpoint (-2,5.5) (2.5,4) (1,-0.5) (-3.5,1)

To find the slopes of the sides of square JKLM, determine the slope between the midpoints in the table above.

Since a square's opposite sides are parallel, it is only necessary to calculate the slope of two adjacent sides.

Calculate Slope Calculate Slope between between (-2,5.5) and (2.5,4) (2.5,4) and (1,-0.5) 4 - 5.5 -0.5 - 4 2.5 - (-2) 1 - 2.5

Thus, the sides of square JKLM have a slope of either or .

13. Use the distance formula to find point S such that sides QS and RS both have a length of .

First, find the length of QS for each answer choice.

Point Q Point S Calculate the Length of QS

(-1,3) (6,-1)

(-1,3) (-5,-6)

(-1,3) (-3,-3)

(-1,3) (-5,-4)

Next, find the length of RS for each answer choice.

Point R Point S Calculate the Length of RS

(3,-5) (6,-1)

(3,-5) (-5,-6)

(3,-5) (-3,-3)

(3,-5) (-5,-4) The only location for S that gives a length of for both QS and RS is (-5,-4).

15. Use the distance formula to find the length of each side of the triangle.

Since two sides have the same length, the triangle is isosceles. Where a, b, and c are the lengths of the sides and c is the longest side, if c2 < a2 + b2, then it is an acute triangle, if c2 = a2 + b2, then it is a right triangle, and if c2 > a2 + b2, then it is an obtuse triangle.

Since the square of the longest side is greater than the sum of the squares of the other two sides, the triangle is obtuse.

Therefore, the triangle is an obtuse isosceles triangle.

The two sides that have a slope of zero are horizontal. The side that has an undefined slope is vertical. So, this shape has only one pair of opposite sides that are parallel.

Therefore, the quadrilateral is a trapezoid. 17. The intersection of the diagonals of the given parallelogram is shown in the following figure.

Therefore, the coordinate that represents the point M so that M is the intersection of the diagonals of the given parallelogram is (-1, -2).

18. A midsegment of a triangle is a line segment connecting the midpoint of two sides and that is parallel to the third side. The midpoint of the line segments in the given triangle are shown in the following figure. As seen in the figure, the midpoint of AC, M1, is (-2, 2).

Therefore, the coordinate that represents the endpoint of a midsegment is (-2, 2).

19. Consider the answer choices (6, 3) and (7, 3). Locate these choices on the grid, and consider the possible lines that can be formed with the point A when either of these points is equal to B. It can be seen without calculating the slope that neither point will form a line with point A that is parallel to the given line.

Next, consider the points (3, 6) and (3, 7) and the lines that they would form with the point A. Without calculating the slope, it can be seen that both points could indeed form a line with A that is parallel with the given line.

To determine the correct point, calculate the slope of the given line and the slopes of the lines that can be formed with the point A and the points (3, 6) and (3, 7). To calculate the slope of the given line, the x- and y-intercept, (3, 0) and (0, -3), will be used. Therefore, the coordinate that represents the point B so that line segment AB is parallel to the given line is (3, 7).

20. A point is a single location on a line. A line goes on for infinity in either direction. A ray extends from one point and go on for infinity in one direction.

A line segment is a piece of a line that extends from one endpoint to the other. Therefore, the answer is line segment VX.

21. Points Q, W, X, Y, and Z all lie on line WZ.

Points P and Q are on line PQ.

Therefore, point P is on line line PQ.

Since opposite sides have equal slopes, the opposite sides are parallel. So, the shape is not a trapezoid. Since adjacent sides do not have negative reciprocal slopes, the sides are not perpendicular. So, the shape is not a rectangle or a square.

Since the two adjacent sides are equal, the quadrilateral is a rhombus.

Since opposite sides have equal slopes, the opposite sides are parallel. So, the shape is not a trapezoid.

Since adjacent sides do not have negative reciprocal slopes, the sides are not perpendicular. So, the shape is not a rectangle or a square.

Since the two adjacent sides are equal, the quadrilateral is a rhombus.

25. The slopes of two perpendicular lines are negative reciprocals of one another. To find the correct line, calculate the slope of the line which passes through the given points.

Therefore, the line which passes through the given points is perpendicular to

26. Ray CD must be perpendicular to the line segment AB. The line segment AB has a slope of -1, so the slope of ray CD must be 1. Using the slope to draw a ray extending from the point C, it can be seen that the only point given which lies on the ray is (7,7). Ray CD is shown in the following figure. Therefore, the coordinate that represents the point D so that ray CD is perpendicular to line segment AB is (7, 7).

Since the three sides all have different lengths, the triangle is scalene. Where a, b, and c are the lengths of the sides and c is the longest side, if c2 < a2 + b2, then it is an acute triangle, if c2 = a2 + b2, then it is a right triangle, and if c2 > a2 + b2, then it is an obtuse triangle.

Since the square of the longest side is equal to the sum of the squares of the other two sides, the triangle is right.

Therefore, the triangle is a right scalene triangle.

28. The slopes of two perpendicular lines are negative reciprocals of one another. To find the correct line, calculate the slope of the line which passes through the given points.

Therefore, the line which passes through the given points is perpendicular to 29. Find the slope of each side of the quadrilateral.

Since opposite sides have equal slopes, the opposite sides are parallel. So, the shape is not a trapezoid.

Since adjacent sides have slopes that are negative reciprocals, the sides are perpendicular. So, the shape is either a rectangle or a square.

Since the two adjacent sides are not equal, the shape is not a square.

Therefore, the quadrilateral is a rectangle.

30. Parallel lines have the same slope, so to find the correct line, calculate the slope of the line which passes through the given points.

Therefore, the line which passes through the given points is parallel to .

Since the square of the longest side is less than the sum of the squares of the other two sides, the triangle is acute.

Therefore, the triangle is an acute isosceles triangle.

32. Use the distance formula to find the length of each side of the triangle. Since the three sides all have different lengths, the triangle is scalene. Where a, b, and c are the lengths of the sides and c is the longest side, if c2 < a2 + b2, then it is an acute triangle, if c2 = a2 + b2, then it is a right triangle, and if c2 > a2 + b2, then it is an obtuse triangle.

Since the square of the longest side is less than the sum of the squares of the other two sides, the triangle is acute.

Therefore, the triangle is an acute scalene triangle.

33. A circle is the collection of all points in a plane that are equidistant from a given point or the center of a circle, C.

A line connecting the points (-6, 3) and (4, 3) forms a diameter of the circle. Thus, the diameter is equal to 10 units. Count 5 units from either point toward the center of the circle to arrive at the point (-1, 3).

The circle's center is shown in the following picture.

Therefore, the coordinate that represents the point C so that C is the center of the circle is (-1, 3). 34. A square is a parallelogram with four right angles and four congruent sides.

Find the slope of each side of the quadrilateral for each pair of vertices. Slope Slope Slope Slope of QR of RS of ST of TQ S(3,-2)

T(-3,-4) S(2,1)

T(-4,-1) S(1,-1)

T(-5,-3) S(5,2)

T(-4,-1)

Side QR is opposite side ST and side RS is opposite side TQ. If opposite sides have the same slope, then they are parallel. Therefore, the first three quadrilaterals listed above are parallelograms.

If adjacent sides have slopes that are opposite sign reciprocals, then they are perpendicular. Therefore, the first two quadrilaterals listed above have four right angles.

To determine which of the first two quadrilaterals in the table above is a square, calculate the length of two adjacent sides for both pairs of vertices. Length of QR Length of RS S(3,-

2) T(-3,-

4) S(2,1) T(-4,- 1)

Since the first pair of vertices from the above table have adjacent sides that are congruent, then the quadrilateral is a square.

Thus, vertices S(3,-2) and T(-3,-4) make a square when paired with Q(-5,2) and R(1,4).

Since the three sides all have different lengths, the triangle is scalene. Where a, b, and c are the lengths of the sides and c is the longest side, if c2 < a2 + b2, then it is an acute triangle, if c2 = a2 + b2, then it is a right triangle, and if c2 > a2 + b2, then it is an obtuse triangle.

Since the square of the longest side is greater than the sum of the squares of the other two sides, the triangle is obtuse.

Therefore, the triangle is an obtuse scalene triangle.

Since the square of the longest side is equal to the sum of the squares of the other two sides, the triangle is right.

Therefore, the triangle is a right isosceles triangle. 37. A trapezoid is a quadrilateral that contains one pair of parallel sides and one pair of non-parallel sides. The parallel sides are called the bases.

Since JK is one of the bases, it will be parallel to LM. Since the points for J and K have the same x-coordinate, JK is a vertical line segment.

Therefore, point M will have the same x-coordinate as point L, and LM will also be vertical.

Since trapezoid JKLM is isosceles, its two non-parallel sides, KL and MJ, must have equal lengths. Find the length of KL, which is the distance between K(-3,3) and L(1,5).

Find M(x,y) such that the distance to J(-3,0) is .

Thus, the fourth vertex of the isosceles trapezoid is M(1,-2).

38. Parallel lines have the same slope, so to find the correct line, calculate the slope of the line which passes through the given points.

Therefore, the line which passes through the given points is parallel to

40. Lines goes on for infinity in either direction. Line segments are parts of lines that extend from one endpoint to another. Rays extend from one point and go on for infinity in one direction.

A point like Z is a single location on a line.