What Do I See in These Scatter Plots?

Scatter Plots

Quantitative (measurements/counts) Types of Variables Qualitative (groups)

The scatter plot is the basic tool used to investigate relationships between two quantitative variables.

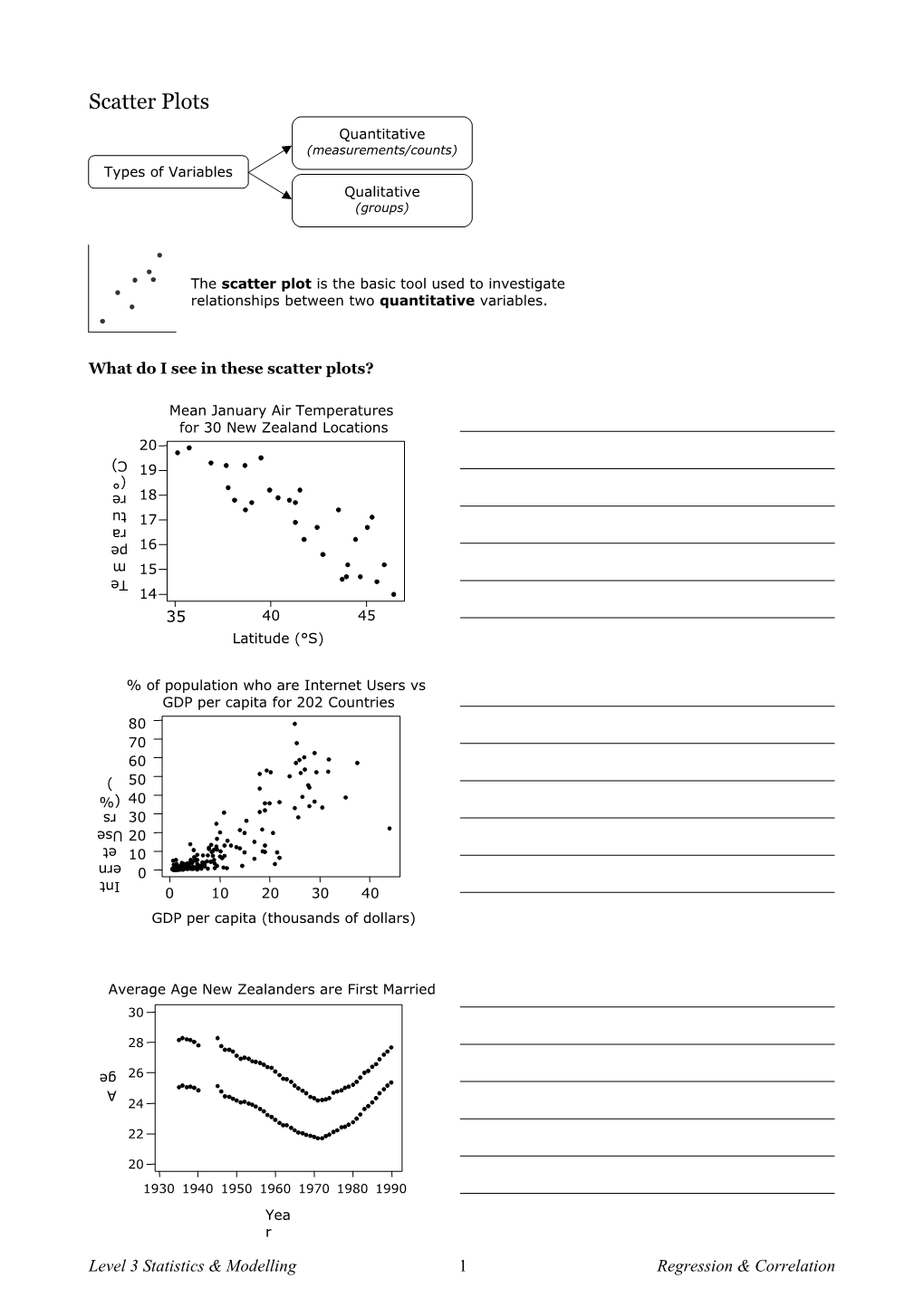
What do I see in these scatter plots?

Mean January Air Temperatures for 30 New Zealand Locations

(° 19

re re 18

ra 17 pe 16

m 15 Te 14 35 40 45 Latitude (°S)

% of population who are Internet Users vs GDP per capita for 202 Countries 80 70

) 50

(% 40 rs rs 30

Use 20

et et 10 ern Int 0 0 10 20 30 40 GDP per capita (thousands of dollars)

Average Age New Zealanders are First Married 30

ge 26 A 24

20 1930 1940 1950 1960 1970 1980 1990 Yea r

Level 3 Statistics & Modelling 1 Regression & Correlation What do I look for in scatter plots?

Trend

Do you see

a linear trend… or a non-linear trend? straight line

Do you see

a positive association… or a negative association? as one variable gets bigger, so as one variable gets bigger, the does the other other gets smaller

Scatter

Do you see

a strong relationship… or a weak relationship? little scatter lots of scatter

Do you see

constant scatter… or non-constant scatter? roughly the same amount of the scatter looks like a “fan” or scatter as you look across the plot “funnel”

Anything unusual

Do you see

any outliers? unusually far from the trend

Do you see

any groupings?

Level 3 Statistics & Modelling 2 Regression & Correlation Rank these relationships from weakest (1) to strongest (4):

How did make your decisions?

Level 3 Statistics & Modelling 3 Regression & Correlation Correlation

. Correlation measures the strength of the linear association between two quantitative variables . Get the correlation coefficient (r) from your calculator or computer . r has a value between -1 and +1:

r = -1 r = -0.7 r = -0.4 r = 0 r = 0.3 r = 0.8 r = 1 Points fall No linear Points fall exactly on a relationship exactly on a straight line (uncorrelated) straight line

. The correlation coefficient has no units

What can go wrong?

. Use correlation only if you have two quantitative variables There is an association between gender and weight but there isn’t a correlation between gender and weight!

. Use correlation only if the relationship is linear . Beware of outliers!

Always plot the data before looking at the correlation!

r = 0 r = 0.9

No linear relationship, but No linear relationship, but

there is a relationship! there is a relationship!

Level 3 Statistics & Modelling 4 Regression & Correlation

Tick the plots where it would be OK to use a correlation coefficient to describe the

s) strength of the relationship:

ile

m 

n n Distances of Planets from the Sun d 

o 0.8

4000 n

illi

m 0.6

3000 H

(

nt nt

e e

2000 a 0.4

1000 m 0.2

Di 0 D 0 0 1 2 3 4 5 6 7 8 9 0 0.2 0.4 0. 0.8 1 Position Number 6 Non-dominant Hand

Mean January Air Temperatures Average Weekly Income for for 30 New Zealand Locations Employed New Zealanders in 2001

20 1200

(° 19 1000

re re 18 800

) tu

ra 17 600 e e

pe 16 400 al m

15 M Te 200 14 0 35 40 45 0 200 400 600 800 Latitude (°S) Female ($)

Level 3 Statistics & Modelling 5 Regression & Correlation What do I see in this scatter plot?

Height and Foot Size

for 30 Year 10 Students

) 200

(c 190

ht ht

g 180

ei H 170

160

150 22 23 24 25 26 27 28 29 Foot size (cm)

What will happen to the correlation coefficient if the tallest Year 10 student is removed? Tick your answer:

(Remember the correlation coefficient answers the question: “For a linear relationship, how well do the data fall on a straight line?”)

It will get smaller It won’t change It will get bigger

What do I see in this scatter plot?

)

rs Life Expectancies and Gestation Period

ea for a sample of non-human Mammals (Y

40 y y

ta Elephant

ec 30

E 20 e e

Lif 10

0 100 200 300 400 500 600 Gestation (Days)

What will happen to the correlation coefficient if the elephant is removed? Tick your answer:

It will get smaller It won’t change It will get bigger

Level 3 Statistics & Modelling 6 Regression & Correlation Using the information in the plot, can you Life Expectancy and Availability of suggest what needs to be done in a country to Doctors for a Sample of 40 Countries

increase the life expectancy? Explain.

y 80

p 70

e e Lif 60

50 0 10000 20000 30000 40000 People per Doctor

Life Expectancy and Availability of Televisions for a Sample of 40 Countries

Using the information in this plot, can you

y 80

p 70

e e Lif 60

50 0 100 200 300 400 500 600 People per Television make another suggestion as to what needs to be done in a country to increase life expectancy?

Level 3 Statistics & Modelling 7 Regression & Correlation Can you suggest another variable that is linked to life expectancy and the availability of doctors (and televisions) which explains the association between the life expectancy and the availability of doctors (and televisions)?

Level 3 Statistics & Modelling 8 Regression & Correlation Causation

Two variables may be strongly associated (as measured by the correlation coefficient for linear associations) but may not have a cause and effect relationship existing between them. The explanation maybe that both the variables are related to a third variable not being measured – a “lurking” or “confounding” variable.

These variables are positively correlated:

. Number of fire trucks vs amount of fire damage . Teacher’s salaries vs price of alcohol . Number of storks seen vs population of Oldenburg Germany over a 6 year period . Number of policemen vs number of crimes

Only talk about causation if you have well designed and carefully carried out experiments.

Data Sources http://www.niwa.cri.nz/edu/resources/climate http://www.cia.gov/cia/publications/factbook http://www.stats.govt.nz http://www.censusatschool.org.nz http://www.amstat.org/publications/jse/jse_data_archive.html

Level 3 Statistics & Modelling 9 Regression & Correlation Going Crackers!

 Do crackers with more fat content have greater energy content?

 Can knowing the percentage total fat content of a cracker help us to predict the energy content?

 If I switch to a different brand of cracker with 100mg per 100g less salt content, what change in percentage total fat content can I expect?

The energy content of 100g of cracker for 18 common cracker brands are shown in the dot plot with summary statistics below. Common Cracker Brands

380 430 480 530 Energy (Calories/100g)

Variable Sample Size Mean Std Dev Min Max LQ UQ

Energy 18 449.0 51.8 375.5 535.6 407.3 506.0

Based on the information above, my prediction for the energy content of a cracker is ______Calories per 100g.

Another quantitative variable which could be useful in predicting (the explanatory variable) the energy content (the response variable) of 100g of cracker is ______.

The Consumer magazine gives some nutritional information from an analysis of these 18 brands of cracker. Some of this information is shown in the table below:

Energy Number of Total Fat Salt (Calories/100g) crackers/100g (%) (mg/100g) 375 16 2.0 600 385 10 2.5 400 408 17 3.5 200 405 56 4.0 500 411 13 4.5 200 405 61 5.0 600 413 5 7.0 700 419 9 7.0 500 426 33 8.0 700 429 7 9.5 900 451 11 14.5 400 484 24 20.5 1300 487 23 22.5 900 505 21 24.0 800 512 16 25.0 700 520 61 27.5 1000 510 31 28.5 1200 536 16 30.5 800

Level 3 Statistics & Modelling 10 Regression & Correlation Common Cracker Brands What do I see in these scatter plots? 550

) 500 g 0 0 y 1 g / r s e e i n

r 450 E o l

(

400 (a) 0 10 20 30 Total Fat (%)

response variable: y-axis explanatory variable: x-axis

Common Cracker Brands 550

) 500 g 0 0 1

r y e g p r

450 e s n e i E r

( 400

200 700 1200 Salt (mg per 100g)

Common Cracker Brands 550

500 ) g 0 0 y 1 g / r s e

e 450 i n r E o l

( 400

0 10 20 30 40 50 60 Number of Crackers/100g

From these plots, the best explanatory variable to use to predict energy content is

______because

______

Level 3 Statistics & Modelling 11 Regression & Correlation Draw a straight line to fit these data (commonly called the fitted line).

550

500 ) g 0 0 y 1 g / r s e e 450 i n r E o

(

400

0 10 20 30 Total Fat (%)

Roughly, my line predicts the energy content for a cracker with a 10% total fat content is about

Calories (per 100g of cracker).

550 Which Line?

500 ) g 0 0 y 1 g / r s e

e 450 i n r E o

(

400

0 10 20 30 Total Fat (%)

Level 3 Statistics & Modelling 12 Regression & Correlation Regression

data point (8, 25) Regression relationship = trend + scatter 25 Observed value = predicted value + prediction error prediction error 21 y = 5 + 2x

Complete the table below 8

Data Point (8, 25) (6, 7) (-2, -3) (x, y)

Observed y-value 25 y

Fitted line yˆ  5  2x yˆ  5  2x yˆ  5  2x yˆ  b0  b1x

Predicted value / fitted value 21 yˆ

Prediction error / residual 4 y - yˆ

The Least Squares Regression Line Which line?

Choose the line with smallest sum of squared prediction errors.

Minimise the sum of squared prediction errors

2 Minimise  prediction errors

 There is one and only one least squares regression line for every linear regression  prediction errors  0 for the least squares line but it is also true for many other lines  (x, y) is on the least squares line

 Calculator or computer gives the equation of the least squares line

Level 3 Statistics & Modelling 13 Regression & Correlation Problem: Predict the energy content of a 100g of cracker which has a total fat content of 25%. Name the variables, the units of We have two quantitative variables, energy (Calories per 100g) measure, and who/what is measured and fat content (%) measured on 18 common cracker brands. (units of interest). Specify the We are investigating the relationship between these two question/problem of interest. variables for the purpose of estimating energy content using the total fat content of a cracker. The scatter plot is the basic tool for Common Cracker Brands investigating the relationship between 2 550 530 quantitative variables. Check for a 510 ) g linear trend – never do a linear 0

0 490 1

r e regression without first looking at the p 470

s e i

r 450 o scatter plot l a C

( 430

y g r

e 410 n E 390

370

350 0 5 10 15 20 25 30 Total Fat (%)

If the assumptions (straightness of line) The data suggests a linear trend. The association is positive appear to be satisfied then fit a linear and very strong. The data suggests constant scatter about regression. the trend line. It is sensible to do a linear regression.

Common Cracker Brands Use a calculator or computer to get the 550 530 equation of the least squares line and 510 ) g 0

0 490 other relevant regression output. 1 y = 4.9844x + 380.82

r e p

470 s e i r

o 450 l a C (

430 y g r

e 410 n E 390

370

350 0 5 10 15 20 25 30 Total Fat (%)

Interpretation: Describe what the The least squares line is yˆ  380.8  4.98x or Predicted equation says in words and numbers. Calories = 381 + 5  Total Fat %. The slope of the fitted line is The slope (y / x) describes how ‘Y’ 5.0 and the y-intercept is 381. changes as ‘X’ changes (the behaviour The regression equation says in crackers, on average, an of Y in terms of X ). increase of about 5 Calories is associated with each 1% Describe what the R2 value says about increase in total fat content. Under this regression, 100g of this regression (see later). a fat free cracker is estimated to contain about 381 Calories. The strong relationship (r = 0.99) means that predictions will be reliable. Use the equation to answer the original Under this regression an estimate of the energy content for question. 100g of a cracker with a 25% total fat content is about 381 + 4.98  25 = 505.5 calories.

Level 3 Statistics & Modelling 14 Regression & Correlation Problem: How does the total fat content of a 100g of cracker change with a 100mg decrease in salt content?

Name the variables, the units of We have two quantitative variables, total fat content (%) and measure, and who/what is measured salt content (mg per 100g) measured on 18 common cracker (units of interest). Specify the brands. We are investigating the relationship between these question/problem of interest. two variables for the purpose of describing how the total fat content changes as the salt content changes. The scatter plot is the basic tool for investigating the relationship between Common Cracker Brands 2 quantitative variables. Check for a linear trend – never do a linear 35 30

regression without first looking at the ) 25 % (

scatter plot t

a 20 F

l 15 a t

o 10 T 5 0 0 500 1000 Salt (mg per 100g)

If the assumptions (straightness of line) appear to be satisfied then fit a linear regression.

Use a calculator or computer to get the equation of the least squares line Common Cracker Brands and other relevant regression output. 35 30 y = 0.0237x - 2.6556 ) 25 % (

a 20 F

l 15 a t

o 10 T 5 0 0 500 1000 Salt (mg per 100g)

Level 3 Statistics & Modelling 15 Regression & Correlation Interpretation: Describe what the Sample correlation coefficient r = 0.69. equation says in words and numbers. The slope (y / x) describes how ‘Y’ changes as ‘X’ changes (the behaviour of Y in terms of X ).

Describe what the R2 value says about this regression (see later).

Use the equation to answer the Under this regression, in a 100g of cracker, a decrease of about original question. 2.4% of total fat content is associated, on average, with each 100mg decrease in salt content.

Another data source

Calorie, fat, carbohydrate, protein content for various foods including fast foods by chain: http://www.healthyweightforum.org/eng/calorie-counter/

Level 3 Statistics & Modelling 16 Regression & Correlation R-squared (R2) On a scatter plot Excel has options for displaying the equation of the fitted line and the value of R2. Four scatter plots with fitted lines are shown below. The equation of the fitted line and the value of R2 are given for each plot.

Common Cracker Brands Common Cracker Brands y = 0.1112x + 372.37 y = 4.9844x + 380.82 550 2 550 2 ) R = 0.982 R = 0.4257 ) g g 0 0 0 0 1 1 / 500 / 500 s s e e i i r r o o l 450 l 450 a a c c ( (

y y g 400 g 400 r r e e n n E 350 E 350 100 300 500 700 900 1100 1300 0 10 20 30 40 Salt (mg/100g) Total Fat (%)

Common Cracker Brands Common Cracker Brands y = 0.3717x + 440.06 y = 0.0237x - 2.6556 550 R2 = 0.0166 2 ) 35 R = 0.4892 g

0 30 0 1 )

/ 500

s 25 % e ( i t r

a 20 o l

450 F

a l

c 15 a ( t

y o 10

g 400 T r

e 5 n E 350 0 0 20 40 60 0 500 1000 1500 Number of crackers per 100g Salt (mg/100g)

Comment on any relationship between the scatter plot and the value of R2. What do you think R2 is measuring?

______

Level 3 Statistics & Modelling 17 Regression & Correlation Look at the scatter plot below. What do you notice?

x Observed value Fitted value y y 55 5.2 23.8 50 5.7 25.8 45 6.5 29.0 40 y 6.9 30.6 35 30 7.8 34.2 25 8.1 35.4 20 4 5 6 7 8 9 10 11 12 8.4 36.6 x 9.1 39.4

10.3 44.2

12.0 51.0

______

R2 (guess) = ______R2 (actual) = ______

Recall: Regression relationship = Trend + scatter

None

There is variability in the x-values, so we expect variability in the fitted values. The variability in the fitted values is exactly the same as the variability in the observed values. The fitted line explains ______of the variability in the observed values.

Level 3 Statistics & Modelling 18 Regression & Correlation Look at the scatter plot below. What do you notice?

x Observed value Fitted value y y

5.2 3.4 9 8 5.7 7.4 7 6.5 4.3 6 5 6.9 7.9 y 4 7.8 4.8 3 2 8.1 5.8 1 0 8.4 2.2 4 6 8 10 12 14 9.1 1.4 x

10.3 6.8

12.0 6.0

______

R2 (guess) = ______R2 (actual) = ______0

Recall: Regression relationship = Trend + scatter

No variability

There is variability in the x-values, so we expect variability in the fitted values. However there was no variability in the fitted values.

The variability in the residuals is exactly the same as the variability in the observed values. The fitted line explains ______of the variability in the observed values.

Level 3 Statistics & Modelling 19 Regression & Correlation Consider the scatter plot and table below. The equation of the fitted line is displayed on the plot.

x Observed value Fitted value Residual y y 5.2 20.1 16.3 3.8 5.7 15.4 18.0 -2.6 6.5 18.7 20.8 -2.1 6.9 22.0 22.2 -0.2 7.8 24.0 25.4 -1.4 8.1 24.4 26.4 -2.0 8.4 26.9 27.5 -0.6 9.1 34.8 29.9 4.9 10.3 37.2 34.1 3.1 12.0 37.2 40.0 -2.8

45 y = 3.4883x - 1.8364 40

35 30 y 25 20

15 10 4 6 8 10 12 14 x

Recall: Regression relationship = Trend + scatter

3. This shows the variability in the observed values that is not explained by the linear regression. 1. This shows the variability in the observed values.

2. From the variability in the x-values this shows the variability in the observed values explained by the linear regression.

R2 = 0.866

Level 3 Statistics & Modelling 20 Regression & Correlation R-squared

 R2 gives the fraction of the variability of the y-values accounted for by the linear regression (considering the variability in the x-values).  R2 is often expressed as a percentage.  If the assumptions (straightness of line) appear to be satisfied then R2 gives an overall measure of how successful the regression is in linearly relating y to x.  R2 lies from 0 to 1 (0% to 100%).  The smaller the scatter about the regression line the larger the value of R2.  Therefore the larger the value of R2 the greater the faith we have in any estimates using the equation of the regression line.  R2 is the square of the sample correlation coefficient, r.  For the above example, the linear regression accounts for 86.6% of the variability in the y- values from the variability in the x-values. Exercise: List the plots from greatest R2 to least R2. A Cement hardness B Optical absorbance versus dissolved carbon

50 0.1

0.09 40 0.08 e

) c 0.07 s n t i a

n 30 b 0.06 r u ( o

s s 0.05 b s a e

l n 20 a 0.04 d c r i t a p H 0.03 O 10 0.02 0.01

0 0 150 200 250 300 350 400 0 0.5 1 1.5 2 2.5 3 Cem ent (gram s) Dissolved organic carbon (m g/L)

C D Reaction times, Olympic 100m Road conditions in Canada

12 80

11.5 x e

d 70 n i

) n s o d 11 i t n i o d c n

e 60 o s c (

t e 10.5 n m e i T m e

v 50 a

10 P

9.5 40 0.1 0.12 0.14 0.16 0.18 0.2 0.22 0.24 10 11 12 13 14 15 16 17 18 19 Reaction tim e (seconds) Age (years)

Greatest to least R2: ______Source: Chance Encounters: A First Course in Data Analysis and Inference by Christopher J. Wild and George A. F. Seber

Level 3 Statistics & Modelling 21 Regression & Correlation For each scatter plot, use the value of R2 to write a sentence about the variability of the y-values accounted for by the linear regression.

Common Cracker Brands ______y = 0.1112x + 372.37 550 2 ) R = 0.4257

g ______0 0 1

/ 500 s e i

r ______o

l 450 a c (

g 400 ______r e n

E 350 100 300 500 700 900 1100 1300 Salt (mg/100g) Common Cracker Brands y = 4.9844x + 380.82 ______550 R2 = 0.982 ) g 0

0 ______1

/ 500 s e i r o

l 450

a ______c (

g 400 r e

n ______E 350 0 10 20 30 40 Total Fat (%) Common Cracker Brands y = 0.3717x + 440.06 ______550 R2 = 0.0166 ) g 0

0 ______1

/ 500 s e i r o l 450 ______a c (

g 400 r

e ______n

E 350 0 20 40 60 Number of crackers per 100g Common Cracker Brands y = 0.0237x - 2.6556 ______35 R2 = 0.4892 30 ) 25 ______% (

a 20 F

l 15 a

t ______o 10 T 5 0 ______0 500 1000 1500 Salt (mg/100g)

Level 3 Statistics & Modelling 22 Regression & Correlation Outliers (in a regression context)

An outlier, in a regression context, is a point that is unusually far from the trend.

The following table shows the winning distances in the men’s long jump in the Olympic Games for years after the Second World War.

Year Winner Distance Year Winner Distance 1948 Willie Steele (USA) 7.82m 1980 Lutz Dombrowski (GDR) 8.54m 1952 Jerome Biffle (USA) 7.57m 1984 Carl Lewis (USA) 8.54m 1956 Gregory Bell (USA) 7.83m 1988 Carl Lewis (USA) 8.72m 1960 Ralph Boston (USA) 8.12m 1992 Carl Lewis (USA) 8.67m 1964 Lynn Davies (GBR) 8.07m 1996 Carl Lewis (USA) 8.50m 1968 Bob Beamon (USA) 8.90m 2000 Ivan Pedroso (Cuba) 8.55m 1972 Randy Williams (USA) 8.24m 2004 Dwight Phillips (USA) 8.59m 1976 Arnie Robinson (USA) 8.35m Source: http://www.sporting-heroes/stats_athletics/olympics_trackandfield/trackfield.asp

Men's Long Jump Winning Distances, Olympic Games, 1948-2004

9 ) s e

r 8.5 t e m (

e 8 c n a t

s 7.5 i D 7 0 10 20 30 40 50 60 Years since 1944

Comment on the scatter plot.

______

Level 3 Statistics & Modelling 23 Regression & Correlation Excel output for a linear regression on all 15 observations

Men's Long Jump Winning Distances, Olympic Games, 1948-2004 y = 0.0164x + 7.8097 9 R2 = 0.5914

) s e

r 8.5 t e m (

e 8 c n a t

s 7.5 i D 7 0 10 20 30 40 50 60 Years since 1944

We estimate that for every 4-year increase in years (from one Olympic Games to the next) the

winning distance increases by ______, on average.

Using this linear regression we predict that the winning distance in 2004 will be ______.

Excel output for a linear regression on 14 observations (with the 1968 observation removed)

Men's Long Jump Winning Distances, Olympic Games, 1948-2004 (excl.1968)

y = 0.0177x + 7.7158 9 R2 = 0.8213

) s e

r 8.5 t e m (

e 8 c n a t s

i 7.5 D

7 0 10 20 30 40 50 60 Years since 1944

We estimate that for every 4-year increase in years (from one Olympic Games to the next) the

winning distance increases by ______, on average.

Using this linear regression we predict that the winning distance in 2004 will be ______.

Level 3 Statistics & Modelling 24 Regression & Correlation What effect did the 1968 observation have on the: fitted line? ______

______

______predicted winning distance in 2004? ______value of R2? ______

An outlier, in a regression context, is a point that is unusually far from the trend.

 An outlier should be checked out to see if it is a mistake or an actual unusual observation.

 If it is a mistake then it should either be corrected or removed.

 If it is an actual unusual observation then try to understand why it is so different from the other observations.

 If it is an actual unusual observation (or we don’t know if it is a mistake or an actual observation) then carry out two linear regressions; one with the outlier included and one with the outlier excluded. Investigate the amount of influence the outlier has on the fitted line and discuss the differences.

Level 3 Statistics & Modelling 25 Regression & Correlation Outliers in X (or x-outliers) We often talk about a person’s “blood pressure” as though it is an inherent characteristic of that person. In fact, a person’s blood pressure is different each time you measure it. One thing it reacts to is stress. The following table gives two systolic blood pressure readings for each of 20 people sampled from those participating in a large study. The first was taken five minutes after they came in for the interview, and the second some time later. Note: The systolic phase of the heartbeat is when the heart contracts and drives the blood out. Source: Chance Encounters: A First Course in Data Analysis and Inference by Christopher J. Wild and George A. F. Seber (Exercise for Section 3.1.2., Question 3, p113).

Observatio 1 2 3 4 5 6 7 8 9 10 n 1st reading 116 122 136 132 128 124 110 110 128 126 2nd reading 114 120 134 126 128 118 112 102 126 124 Observatio 11 12 13 14 15 16 17 18 19 20 n 1st reading 130 122 134 132 136 142 134 140 134 160 2nd reading 128 124 122 130 126 130 128 136 134 160

Blood Pressure

160

150 g n

i 140 d a e r

130 d n o

c 120 e S 110

100 100 110 120 130 140 150 160 First reading

Comment on the scatter plot.

______

Level 3 Statistics & Modelling 26 Regression & Correlation Excel output for a linear regression on all 20 observations

Blood Pressure y = 0.9337x + 4.9068 160 R2 = 0.8673

150 g

n 140 i d a e r

130 d n o

c 120 e S 110

100 100 110 120 130 140 150 160 First reading

We estimate that for every 10-unit increase in the first blood pressure reading the second

reading increases by ______, on average.

For a person with a first reading of 140 units we predict that the second reading will be

______

Excel output for a linear regression on 19 observations (Observation 20 removed)

Blood pressure (Obs 20 removed)

y = 0.8124x + 20.152 160 R2 = 0.7844

150 g n

i 140 d a e r

130 d n o

c 120 e S 110

100 100 110 120 130 140 150 160 First reading

We estimate that for every 10-unit increase in the first blood pressure reading the second

reading increases by ______, on average.

For a person with a first reading of 140 units we predict that the second reading will be

______

Level 3 Statistics & Modelling 27 Regression & Correlation What effect did observation 20 have on the: fitted line?

______predicted second reading (for a first reading of 140)?

______value of R2?

______

An x-outlier is a point with an extreme x-value.

 An x-outlier can alter the position of the fitted line substantially, i.e. it can influence the position of the fitted line.

 The fitted line may say more about the x-outlier than about the overall relationship between the two variables.

 An x-outlier is sometimes called a high-leverage point.

 If a data set has an x-outlier then carry out two linear regressions; one with the x-outlier included and one with the x-outlier excluded. Investigate the amount of influence the x-outlier has on the fitted line and discuss the differences.

Level 3 Statistics & Modelling 28 Regression & Correlation Groupings In the 1930s Dr. Edgar Anderson collected data on 150 iris specimens. This data set was published in 1936 by R. A. Fisher, the well-known British statistician. This data set is widely available. I sourced it from: http://lib.stat.cmu.edu/DASL/Stories/Fisher’sIrises.html

Fisher's Iris Data

25 )

m 20 m (

h t

d 15 i w

l a

t 10 e P 5

0 0 10 20 30 40 50 60 70 80 Petal length (mm)

Comment on the scatter plot.

______

Fisher's Iris Data

y = 0.407x - 3.4532 30 R2 = 0.9137 25 )

m 20 m (

h t

d 15 i w

a 10 t e P 5

0 0 10 20 30 40 50 60 70 80 Petal length (mm)

Level 3 Statistics & Modelling 29 Regression & Correlation The data were actually on fifty iris specimens from each of three species; Iris setosa, Iris versicolor and Iris verginica. The scatter plot below identifies the different species by using different plotting symbols (+ for setosa, • for versicolor, × for verginica).

Let’s see what happens when we look at the groups separately.

Fisher's Iris Data (Iris setosa) Fisher's Iris Data (Iris versicolor) y = 0.2012x - 0.4822 y = 0.2273x + 3.437 7 20 R2 = 0.11 R2 = 0.3797 6 18 ) )

m 5 m 16 m m ( (

4 h h t t d d

i 14 i

w 3 w

l l a a t

t 12

e 2 e P P 1 10

0 8 8 10 12 14 16 18 20 25 30 35 40 45 50 55 60 Petal length (mm) Petal length (mm)

Fisher's Iris Data (Iris verginica) y = 0.1839x + 9.8509 30 R2 = 0.1222

) 25 m m (

h t

d 20 i w

l a t e

P 15

10 40 45 50 55 60 65 70 75 Petal length (mm)

Comment.

______

Level 3 Statistics & Modelling 30 Regression & Correlation Watch for different groupings in your data.

 If there are groupings in your data that behave differently then consider fitting a different linear regression line for each grouping.

More about R2.

 A large value of R2 does not mean the linear regression is appropriate.

 An x-outlier or data that has groupings can make the value of R2 seem large when the linear regression is just not appropriate.

 On the other hand, a low value of R2 may be caused by the presence of a single outlier and all other points have a reasonably strong linear relationship.

Level 3 Statistics & Modelling 31 Regression & Correlation Prediction The data in the scatter plot below were collected from a set of heart attack patients. The response variable is the creatine kinase concentration in the blood (units per litre) and the explanatory variable is the time (in hours) since the heart attack. Source: Chance Encounters: A First Course in Data Analysis and Inference by Christopher J. Wild and George A. F. Seber, p514.

Creatine kinase concentration

1200 ) e

r 1000 t i l / s t i 800 n u (

n 600 o i t a r t 400 n e c n

o 200 C

0 0 2 4 6 8 10 12 14 16 18 Time (hours)

Comment on the scatter plot.

______

Suppose that a patient had a heart attack 17 hours ago. Predict the creatine kinase concentration in the blood for this patient.

______

In fact their creatine kinase concentration was 990 units/litre. Comment.

______

Level 3 Statistics & Modelling 32 Regression & Correlation The complete data set is displayed in the scatter plot below.

Creatine kinase concentration

1200 ) e

r 1000 t i l / s t

i 800 n u (

n 600 o i t a r t 400 n e c n

o 200 C

0 0 10 20 30 40 50 60 Time (hours)

Beware of extrapolating beyond the data.

 A fitted line will often do a good job of summarising a relationship for the range of the observed x-values.

 Predicting y-values for x-values that lie beyond the observed x-values is dangerous. The linear relationship may not be valid for those x-values.

More about x-outliers.

 The removal of an x-outlier will mean that the range of observed x-values is reduced. This should be discussed in the comparison between the two linear regressions (x-outlier included and x-outlier excluded).

Level 3 Statistics & Modelling 33 Regression & Correlation Non-Linearity The data in the scatter plot below shows the progression of the fastest times for the men’s marathon since the Second World War. We may want to use this data to predict the fastest time at 1 January 2010 (i.e. 64 years after 1 January 1946). Source: http://www.athletix.org/

Men's Marathon Fastest Times

150

145 ) s

e 140 t u n i 135 m (

e m

i 130 T

125

120 0 10 20 30 40 50 60 Years since 1 Jan 1946

Concerns:

______

Possible solutions:

______

Level 3 Statistics & Modelling 34 Regression & Correlation Men's Marathon Fastest Times Men's Marathon Fastest Times

y = 0.0078x2 - 0.769x + 144.68 y = 139.99e-0.0022x 150 150 2 R2 = 0.9592 R = 0.8521

145 145 ) ) s s

e 140 140 e t t u u n n i 135 i

m 135 m ( (

e e m m

i 130

i 130 T T

125 125

120 120 0 10 20 30 40 50 60 0 10 20 30 40 50 60 Years since 1 Jan 1946 Years since 1 Jan 1946

Men's Marathon Fastest Times

y = 151.08x-0.0452 155 R2 = 0.9401 150

) 145 s e t

u 140 n i m ( 135 e m i

T 130

125

120 0 10 20 30 40 50 60 Years since 1 Jan 1946

Men's Marathon Fastest Times, Men's Marathon Fastest Times, 1946-69 1969-2003

y = -0.6537x + 144.69 y = -0.1089x + 131.66 148 2 130 R2 = 0.9024 146 R = 0.9366 144 129 ) )

s 142 s e e t 140 t 128 u u n n i

138 i

m 127 m (

136 (

e 134 e m

m 126 i i

T 132 T 130 125 128 126 124 0 5 10 15 20 25 20 30 40 50 60 Years since 1 Jan 1946 Years since 1 Jan 1946 Comments:

______

Level 3 Statistics & Modelling 35 Regression & Correlation The data in the scatter plot below comes from a random sample of 60 models of new cars taken from all models on the market in New Zealand in May 2000. We want to use the engine size to predict the weight of a car.

Models of New Zealand Cars

2000

) 1500 g k (

t h g i e

W 1000

500 1000 2000 3000 4000 5000 6000 Engine size (cc)

Concerns:

______

Possible solutions:

______

Level 3 Statistics & Modelling 36 Regression & Correlation Investigations

Cars Use the car data (Cars.xls) to investigate the following questions:  Can the size of a car’s engine be used to determine its weight?  Do any of the variables help to explain the price of a car?  Do any other pairs of variables have interesting relationships?

Life Expectancy Use the life expectancy data (CIA Life Expectancy.xls) to investigate the following questions:  What is the life expectancy of a male who lives in a country in which the female life expectancy is 78 years?  Can you determine the life expectancy of the people (total or male or female) in a country by using the fertility rate for women in that country?

Body Fat % It is difficult to accurately determine a person's body fat percentage. One of the best methods requires immersing a person in water which is not always practical. Researchers immersed 20 male subjects and were able to estimate their body fat percentage. They also weighed the males and measured their waists. The body fat data (Body Fat.xls) gives the results of this study. Using these data create the best model to predict body fat from either using weight or waist measurements of a male from the population underlying this random sample.

Note: Be sure to follow the steps shown in class when writing up the report. The regression interpretation step is very important. Data for each investigation:

http://www.stat.auckland.ac.nz/~u47510x/teachers/2003/regression/ComputerLab.zip

Level 3 Statistics & Modelling 37 Regression & Correlation