The Journal of Experimental Psychology Applied (June 2000) Published a Study in Which The

Simple Linear Regression Example

The Journal of Experimental Psychology – Applied (June 2000) published a study in which the “name game” was used to help groups of students learn the names of other students in the group. The “name game” requires the first students in the group to state his/her full name, the second student to say his/her name and the name of the first student, the third student to say his/her name and the names of the first two students, etc. After making their introductions, the students listened to a seminar speaker for 30 minutes. At the end of the seminar, all students were asked to remember the full name of each of the other students in the group and the researchers measured the proportion of names recalled for each. One goal of the study was to investigate the linear trend between Y=recall proportion and X=position (order) of the students during the game.

Assume a simple linear regression model holds for the relationship between Y and X.

(a) What sign would you expect the slope to have?

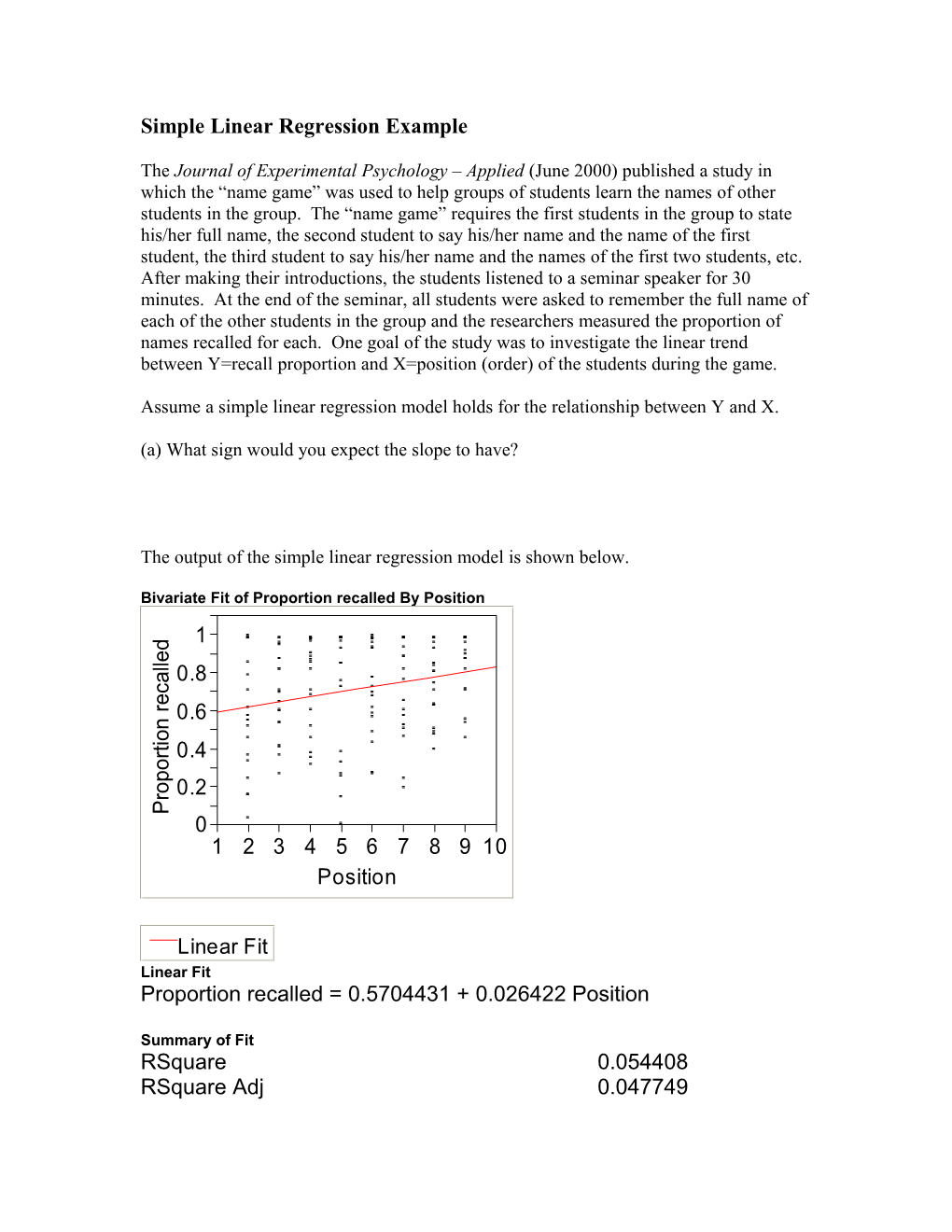
The output of the simple linear regression model is shown below.

Bivariate Fit of Proportion recalled By Position 1 d e l l

a 0.8 c e r

0.6 n o i t

r 0.4 o p

o 0.2 r P 0 1 2 3 4 5 6 7 8 9 10 Position

Linear Fit Linear Fit Proportion recalled = 0.5704431 + 0.026422 Position

Summary of Fit RSquare 0.054408 RSquare Adj 0.047749 Root Mean Square Error 0.254156 Mean of Response 0.715764 Observations (or Sum Wgts) 144

Analysis of Variance Source DF Sum of Squares Mean Square F Ratio Model 1 0.5277786 0.527779 8.1705 Error 142 9.1725374 0.064595 Prob > F C. Total 143 9.7003160 0.0049

Parameter Estimates Term Estimate Std Error t Ratio Prob>|t| Intercept 0.5704431 0.055075 10.36 <.0001 Position 0.026422 0.009244 2.86 0.0049

(b) According to the model, what is the mean proportion recalled for students in the fifth position?

(c) According to the model, what is the mean proportion recalled for students in the 20th position?

(d) Which would you consider to be more accurate, the estimate of the mean proportion recalled for students in the fifth position from (b) or the estimate of the mean proportion recalled for students in the 20th position from (c)? Why?

(e) Use the simple linear regression model to find an interval that should contain the proportion recalled for a randomly chosen student in the fifth position about 95% of the time.