PT Chapter 4 TEST – AP Calculus Name:
Part A No Calculator
b b 1. If f (x) dx a 2b , then ( f (x) 5) dx a a
(A) a 2b 5 (B) 5b 5a (C) 7b 4a (D) 7b 5a (E) 7b 6a
Questions 2 – 4 refer to the following situation.
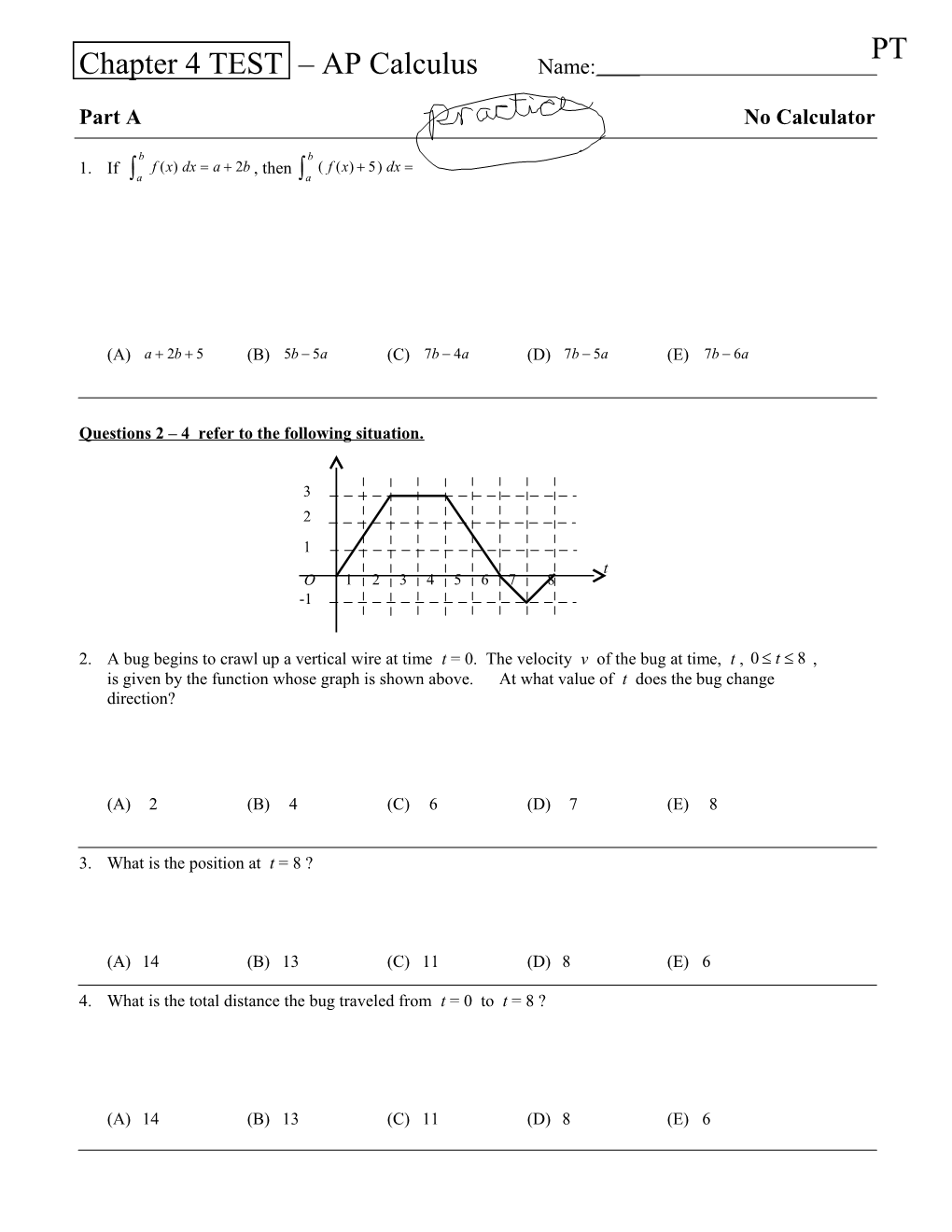
3 2 1 t O 1 2 3 4 5 6 7 8 -1
2. A bug begins to crawl up a vertical wire at time t = 0. The velocity v of the bug at time, t , 0 t 8 , is given by the function whose graph is shown above. At what value of t does the bug change direction?
(A) 2 (B) 4 (C) 6 (D) 7 (E) 8
3. What is the position at t = 8 ?
(A) 14 (B) 13 (C) 11 (D) 8 (E) 6
4. What is the total distance the bug traveled from t = 0 to t = 8 ?
(A) 14 (B) 13 (C) 11 (D) 8 (E) 6 PT Part A No Calculator
5. The average value of cos x on the interval [ -3 , 5 ] is
sin 5 sin 3 sin 5 sin 3 sin 3 sin 5 (A) (B) (C) 8 2 2 sin 3 sin 5 sin 3 sin 5 (D) (E) 2 8
1 1 2 3 50 6. The expression . . . is a Riemann sum approximation for 50 50 50 50 50
1 x 1 1 1 x 1 1 1 50 (A) dx (B) x dx (C) dx (D) x dx (E) x dx 0 50 0 50 0 50 50 0 50 0
v (t) ( 4 , 16 ) ( 16 , 16 )
t | | | | | | 4 8 12 16 20 24
7. A car is traveling on a straight road. For 0 t 24 seconds, the car’s velocity v(t) , in meters per second, is modeled by the piecewise-linear function defined by the graph above. If the car takes 24 seconds to reach the 400 meter mark, then what was its initial position? (A) 104 meters (B) 112 meters (C) 120 meters (D) 128 meters (E) 136 meters PT Part A No Calculator
y 6 y f '(x)
( 4 , 3 )
x O 4
8. The graph of f ', the derivative of f, is the line shown in the figure above. If f (0) = 5, then f (3) =
(A) 13 (B) 17 (C) 20 (D) 21 (E) 23
y ( 6 , 5 ) ( 8 , 5 )
O 2 10 x
( -4 , -2 ) -2
10 9. Use the graph of f (x) in the figure shown above to evaluate f (x) dx . 4 (A) 12 (B) 13 (C) 15 (D) 16.5 (E) 20.5
y Gallons per 4 minute
2
O 5 10 15 20 minutes
10. The rate at which a faucet pours water into a tank is shown in the graph above. If the tank is completely empty at t = 0 minutes, then to the nearest whole number, the amount of water in the tank at 20 minutes is about (A) 10 gallons (B) 20 gallons (C) 30 gallons (D) 40 gallons (E) 50 gallons
PT Part A No Calculator
x 0 2 3 6 8 f ( x ) 2 4 5 9 12
8 11. Use the table above to find a trapezoidal approximation of f (x) dx . 0
(A) 52.5 (B) 55 (C) 56.5 (D) 58 (E) 60
2 3 sin 0.5x dx 12. 3
3 1 3 1 (A) (B) 3 1 (C) 6 6 2 2 3 1 (D) 2 3 1 (E) 6 6
2 3 13. x 2x 5 dx 1 33 1 57 63 87 (A) (B) (C) (D) (E) 4 4 4 4 4
PT Part B Graphing Calculator Required
Stop! You may use your graphing calculator for the remainder of the test.
Questions 14 – 16 refer to the following graph. y = f (x)
B x -3 A O C 3
14. The regions A, B, and C in the figure above are bounded by the graph of the function f and the x-axis. If the 3 area of each region is 4, then the value of f (x) dx 3
(A) -4 (B) -2 (C) 0 (D) 4 (E) 8
1 15. The value of f (x 2) dx 5
(A) -4 (B) -2 (C) 0 (D) 4 (E) 8
3 16. The value of ( f (x) 2) dx 3
(A) -4 (B) -2 (C) 0 (D) 4 (E) 8 PT Part B Graphing Calculator Required
17. What is the average velocity, in ft/sec, of a particle moving a straight path from time t = 0 to time t = 2 if the velocity function is v(t) t 2et t et ?
(A) 7.086 ft/sec (B) 9.447 ft/sec (C) 10.584 ft/sec (D) 11.924 ft/sec (E) 13.342 ft/sec
t minutes 0 8 10 15 f (t) miles per hour 8 5 6 4
18. The function f (t) is continuous on the closed interval 0 t 15 and represents the speed of a jogger recorded only at the start, 8, 10, and 15 minutes. What is the trapezoidal approximation of his total distance traveled?
(A) 1 mile (B) 1.25 miles (C) 1.333 miles (D) 1.467 miles (E) 1.5 miles
19. Let f be the function defined by
2x 3 0 x 3 f (x) 6 x 3 x 5. Which of the following is false?
(a) f is continuous at x = 3. (b) f is not differentiable at x = 3. (c) The average value of f (x) on the closed interval 0 x 5 is 4.423. lim f (x) f (3) (d) x 3 . 1 5 (e) f (x) dx 2.254 . 5 0 PT Part B Graphing Calculator Required
y
2
1
x O 1 2 3 4
2 20. The graph of f is shown above such that f F '(x) and f is symmetrical about x = 2 . If f (t) dt 1.2 , 0 then F(4) F(0)
(A) 0 (B) 0.6 (C) 1.2 (D) 2.4 (E) 3.6
1 4 4 4 21. If f (t) dt 1 and 3g(t) dt 1 , then what is f (t) g(t) dt ? 2 2 2 2 7 8 10 1 (A) (B) (C) 3 (D) (E) 3 3 3 3
22. On the closed interval [ 2 , 4 ], the average value of a function f is 1. Which of the following could be the graph of a function f ?
(A)4 — (B)4 — (C)4 — 3 — 3 — 3 — 2 — 2 — 2 — 1 — 1 — 1 — | | | | | | | | | | | | O 1 2 3 4 O 1 2 3 4 O 1 2 3 4
(D)4 — (E)4 — 3 — 3 — 2 — 2 — 1 — 1 — | | | | | | | | O 1 2 3 4 O 1 2 3 4
PT Part B Graphing Calculator Required
1 1 dx 23. 4 3 x x 2
1 1 3 3 1 2 3x 3 C C 3x 3 C (A) (B) 3 3 (C) 3x3 x x 3x3 1 2 5 3 3x 3 C C (D) (E) 5 3 5x5 x x
Free Response Graphing Calculator Required
4 24. Sketch a graph of y f (x) on the interval 0 x 4 whose trapezoidal sum underapproximates f (x) dx , and 0 4 a right Riemann sum also underapproximates f (x) dx . 0 PT Free Response Practice Graphing Calculator Required
25. The rate at which people enter an amusement park on a given day is modeled by the function E defined by
15600 E(t) . (t 2 24t 160)
The rate at which people leave the same amusement park on the same day is modeled by the function L defined by 9892 L(t) . (t 2 38t 370)
Both E(t) and L(t) are measured in people per hour and time t is measured in hours after midnight. These functions are valid for 9 t 23, the hours during which the park is open. At time t = 9, there are no people in the park.
(a) How many people have entered the park by 5:00 P.M. ( t = 17 ) ? Round your answer to the nearest whole number. (b) The price of admission to the park is $15 until 5:00 P.M. ( t = 17 ). After 5:00 P.M., the price of admission to the park is $11. How many dollars are collected from admissions to the park on the given day? Round your answer to the nearest whole number. (c) At what time t , for 9 t 23, does the model predict that the number of people in the park is a maximum? Also study the first three tests and especially the last worksheet – AP Questions Involving The Fundamental Theorem of Calculus.
ANSWERS: 1) C 6) B 11) A 16) E 21) A 24) 2) C 7) B 12) B 17) C 22) E 3) C 8) E 13) D 18) D 23) A 4) B 9) C 14) A 19) C 5) E 10) D 15) A 20) D 4
17 17 23 25 a) E(t)dt 6004 b) 15 E(t)dt 11 E(t)dt $104,048 9 9 17
c) Total Number of people = Number of people Entering – Number of people Leaving OR p (t) = e (t) – l (t)
Maximize p (t) by taking the derivative and setting p’ (t) = 0 ,
p' (t) = e’ (t) – l’ (t) = 0
Since e’ (t) is really E (t) and l’ (t) is really L (t) , we have
E (t) – L (t) = 0 E (t) = L (t)