Department of Electrical and Computer Engineering s9

DREXEL UNIVERSITY

DEPARTMENT OF ELECTRICAL AND COMPUTER ENGINEERING ECE-C 490 Image Processing Architectures Winter, 2002-03 Homework 3. Solution

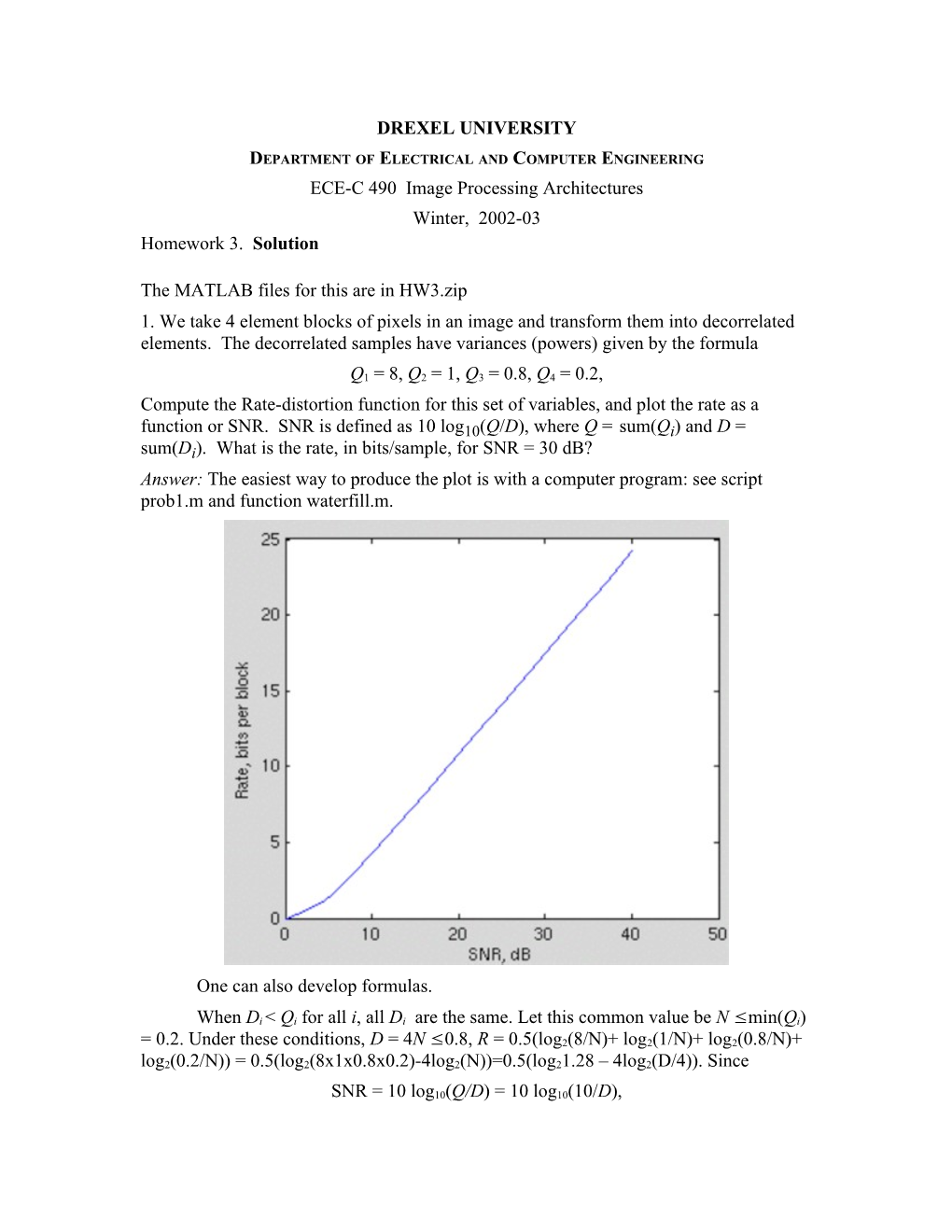
The MATLAB files for this are in HW3.zip 1. We take 4 element blocks of pixels in an image and transform them into decorrelated elements. The decorrelated samples have variances (powers) given by the formula

Q1 = 8, Q2 = 1, Q3 = 0.8, Q4 = 0.2, Compute the Rate-distortion function for this set of variables, and plot the rate as a function or SNR. SNR is defined as 10 log10(Q/D), where Q = sum(Qi) and D = sum(Di). What is the rate, in bits/sample, for SNR = 30 dB? Answer: The easiest way to produce the plot is with a computer program: see script prob1.m and function waterfill.m.

One can also develop formulas.

When Di < Qi for all i, all Di are the same. Let this common value be N ≤ min(Qi) = 0.2. Under these conditions, D = 4N ≤ 0.8, R = 0.5(log2(8/N)+ log2(1/N)+ log2(0.8/N)+ log2(0.2/N)) = 0.5(log2(8x1x0.8x0.2)-4log2(N))=0.5(log21.28 – 4log2(D/4)). Since

SNR = 10 log10(Q/D) = 10 log10(10/D), D = 10/(10^(SNR/10)) = 10^(1 – SNR/10). Substituting into the above formula, we get

R = 0.5(log21.28 – 4log2((10^(1-SNR))/4)) = 0.664 SNR – 2.47 At SNR = 30 db, R = 17.5 bits. 2. Quantize image lena.tiff with  = 15. Dequantize, and compute the rms error. Compare the actual error with that predicted by the formula  = 0.287. Answer: See function prob2.m The formula predicts 4.33, the actual error is 4.26. The formula is pretty good (in this case).

3. Using the method of 2, vary the quantization step, and for each value of step find the entropy and the rms error. Plot the distortion – rate tradeoff, with PSNR on the horizontal axis and bits/pixel on the vertical. Answer: See script prob3.m, which calls function prob2.m (which, in turn, calls hist.m and H.m). The plot is below.

The PSNR is quite well predicted by the formula

20 log10 (255/(step/sqrt(12))) = 59 – 20log10 (step) The entropy for step = 1 is equal to 7.22. (This is the entropy for the unquantized image). Each time the step is doubled, one bit is dropped. The entropy is given (approximately) by

H = 7.22 – log2(step). 4. A program for computing and plotting the histogram as well as computing entropy is in lena_H.m. Run this program. What is the entropy of the lena picture? Write a program to find the histogram of the differences of successive pixels in picture lena.tiff. Use this as an estimate of the probability distribution, and compute the entropy. Note the differences fall in the range -255 ≤ d ≤ 255. Compare this entropy with that computed by lena_H. What is the compression?

The entropy is 7.22. If all probabilities of gray values were the same, the entropy would be 8. We see that there is very little to be gained from entropy coding; See script prob4.m, derived from lena_H.m. It computes the difference, its histogram and the entropy. Answer: See file prob4.m. The entropy is 4.454. and the histogram is as plotted. This indicates that entropy coding of pixel differences would produce almost a two-fold lossless compression. We are given the following 8x8 block of gray values. (These data are available in file block.txt. They were obtained from lena.tiff, 129≤ row, column ≤ 136) 16 16 16 13 11 10 94 98 4 3 2 8 0 2 0 0 16 16 14 13 11 10 96 98 3 1 4 3 2 3 0 0 17 15 13 11 11 10 97 10 4 2 5 9 1 8 0 2 16 15 13 11 11 10 10 10 2 0 0 8 6 5 0 1 15 14 12 12 10 10 93 10 1 2 3 5 4 9 0 0 14 14 12 11 11 10 10 95 4 1 9 9 3 8 2 14 13 11 11 11 10 10 95 2 7 8 8 1 3 2 15 12 11 11 11 11 10 98 3 1 6 5 5 5 3 (a) Subtract 128 and compute the 2-D DCT of this array. (You may do this with a program or a spreadsheet, whichever you prefer. A program for doing this sort of calculation is on the notes page.) Which k, l coefficient has the largest value? Verify that the sum of the squares of the DCT coefficients is equal to the sum of squares of the gray values. Answer: This is in script prob5.m. The array of DCT coefficients (rounded to the nearest integer) is: -51 35 5 -1 1 2 5 -4 160 41 3 5 -1 3 0 1 30 5 -8 -12 -1 2 2 4 11 -22 -6 -18 0 -2 4 0 7 -5 -1 -9 3 -2 -1 3 1 -3 6 0 3 -2 2 2 4 3 3 -4 6 -4 8 4 -7 -1 4 -4 -1 7 5 -7 The largest coefficient is 159.89 in row 2, column 1. The sum of the squares of the DCT coefficients is 33919, same as the sum of the squares of the image values (after subtraction). (b) Quantize the DCT coefficients with  = 32. Assume that the compression for the block is estimated by the ratio of the total number of DCT coefficients to the number of non-zero quantized coefficients. Estimate the compression. Answer: The quantized values are -2 1 0 0 0 0 0 0 5 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 -1 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 There are 7 nonzero coefficients, so that the compression is 64/7 = 9.14. (c) Compute the quantization noise, defined as 7 7 1 * 2 N = е е (dkl- dkl) 64 k=0 l=0 , where

are the (unquantized) DCT coefficients, and *

are the quantized /dequantized DCT coefficients. Answer: The quantization noise is 27.4. Note that our rule of thumb is Step^2/12 = 83.3. Can you suggest why the rule of thumb produces an overestimate? (d) Compute the inverse DCT of the quantized coefficients, and find the average squared difference between these values and the original gray values. Compare this with the value of N found in (c). Answer: The average squaredd difference is 27.4, the same as the answer in (c). kl