For Simplicity, Let's Start with Binary Composites

For simplicity, let's start with binary composites: Component A, with Young's modulus Ea and volume fraction fa; Component B, with Young's modulus Eb and volume fraction fb.

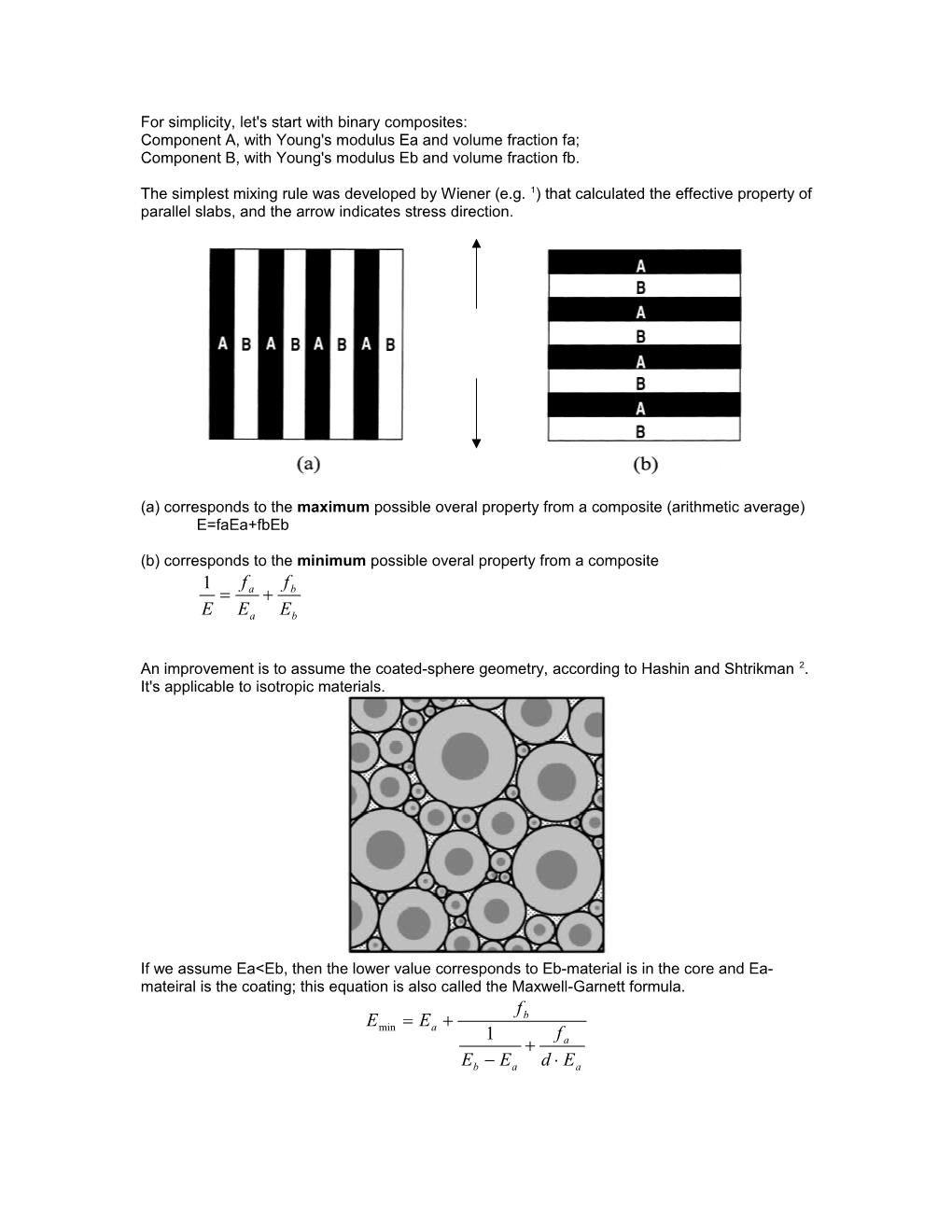
The simplest mixing rule was developed by Wiener (e.g. 1) that calculated the effective property of parallel slabs, and the arrow indicates stress direction.

(a) corresponds to the maximum possible overal property from a composite (arithmetic average) E=faEa+fbEb

(b) corresponds to the minimum possible overal property from a composite 1 f f  a  b E Ea Eb

An improvement is to assume the coated-sphere geometry, according to Hashin and Shtrikman 2. It's applicable to isotropic materials.

If we assume Ea

f E  E  a max b 1 f  b Ea  Eb d  Eb where d is the dimensionality.

Another famous formula is the Bruggeman's symmetric mixing rule, which is based on the structure of dilute spherical inclusions.

Ea  E Eb  E f a   fb   0 Ea  2E Eb  2E Here 2 is related to the depolarization factor of sphere (1/3). If the inclusion shape is ellipsoid or others, we should replace 2 with appropriate values.

There are also some other mixing rules, but there're much more complex. If you are interested, please take a look at: 3-5 Also you might find other references yourself.

1. Karkkainen, K. K., Sihvola, A. H. & Nikoskinen, K. I. Effective permittivity of mixtures: numerical validation by the FDTD method. Geoscience and Remote Sensing, IEEE Transactions on 38, 1303-1308 (2000). 2. Hashin, Z. & Shtrikman, S. A Variational Approach to the Theory of the Effective Magnetic Permeability of Multiphase Materials. Journal of Applied Physics 33, 3125-3131 (1962). 3. Milton, G. W. The Theory of Composites (eds. Ciarlet, P. G., Iserles, A., Kohn, R. V. & Wright, M. H.) (Cambridge University Press, 2002). 4. Walpole, L. J. On bounds for the overall elastic moduli of inhomogeneous systems--I. Journal of the Mechanics and Physics of Solids 14, 151-162 (1966). 5. Walpole, L. J. On bounds for the overall elastic moduli of inhomogeneous systems--II. Journal of the Mechanics and Physics of Solids 14, 289-301 (1966).