College of Engineering and Computer Science Mechanical Engineering Department Mechanical Engineering 390 Fluid Mechanics Spring 2008 Number: 11971 Instructor: Larry Caretto
Solution to Quiz Five –Control Volumes
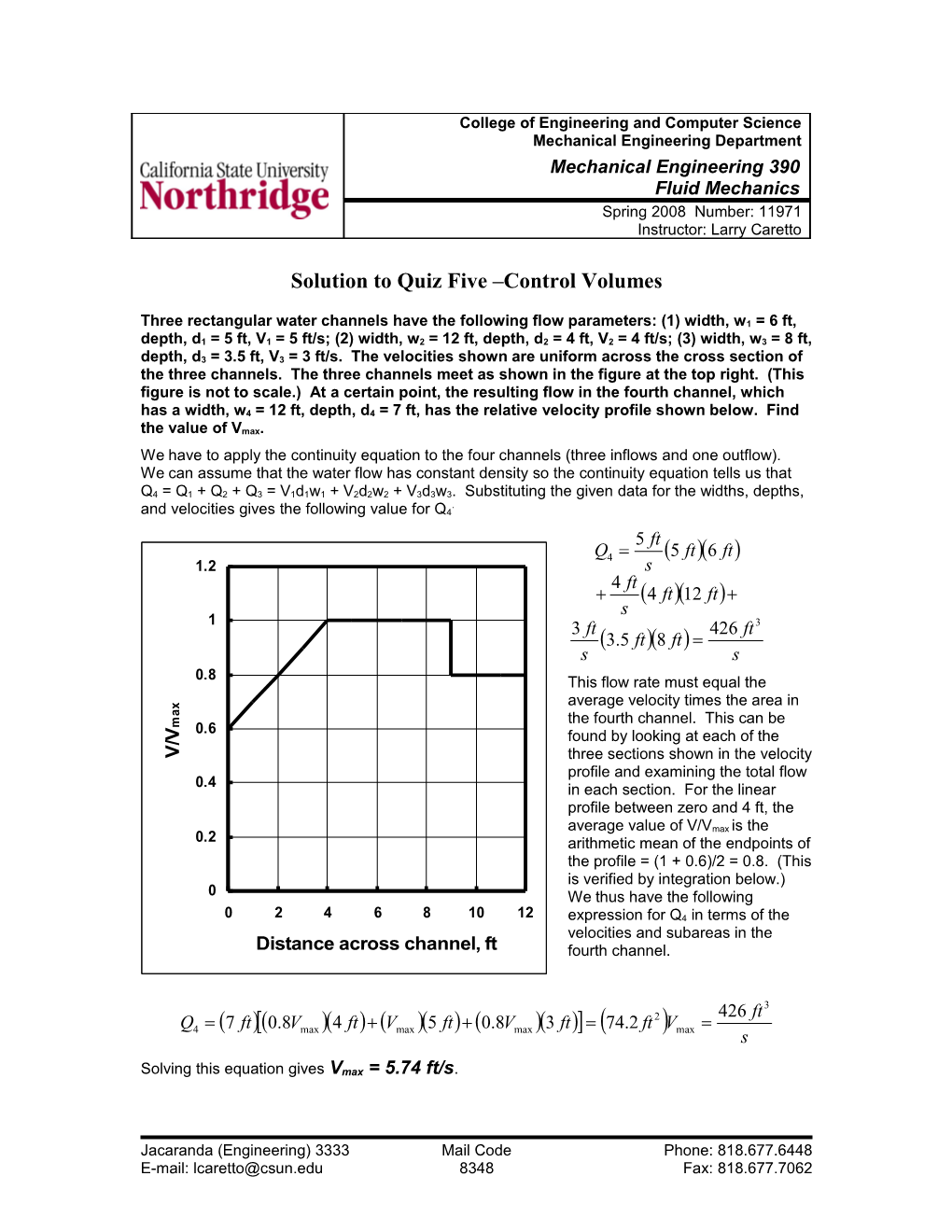
Three rectangular water channels have the following flow parameters: (1) width, w1 = 6 ft, depth, d1 = 5 ft, V1 = 5 ft/s; (2) width, w2 = 12 ft, depth, d2 = 4 ft, V2 = 4 ft/s; (3) width, w3 = 8 ft, depth, d3 = 3.5 ft, V3 = 3 ft/s. The velocities shown are uniform across the cross section of the three channels. The three channels meet as shown in the figure at the top right. (This figure is not to scale.) At a certain point, the resulting flow in the fourth channel, which has a width, w4 = 12 ft, depth, d4 = 7 ft, has the relative velocity profile shown below. Find the value of Vmax. We have to apply the continuity equation to the four channels (three inflows and one outflow). We can assume that the water flow has constant density so the continuity equation tells us that Q4 = Q1 + Q2 + Q3 = V1d1w1 + V2d2w2 + V3d3w3. Substituting the given data for the widths, depths, . and velocities gives the following value for Q4 5 ft Q4 5 ft6 ft 1.2 s 4 ft 4 ft12 ft s 1 3 ft 426 ft 3 3.5 ft8 ft s s 0.8 This flow rate must equal the average velocity times the area in x a the fourth channel. This can be m 0.6
V found by looking at each of the /
V three sections shown in the velocity profile and examining the total flow 0.4 in each section. For the linear profile between zero and 4 ft, the average value of V/Vmax is the 0.2 arithmetic mean of the endpoints of the profile = (1 + 0.6)/2 = 0.8. (This is verified by integration below.) 0 We thus have the following 0 2 4 6 8 10 12 expression for Q4 in terms of the velocities and subareas in the Distance across channel, ft fourth channel.
426 ft 3 Q 7 ft0.8V 4 ft V 5 ft 0.8V 3 ft 74.2 ft 2 V 4 max max max max s
Solving this equation gives Vmax = 5.74 ft/s.
Jacaranda (Engineering) 3333 Mail Code Phone: 818.677.6448 E-mail: [email protected] 8348 Fax: 818.677.7062 The statement above, that we could use the average value of a linear profile as the arithmetic mean of the endpoints, is verified by integration here. The equation for the straight line profile as a function of the distance across the channel, x, is found from the points that V/Vmax = 0.6 at x = 0 and V/Vmax = 1 at x = 4. The first point, at x = 0, gives us the intercept, b = 0.6, in the straight line equation V/Vmax = mx + b. The slope, m, is (V/Vmax)/x = (1 – 0.6)/(4 ft – 0 ft) = 0.1/ft. Thus the equation for our linear profile is V/Vmax = mx + b with m = (0.1/ft) and b = 0.6 (dimensionless). We find the average of the linear profile by integrating the profile over its entire length from x = 0 to x = 4 ft. 4 ft 4 ft V 1 V 1 dx mx bdx V 4 ft V 4 ft max 0 max 0 4 ft 1 mx2 1 m4 ft2 m4 ft bx b4 ft b 4 ft 2 4 ft 2 2 0 Substituting the values found previously that m = 0.1/ft and b = 0.6 gives the following result. V m4 ft 0.1ft 1 4 ft b 0.6 0.2 0.6 0.8 Vmax 2 2 This is the value that we computed previously by taking the mean of the endpoints.
Jacaranda (Engineering) 3333 Mail Code Phone: 818.677.6448 E-mail: [email protected] 8348 Fax: 818.677.7062